机器学习——朴素贝叶斯
目录
一、贝叶斯方法
背景知识
贝叶斯公式
二、朴素贝叶斯原理
判别模型和生成模型
1.朴素贝叶斯法是典型的生成学习方法
2.朴素贝叶斯法的基本假设是条件独立性
3.朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测
用于文本分类的朴素贝叶斯模型:
三、朴素贝叶斯案例
四、朴素贝叶斯代码实现
一、贝叶斯方法
背景知识
- 贝叶斯分类:贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。
- 先验概率:根据以往经验和分析得到的概率。我们用P(Y)来代表在没有训练数据前假设Y拥有的初始概率。
- 后验概率:根据已经发生的事件来分析得到的概率。以P(Y|X)代表假设X 成立的情下观察到Y数据的概率,因为它反映了在看到训练数据X后Y成立的置信度。
- 联合概率:联合概率是指在多元的概率分布中多个随机变量分别满足各自条件的概率。X与Y的联合概率表示为P(X,Y)、 P(XY) 或P(X∩Y) 。假设X和Y都服从正态分布,那么P(X<5,Y<0)就是一个联合概率,表示 X<5,Y<0两个条件同时成立的概率。表示两个事件共同发生的概率。
贝叶斯公式

朴素贝叶斯法是典型的生成学习方法。生成方法由训练数据学习联合概率分布 P(X,Y),然后求得后验概率分布P(Y|X)。
学习联合概率的方法:利用训练数据学习P(X|Y)的估计,与先验的P(Y)相乘,得到 P(X,Y)=P(X|Y) P(Y)
二、朴素贝叶斯原理
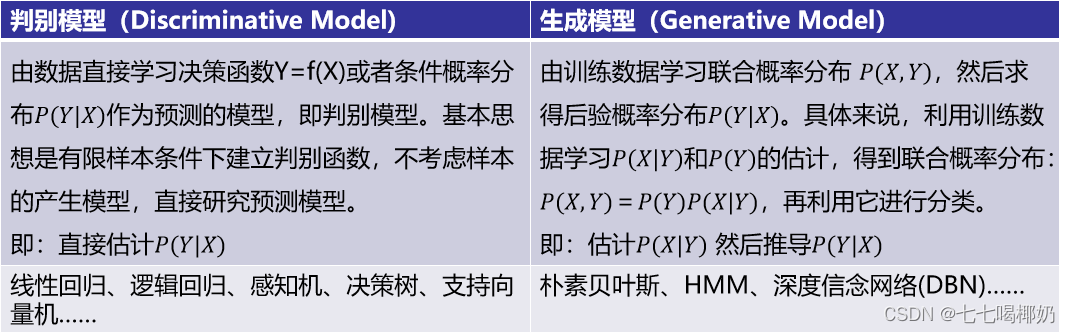
判别模型和生成模型
监督学习方法又分 生成方法(Generative approach)和判别方法(Discriminative approach)
所学到的模型分别称为 生成模型(Generative Model)和判别模型(Discriminative Model)。
1.朴素贝叶斯法是典型的生成学习方法
生成方法由训练数据学习联合概率分布 P(X,Y),然后求得后验概率分布P(Y|X)。具体来说,利用训练数据学习P(X|Y)和P(Y)的估计,得到联合概率分布:
概率估计方法可以是极大似然估计或贝叶斯估计。
2.朴素贝叶斯法的基本假设是条件独立性
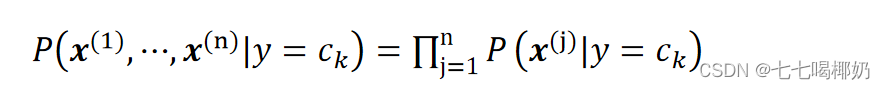
c_k代表类别,k代表类别序号。
这是一个较强的假设。由于这一假设,朴素贝叶斯法的学习与预测大为简化。因而朴素贝叶斯法高效,且易于实现。其缺点是分类的性能不一定很高。
3.朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测
我们要求的是P(Y|X),根据生成模型定义我们可以求P(X,Y)和P(Y)。 这个称作朴素贝叶斯假设条件独立,形式化表示为: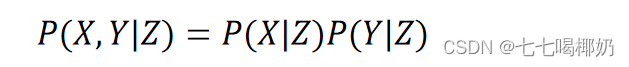 (给定Z的情况下,X、Y条件独立)
(给定Z的情况下,X、Y条件独立)
也可以表示为: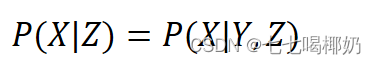
用于文本分类的朴素贝叶斯模型:
首先随机选定了邮件的类型y(垃圾邮件或普通邮件),然后一个人翻遍词典的所有词,依照概率p(x^(i)|y)随机决定一个词是否出现,出现标示为1,否则标示为0 。假设有50000个单词,那么这封邮件的概率可以表示为: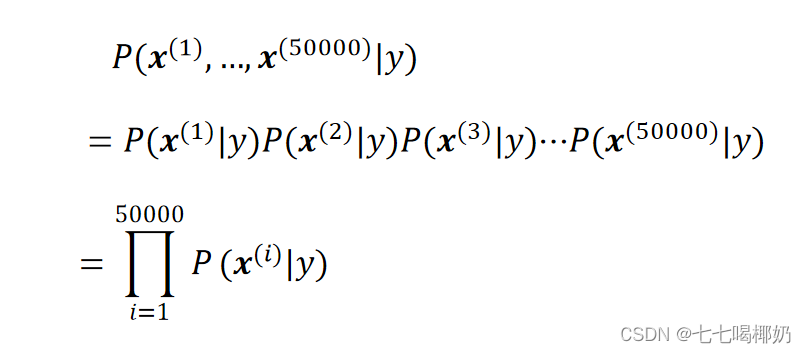
联合概率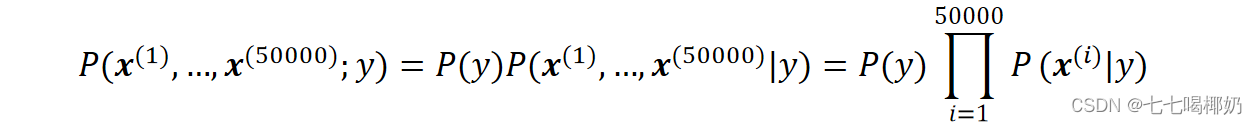 将输入x分到联合概率最大的类 y ̂ :
将输入x分到联合概率最大的类 y ̂ :
三、朴素贝叶斯案例
假设我们正在构建一个分类器,该分类器说明文本是否与运动(Sports)有关。我们的训练数据有5句话: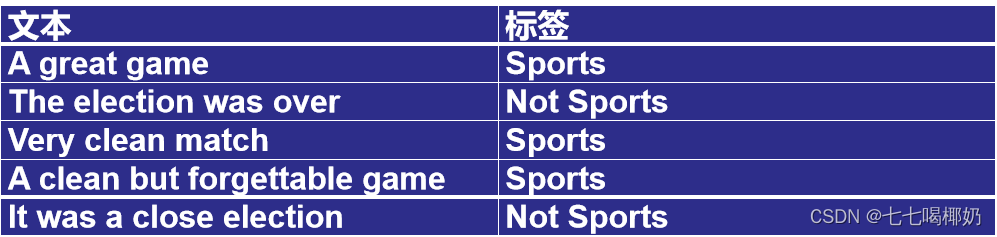
我们想要计算句子“A very close game”是 Sports 的概率以及它不是 Sports 的概率。
P( Sports | a very close game ) 即这个句子的类别是Sports的概率
特征:单词的频率
已知贝叶斯定理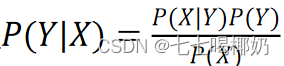 ,则:
,则:
由于我们只是试图找出哪个类别有更大的概率,可以舍弃除数,只是比较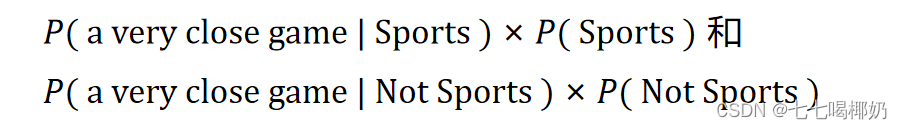 我们假设一个句子中的每个单词都与其他单词无关。
我们假设一个句子中的每个单词都与其他单词无关。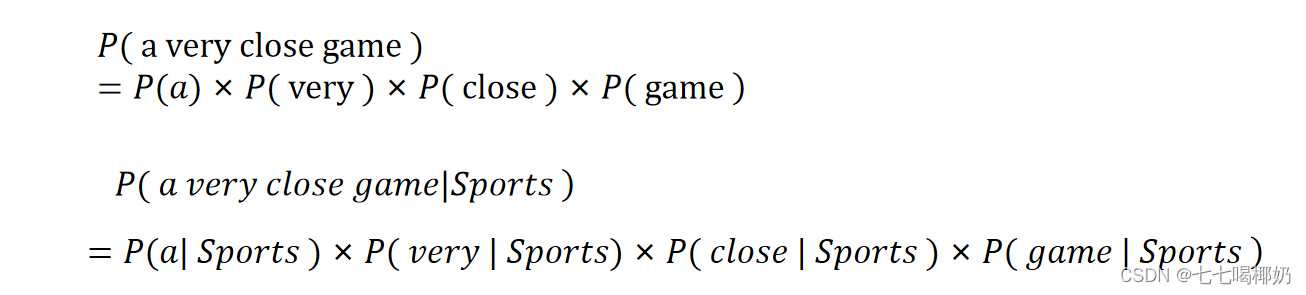
计算每个类别的先验概率:
对于训练集中的给定句子,P(Sports )的概率为⅗。P(Not Sports )是⅖。
然后,再计算P(game│Sports)就是“game”有多少次出现在Sports的样本,然后除以sports为标签的文本的单词总数(3+3+5=11)。
因此,P(game│Sports)=2/11。
“close”不会出现在任何sports样本中!那就是说P(close│Sports)=0。
通过使用一种称为拉普拉斯平滑的方法:我们为每个计数加1,因此它永远不会为零。为了平衡这一点,我们将可能单词的数量添加到除数中,因此计算结果永远不会大于1(且保证了最终和为1的概率性质)。
在这里的情况下,可能单词是['a', 'great', 'very', 'over', 'it', 'but', 'game', 'election', 'clean', 'close', 'the', 'was', 'forgettable', 'match']。
由于可能的单词数是14,因此应用平滑处理可以得到 P( game | sports )=(2+1)/(11+14)
拉普拉斯平滑是一种用于平滑分类数据的技术。引入拉普拉斯平滑法来解决零概率问题,通过应用此方法,先验概率和条件概率可以写为
其中K表示类别数量,A表示a_j中不同值的数量,通常λ=1 加入拉普拉斯平滑之后,避免了出现概率为0的情况,又保证了每个值都在0到1的范围内,又保证了最终和为1的概率性质。


四、朴素贝叶斯代码实现
最常用的GaussianNB是高斯贝叶斯分类器。它假设特征的条件概率分布满足高斯分布:


其他贝叶斯分类器:
- MultinomialNB是多项式贝叶斯分类器,它假设特征的条件概率分布满足多项式分布;
- BernoulliNB是伯努利贝叶斯分类器。它假设特征的条件概率分布满足二项分布。
GaussianNB是高斯朴素贝叶斯分类器的scikit-learn实现。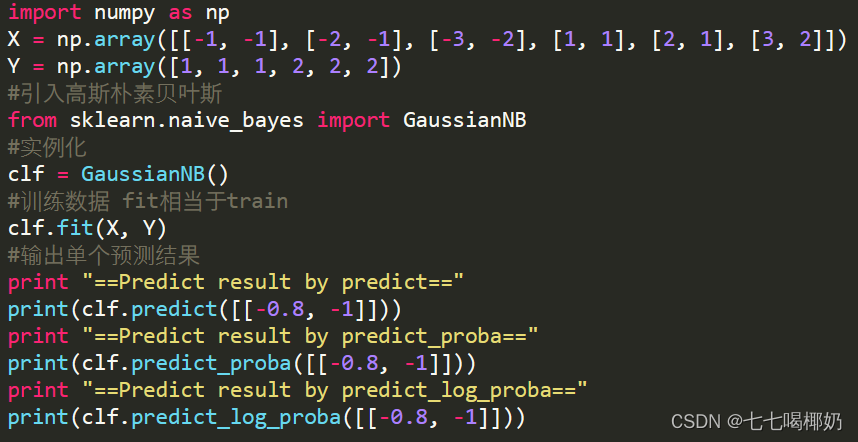
GaussianNB是高斯朴素贝叶斯分类器的Numpy实现。 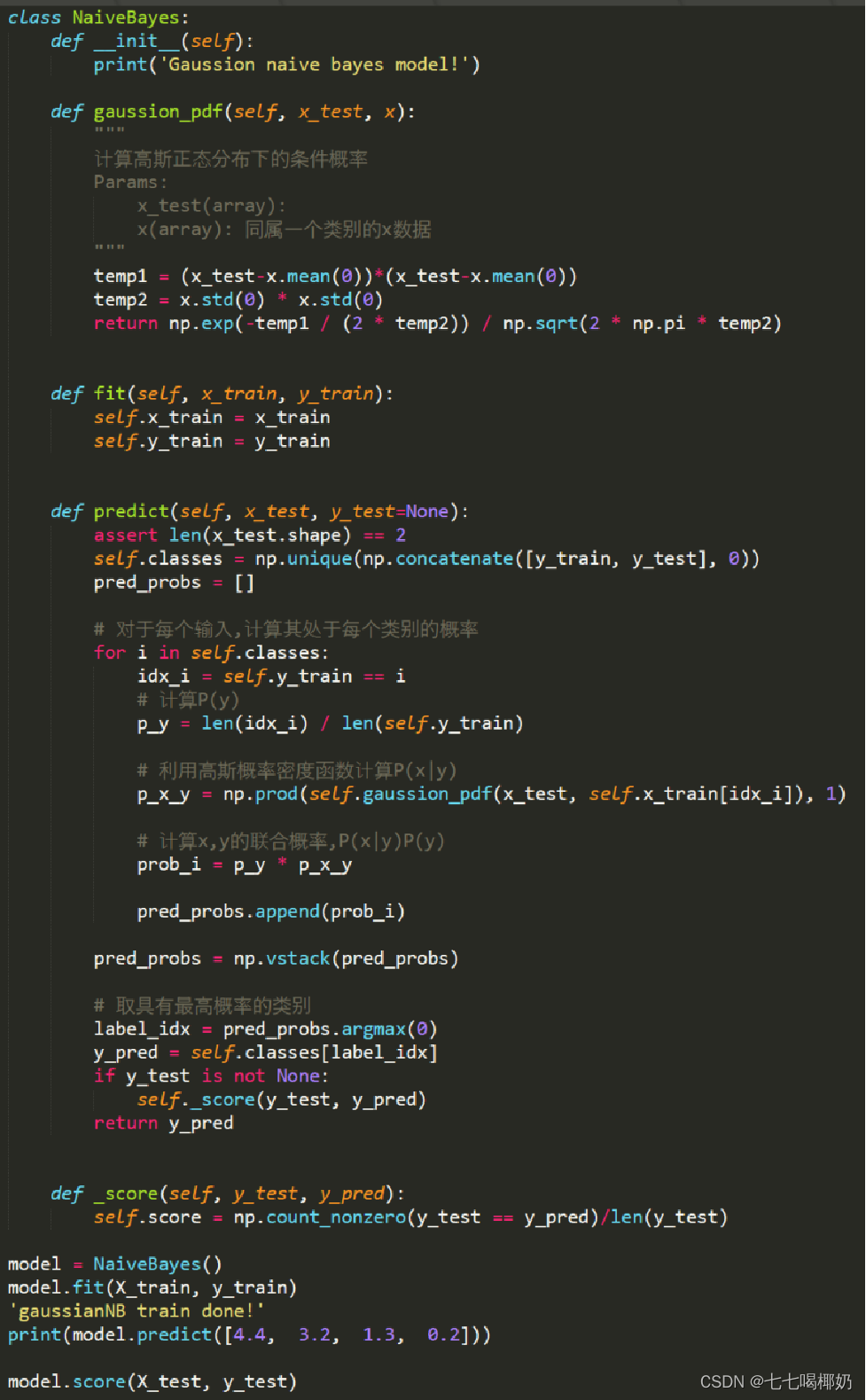
相关文章:

机器学习——朴素贝叶斯
目录 一、贝叶斯方法 背景知识 贝叶斯公式 二、朴素贝叶斯原理 判别模型和生成模型 1.朴素贝叶斯法是典型的生成学习方法 2.朴素贝叶斯法的基本假设是条件独立性 3.朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测 用于文…...

【PTE-day07 文件上传2】
1、常见的绕过方式 (1)畸形后缀名绕过 .php、.pht、.php3、.php4、.php5、.php2、.phtml、.pHp、.html、.Htm......(2)双写过滤字符绕过 (3).htaccess文件绕过 <FilesMatch "jpg"> SetHandler application/x-httpd-php...
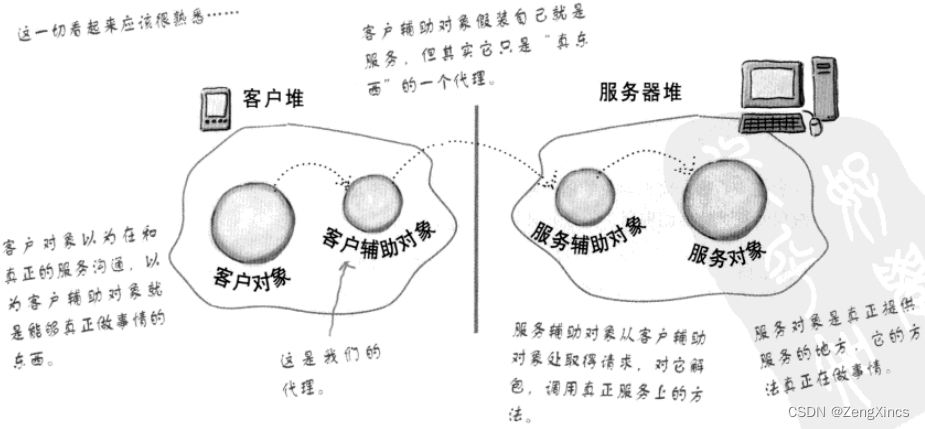
设计模式之十一:代理模式
代理可以控制和管理访问。 RMI提供了客户辅助对象和服务辅助对象,为客户辅助对象创建和服务对象相同的方法。RMI的好处在于你不必亲自写任何网络或I/O代码。客户程序调用远程方法就和运行在客户自己本地JVM对对象进行正常方法调用一样。 步骤一:制作远程…...

在spring boot中调用第三方接口时重试问题
文章目录 前言 spring-retry对第三方接口做重试,和处理操作 一、引入依赖 <!--重试请求的注解依赖--><dependency><groupId>org.springframework.retry</groupId><artifactId>spring-retry</artifactId></dependency>&l…...

记录一次多数据源配置失效的情况
说明:在一些复杂的业务情景,比如我们需要在一个订单审核通过后,在将数据库状态修改的同时,将订单与订单详细这两条数据写入到另一个数据库中。我们就可以通过在配置文件中,配置多数据源,然后通过在Mapper的…...

EasyExcel导出替换列中的变量
基于easyexcel2.0版本 easyexcel官网:https://easyexcel.opensource.alibaba.com/docs/2.x/quickstart/write 测试代码地址:https://gitee.com/wangtianwen1996/cento-practice/blob/master/src/test/java/com/xiaobai/easyexcel/DynamicHeadTest.java …...

机器人规划算法——将多边形障碍物离散到地图像素点上?
问题一:如何判断一个点是否在多边形区域内? 方法1:向量叉乘判别法 设多边形的顶点依次为A1,A2…An,要判断的点为P,那么分别计算向量PA1叉乘向量PA2,向量PA2叉乘向量PA3,…ÿ…...
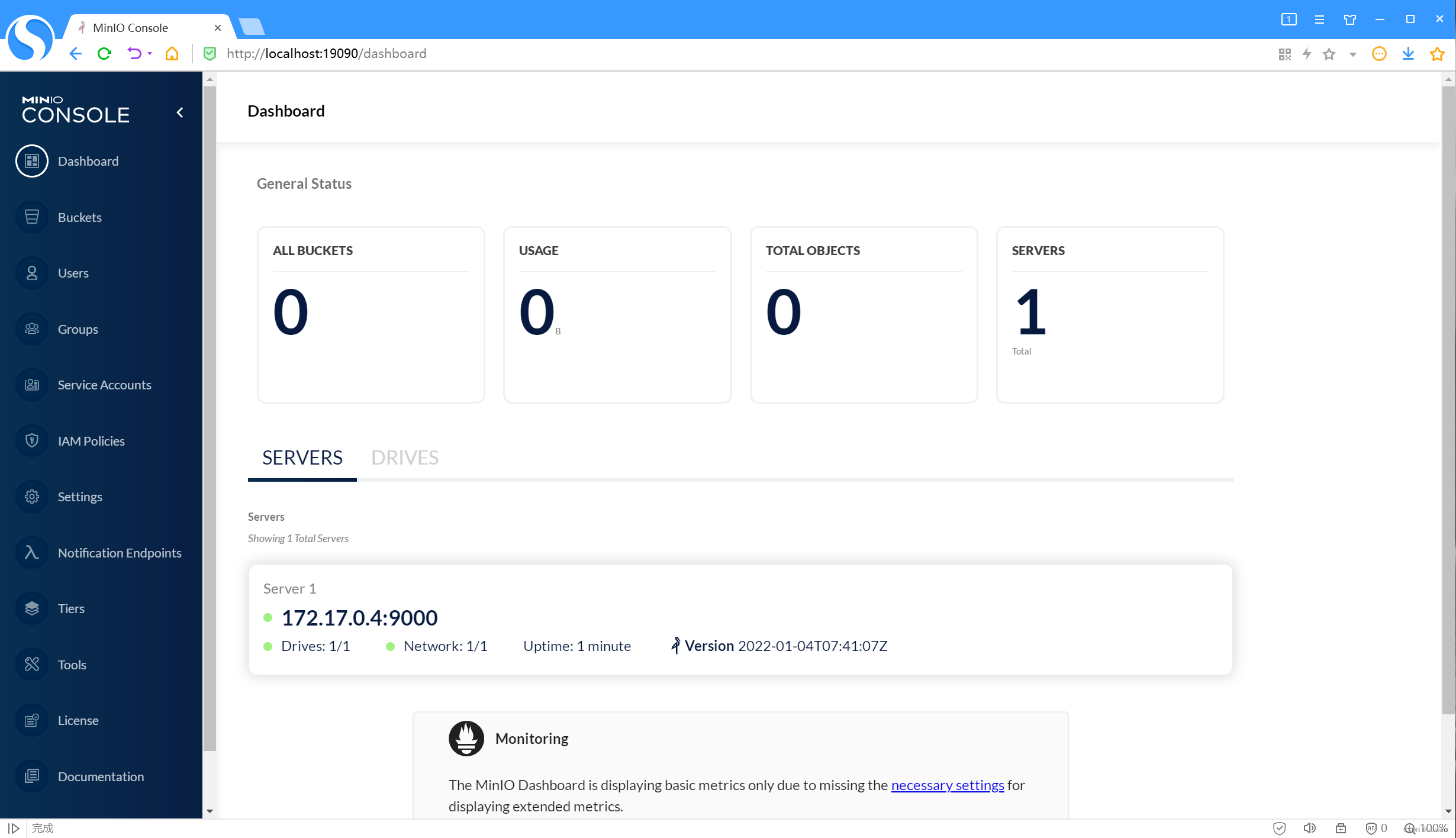
windows11使用docker部署安装minio
时间 2023-11-08 windows11使用docker部署安装minio 目录 1.docker 下载镜像2.docker安装镜像3.访问控制台4.安装问题解决5.使用教程 1.docker 下载镜像 调整镜像源到国内,否则会很慢 docker pull minio/minio2.docker安装镜像 设置用户名和密码时需要注意&…...

【JavaEESpring】Spring Web MVC⼊⻔
Spring Web MVC 1. 什么是 Spring Web MVC1.1 什么是 MVC ?1.2 是什么 Spring MVC? 2. 学习 Spring MVC2.1 建立连接2.2 请求2.3 响应 3. 相关代码链接 1. 什么是 Spring Web MVC 官⽅对于 Spring MVC 的描述是这样的: 1.1 什么是 MVC ? MVC 是 Model View C…...
flutter逆向 ACTF native app
前言 算了一下好长时间没打过CTF了,前两天看到ACTF逆向有道flutter逆向题就过来玩玩啦,花了一个下午做完了.说来也巧,我给DASCTF十月赛出的逆向题其中一道也是flutter,不过那题我难度降的相当之低啦,不知道有多少人做出来了呢~ 还原函数名 flutter逆向的一大难点就是不知道l…...
【Redis】set 集合
上一篇:list 列表 https://blog.csdn.net/m0_67930426/article/details/134364315?spm1001.2014.3001.5501 目录 Sadd Smembers Sismember Scard Srem 编辑Srandomember Spop Smove 集合类 Sdiff Sinter Sunion 官网 https://redis.io/commands/?…...
【算法与设计模式】
一、数据结构与算法 1、算法性能评估 时间复杂度、空间复杂度 2、数据结构 数组与列表 队列 堆栈 链表 二叉树 多叉树 递归算法 二、设计模式 1、单例 (1)GIL:线程互斥锁。保证同一时刻只有一个线程在进行。 (2)…...

Javaweb之javascript的小案例的详细解析
1.5.4 案例 1.5.4.1 需求说明 鲁迅说的好,光说不练假把式,光练不说傻把式。所以接下来我们需要通过案例来加强对于上述DOM知识的掌握。需求如下3个: 点亮灯泡 将所有的div标签的标签体内容后面加上:very good 使所有的复选框呈现被选中的…...
Vant 移动端UI 组件自动引入
Vue项目中安装Vant # Vue 3 项目,安装最新版 Vant npm i vant 组件按需引入配置 Vant按需引入- - -安装:unplugin-vue-components 插件 unplugin-vue-components 插件可以在Vue文件中自动引入组件(包括项目自身的组件和各种组件库中的组件&…...
敏捷开发是什么?敏捷开发流程是怎么样的?
1. 什么是敏捷开发? 敏捷开发是一种迭代、增量式的软件开发方法,旨在通过灵活、协作和快速响应变化的方式,提高开发团队的效率和产品的质量。相较于传统的瀑布式开发模型,敏捷开发更加注重用户需求的响应和团队协作࿰…...
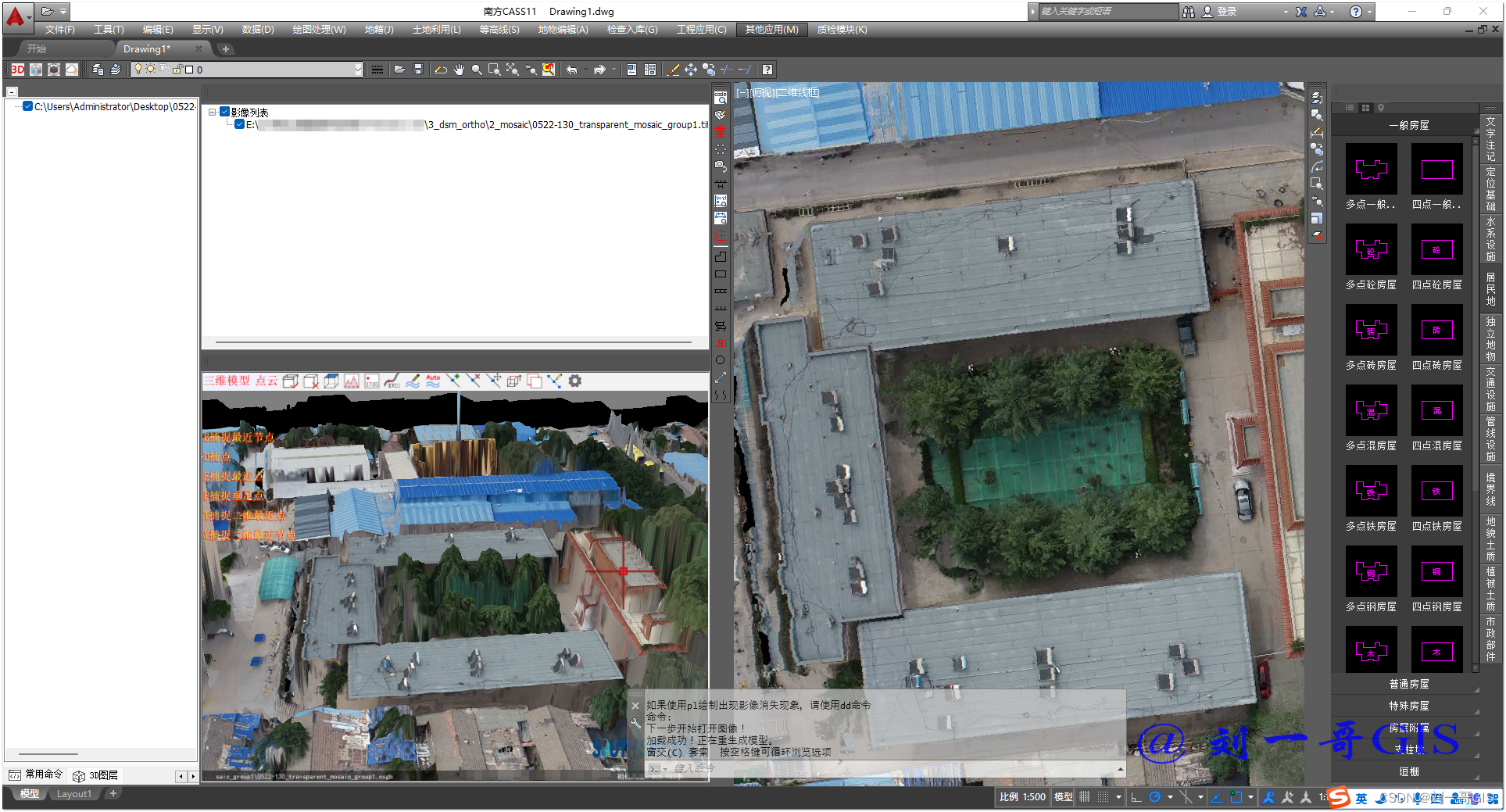
【CASS精品教程】cass3d 11.0加载超大影像、三维模型、点云数据
CAD2016+CASS11.0(内置3d)下载与安装: 【CASS精品教程】CAD2016+CASS11.0安装教程(附CASS11.0安装包下载)https://geostorm.blog.csdn.net/article/details/132392530 一、cass11.0 3d支持的数据 cass11.0中的3d模块增加了多种数据的支持,主要有: 1. 三维模型 点击…...
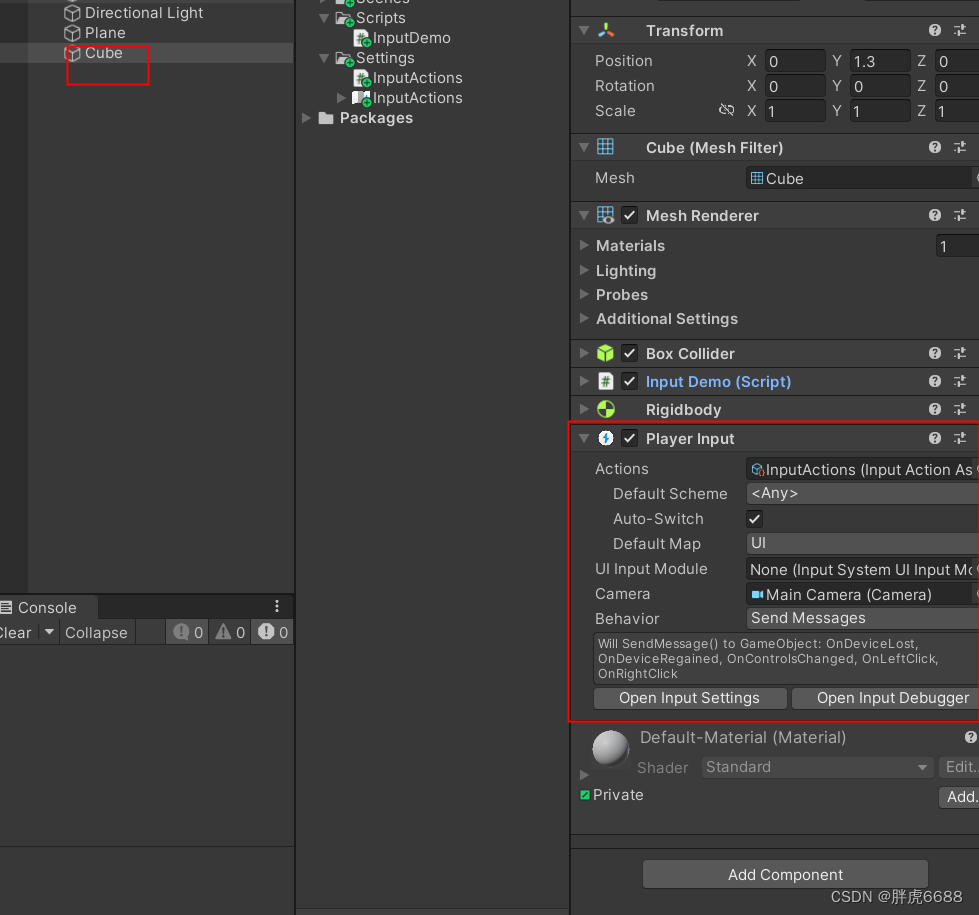
Unity Input System最简单使用
开始学的是 Input Manager 比较好理解,Input System却不好理解,教程也找了很多,感觉都讲的不清楚,我这里做一个最简单的用 Input System 添加鼠标左键和右键的效果。 1. 安装 Input System 包 首先这个功能不是内置的࿰…...
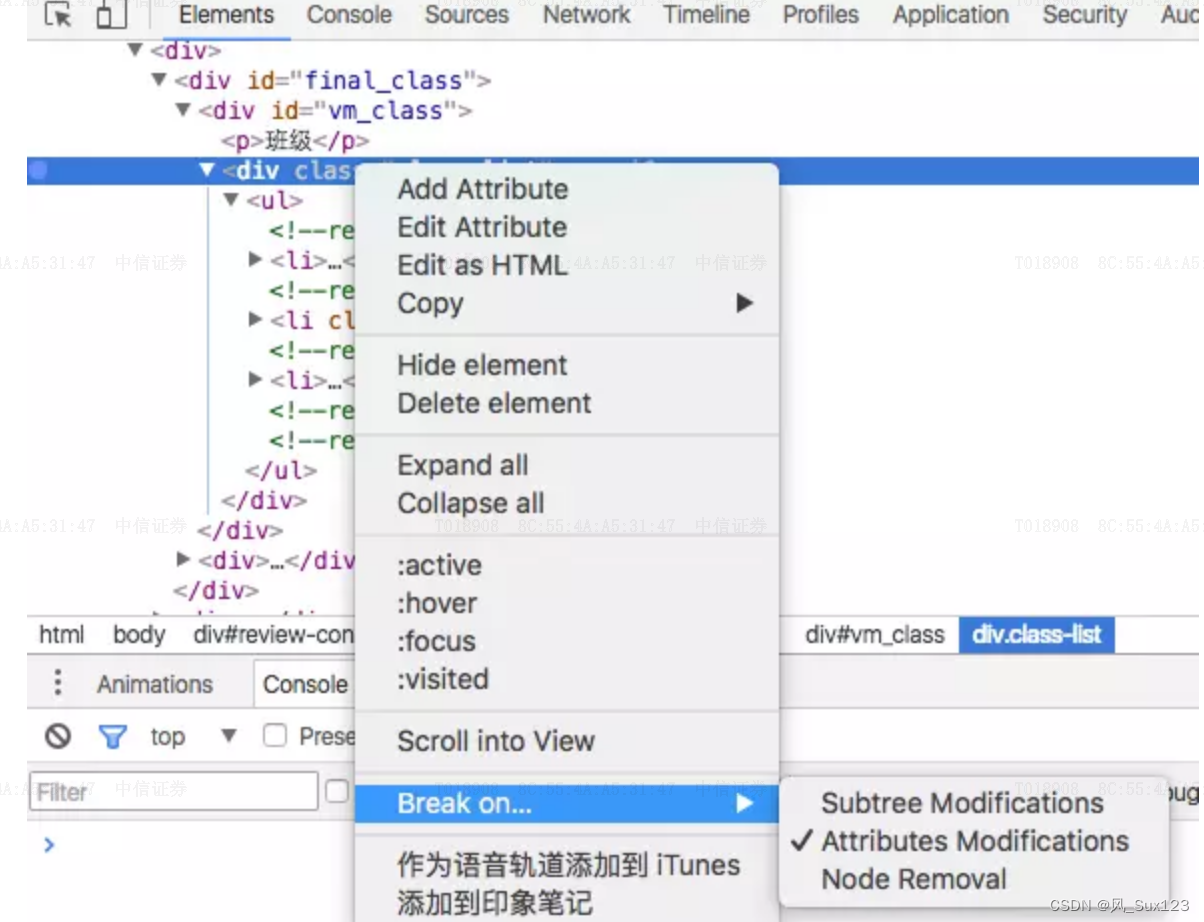
3.前端调式(断点调式)
1. Elements 先来看这张图最上头的一行是一个功能菜单,每一个菜单都有它相应的功能和使用方法,依次从左往右来看 箭头按钮 用于在页面选择一个元素来审查和查看它的相关信息,当我们在Elements这个按钮页面下点击某个Dom元素时,箭…...
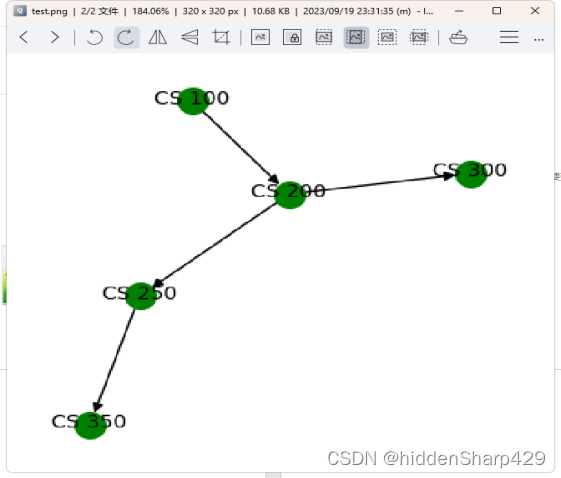
拓扑排序软件设计——ToplogicalSort_app(含有源码、需求分析、可行性分析、概要设计、用户使用手册)
拓扑排序软件设计 前言1. 需求分析2. 可行性分析2.1 简介2.2 技术可行性分析2.2.1 技术实现方案2.2.2 开发人员技能要求2.2.3 可行性 2.3 操作可行性分析2.4 结论 3. 项目报告3.1 修订历史记录3.2 软硬件环境3.3 需求分析3.4 详细设计3.4.1 类设计3.4.2 核心流程描述3.4.3 核心…...

ESP32网络开发实例-将数据保存到InfluxDB时序数据库
将数据保存到InfluxDB时序数据库 文章目录 将数据保存到InfluxDB时序数据库1、InfluxDB介绍与安装3、软件准备4、硬件准备5、代码实现6、InfluxDB数据可视化在本文中,将介绍 InfluxDB 以及如何将其与 ESP32 开发板一起使用。 我们将向展示如何创建数据库桶并将 ESP32 数据发送…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...