MATLAB的编程与应用,匿名函数、嵌套函数、蒙特卡洛法的掌握与使用

目录
1.匿名函数
1.1.匿名函数的定义与分类
1.2.匿名函数在积分和优化中应用
2.嵌套函数
2.1.嵌套函数的定义与分类
2.2.嵌套函数彼此调用关系
2.3.嵌套函数在积分和微分中应用
3.微分和积分
4.蒙特卡洛法
4.1.圆周率的模拟
4.2.计算N重积分(均匀分布)
4.3.计算N重积分(等序列分布)
1.匿名函数
1.1.匿名函数的定义与分类
匿名函数(Anonymous function)
定义:f = @(X)expr
x为指定的函数的自变量,Expr为具体的函数表达式。
f = @(x) x.^2; ff = f(1:10) ff = 1 4 9 16 25 36 49 64 81 100 g = @(x,y) x.^2 + y.^2; gg = g(1:4,2:5) gg = 5 13 25 41
单变量匿名函数
定义:f =@(x) expr
-
x为指定函数的自变量,Expr为具体的函数表达式
f = @(x) x.^2
-
含有参数的匿名函数,当参数已知的时候
a = 10, b = 20; f = @(x) a*x.^2+b; f(1:5) ans = 30 60 110 180 270
-
多变量匿名函数
g = @(x,y) x.^2+y.^2; % 含有参数的匿名函数,当参数已知的时候 a = 1,b = 2; f = @(x,y) a*x.^2+b*y; f(1:5,2:6) ans = 5 10 17 26 37
多重匿名函数
只有一个@符号的为单重匿名函数;有多个@符号的为二重、多重匿名函数,在参数传递方面非常方便。例:简单的二重匿名函数
f = @(a,b) @(x) a*x.^2+b*x+2; f(2,3) ans = @(x) a*x.^2+b*x+2 ans(3) ans = 29
这个段代码有一点问题,运行结果是17
改成下面的代码才是正确的输出:29
多重匿名函数
f = @(a) a(b,c) @(x) a*x.^2+b*x+c;
匿名函数在解方程中的应用
匿名函数可以非常方便地表达所求方程,并提供fzero等函数调用。例1:求下列方程的根
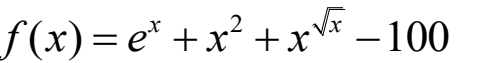
f = @(x) exp(x) + x.^2 + x.^(sqrt(x)) - 100; x0 = fzero(f,3) x0 =4.1635 f(x0) ans =2.8422e-14
匿名函数在解方程中的应用
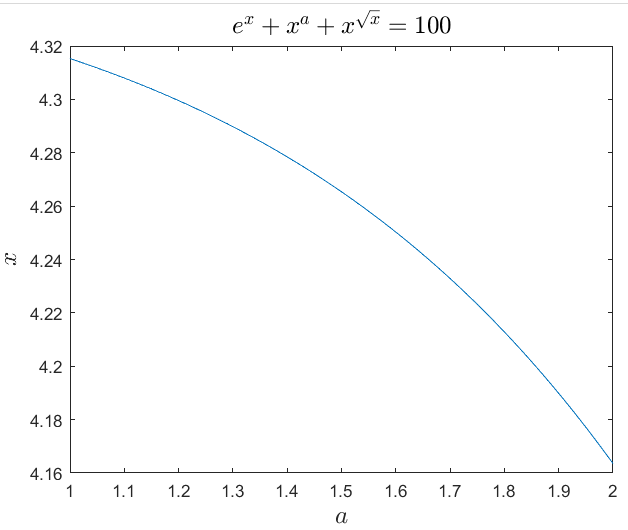
不同参数一一求解对应方程的根时,调用arrayfun函数。例1续:a = [0, 0.01, 0.02, ...., 2]求下列方程相应的根,画出a和相应的x的图像。
f = @(a) @(x) exp(x) + x^a + x^(sqrt(x)) - 100;
aa = 1:0.01:2;
y = arrayfun(@(a) fzero(f(a), 4), aa);
%运用arrayfun函数批量处理
plot(aa, y)
xlabel('$a$','interpreter','latex','fontsize',15)
ylabel('$x$','interpreter','latex','fontsize',15)
title('$e^x+x^a+x^{\sqrt{x}}=100$','interpreter','latex','fontsize',15)
匿名函数在表示隐函数方面的应用
隐函数一般无数学上的显式表示,运用matlab,对自变量x运用数值解给出因变量y。
例1:显式表示下列y关于x的隐函数
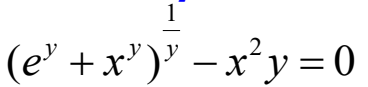
y = @(x) fzero(@(y)(exp(y)+x^y)^(1/y)-x^2*y,1); y(1) ans =2.7779
希望接受向量形式的输入,结合arrayfun函数
y = @(x) arrayfun(@(xx)fzero(@(y)(exp(y)+xx^y)^(1/y)-xx^2*y,1),x); y(1:5) ans =2.7779 1.1055 0.7759 0.6284 0.5425
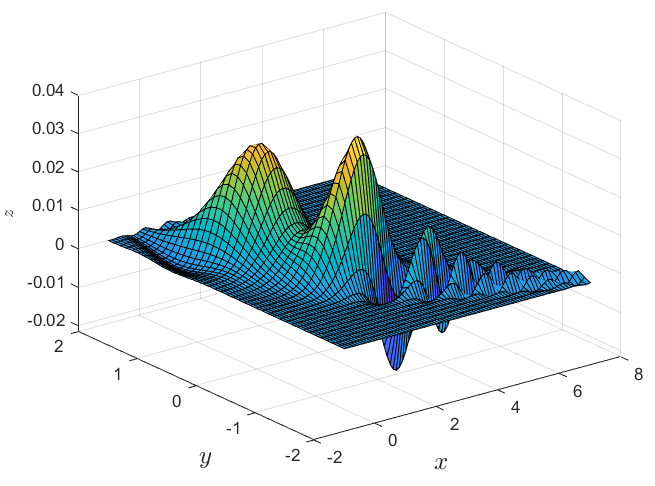
例2:显式表示Z关于x,y的函数
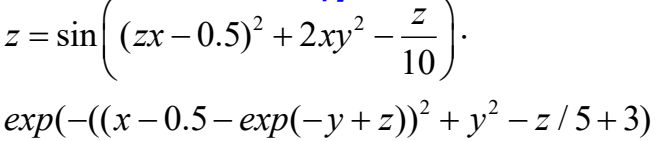
接受向量形式的输入,结合arrayfun、fzero函数
z = @(x,y) fzero(@(z)z-sin((z*x-0.5*)^2+2*x*y^2-z/10)*exp(-((x-0.5-exp(-y+z))^2+y^2-z/5+3)),rand);
[X,Y] = meshgrid(-1:0.1:7,-2:0.1:2);
Z = arrayfun(@(x,y) z(x,y), X, Y)
surf(X, Y, Z)
%坐标轴和函数标题
xlabel('$x$','interpreter','latex','fontsize',15)
ylabel('$y$','interpreter','latex','fontsize',15)
zlabel('$z$','interpreter','latex','fontszie',15)
title('$z=\sin((zs-0.5)^2+zxy^2-z/10)\exp(-((x-0.5-\exp(-y+z))^2+y^2-z/5+3))$','interpreter','latex','fontsize',15)
1.2.匿名函数在积分和优化中应用
匿名函数在求积分区域中的应用
在对称区间积分,求积分区间[-t,t],使得
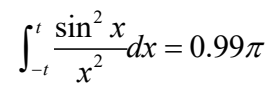
z=fzero(@(u) 0.99*pi/2-quadl(@(x)sin(x).^2./x.^2, 0, u), 1) z =32.3138
匿名函数在数值积分中的应用
求下列函数的三阶导数在区间[0,1]上的图像
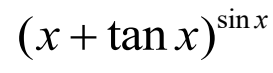
syms x;
f=(x+tan(x))^sin(x);
c=diff(f,3);
t=0:0.01:1;
f3=eval(['@(x)' vectorize(c)]);
plot(t,f3(t))
xlabel('x')
ylabel('y')
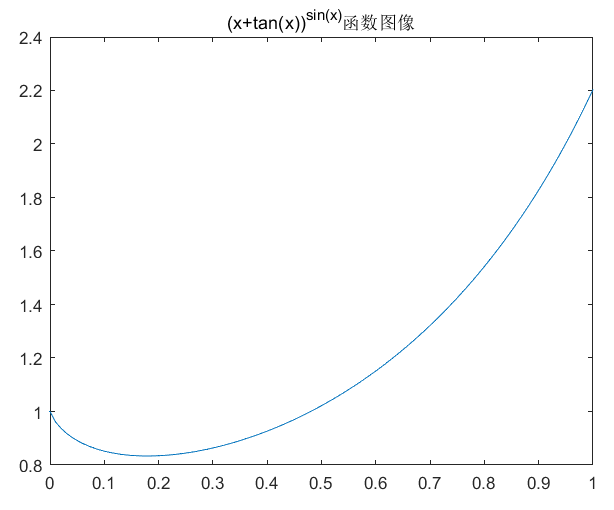
title('(x+tan(x))^{sin(x)}三阶导数图像')
三节导函数的图像
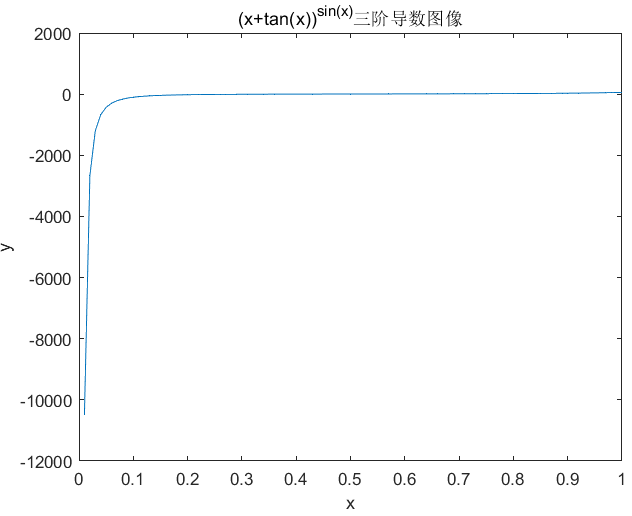
x=0:0.01:1;
y=(x+tan(x)).^sin(x);
plot(x,y)
title('(x+tan(x))^{sin(x)}函数图像')
函数图像
2.嵌套函数
2.1.嵌套函数的定义与分类
嵌套函数nested-function
嵌套函数的优点
-
可以方便解决变量共享问题;
-
复杂的表达式中涉及的参数传递;
-
编写GUI(图形用户界面)时,参数传递问题。
嵌套在函数体内部的函数,嵌套函数可以方便的实现变量共享,可以出现在函数体内部任意位置,除if/else,while,switch等结构语句中。嵌套函数在尾末必须加上end。
例1:嵌套函数简单应用(内外变量共享)
function r = MyTestNestedFun(input) a = 5; c = sin(input)+tan(input); function y = nestedfun(b) y = a*c+b; end r = nestedfun(5); end
例2:嵌套函数的变量作用域(内部调用外部)
function r = NestedFunctionVarScopeDemo(a) b = a+1;function Nested1c = b+1;function Nested11d = c+a;endNested11;end Nested1
例3:嵌套函数的变量作用域2(未调用时不运行)
function r = NestedFunctionVarScopeDemo2(a) b = a+1;function Nested1c = b+1function Nested11d = c+a;endend Nested1 e = c1 r = d; end
例4:嵌套函数的变量作用域3(无嵌套关系,不能共享)
function r = NestedFunctionVarScopeDemo3(a) b = a+1;function Nested1c = b+1;c1 = 10;Nested2;c2 = d^2; %这一步有问题end Nested1 r = c2 end
2.2.嵌套函数彼此调用关系
例5:父函数与子函数(父调用子,不能调用孙)
function r = NestedFunctionCallDemo1(a) b = a+1;function c1 = Nested1(x)c = b+1;c1 = 10+c*x;function d = Nested11d = c+a;endend c1 = Nested1(1); r = Nested11; end
例6:父函数与子函数(子调用父,孙调用爷)
function NestedFunctionCallDemo2(flag)
switch flagcase 1disp('flag = 1')return;case 2disp('flag = 2')return;case 3disp('flag = 3')returnotherwisedisp(['flag = ', num2str(flag)]);returnend
function NestedFunctionCallDemo2(flag)% 续function NestedFun1NestedFunctionCallDemo2(1);%子调用父;NestedFun2function NestedFun2NestedFunctionCallDemo2(3);%孙调用爷;endend
end
例7:父函数与子函数(子调用叔父)
function NestedFunctionCallDemo3 Nested1(5)function Nested1(x)disp(['Nested1执行,输入:', num2str(x)])Nested2(6)function Nested11(xx)disp(['Nested11执行,输入:',num2str(xx)]);endendfunction Nested2(y)disp(['Nested2执行,输入:',num2str(y)])function Nested22(yy)disp(['Nested22执行,输入:',num2str(yy)]);endend end
例8:父函数与子函数(孙调用大爷,不能用堂伯堂哥)
function NestedFunctionCallDemo4 Nested1(5)function Nested1(x)disp(['Nested1执行,输入:', num2str(x)])Nested11(6)function Nested11(xx)disp(['Nested11执行,输入:',num2str(xx)]);Nested2(pi)Nested22(10);endendfunction Nested2(y)disp(['Nested2执行,输入:', num2str(y)])Nested22(pi*pi)function Nested22(yy)disp(['Nested22执行,输入:',num2str(yy)]);endend end
父函数与子函数:
嵌套:父亲,儿子,孙子
不同嵌套:亲属关系
父子互助,不能求孙
子可求父、伯、大爷、爷,不能求侄儿
2.3.嵌套函数在积分和微分中应用
例1:求积分,已知a,e和l,求\beta_0?

function sol = example541(a,e,l)function fun(beta)f =a.*(1-e.^2)./(1-e.^2.*sin(beta).^2).^(3/2);endfunction g = fun(beta0)g = quadl(@fun1,0,beta0)-1;endsol = fzero(@fun2,3); end sol = example541(20,0.6,6)
例2:
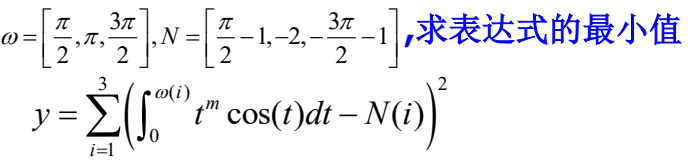
function m = Findm w = [pi/2, pi, pi*1.5] N = [pi/2-1, -2, -1.5*pi-1]; function y = ObjecFun(m)y = (quadl(@(t) t.^m.*cos(t), 0, w(1))^2 + (quadl(@(t).^m.*cos(t), 0, w(2))^2 + (quadl(@(t).^m.*cos(t), 0, w(3))^2; end m = fminbnd(@ObjecFun, 0, 2); end % 第二段代码 function m = Findm w = [pi/2, pi, pi*1.5]; N = [pi/2-1, -2, -1.5*pi-1]; function y = ObjecFun(m) s = @(w)arrayfun(@(ww) quadl(@(t) t.^m.*cos(t), t, ww), w); y = sum((s(w)-N).^2); end m = fminbnd(@ ObjecFun, 0, 2); end
例3:求微分方程在[0, 5]范围的解,a为参数
![]()
function example545(a)
tspan = [0,5]; % 变量求解区间
y0 = [1,0]; % 初值
[t,y] = ode45(@tfys, tspan, y0); % 调用ode45求解方程
figure;
plot(t, y(:,1),'k'); %画函数y(t)的曲线
hold on;
plot(t,(:,2), 'k:'); %画函数y(t)导数的曲线
set(gca,'fontsize',12); % 设置当前坐标轴字体大小
xlabel('\itt','fontsize',16); %标注x轴
ylabel('\ity','fontsize',16); %标注y轴
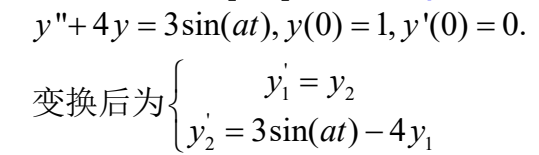
function example545(a) %嵌套函数定义微分方程组function dy = tfys(t,y)dy(1,1) = y(2); %对应于例子中方程组第一个方程dy(2,1) = 3*sin(a*t)-4*y(1);%对应于例子中方程组第二个方程end end
3.微分和积分
敬请期待
4.蒙特卡洛法
4.1.圆周率的模拟
例1:蒲丰投针问题
18世纪,蒲丰提出以下问题:设我们有一个以平行且等距木纹铺成的地板(如图),现在随意抛一支长度比木纹之间距离 小的针,求针和其中一条木纹相交的概率。并以此概率,布丰提出的一种计算圆周率的方法——随机投针法。这就是蒲丰投针问题(又译“布丰投针问题”)
证明:由于向桌面投针是随机的,所以用二维随机变量(X,Y)来确定它在桌上的具体位置。设X表示针的中点到平行线的的距离,Y表示针与平行线的夹角,如果x<l/2sin(y)时,针与直线相交。
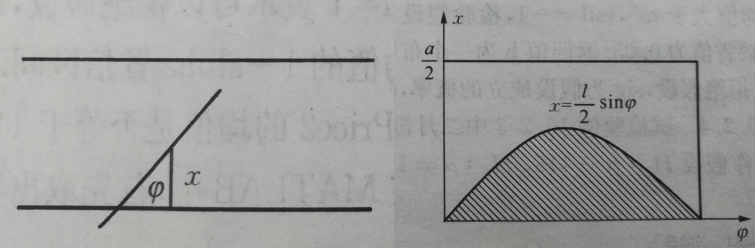
并且X在服从均匀分布,Y在服从均匀分布,XY相互独立,由此可以写出(X,Y)的概率密度函数
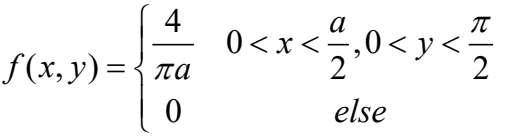
因此所求概率
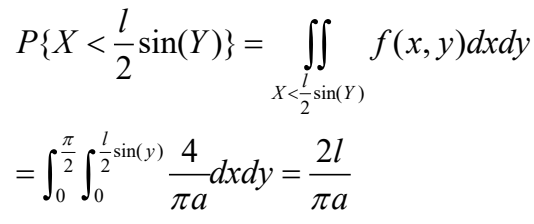
Monte Carlo方法是计算机模拟的基础,它的名字来源于世界著名的赌城——摩纳哥的蒙特卡洛, 其历史起源于 1777 年法国科学家蒲丰提出的一种计算圆周π 的方法——随机投针法,即著名的蒲丰投针问题。
Monte Carlo方法的基本思想是首先建立一个概率模型,使所求问题的解正好是该模型的参数或其他有关的特征量. 然后通过模拟一统计试验, 即多次随机抽样试验 (确定 m和 n) ,统计出某事件发生的百分比。只要试验次数很大,该百分比便近似于事件发生的概率.这实际上就是概率的统计定义。利用建立的概率模型,求出要估计的参数。蒙特卡洛方法属于试验数学的一个分支。
MATLAB语言编程实现:1)
l = 1; a = 2;n = 10000;m = 0; for k = l : n x = unifrnd(0, a/2); y = unifrnd(0, pi/2);if x < l/2*sin(y)m=m+1;end end p=m/n;pi_m=1/p pi_m=3.2584
2)
l=1;a=2;n=10000;m=0; x=unifrnd(0,a/2,1,n); y=unifrnd(0,pi/2,1,n); [gs,wz]=find(x<l/2*sin(y)); m=sum(gs); p=m/n;pi_m=1/p pi_m=3.1636
4.2.计算N重积分(均匀分布)
原理:用蒙特卡洛法计算N重积分积分:设D为n维空间Rn的一个区域,f(x)∈D Rn→R,区域D上的n 重积分用下式表示:
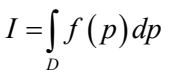
可以认为 I=(区域D的测度) X (函数f的期望)。基本的蒙特卡洛法就是找一个超立方体(测度已知,为Mc)包含区域D,在D内随机生成n(n一般足够大)个均匀分布的点,统计落入区域D的点,假设有m个。
则区域D的测度
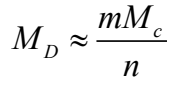
函数f的期望
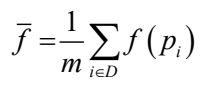
积分为

例1:用蒙特卡洛法计算积分
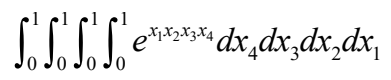
%构造被积函数,x为长为4的列向量或者矩阵(行数为4)。x的每一列表示4维空间中的一个点 f = @(x) exp(prod(x)); n = 10000; X = rand(4,n); % 随机生成n个4维单位超立方体内的点 I = sum(f(x))/n % 用基本的蒙特卡洛法估计积分值 I =1.069245225746442
例2:用蒙特卡洛法计算积分
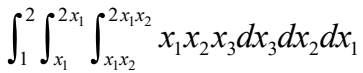
f = @(x) prod(x);n = 100000;% 随机均匀积分区域的点 x1 = unifrnd(1,2,1,n);x2 = unifrnd(1,4,1,n); x3 = unifrnd(1,16,1,n); ind = (x2>=x1)&(x2<=2*x1)&(x3<=2*x1.*x2)&(x3>=x1.*x2); % 积分区间 X = [x1;x2;x3]; I = (4-1)*(16-1)*sum(f(X(:,ind)))/n I = 1.791951576008592e+02
4.3.计算N重积分(等序列分布)
在区间[a,b]中的一个(确定性)点列x1,x2,... ,若对所有的有界黎曼(Riemann)可积函数f(x),均有
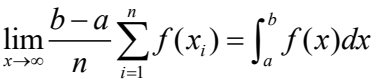
则称该点列在[a,b]中是等分布的。令(ξ)表示ξ的小数部分,即(ξ)=ξ一[ξ],这里[ξ]表示不超过ξ的最大整数。
定理6.1 若θ为一个无理数 ,则数列为xn= (nθ), n =1,2 ,... ,在[0,1]中是等分布的。
对于一般的区间[a,b],可以令un=xn (b-a)+a来得到[a,b]中等分布的点列。对于s重积分,一般是挑选s 个对有理数线性对立的无理数,来得到包含积分区域D的超长方体内的均匀分布的点列。[uai, ubi ],…得到用等分布序列蒙特卡洛法计算的积分的近似值:
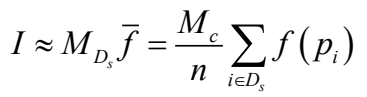
例3:用等序列蒙特卡洛法计算例1的积分
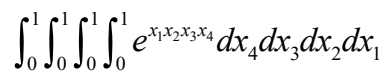
f = @(x) exp(prod(x)); n = 10000; % 选取对有理数独立的无理数sqrt(2),sqrt(3),sqrt(6)/3,sqrt(10)来分成等分布序列 x = bsxfun(@times, repmat(1:n,4,1),[sqrt(2);sqrt(3);sqrt(6)/3;sqrt(10)]); x = mod(x,1);%对1取余运算,即得小数部分 I = sum(f(x))/n % I = 1.069297245824625
例4:用等序列蒙特卡罗法计算积分

包含积分区域的超长方体:
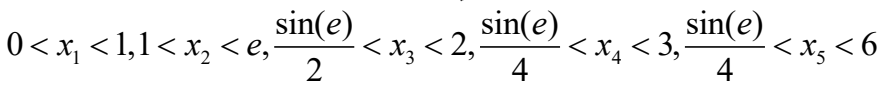
选取对有理数独立的无理数

来生成等分布序列,matlab程序为:
f = @(x) sin(x(1,:).*exp(x(2,:).*sqrt(x(3,:))))+x(4,:).*x(5,:); n = 10000000; x = bsxfun(@times,repmat(1:n.5,1),[sqrt(2);sqrt(3);sqrt(6)/3;sqrt(10);sqrt(19)]); x = mod(x,1); % 一下变换,使得区间(0,1)上的等分布序列变到各层积分区间上去 BminusA = diff([0.5 sin(exp(1))/2 sin(exp(1))/4]) x(2:end,:) = bsxfun(@times,x(2:end,:),BminusA);
相关文章:

MATLAB的编程与应用,匿名函数、嵌套函数、蒙特卡洛法的掌握与使用
目录 1.匿名函数 1.1.匿名函数的定义与分类 1.2.匿名函数在积分和优化中应用 2.嵌套函数 2.1.嵌套函数的定义与分类 2.2.嵌套函数彼此调用关系 2.3.嵌套函数在积分和微分中应用 3.微分和积分 4.蒙特卡洛法 4.1.圆周率的模拟 4.2.计算N重积分(均匀分布&am…...
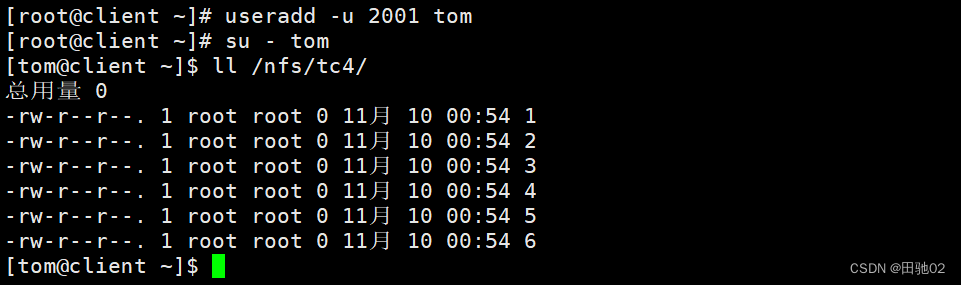
NFS服务器的搭建
架设一台NFS服务器,并按照以下要求配置 准备阶段:准备两台虚拟机,一台作为服务端,一台作为客户端 服务端(Server):192.168.75.139 客户端(Client):192.168.75.160 两…...

安卓Frida 常用脚本
打印调用堆栈, hook 某个方法,想看下调用堆栈,代码如下: function showStacks() {Java.perform(function () {send(Java.use("android.util.Log").getStackTraceString(Java.use("java.lang.Exception").$new()));});} 二,需要hook okhttp3 HttpUrl …...
机器学习数据预处理——Word2Vec的使用
引言: Word2Vec 是一种强大的词向量表示方法,通常通过训练神经网络来学习词汇中的词语嵌入。它可以捕捉词语之间的语义关系,对于许多自然语言处理任务,包括情感分析,都表现出色。 代码: 重点代码&#…...
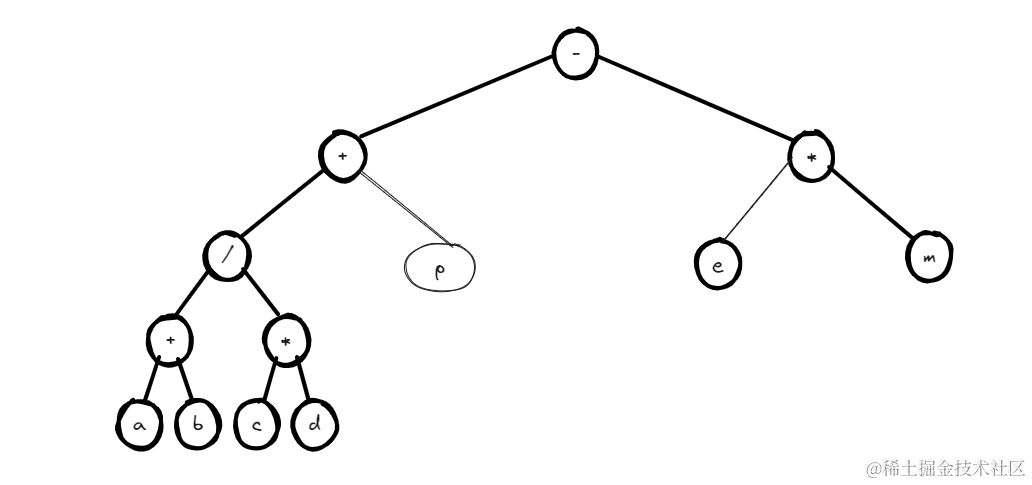
面试算法常考题之-------逆波兰式合集
逆波兰式背景介绍 逆波兰式是一种特殊的数学表达式表示法,它的诞生背景可以追溯到20世纪30年代。当时,波兰数学家Jan Wjtowicz和Wacław Sierpiński提出了一种新的数学表达式表示法,这种表示法将运算符放在操作数之后,而不是传统…...

独热编码和Word2Vec的区别
独热编码和Word2Vec都是自然语言处理中将词向量化的方式,但它们之间并没有直接的关系或依赖性。它们可以被视为在处理词向量时的两种不同方法或策略。 独热编码是一种简单直观的方法,每个词被表示为一个长向量,其中只有一个元素是1࿰…...

RestTemplate.postForEntity 方法进行 HTTP POST 请求
RestTemplate 是 Spring Framework 提供的一个用于处理 HTTP 请求的客户端工具。其中,postForEntity 是 RestTemplate 提供的用于发送 HTTP POST 请求并返回 ResponseEntity 对象的方法。 public <T> ResponseEntity<T> postForEntity(String url, Obj…...

盘点双11!阿里妈妈助这些品牌短视频赢增长!
刚刚!一年一度的双11落下帷幕,很多新变化值得回味。 尽管天气在变凉,但市场出现了逐渐回暖的迹象。在此背景下,大量商家特别关心如何在双11打一场漂亮的胜仗。 卖方如何行动,关键在于买方的变化。在阿里妈妈发布的《…...
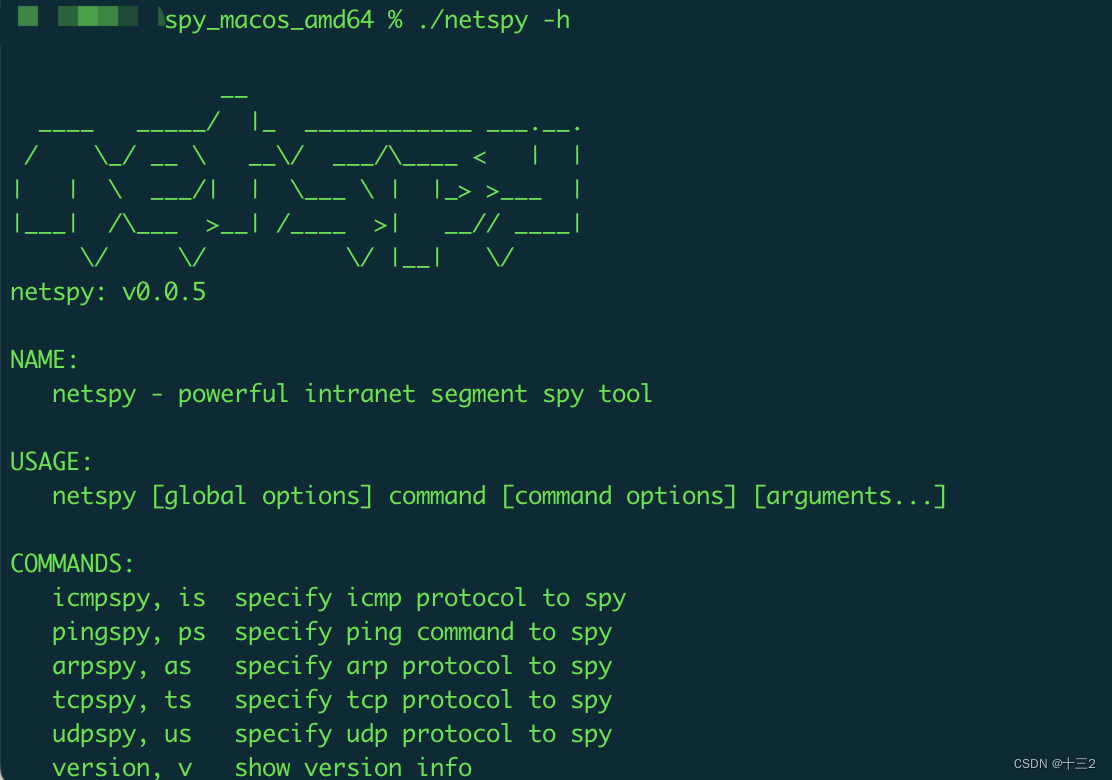
内网可达网段探测netspy- Mac环境
netspy是一款快速探测内网可达网段工具 当我们进入内网后想要扩大战果,那我们可能首先想知道当前主机能通哪些内网段。 netspy正是一款应用而生的小工具,体积较小,速度极快,支持跨平台,支持多种协议探测,…...

Liunx命令汇总
一.用户相关命令 1.1账号管理 创建用户: useradd (选项) 用户名用户口令: passwd (选项) 用户名修改用户: usermod 选项 用户名删除用户: userdel (选项) 用…...
自动控制原理--面试问答题
以下文中的,例如 s_1 为 s下角标1。面试加油! 控制系统的三要素:稳准快。稳,系统最后不能震荡、发散,一定要收敛于某一个值;快,能够迅速达到系统的预设值;准,最后稳态值…...

Word2Vec的缺点
Word2Vec虽然非常强大,但也有一些明显的缺点: 无法处理多义词:Word2Vec会为每个单词分配一个唯一的词向量,这意味着它不能处理具有多种含义的单词。例如,“苹果”可以指一种水果,也可以指一个公司ÿ…...

vue如何解决跨域?原理?
Vue.js本身并不直接解决跨域问题,而是依赖于浏览器的同源策略。但是,Vue提供了一些方法来帮助我们解决跨域问题。 原理: 浏览器的同源策略规定,不同源(协议、域名、端口)之间的网络请求受到限制ÿ…...
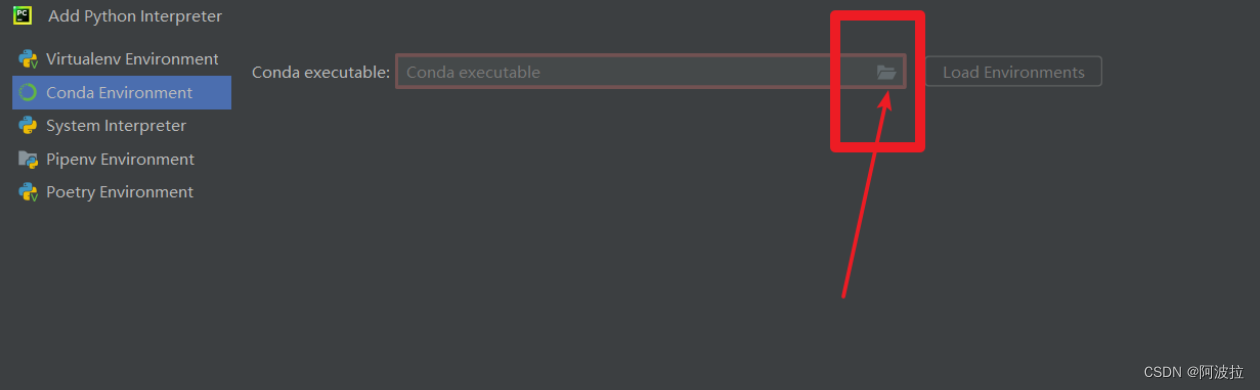
Conda executable is not found 三种问题解决
如果在PyCharm中配置Python解释器时显示“conda executable is not found”错误消息,这意味着PyCharm无法找到您的Conda可执行文件。您可以按照以下步骤解决此问题: 1.方法一 确认Conda已正确安装。请确保您已经正确安装了Anaconda或Minicondaÿ…...
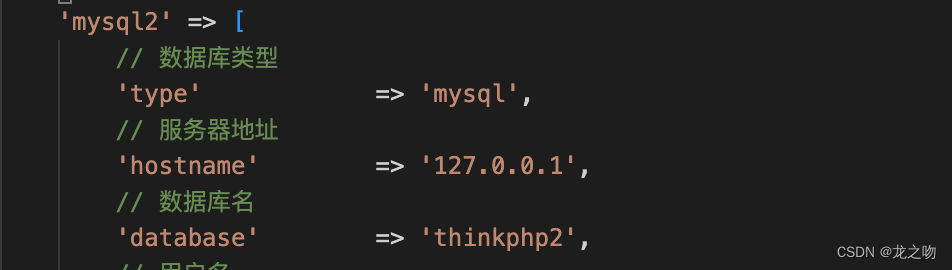
Thinkphp8 - 连接多个数据库
// 数据库连接配置信息connections > [mysql > [// 数据库类型type > mysql,// 服务器地址hostname > 127.0.0.1,// 数据库名database > thinkphp,// 用户名username > env(DB_USER, root),// 密码password >…...
Linux如何修改主机名(hostname)(亲测可用)
文章目录 背景Linux如何修改主机名(hostname)方法方法1. 使用 hostnamectl 命令示例 2. 编辑 /etc/hostname 文件注意事项 背景 我创建虚拟机的时候没设置主机名,现在显示localhost,有点尴尬😅: 需要重新设…...
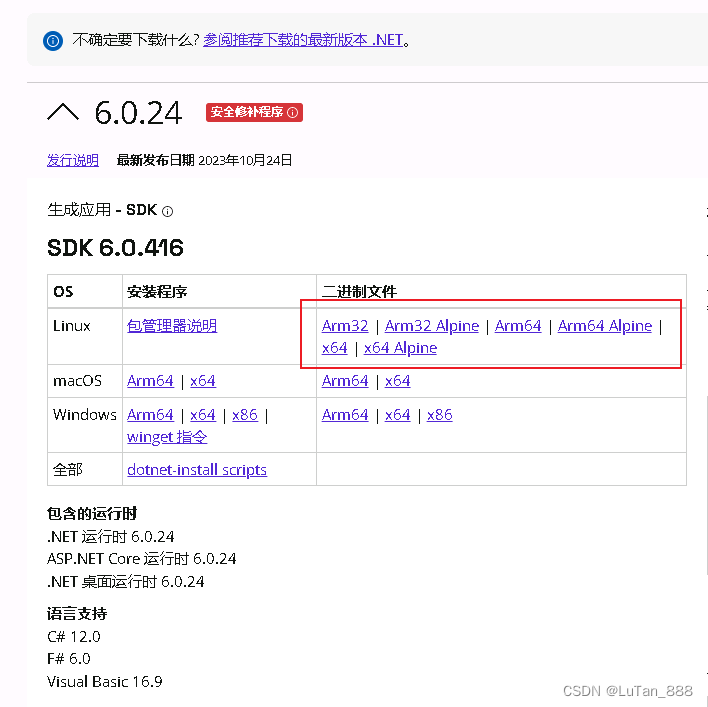
银河麒麟等 Linux系统 安装 .net 3.1,net 6及更高版本的方法
确定 系统的版本。华为鲲鹏处理器是 Arm64位的。 于是到windows 官网下载对应版本 .net sdk 下载地址 https://dotnet.microsoft.com/zh-cn/download/dotnet 2.下载完成后,再linux 服务器 上进入到文件所在目录,建议全英文路径。 然后依次输入以下命令 …...

Unity 使用INI文件存储数据或配置参数预设
法1:调用外部Capi库 具体使用: public class Ini{//读取INI文件需要调用C的APP[System.Runtime.InteropServices.DllImport("kernel32")]private static extern long WritePrivateProfileString(string section, string key, string val, st…...
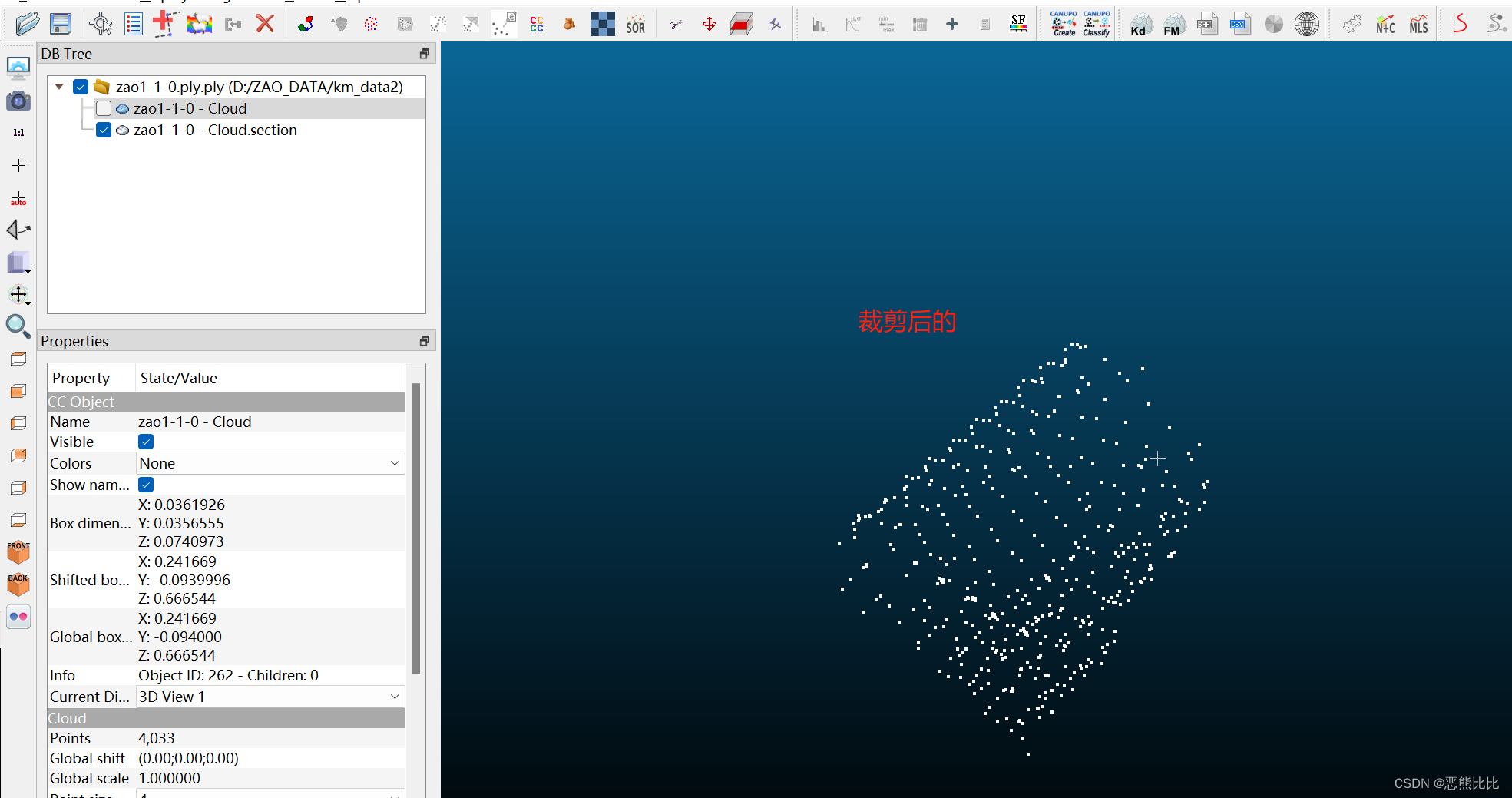
clouldcompare工具使用
文章目录 1.界面1.1 布局1.3 视觉显示方向1.4 放大镜1.5 建立旋转中心2.快速入门2.1 剪裁2.2 多点云拼接 1.界面 1.1 布局 参考:https://blog.csdn.net/lovely_yoshino/article/details/129595201 1.3 视觉显示方向 1.4 放大镜 1.5 建立旋转中心 2.快速入门 2.1 …...
在vue3中使用Element-plus的图标
首先安装Element-Plus-icon # 选择一个你喜欢的包管理器# NPM $ npm install element-plus/icons-vue # Yarn $ yarn add element-plus/icons-vue # pnpm $ pnpm install element-plus/icons-vue 如何使用 Element-Plus-icon官方文档链接Icon 图标 | Element Plus (element-…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...

虚幻基础:角色旋转
能帮到你的话,就给个赞吧 😘 文章目录 移动组件使用控制器所需旋转:组件 使用 控制器旋转将旋转朝向运动:组件 使用 移动方向旋转 控制器旋转和移动旋转 缺点移动旋转:必须移动才能旋转,不移动不旋转控制器…...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...

python读取SQLite表个并生成pdf文件
代码用于创建含50列的SQLite数据库并插入500行随机浮点数据,随后读取数据,通过ReportLab生成横向PDF表格,包含格式化(两位小数)及表头、网格线等美观样式。 # 导入所需库 import sqlite3 # 用于操作…...

MCP和Function Calling
MCP MCP(Model Context Protocol,模型上下文协议) ,2024年11月底,由 Anthropic 推出的一种开放标准,旨在统一大模型与外部数据源和工具之间的通信协议。MCP 的主要目的在于解决当前 AI 模型因数据孤岛限制而…...
