面试算法常考题之-------逆波兰式合集
逆波兰式背景介绍
逆波兰式是一种特殊的数学表达式表示法,它的诞生背景可以追溯到20世纪30年代。当时,波兰数学家Jan Wójtowicz和Wacław Sierpiński提出了一种新的数学表达式表示法,这种表示法将运算符放在操作数之后,而不是传统的数学表达式中的运算符放在操作数之前的表示法。 这种新的表示法被称为逆波兰式,因为它与传统的波兰式数学表达式相反。传统的波兰式数学表达式是一种将运算符放在操作数之前的表示法,例如(2+3)*4。而逆波兰式则是将运算符放在操作数之后,例如2 3 + 4 *。
逆波兰式的出现主要是为了解决传统的数学表达式中的一些问题,例如括号匹配问题。在传统的数学表达式中,括号的嵌套顺序非常重要,如果括号的嵌套顺序不正确,就会导致计算结果错误。而逆波兰式则避免了括号的嵌套问题,因为它不需要使用括号来表示运算顺序。 逆波兰式的出现对计算机科学产生了重要的影响,它被广泛应用于计算机程序设计中,特别是在函数式编程和函数式编译器中。逆波兰式也被用于一些高级编程语言中,例如Lisp和Scheme。
前缀式、后缀式、中缀式的概念
二叉树表达
一个表达式可以使用一棵二叉树来进行一个存储表达,而对应的前、中、后序遍历的结果对应的就是前缀式、中缀式、后缀式。
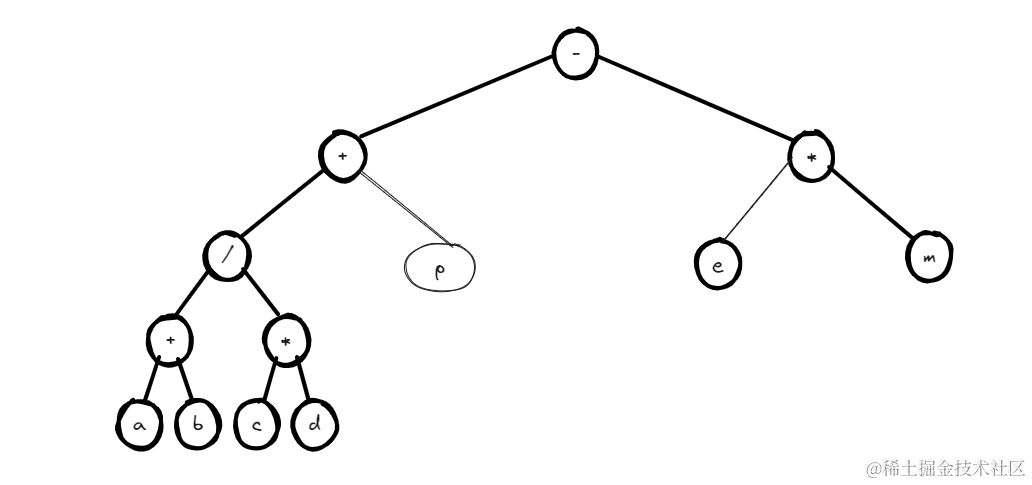
例如表达式**((a+b)/(cd)+p)-(cm)**
对应二叉树:
中缀式
中缀式就是我们人能够认识的表达式格式,如((a+b)/(cd)+p)-(cm),而对应的就是该二叉树的中序遍历得到的结果
前缀式
前缀式就是将该二叉树进行前序遍历得到的结果:-+/+abcdpem
后缀式
后缀式就是将该二叉树进行后序遍历得到的结果:ab+cd*/p+em*-
总结
从前中后序的结构其实不难得出一个很明显的结论:
前缀式往往会将运算符号放在前面,数字放在后面,而后缀式往往是将数字放在前面,运算符号放在后面。
波兰式常见面试算法题:
1.根据前缀式、后缀式求出表达式结果:
后缀式求值(leetcode地址:https://leetcode.cn/problems/8Zf90G/ )
题目简单描述:
根据[ 逆波兰表示法]求该后缀表达式的计算结果。有效的算符包括 `+`、`-`、`*`、`/` 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。说明:整数除法只保留整数部分。给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。示例 1:输入: tokens = ["2","1","+","3","*"]
输出: 9
解释: 该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
其实这个题型是特别简单的,大概思路就是直接遍历tokens,遇见数字就将其放入栈中,遇见运算符将数字取出两个进行运算再将结果放入栈中…即便没遇见过也是很容易想出来的
Go代码展示:
func evalRPN(tokens []string) int {stack := []int{}for _, token := range tokens {val, err := strconv.Atoi(token)if err == nil {stack = append(stack, val)} else {num1, num2 := stack[len(stack)-2], stack[len(stack)-1]stack = stack[:len(stack)-2]switch token {case "+":stack = append(stack, num1+num2)case "-":stack = append(stack, num1-num2)case "*":stack = append(stack, num1*num2)default:stack = append(stack, num1/num2)}}}return stack[0]
}前缀式求值与其原理相同,建议自己可以尝试一下,不过leetcode没有类似题目
中缀式转前缀式、中缀式转后缀式
这种题型其实也挺常考的,之前面试字节一面就出了一个中缀式转后缀式的算法题。。
这类题就没这么容易了,因为有括号的原因,所以其实需要考虑的情况是比较多的。不过基本原理依旧是使用栈~
此题我依旧只解析中缀转后缀的例子,因为中缀转前缀原理依旧一致。
例如该中缀式((a+b)/(cd)+p)-(cm)
其基本原理依旧是遍历一遍中缀式,对’(‘、’)'、‘运算符’、'数字’都会有不同的处理方式
case 1’数字’:直接将其放入结果数组
case 2 ‘(’: 放入栈中
case 3 ‘)’:将其与对应左括号之间的符号出栈放入结果数组
case 4 ‘运算符’:若在栈底, 在括号底, 或者操作符优先级比栈顶的高, 则操作符入栈;否则出栈
举个例子:((a+b)/(cd)+p)-(cm) ---->ab+cd*/p+cm*-
'(' --> stack=['('] res=[]
'(' --> stack['(' , '('] res=[]
'a' --> stack['(' , '('] res=['a']
'+' --> stack['(' , '(' , '+'] res=['a']
'b' --> stack['(' , '(' , '+'] res=['a','b']
')' --> stack['('] res=['a','b','+']
'/' --> stack['(','/'] res=['a','b','+']
'(' --> stack['(','/','('] res=['a','b','+']
'c' --> stack['(','/','('] res=['a','b','+' , 'c']
'*' --> stack['(','/','(' , '*'] res=['a','b','+' , 'c']
'd' --> stack['(','/','(' , '*'] res=['a','b','+' , 'c' , 'd']
')' --> stack['(','/'] res=['a','b','+' , 'c' , 'd','*']
'+' --> stack['(','+'] res=['a','b','+' , 'c' , 'd','*','/']
'p' --> stack['(','+'] res=['a','b','+' , 'c' , 'd','*','/','p']
')' --> stack[] res=['a','b','+' , 'c' , 'd','*','/','p','+']
'-' --> stack['-'] res=['a','b','+' , 'c' , 'd','*','/','p','+']
'(' --> stack['-','('] res=['a','b','+' , 'c' , 'd','*','/','p','+']
'c' --> stack['-','('] res=['a','b','+' , 'c' , 'd','*','/','p','+','c']'*' --> stack['-','(','*'] res=['a','b','+' , 'c' , 'd','*','/','p','+','c']'m' --> stack['-','(','*'] res=['a','b','+' , 'c' , 'd','*','/','p','+','c',''m']')' --> stack[] res=['a','b','+' , 'c' , 'd','*','/','p','+','c',''m','*','-']
每一步按照上述原理进行,就很容易理解如何将中缀式转为后缀式了。而转前缀式同理,感兴趣的小伙伴可以自行去推导一下步骤~
相关文章:

面试算法常考题之-------逆波兰式合集
逆波兰式背景介绍 逆波兰式是一种特殊的数学表达式表示法,它的诞生背景可以追溯到20世纪30年代。当时,波兰数学家Jan Wjtowicz和Wacław Sierpiński提出了一种新的数学表达式表示法,这种表示法将运算符放在操作数之后,而不是传统…...

独热编码和Word2Vec的区别
独热编码和Word2Vec都是自然语言处理中将词向量化的方式,但它们之间并没有直接的关系或依赖性。它们可以被视为在处理词向量时的两种不同方法或策略。 独热编码是一种简单直观的方法,每个词被表示为一个长向量,其中只有一个元素是1࿰…...

RestTemplate.postForEntity 方法进行 HTTP POST 请求
RestTemplate 是 Spring Framework 提供的一个用于处理 HTTP 请求的客户端工具。其中,postForEntity 是 RestTemplate 提供的用于发送 HTTP POST 请求并返回 ResponseEntity 对象的方法。 public <T> ResponseEntity<T> postForEntity(String url, Obj…...

盘点双11!阿里妈妈助这些品牌短视频赢增长!
刚刚!一年一度的双11落下帷幕,很多新变化值得回味。 尽管天气在变凉,但市场出现了逐渐回暖的迹象。在此背景下,大量商家特别关心如何在双11打一场漂亮的胜仗。 卖方如何行动,关键在于买方的变化。在阿里妈妈发布的《…...
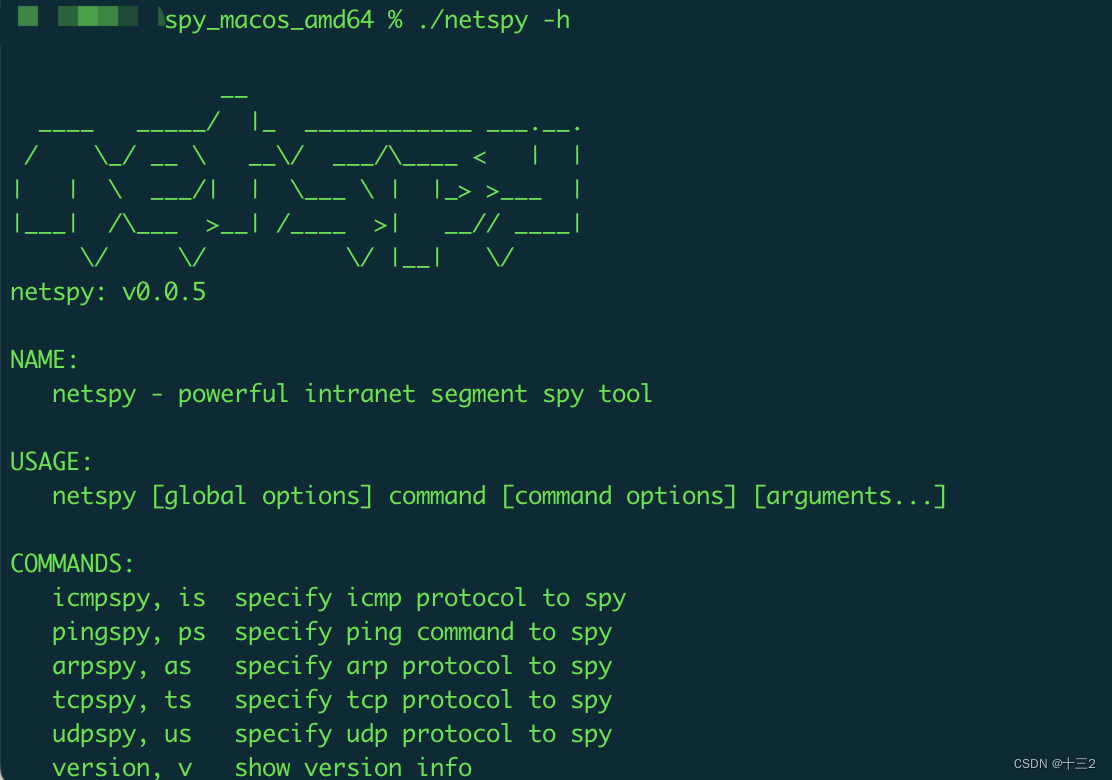
内网可达网段探测netspy- Mac环境
netspy是一款快速探测内网可达网段工具 当我们进入内网后想要扩大战果,那我们可能首先想知道当前主机能通哪些内网段。 netspy正是一款应用而生的小工具,体积较小,速度极快,支持跨平台,支持多种协议探测,…...

Liunx命令汇总
一.用户相关命令 1.1账号管理 创建用户: useradd (选项) 用户名用户口令: passwd (选项) 用户名修改用户: usermod 选项 用户名删除用户: userdel (选项) 用…...
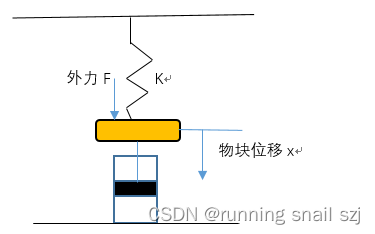
自动控制原理--面试问答题
以下文中的,例如 s_1 为 s下角标1。面试加油! 控制系统的三要素:稳准快。稳,系统最后不能震荡、发散,一定要收敛于某一个值;快,能够迅速达到系统的预设值;准,最后稳态值…...

Word2Vec的缺点
Word2Vec虽然非常强大,但也有一些明显的缺点: 无法处理多义词:Word2Vec会为每个单词分配一个唯一的词向量,这意味着它不能处理具有多种含义的单词。例如,“苹果”可以指一种水果,也可以指一个公司ÿ…...

vue如何解决跨域?原理?
Vue.js本身并不直接解决跨域问题,而是依赖于浏览器的同源策略。但是,Vue提供了一些方法来帮助我们解决跨域问题。 原理: 浏览器的同源策略规定,不同源(协议、域名、端口)之间的网络请求受到限制ÿ…...
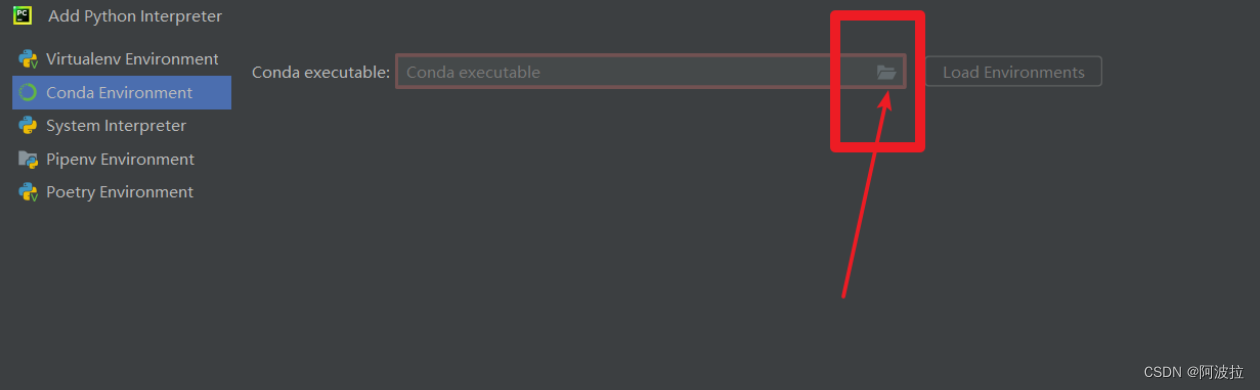
Conda executable is not found 三种问题解决
如果在PyCharm中配置Python解释器时显示“conda executable is not found”错误消息,这意味着PyCharm无法找到您的Conda可执行文件。您可以按照以下步骤解决此问题: 1.方法一 确认Conda已正确安装。请确保您已经正确安装了Anaconda或Minicondaÿ…...
Thinkphp8 - 连接多个数据库
// 数据库连接配置信息connections > [mysql > [// 数据库类型type > mysql,// 服务器地址hostname > 127.0.0.1,// 数据库名database > thinkphp,// 用户名username > env(DB_USER, root),// 密码password >…...
Linux如何修改主机名(hostname)(亲测可用)
文章目录 背景Linux如何修改主机名(hostname)方法方法1. 使用 hostnamectl 命令示例 2. 编辑 /etc/hostname 文件注意事项 背景 我创建虚拟机的时候没设置主机名,现在显示localhost,有点尴尬😅: 需要重新设…...
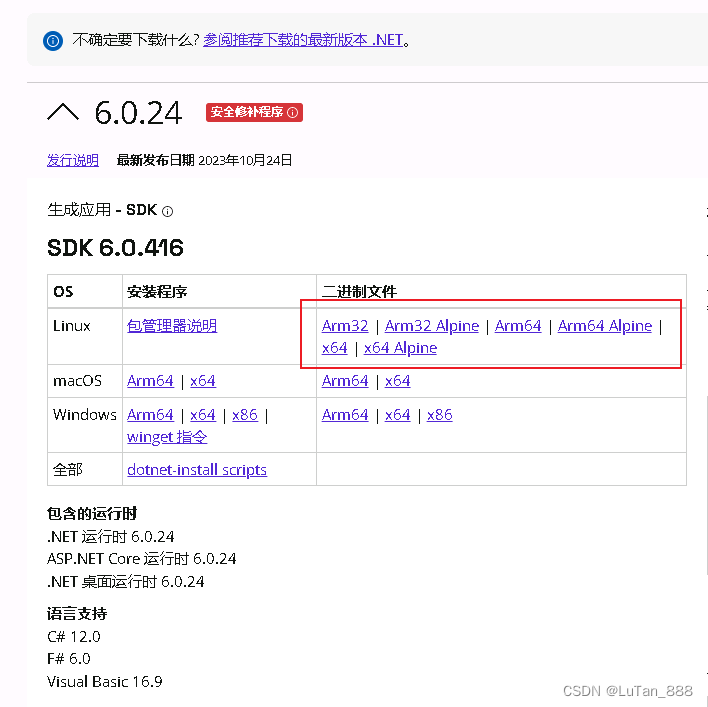
银河麒麟等 Linux系统 安装 .net 3.1,net 6及更高版本的方法
确定 系统的版本。华为鲲鹏处理器是 Arm64位的。 于是到windows 官网下载对应版本 .net sdk 下载地址 https://dotnet.microsoft.com/zh-cn/download/dotnet 2.下载完成后,再linux 服务器 上进入到文件所在目录,建议全英文路径。 然后依次输入以下命令 …...

Unity 使用INI文件存储数据或配置参数预设
法1:调用外部Capi库 具体使用: public class Ini{//读取INI文件需要调用C的APP[System.Runtime.InteropServices.DllImport("kernel32")]private static extern long WritePrivateProfileString(string section, string key, string val, st…...
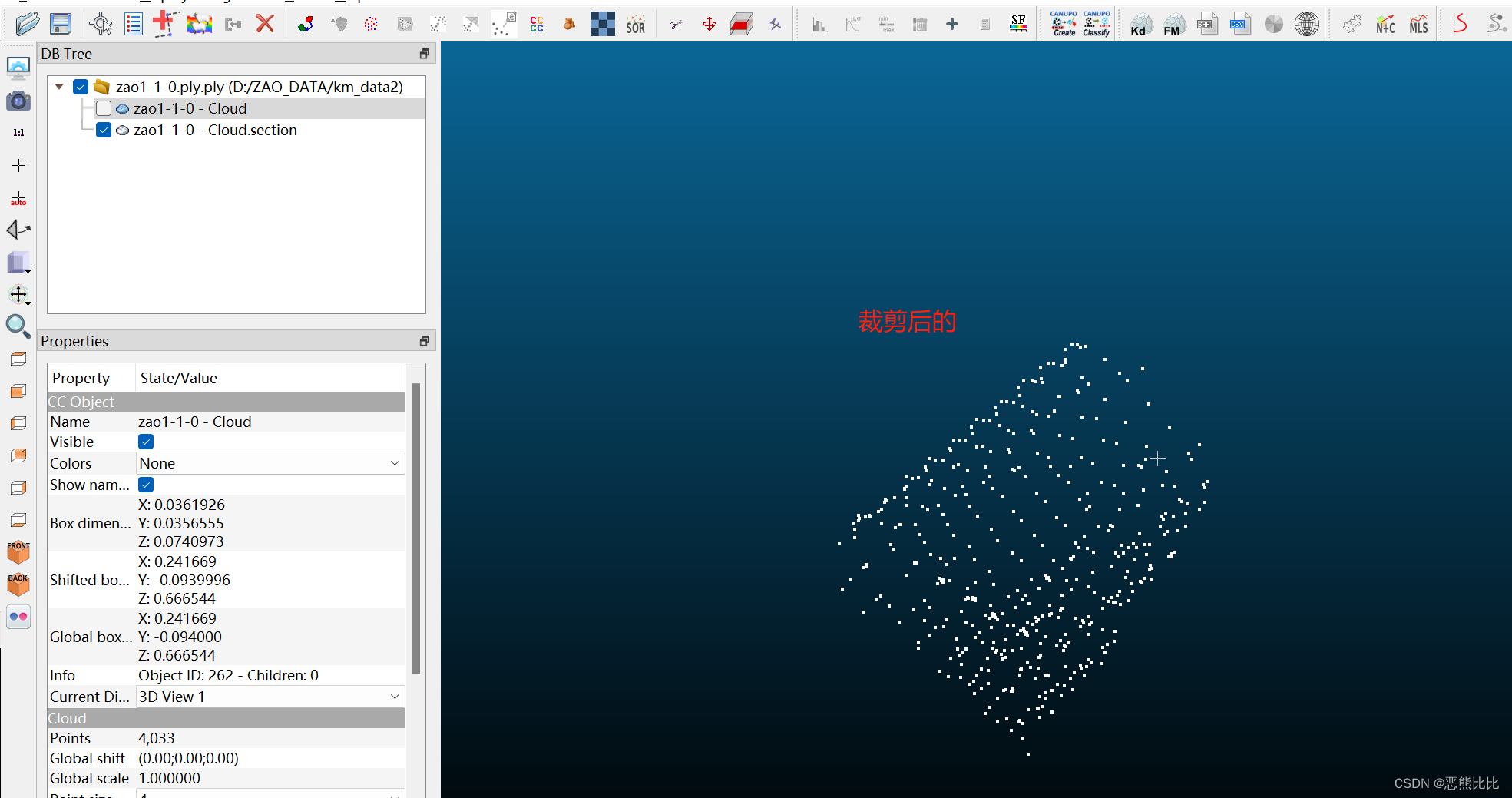
clouldcompare工具使用
文章目录 1.界面1.1 布局1.3 视觉显示方向1.4 放大镜1.5 建立旋转中心2.快速入门2.1 剪裁2.2 多点云拼接 1.界面 1.1 布局 参考:https://blog.csdn.net/lovely_yoshino/article/details/129595201 1.3 视觉显示方向 1.4 放大镜 1.5 建立旋转中心 2.快速入门 2.1 …...
在vue3中使用Element-plus的图标
首先安装Element-Plus-icon # 选择一个你喜欢的包管理器# NPM $ npm install element-plus/icons-vue # Yarn $ yarn add element-plus/icons-vue # pnpm $ pnpm install element-plus/icons-vue 如何使用 Element-Plus-icon官方文档链接Icon 图标 | Element Plus (element-…...
图扑智慧农业:农林牧数据可视化监控平台
数字农业是一种现代农业方式,它将信息作为农业生产的重要元素,并利用现代信息技术进行农业生产过程的实时可视化、数字化设计和信息化管理。能将信息技术与农业生产的各个环节有机融合,对于改造传统农业和改变农业生产方式具有重要意义。 图…...
)
js 加解密 jsencrypt(非对称加密 rsa)
这是一个非对称加密的库,可以进行 rsa 加解密 使用方法 安装 npm install jsencrypt --save jsencrypt rsa 加解密 let rsaStr "这就是一个RSA加密的测试";let jsencryptObj new jsencrypt();jsencryptObj.getKey(); //这个方法用来生成一个密钥对…...
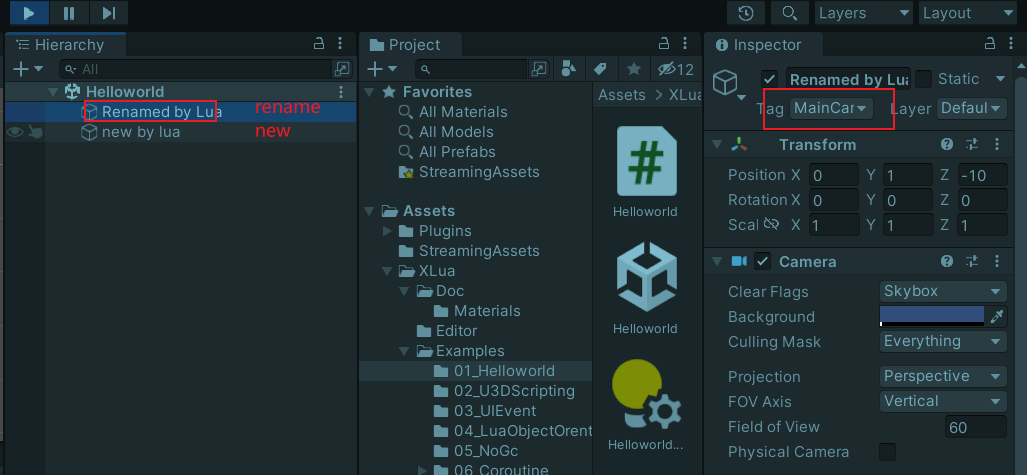
xlua游戏热更新(lua访问C#)
CS.UnityEngine静态方法访问unity虚拟机 创建游戏物体 CS.UnityEngine.GameObject(new by lua);静态属性 CS.UnityEngine.GameObject(new by lua); -- 创建 local camera CS.UnityEngine.GameObject.Find(Main Camera); --查找 camera.name Renamed by Lua;访问组件 loca…...

04-Spring中Bean的作用域
Bean的作用域 scope的属性值 属性值作用singleton默认单例prototype原型每调用一次getBean()方法则获取一个新的Bean对象 , 每次注入的时候都是新对象request一个请求对应一个Bean仅限于在WEB应用中使用 , 需要引入web的框架如SpringMvc(global) session一个会话对应一个Bean…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
