js 加解密 jsencrypt(非对称加密 rsa)
这是一个非对称加密的库,可以进行 rsa 加解密
使用方法
安装
npm install jsencrypt --save
jsencrypt rsa 加解密
let rsaStr = "这就是一个RSA加密的测试";let jsencryptObj = new jsencrypt();jsencryptObj.getKey(); //这个方法用来生成一个密钥对let publicKey = jsencryptObj.getPublicKey(); //得到公钥let privateKey = jsencryptObj.getPrivateKey(); //得到私钥let result1 = jsencryptObj.encrypt(rsaStr); //加密var st = jsencryptObj.decrypt(result1); //解密
上面是最基本的用法, 但是我们通常是 从前端接收到后端的数据,然后再去解密的,这里我们用 php 做后端加密数据,再用js 作前端来解密数据
这里我们首先产生一个公,私钥对
公钥字串
-----BEGIN PRIVATE KEY-----
MIIEvQIBADANBgkqhkiG9w0BAQEFAASCBKcwggSjAgEAAoIBAQDNW0UTqFuKE4rA
NeUkPC5GhB8XcrcepL3jFLhK7YfD/spropSxqCH6PQ+VchIsCAGAtrKVyABjsGbU
yWa5ww90Z0FHo4UR2WnucvAlzmS2ENXSCif7W5Tj3lUddM9ZURwz3lWTA7QZLoIf
4AfR0zPJq0XhYzaAOdNoFm5AoZ27zSD3uBBL4vOXEfwZcOP6fQLrUkwSnKPj08BK
RRmwie3pJ2pU7eBX9NkS9oWU5u74LzJ+u4W6pdYGZo/TjTCyPF44Udkx+Rp9+BUg
Wd23rcVF2VmdWsZsgcIugjH/8z1sYbF0GdGe9CFM2CydxpzE91vqHEm7PaeaBWbe
JxsOdowdAgMBAAECggEAW04waWwav0qvD4UnC7RiUuIdvNw5hTt0XknxIwd3rPJV
aAQSnucFrHCHxEfCwqcQm/0fbC9P1QMyxXuC3CdZcMUUJlkTKnuDeQzLr9OTvcvA
djIj0sPGcIaDS6SLKMhChOFfJQ2pfuTJ4IhIkceZKBqp6GunaN3NHGOUw9HYAw6G
XrRvUXr4KSXwqAF83ufSKzV7jrsVu6Pn/59svwrJdYZp3jZ6eqDn6o5PLbVw55GM
81JsrDbv3gxcAsgbZnx9GlupgrRqto7MEJlF4q5sybCksDHbGWL2i1zRfbrtz93W
u56jEJKCDZq/cjRt19RKf03RaGgLa+Q+hVMEzrYWgQKBgQDyLG9pppRexlB3zp17
dJnesXXdfda9dy183e7bv9XTtrcZkbzLeOlWKVQcXgPozsQSPeoylGnq07ohVIze
Zn5DkRJ5G6A5L4RUUNva8B4IYue62yPG9is+UgENLZe77xh0/vBD8TGACX7FTvcp
qeN4u4aFJXdJu4ZDa7mBHdvIfQKBgQDZFLkqljYC8Lvy0GYgeEgBxOTwN78s1Wkg
38G6oN++glFBX6P0T7TffWv2AGKTNCi6xfVRpnPmKfuUV7qo6ltHp2PjkUhylVQy
9OyW4rA0cDFj/ng6PCa0gzApHOzE1zVgLyXJiEkB0IHZ96+Vk+T2GcT7zMAaqSm2
sgM+QcrEIQKBgHU8+8bK5QMowKXveZ/dp+v+P1A17nKUsonDqzHpIew3hVa0jhB2
/Yc/xL9i6EOZbaRjIvDPlqMfUvl1xCiat7+gCLBmpl9o2Ig1COpp2jA3KXX1RtG4
NOEbs/ScQNuzeUSScuCBcHRKpHuCqfcajsvRBOOKasBgLzSOfyS5vr/FAoGBALSy
vGPHv9P4weqgMLLMjNv0IsIXFWrjhmwX9fI9IaI6Zhrt2tNuWdhDVc/jiCqSm2jF
iaxay1UHE2TrFfSviCYAH3T5pX3D8d+s4xfCQPyVe3eKBlgrY+iU300Jx8kef06+
UE0Oxf7dqole1OjEwC1fTApx6GMI9zEdwvda2schAoGAKlzCLgEK3a/U6Tl/WVmo
at34IXFSK+GRQvuMYube6KYndwnWq5n6eqNN2FbrcDMhK+lsGz2f4BVvftFZeCu1
SHCoHpU9wObmQb64ZYf8BrIOkSCF6qDlQGoLaJhpCtLmzAxgABu4Ou1lC/dW7zcK
vnjq5XBRANexvfDtqU0MM28=
-----END PRIVATE KEY-----
私钥字串
-----BEGIN PUBLIC KEY-----
MIIBIjANBgkqhkiG9w0BAQEFAAOCAQ8AMIIBCgKCAQEAzVtFE6hbihOKwDXlJDwu
RoQfF3K3HqS94xS4Su2Hw/7Ka6KUsagh+j0PlXISLAgBgLaylcgAY7Bm1MlmucMP
dGdBR6OFEdlp7nLwJc5kthDV0gon+1uU495VHXTPWVEcM95VkwO0GS6CH+AH0dMz
yatF4WM2gDnTaBZuQKGdu80g97gQS+LzlxH8GXDj+n0C61JMEpyj49PASkUZsInt
6SdqVO3gV/TZEvaFlObu+C8yfruFuqXWBmaP040wsjxeOFHZMfkaffgVIFndt63F
RdlZnVrGbIHCLoIx//M9bGGxdBnRnvQhTNgsncacxPdb6hxJuz2nmgVm3icbDnaM
HQIDAQAB
-----END PUBLIC KEY-----
在php中利用公钥来加密 (注意一下,公钥字符串的定义,是使用的 长字符定义的方式)
php rsa 加密很简单
$str="这是一个后端加密,前端解密的实验,RSA算法";//这里得到了私钥的密钥$private_key = <<<"eto"
-----BEGIN PRIVATE KEY-----
MIIEvQIBADANBgkqhkiG9w0BAQEFAASCBKcwggSjAgEAAoIBAQDNW0UTqFuKE4rA
NeUkPC5GhB8XcrcepL3jFLhK7YfD/spropSxqCH6PQ+VchIsCAGAtrKVyABjsGbU
yWa5ww90Z0FHo4UR2WnucvAlzmS2ENXSCif7W5Tj3lUddM9ZURwz3lWTA7QZLoIf
4AfR0zPJq0XhYzaAOdNoFm5AoZ27zSD3uBBL4vOXEfwZcOP6fQLrUkwSnKPj08BK
RRmwie3pJ2pU7eBX9NkS9oWU5u74LzJ+u4W6pdYGZo/TjTCyPF44Udkx+Rp9+BUg
Wd23rcVF2VmdWsZsgcIugjH/8z1sYbF0GdGe9CFM2CydxpzE91vqHEm7PaeaBWbe
JxsOdowdAgMBAAECggEAW04waWwav0qvD4UnC7RiUuIdvNw5hTt0XknxIwd3rPJV
aAQSnucFrHCHxEfCwqcQm/0fbC9P1QMyxXuC3CdZcMUUJlkTKnuDeQzLr9OTvcvA
djIj0sPGcIaDS6SLKMhChOFfJQ2pfuTJ4IhIkceZKBqp6GunaN3NHGOUw9HYAw6G
XrRvUXr4KSXwqAF83ufSKzV7jrsVu6Pn/59svwrJdYZp3jZ6eqDn6o5PLbVw55GM
81JsrDbv3gxcAsgbZnx9GlupgrRqto7MEJlF4q5sybCksDHbGWL2i1zRfbrtz93W
u56jEJKCDZq/cjRt19RKf03RaGgLa+Q+hVMEzrYWgQKBgQDyLG9pppRexlB3zp17
dJnesXXdfda9dy183e7bv9XTtrcZkbzLeOlWKVQcXgPozsQSPeoylGnq07ohVIze
Zn5DkRJ5G6A5L4RUUNva8B4IYue62yPG9is+UgENLZe77xh0/vBD8TGACX7FTvcp
qeN4u4aFJXdJu4ZDa7mBHdvIfQKBgQDZFLkqljYC8Lvy0GYgeEgBxOTwN78s1Wkg
38G6oN++glFBX6P0T7TffWv2AGKTNCi6xfVRpnPmKfuUV7qo6ltHp2PjkUhylVQy
9OyW4rA0cDFj/ng6PCa0gzApHOzE1zVgLyXJiEkB0IHZ96+Vk+T2GcT7zMAaqSm2
sgM+QcrEIQKBgHU8+8bK5QMowKXveZ/dp+v+P1A17nKUsonDqzHpIew3hVa0jhB2
/Yc/xL9i6EOZbaRjIvDPlqMfUvl1xCiat7+gCLBmpl9o2Ig1COpp2jA3KXX1RtG4
NOEbs/ScQNuzeUSScuCBcHRKpHuCqfcajsvRBOOKasBgLzSOfyS5vr/FAoGBALSy
vGPHv9P4weqgMLLMjNv0IsIXFWrjhmwX9fI9IaI6Zhrt2tNuWdhDVc/jiCqSm2jF
iaxay1UHE2TrFfSviCYAH3T5pX3D8d+s4xfCQPyVe3eKBlgrY+iU300Jx8kef06+
UE0Oxf7dqole1OjEwC1fTApx6GMI9zEdwvda2schAoGAKlzCLgEK3a/U6Tl/WVmo
at34IXFSK+GRQvuMYube6KYndwnWq5n6eqNN2FbrcDMhK+lsGz2f4BVvftFZeCu1
SHCoHpU9wObmQb64ZYf8BrIOkSCF6qDlQGoLaJhpCtLmzAxgABu4Ou1lC/dW7zcK
vnjq5XBRANexvfDtqU0MM28=
-----END PRIVATE KEY-----
eto;openssl_private_encrypt($str,$result,$private_key);//参数中的 $result 就是 rsa 的加密结果dump($result);//加密结果是一个二进制的数据,所以我们以base64一下传给前端echo base64_encode($result);
//结果 : CcNW2lFUQHYAhz60CHpwPbCXlqpZYQIK0gJZWeE5IPJG9Hw8e3arJ3j9PqsLrDyCRub5pOJQQqrOpMIyOZCP05BUcJRpBi+DR6Z7MrJuqw7B+283mZO/bPllhj6SILz7BD17zodmzw9E+QZG/DdLouOGVKHiirU9STFRgD3DiN93Rj8JzK70gNCnWrEtrCfHA+NdagLCdUEITxf3DL574ZlUXrSIvCj/Rf48/gXWypxG333Pp/IswHtBL6UOuiKGyY//t2aTqCgWRT8qy3nvWAXfH4WgePe+irPYxwOQkXh90oSiRDT2gLhnLV3ZWSSMqaAfCgKNKsCF+uGdONwMiw==
js 进行解密
把php中的结果字符串得到
解密失败, 有太神帮我看一下 问题在哪相关文章:
)
js 加解密 jsencrypt(非对称加密 rsa)
这是一个非对称加密的库,可以进行 rsa 加解密 使用方法 安装 npm install jsencrypt --save jsencrypt rsa 加解密 let rsaStr "这就是一个RSA加密的测试";let jsencryptObj new jsencrypt();jsencryptObj.getKey(); //这个方法用来生成一个密钥对…...
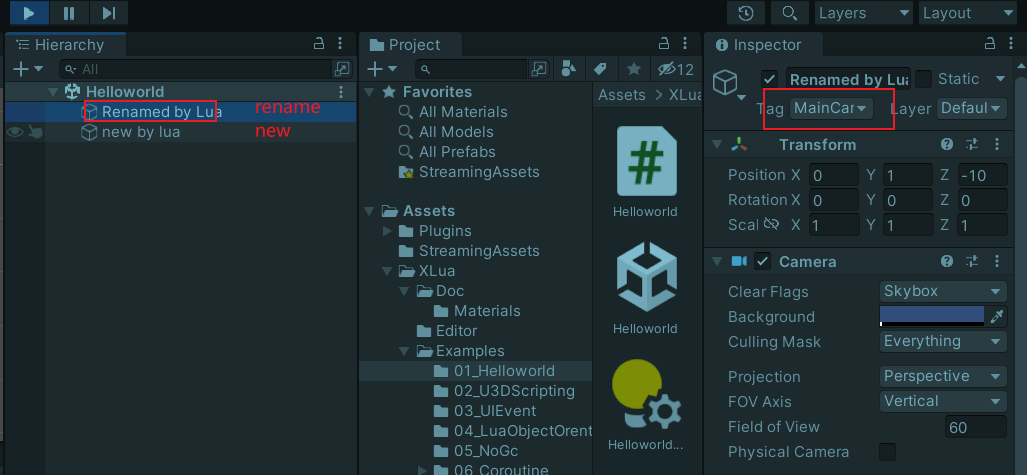
xlua游戏热更新(lua访问C#)
CS.UnityEngine静态方法访问unity虚拟机 创建游戏物体 CS.UnityEngine.GameObject(new by lua);静态属性 CS.UnityEngine.GameObject(new by lua); -- 创建 local camera CS.UnityEngine.GameObject.Find(Main Camera); --查找 camera.name Renamed by Lua;访问组件 loca…...

04-Spring中Bean的作用域
Bean的作用域 scope的属性值 属性值作用singleton默认单例prototype原型每调用一次getBean()方法则获取一个新的Bean对象 , 每次注入的时候都是新对象request一个请求对应一个Bean仅限于在WEB应用中使用 , 需要引入web的框架如SpringMvc(global) session一个会话对应一个Bean…...

xlua游戏热更新(C#访问lua)
xlua作为Unity资源热更新的重要解决方案api,在Tecent重多游戏中被采用,本文通过案例去讲解xlua代码结构层次。 /** Tencent is pleased to support the open source community by making xLua available.* Copyright (C) 2016 THL A29 Limited, a Tence…...
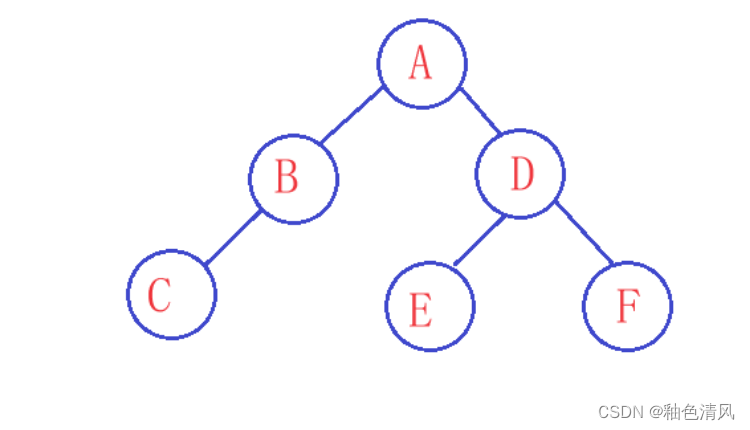
【数据结构】二叉树经典例题---<你真的掌握二叉树了吗?>(第一弹)
一、已知一颗二叉树如下图,试求: (1)该二叉树前序、中序和后序遍历的结果。 (2)该二叉树是否为满二叉树?是否为完全二叉树? (3)将它转换成对应的树或森林。 (4)这颗二叉树的深度为多少? (5)试对该二叉树进行前序线索化。 (6)试对…...
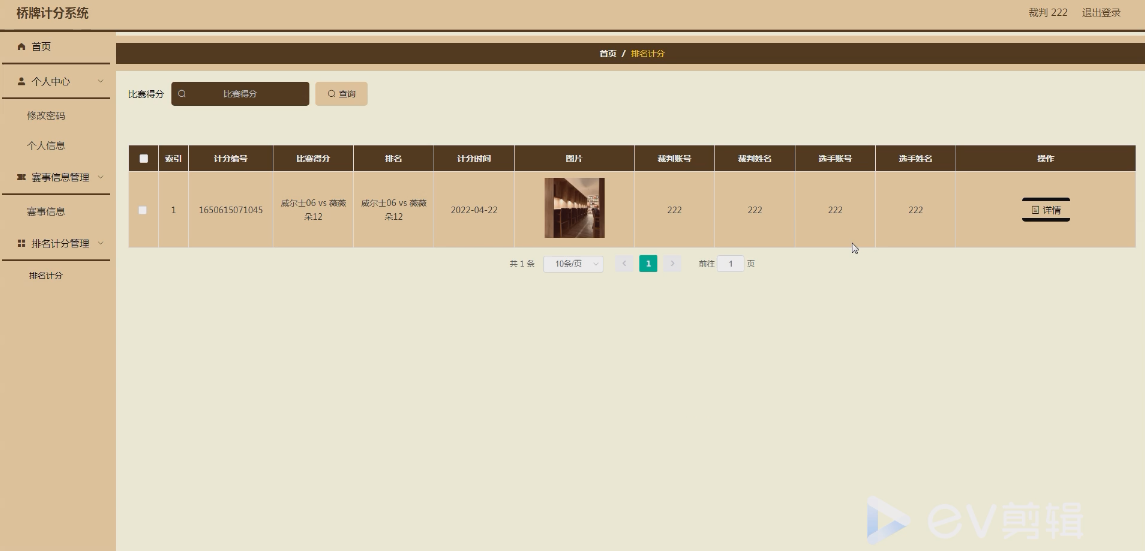
基于springboot实现桥牌计分管理系统项目【项目源码】
基于springboot实现桥牌计分管理系统演示 JAVA简介 JavaScript是一种网络脚本语言,广泛运用于web应用开发,可以用来添加网页的格式动态效果,该语言不用进行预编译就直接运行,可以直接嵌入HTML语言中,写成js语言&#…...
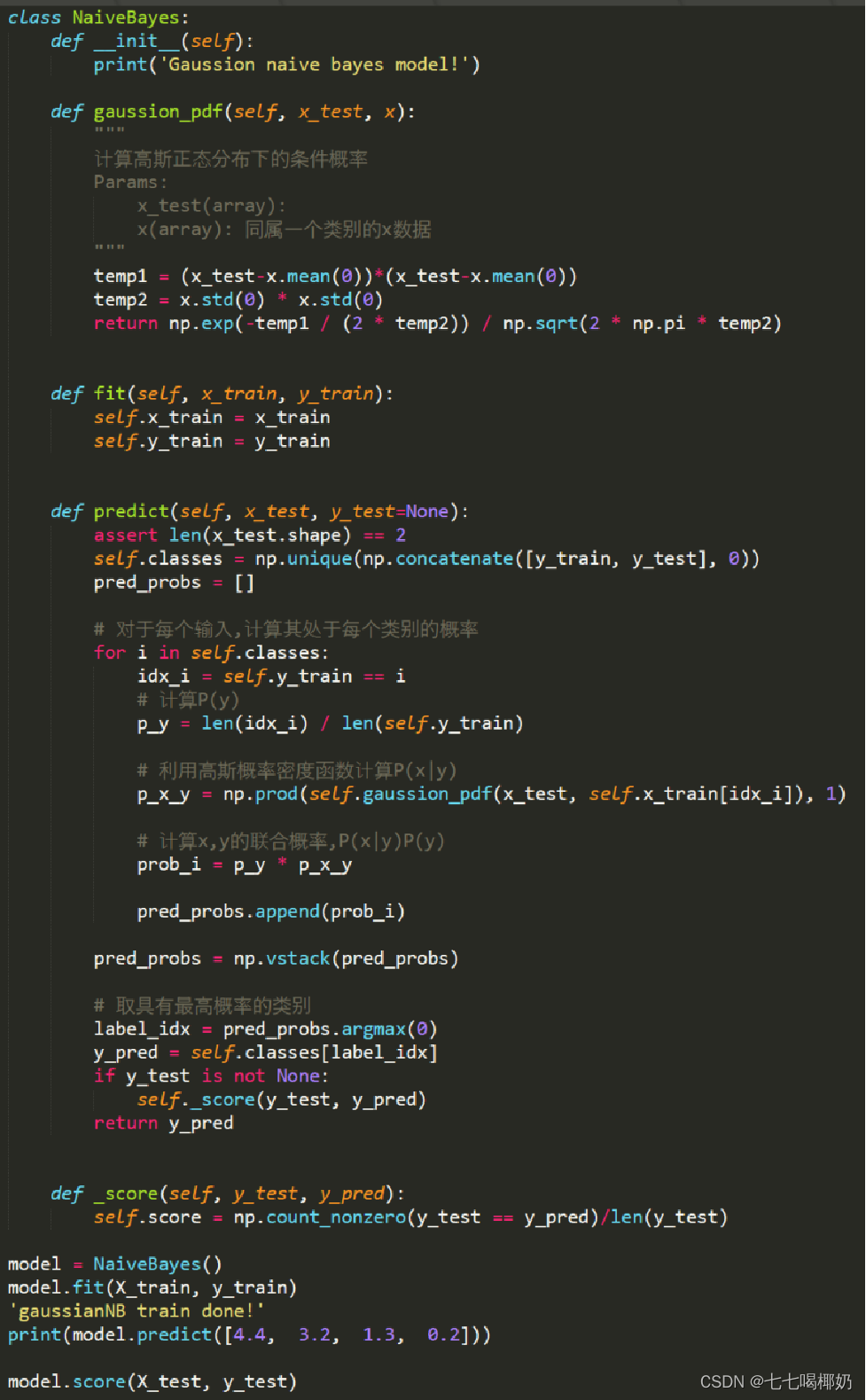
机器学习——朴素贝叶斯
目录 一、贝叶斯方法 背景知识 贝叶斯公式 二、朴素贝叶斯原理 判别模型和生成模型 1.朴素贝叶斯法是典型的生成学习方法 2.朴素贝叶斯法的基本假设是条件独立性 3.朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测 用于文…...

【PTE-day07 文件上传2】
1、常见的绕过方式 (1)畸形后缀名绕过 .php、.pht、.php3、.php4、.php5、.php2、.phtml、.pHp、.html、.Htm......(2)双写过滤字符绕过 (3).htaccess文件绕过 <FilesMatch "jpg"> SetHandler application/x-httpd-php...
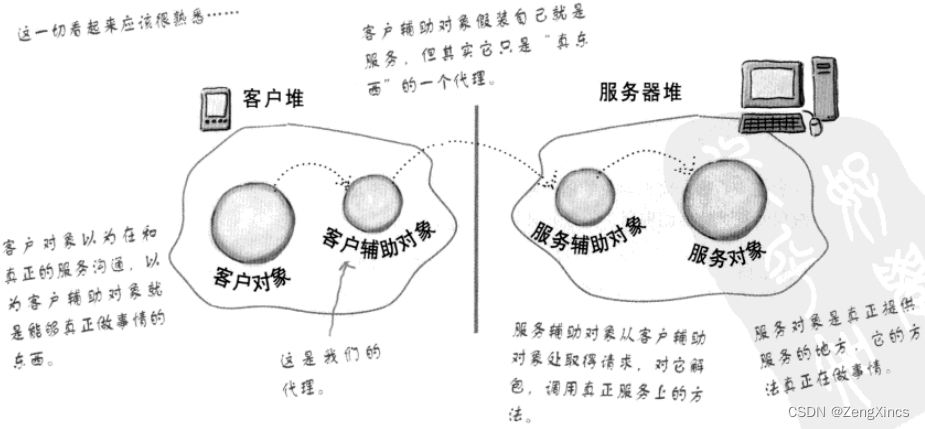
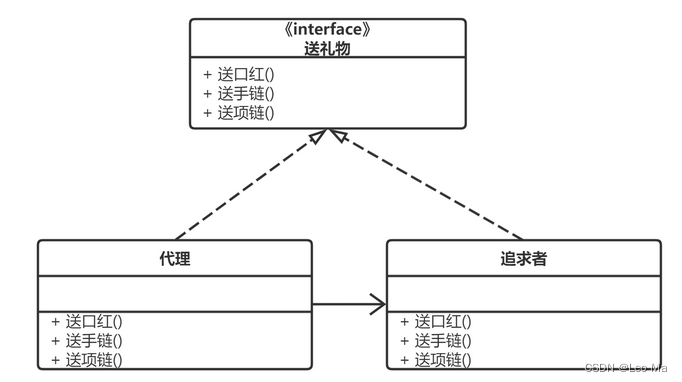
设计模式之十一:代理模式
代理可以控制和管理访问。 RMI提供了客户辅助对象和服务辅助对象,为客户辅助对象创建和服务对象相同的方法。RMI的好处在于你不必亲自写任何网络或I/O代码。客户程序调用远程方法就和运行在客户自己本地JVM对对象进行正常方法调用一样。 步骤一:制作远程…...

在spring boot中调用第三方接口时重试问题
文章目录 前言 spring-retry对第三方接口做重试,和处理操作 一、引入依赖 <!--重试请求的注解依赖--><dependency><groupId>org.springframework.retry</groupId><artifactId>spring-retry</artifactId></dependency>&l…...

记录一次多数据源配置失效的情况
说明:在一些复杂的业务情景,比如我们需要在一个订单审核通过后,在将数据库状态修改的同时,将订单与订单详细这两条数据写入到另一个数据库中。我们就可以通过在配置文件中,配置多数据源,然后通过在Mapper的…...

EasyExcel导出替换列中的变量
基于easyexcel2.0版本 easyexcel官网:https://easyexcel.opensource.alibaba.com/docs/2.x/quickstart/write 测试代码地址:https://gitee.com/wangtianwen1996/cento-practice/blob/master/src/test/java/com/xiaobai/easyexcel/DynamicHeadTest.java …...

机器人规划算法——将多边形障碍物离散到地图像素点上?
问题一:如何判断一个点是否在多边形区域内? 方法1:向量叉乘判别法 设多边形的顶点依次为A1,A2…An,要判断的点为P,那么分别计算向量PA1叉乘向量PA2,向量PA2叉乘向量PA3,…ÿ…...
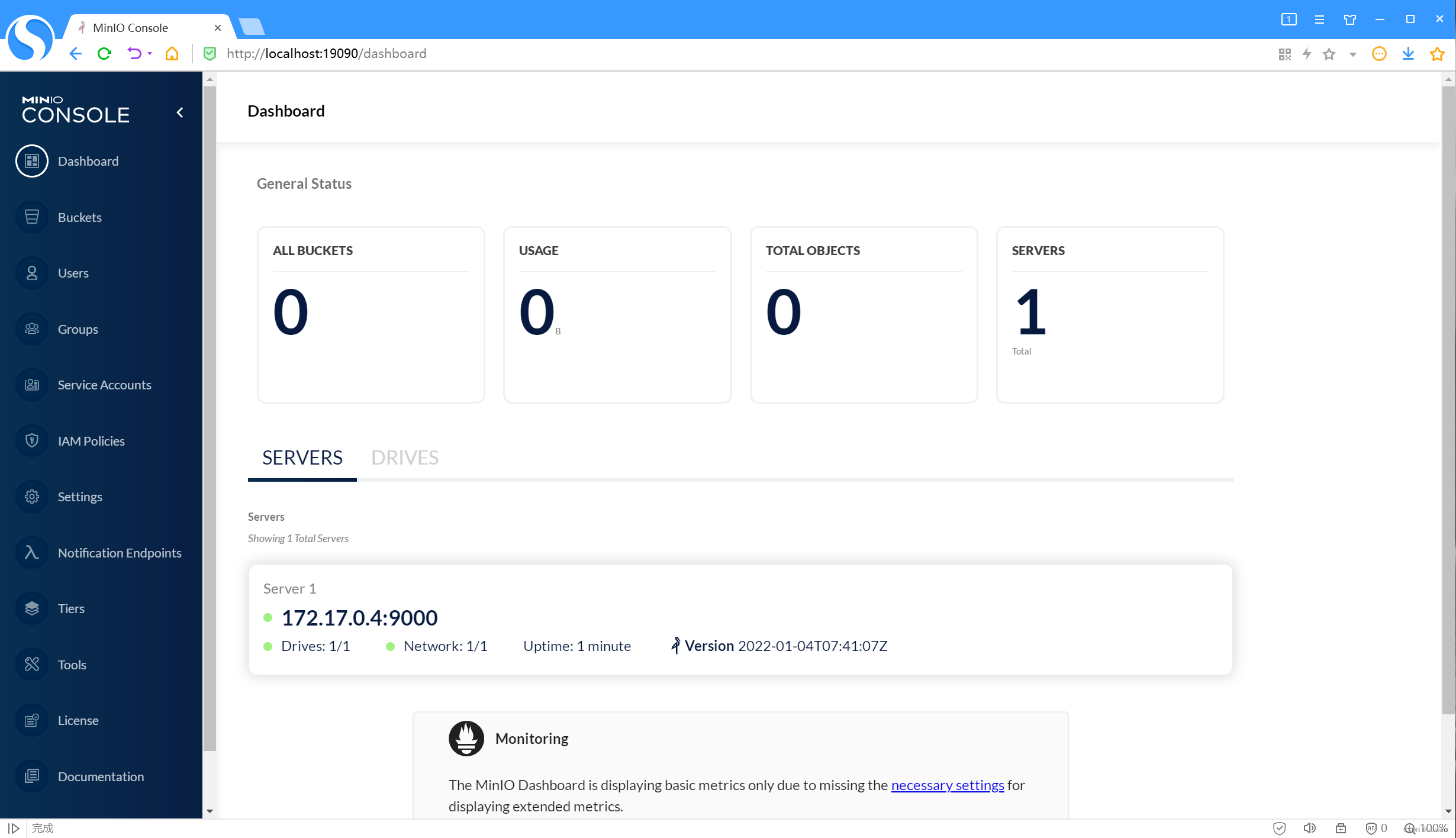
windows11使用docker部署安装minio
时间 2023-11-08 windows11使用docker部署安装minio 目录 1.docker 下载镜像2.docker安装镜像3.访问控制台4.安装问题解决5.使用教程 1.docker 下载镜像 调整镜像源到国内,否则会很慢 docker pull minio/minio2.docker安装镜像 设置用户名和密码时需要注意&…...

【JavaEESpring】Spring Web MVC⼊⻔
Spring Web MVC 1. 什么是 Spring Web MVC1.1 什么是 MVC ?1.2 是什么 Spring MVC? 2. 学习 Spring MVC2.1 建立连接2.2 请求2.3 响应 3. 相关代码链接 1. 什么是 Spring Web MVC 官⽅对于 Spring MVC 的描述是这样的: 1.1 什么是 MVC ? MVC 是 Model View C…...
flutter逆向 ACTF native app
前言 算了一下好长时间没打过CTF了,前两天看到ACTF逆向有道flutter逆向题就过来玩玩啦,花了一个下午做完了.说来也巧,我给DASCTF十月赛出的逆向题其中一道也是flutter,不过那题我难度降的相当之低啦,不知道有多少人做出来了呢~ 还原函数名 flutter逆向的一大难点就是不知道l…...
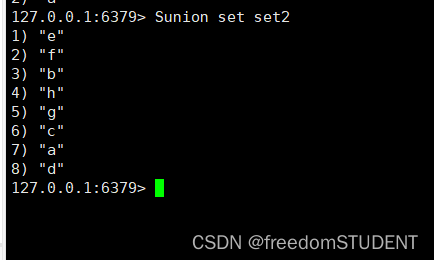
【Redis】set 集合
上一篇:list 列表 https://blog.csdn.net/m0_67930426/article/details/134364315?spm1001.2014.3001.5501 目录 Sadd Smembers Sismember Scard Srem 编辑Srandomember Spop Smove 集合类 Sdiff Sinter Sunion 官网 https://redis.io/commands/?…...
【算法与设计模式】
一、数据结构与算法 1、算法性能评估 时间复杂度、空间复杂度 2、数据结构 数组与列表 队列 堆栈 链表 二叉树 多叉树 递归算法 二、设计模式 1、单例 (1)GIL:线程互斥锁。保证同一时刻只有一个线程在进行。 (2)…...

Javaweb之javascript的小案例的详细解析
1.5.4 案例 1.5.4.1 需求说明 鲁迅说的好,光说不练假把式,光练不说傻把式。所以接下来我们需要通过案例来加强对于上述DOM知识的掌握。需求如下3个: 点亮灯泡 将所有的div标签的标签体内容后面加上:very good 使所有的复选框呈现被选中的…...
Vant 移动端UI 组件自动引入
Vue项目中安装Vant # Vue 3 项目,安装最新版 Vant npm i vant 组件按需引入配置 Vant按需引入- - -安装:unplugin-vue-components 插件 unplugin-vue-components 插件可以在Vue文件中自动引入组件(包括项目自身的组件和各种组件库中的组件&…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
