xlua游戏热更新(lua访问C#)
CS.UnityEngine静态方法访问unity虚拟机
创建游戏物体
CS.UnityEngine.GameObject('new by lua');
静态属性
CS.UnityEngine.GameObject('new by lua'); -- 创建
local camera = CS.UnityEngine.GameObject.Find('Main Camera'); --查找
camera.name = 'Renamed by Lua';
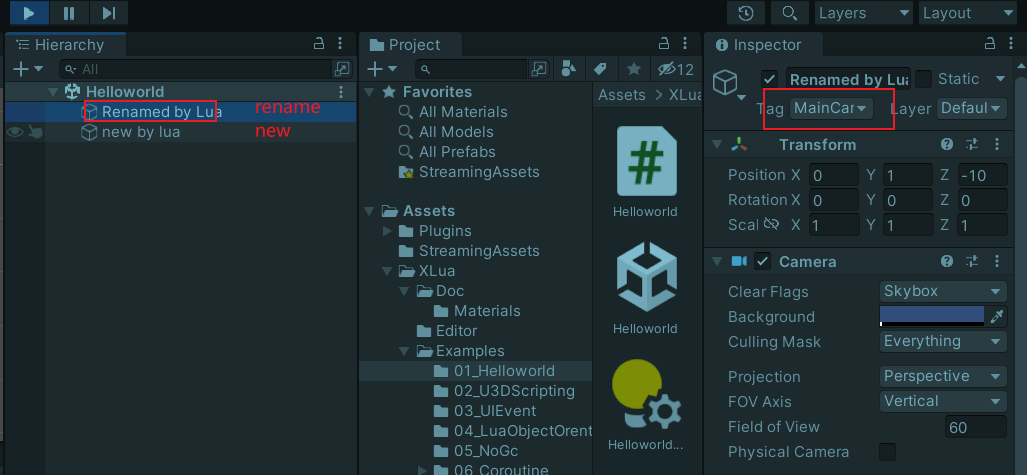
访问组件
local gameObject = CS.UnityEngine.GameObject;
local camera = gameObject.Find('Main Camera'); --查找
camera.name = 'Renamed by Lua'; --修改
两种形式 . & :
local cameraCom = camera:GetComponent("Camera")
local cameraCom = camera.GetComponent(camera,"Camera")--销毁
gameObject.Destory(cameraCom)
相关文章:

xlua游戏热更新(lua访问C#)
CS.UnityEngine静态方法访问unity虚拟机 创建游戏物体 CS.UnityEngine.GameObject(new by lua);静态属性 CS.UnityEngine.GameObject(new by lua); -- 创建 local camera CS.UnityEngine.GameObject.Find(Main Camera); --查找 camera.name Renamed by Lua;访问组件 loca…...

04-Spring中Bean的作用域
Bean的作用域 scope的属性值 属性值作用singleton默认单例prototype原型每调用一次getBean()方法则获取一个新的Bean对象 , 每次注入的时候都是新对象request一个请求对应一个Bean仅限于在WEB应用中使用 , 需要引入web的框架如SpringMvc(global) session一个会话对应一个Bean…...

xlua游戏热更新(C#访问lua)
xlua作为Unity资源热更新的重要解决方案api,在Tecent重多游戏中被采用,本文通过案例去讲解xlua代码结构层次。 /** Tencent is pleased to support the open source community by making xLua available.* Copyright (C) 2016 THL A29 Limited, a Tence…...
【数据结构】二叉树经典例题---<你真的掌握二叉树了吗?>(第一弹)
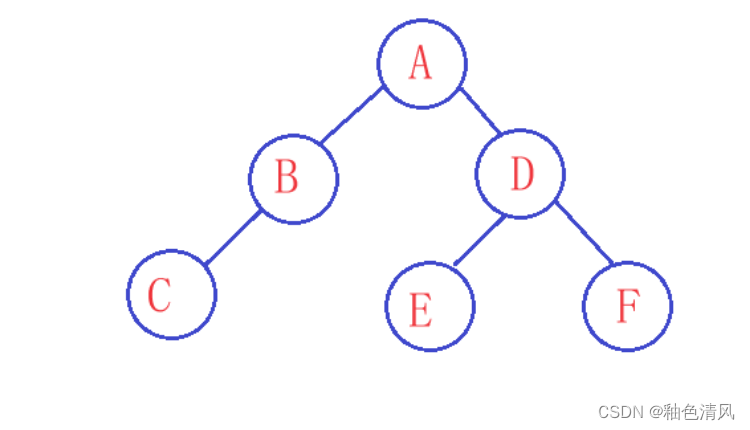
一、已知一颗二叉树如下图,试求: (1)该二叉树前序、中序和后序遍历的结果。 (2)该二叉树是否为满二叉树?是否为完全二叉树? (3)将它转换成对应的树或森林。 (4)这颗二叉树的深度为多少? (5)试对该二叉树进行前序线索化。 (6)试对…...
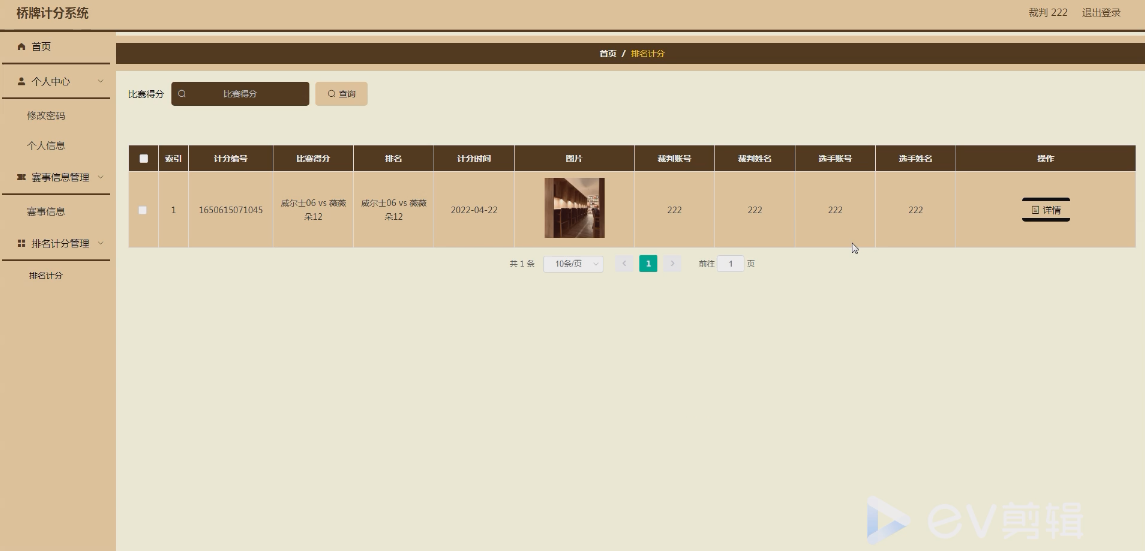
基于springboot实现桥牌计分管理系统项目【项目源码】
基于springboot实现桥牌计分管理系统演示 JAVA简介 JavaScript是一种网络脚本语言,广泛运用于web应用开发,可以用来添加网页的格式动态效果,该语言不用进行预编译就直接运行,可以直接嵌入HTML语言中,写成js语言&#…...
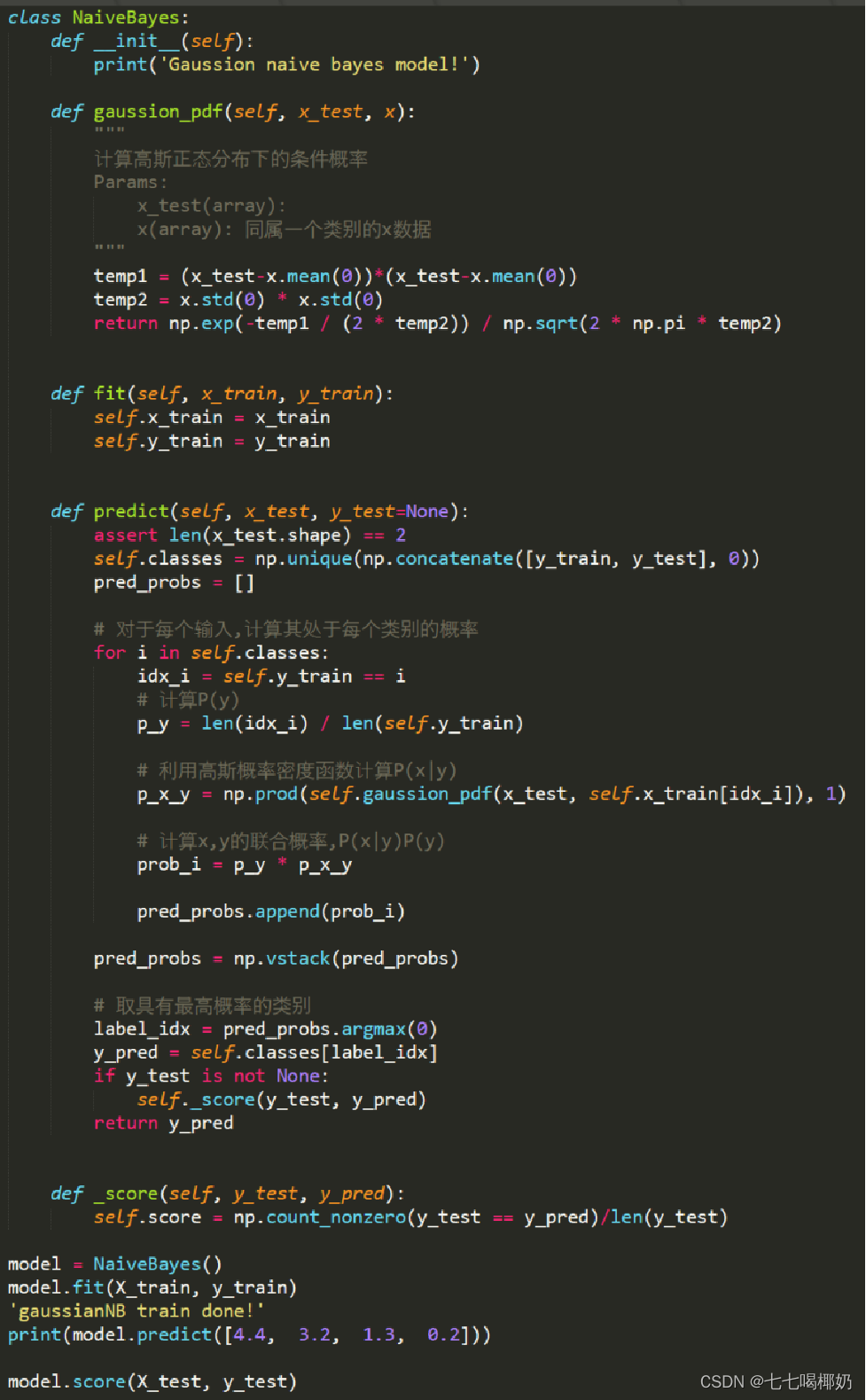
机器学习——朴素贝叶斯
目录 一、贝叶斯方法 背景知识 贝叶斯公式 二、朴素贝叶斯原理 判别模型和生成模型 1.朴素贝叶斯法是典型的生成学习方法 2.朴素贝叶斯法的基本假设是条件独立性 3.朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测 用于文…...

【PTE-day07 文件上传2】
1、常见的绕过方式 (1)畸形后缀名绕过 .php、.pht、.php3、.php4、.php5、.php2、.phtml、.pHp、.html、.Htm......(2)双写过滤字符绕过 (3).htaccess文件绕过 <FilesMatch "jpg"> SetHandler application/x-httpd-php...
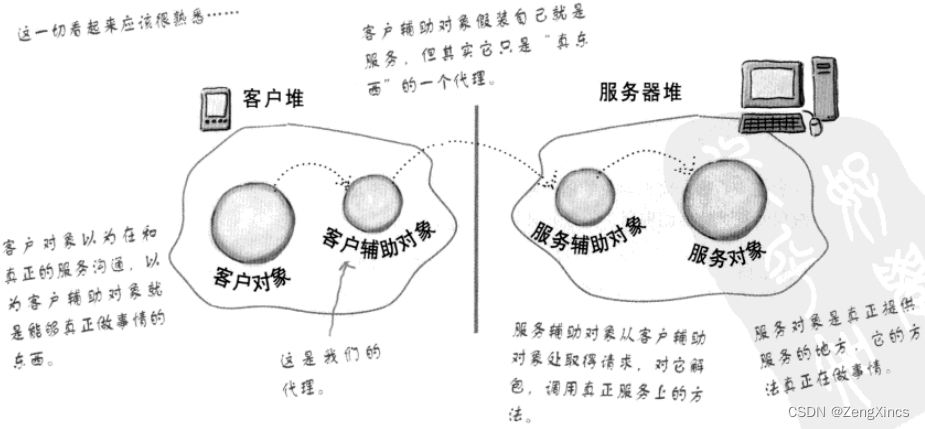
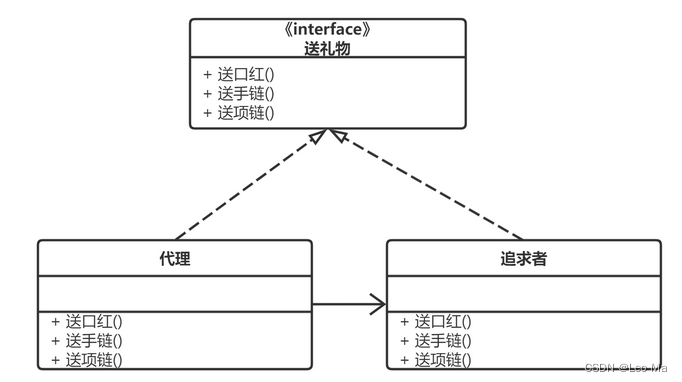
设计模式之十一:代理模式
代理可以控制和管理访问。 RMI提供了客户辅助对象和服务辅助对象,为客户辅助对象创建和服务对象相同的方法。RMI的好处在于你不必亲自写任何网络或I/O代码。客户程序调用远程方法就和运行在客户自己本地JVM对对象进行正常方法调用一样。 步骤一:制作远程…...

在spring boot中调用第三方接口时重试问题
文章目录 前言 spring-retry对第三方接口做重试,和处理操作 一、引入依赖 <!--重试请求的注解依赖--><dependency><groupId>org.springframework.retry</groupId><artifactId>spring-retry</artifactId></dependency>&l…...

记录一次多数据源配置失效的情况
说明:在一些复杂的业务情景,比如我们需要在一个订单审核通过后,在将数据库状态修改的同时,将订单与订单详细这两条数据写入到另一个数据库中。我们就可以通过在配置文件中,配置多数据源,然后通过在Mapper的…...

EasyExcel导出替换列中的变量
基于easyexcel2.0版本 easyexcel官网:https://easyexcel.opensource.alibaba.com/docs/2.x/quickstart/write 测试代码地址:https://gitee.com/wangtianwen1996/cento-practice/blob/master/src/test/java/com/xiaobai/easyexcel/DynamicHeadTest.java …...

机器人规划算法——将多边形障碍物离散到地图像素点上?
问题一:如何判断一个点是否在多边形区域内? 方法1:向量叉乘判别法 设多边形的顶点依次为A1,A2…An,要判断的点为P,那么分别计算向量PA1叉乘向量PA2,向量PA2叉乘向量PA3,…ÿ…...
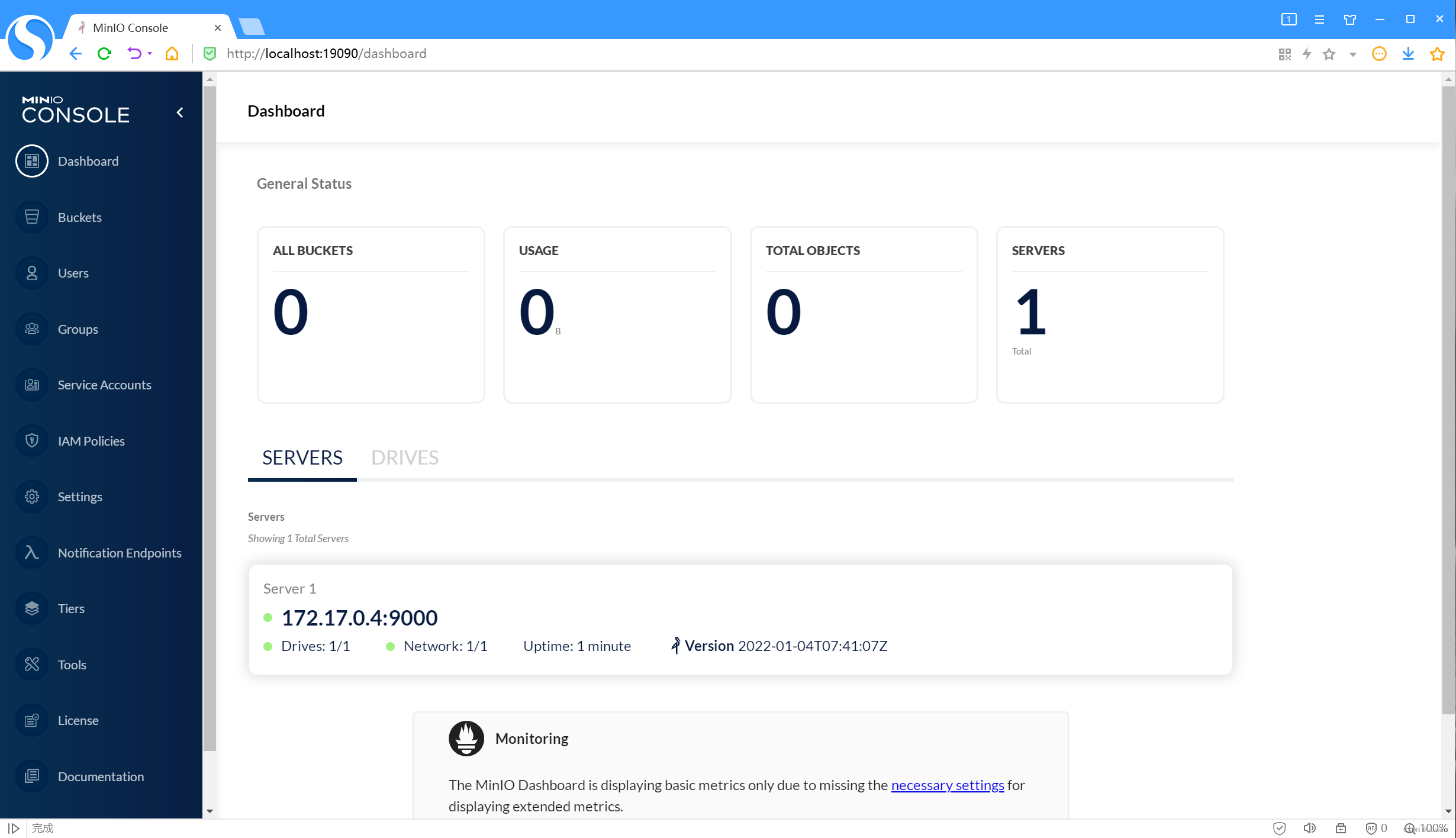
windows11使用docker部署安装minio
时间 2023-11-08 windows11使用docker部署安装minio 目录 1.docker 下载镜像2.docker安装镜像3.访问控制台4.安装问题解决5.使用教程 1.docker 下载镜像 调整镜像源到国内,否则会很慢 docker pull minio/minio2.docker安装镜像 设置用户名和密码时需要注意&…...

【JavaEESpring】Spring Web MVC⼊⻔
Spring Web MVC 1. 什么是 Spring Web MVC1.1 什么是 MVC ?1.2 是什么 Spring MVC? 2. 学习 Spring MVC2.1 建立连接2.2 请求2.3 响应 3. 相关代码链接 1. 什么是 Spring Web MVC 官⽅对于 Spring MVC 的描述是这样的: 1.1 什么是 MVC ? MVC 是 Model View C…...
flutter逆向 ACTF native app
前言 算了一下好长时间没打过CTF了,前两天看到ACTF逆向有道flutter逆向题就过来玩玩啦,花了一个下午做完了.说来也巧,我给DASCTF十月赛出的逆向题其中一道也是flutter,不过那题我难度降的相当之低啦,不知道有多少人做出来了呢~ 还原函数名 flutter逆向的一大难点就是不知道l…...
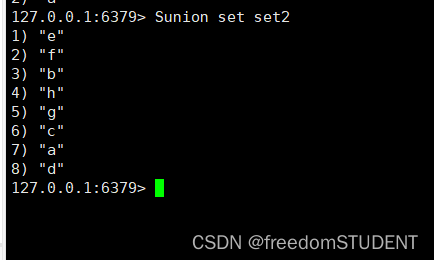
【Redis】set 集合
上一篇:list 列表 https://blog.csdn.net/m0_67930426/article/details/134364315?spm1001.2014.3001.5501 目录 Sadd Smembers Sismember Scard Srem 编辑Srandomember Spop Smove 集合类 Sdiff Sinter Sunion 官网 https://redis.io/commands/?…...
【算法与设计模式】
一、数据结构与算法 1、算法性能评估 时间复杂度、空间复杂度 2、数据结构 数组与列表 队列 堆栈 链表 二叉树 多叉树 递归算法 二、设计模式 1、单例 (1)GIL:线程互斥锁。保证同一时刻只有一个线程在进行。 (2)…...

Javaweb之javascript的小案例的详细解析
1.5.4 案例 1.5.4.1 需求说明 鲁迅说的好,光说不练假把式,光练不说傻把式。所以接下来我们需要通过案例来加强对于上述DOM知识的掌握。需求如下3个: 点亮灯泡 将所有的div标签的标签体内容后面加上:very good 使所有的复选框呈现被选中的…...
Vant 移动端UI 组件自动引入
Vue项目中安装Vant # Vue 3 项目,安装最新版 Vant npm i vant 组件按需引入配置 Vant按需引入- - -安装:unplugin-vue-components 插件 unplugin-vue-components 插件可以在Vue文件中自动引入组件(包括项目自身的组件和各种组件库中的组件&…...
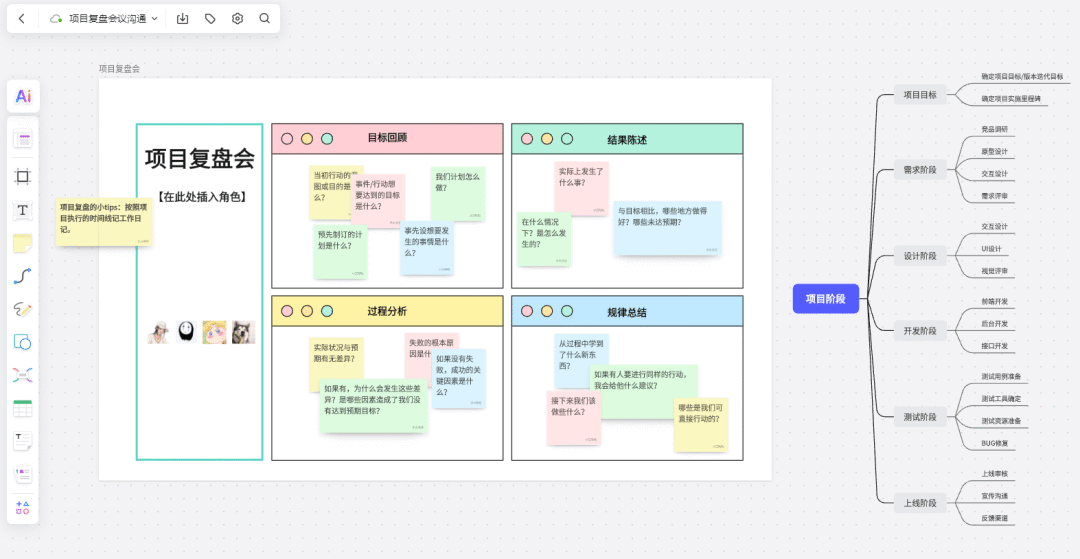
敏捷开发是什么?敏捷开发流程是怎么样的?
1. 什么是敏捷开发? 敏捷开发是一种迭代、增量式的软件开发方法,旨在通过灵活、协作和快速响应变化的方式,提高开发团队的效率和产品的质量。相较于传统的瀑布式开发模型,敏捷开发更加注重用户需求的响应和团队协作࿰…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
