自动控制原理--面试问答题
以下文中的,例如 s_1 为 s下角标1。面试加油!
- 控制系统的三要素:稳准快。稳,系统最后不能震荡、发散,一定要收敛于某一个值;快,能够迅速达到系统的预设值;准,最后稳态值和预设值的差比较小。
- 简要介绍身边的反馈系统:温度控制系统,温室大棚,锅炉是执行器件产生热量,传感器实时监测温度并反馈到控制器中,经过运算若低于温度则锅炉持续升热,反之同样。
- 控制系统的数学模型:在时域上可以用微分方程,在频域在复频域上用传递函数,方框图、信号流图。
- 传递函数是什么:在零初始条件下(系统没有储能的情况下,系统的输出信号完全由系统的输入信号引起),系统的输出拉氏变换比上输入的拉氏变换即为传递函数。
- 惯性系统(一阶系统)有哪些参数,分别作用是啥:只有一个参数,时间常数T,对于一阶系统可以调节快速性和稳定性。一阶系统没有超调量。看T的时间常数大小来判断快速性,T越大,快速性越差。
- 二阶系统有哪些时域的指标参数,分别定义和作用是啥:(1)延迟时间 t d :指输出响应第一次达到稳态值50%所需的时间。(2)上升时间 t_r :指输出响应第一次上升到稳态值所需要的时间。对于欠阻尼二阶系统,通常采用由0上升到稳态值的100%所需的时间;对于过阻尼系统,通常采用由稳态值的10%上升到稳态值的90%所需的时间。(3)峰值时间 t_p :指输出响应超过稳态值而达到第一个峰值 c{max}=c(t_ p) 所需的时间。(4)调节时间(或称过渡过程时间) t _s :指当c(t)和c(∞)之间误差达到规定允许范围(c(∞)的±5%或±2%),并且以后不再超出此范围所需的最小时间。(5)最大超调量(简称超调量) σ_p :系统响应的最大偏离量与终值的差与终值比的百分数。
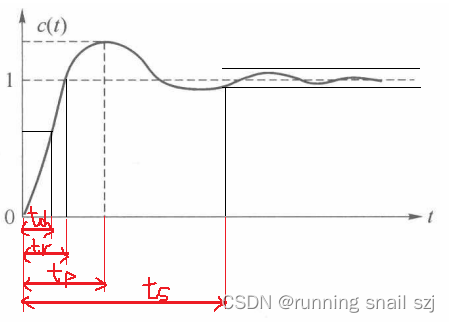
- 二阶系统的阻尼比、无阻尼自振角频率对常见指标的影响:典型二阶系统——弹簧阻尼系统分析。
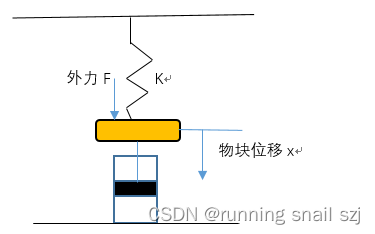
Wn为无阻尼振荡频率,反应弹簧的劲度系数,Wd为阻尼振荡频率,阻尼比反应阻尼系数与劲度系数的关系。Wn一定时:
阻尼比 ξ<0 的二阶系统是不稳定的,系统的动态过程为发散正弦震荡或单调发散的形式;
阻尼比 ξ=0 ,则特征方程有一对纯虚根,s_1,2=±jω_n,对应于s平面虚轴上一对共轭极点,可以算出系统的阶跃响应为等幅振荡,此时系统为无阻尼情况;
阻尼比 0<ξ<1 ,则特征方程有一对具有负实部的共轭复根,s_1,2=-ξω_n±jω_n √(1-ξ^2 ),对应于s平面左半部分的共轭复数极点,相应的阶跃相应为衰减震荡过程,系统为欠阻尼情况;
阻尼比 ξ=1 ,则特征方程有两个相等的负实根,s_1,2=-ω_n,对应于s平面负实轴上的两个相等实极点,相应的阶跃响应非周期地趋于稳态输出,此时系统为临界阻尼情况;
阻尼比 1<ξ ,则特征方程有两个不相等的负实根,s_1,2=-ξω_n±ω_n √(ξ^2-1),对应于s平面负实轴上的两个不等实极点,相应的单位阶跃响应也是非周期地趋于稳态输出,但响应速度比临界阻尼情况缓慢,因此称为过阻尼状态。
可以通过这个例子,阻尼越大弹簧越不震荡,容易得出:阻尼ξ和阻尼振荡频率Wd越大,上升时间、调节时间、峰值时间、超调量都越小;峰值时间等于阻尼振荡周期的一半,t=Π/Wd,与阻尼ξ无关;超调量只与阻尼比有关。 - 高阶系统的等效,如何分析一个高阶系统,也即如何找到高阶系统的主导极点?:找到最能影响系统性能的极点,然后近似当成二阶系统来对待。闭环主导极点为距离虚轴最近的闭环极点。拉普拉斯变换,拉普拉斯的衰减因子e^(-δt),δ越大经过相同时间衰减的越少 。
- 稳定性判据有哪些:分为时域和频域回答。时域:劳斯稳定判据(判断系统特征根是否全部位于s左半平面,有全0行就用上一行系数构造辅助方程并对s求导,得到的系数替代得到完整的劳斯计算表)、赫尔维兹稳定性判据。频域:奈奎斯特稳定性判据、对数稳定性判据。 频域先省略后补
- 稳态误差,要想使二型系统的稳态误差输出为常数,则输入信号满足什么条件:先分系统类型,再用终值定理法计算。。。。。。。。
相关文章:

自动控制原理--面试问答题
以下文中的,例如 s_1 为 s下角标1。面试加油! 控制系统的三要素:稳准快。稳,系统最后不能震荡、发散,一定要收敛于某一个值;快,能够迅速达到系统的预设值;准,最后稳态值…...

Word2Vec的缺点
Word2Vec虽然非常强大,但也有一些明显的缺点: 无法处理多义词:Word2Vec会为每个单词分配一个唯一的词向量,这意味着它不能处理具有多种含义的单词。例如,“苹果”可以指一种水果,也可以指一个公司ÿ…...

vue如何解决跨域?原理?
Vue.js本身并不直接解决跨域问题,而是依赖于浏览器的同源策略。但是,Vue提供了一些方法来帮助我们解决跨域问题。 原理: 浏览器的同源策略规定,不同源(协议、域名、端口)之间的网络请求受到限制ÿ…...
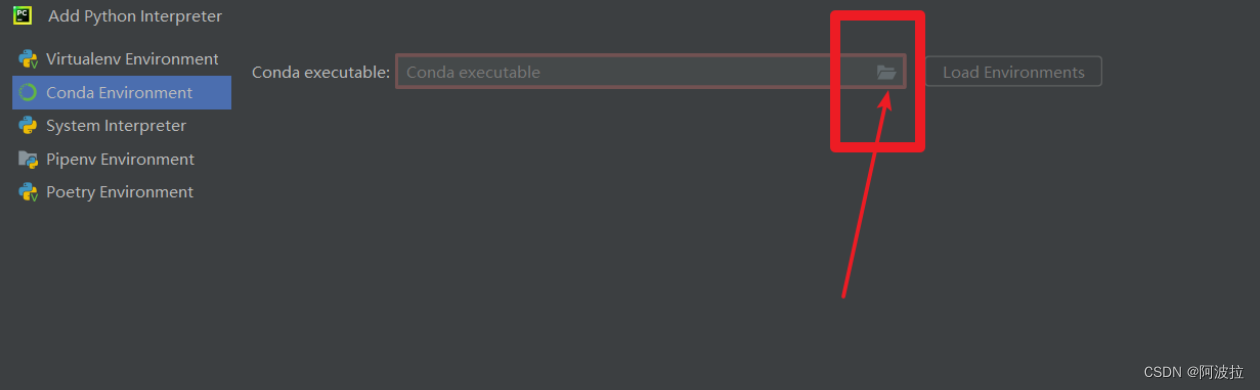
Conda executable is not found 三种问题解决
如果在PyCharm中配置Python解释器时显示“conda executable is not found”错误消息,这意味着PyCharm无法找到您的Conda可执行文件。您可以按照以下步骤解决此问题: 1.方法一 确认Conda已正确安装。请确保您已经正确安装了Anaconda或Minicondaÿ…...
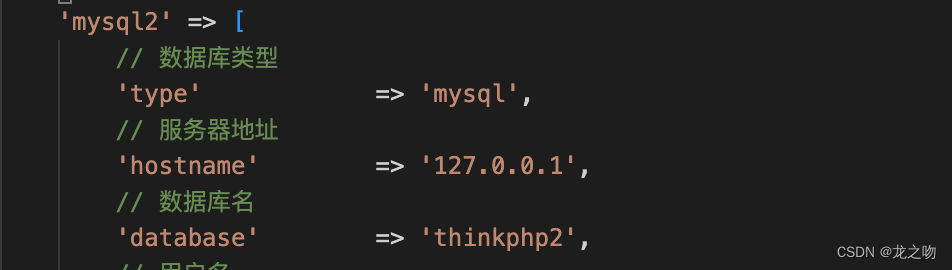
Thinkphp8 - 连接多个数据库
// 数据库连接配置信息connections > [mysql > [// 数据库类型type > mysql,// 服务器地址hostname > 127.0.0.1,// 数据库名database > thinkphp,// 用户名username > env(DB_USER, root),// 密码password >…...
Linux如何修改主机名(hostname)(亲测可用)
文章目录 背景Linux如何修改主机名(hostname)方法方法1. 使用 hostnamectl 命令示例 2. 编辑 /etc/hostname 文件注意事项 背景 我创建虚拟机的时候没设置主机名,现在显示localhost,有点尴尬😅: 需要重新设…...
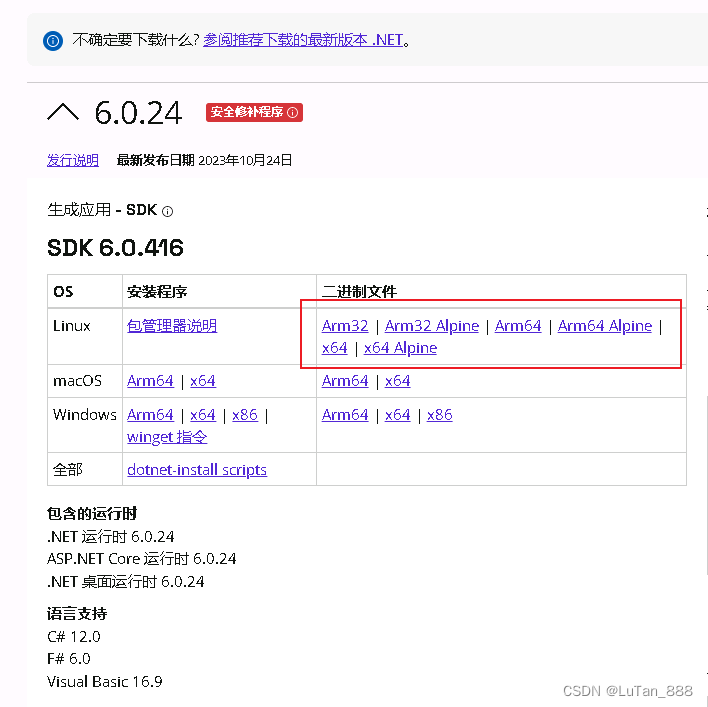
银河麒麟等 Linux系统 安装 .net 3.1,net 6及更高版本的方法
确定 系统的版本。华为鲲鹏处理器是 Arm64位的。 于是到windows 官网下载对应版本 .net sdk 下载地址 https://dotnet.microsoft.com/zh-cn/download/dotnet 2.下载完成后,再linux 服务器 上进入到文件所在目录,建议全英文路径。 然后依次输入以下命令 …...

Unity 使用INI文件存储数据或配置参数预设
法1:调用外部Capi库 具体使用: public class Ini{//读取INI文件需要调用C的APP[System.Runtime.InteropServices.DllImport("kernel32")]private static extern long WritePrivateProfileString(string section, string key, string val, st…...
clouldcompare工具使用
文章目录 1.界面1.1 布局1.3 视觉显示方向1.4 放大镜1.5 建立旋转中心2.快速入门2.1 剪裁2.2 多点云拼接 1.界面 1.1 布局 参考:https://blog.csdn.net/lovely_yoshino/article/details/129595201 1.3 视觉显示方向 1.4 放大镜 1.5 建立旋转中心 2.快速入门 2.1 …...
在vue3中使用Element-plus的图标
首先安装Element-Plus-icon # 选择一个你喜欢的包管理器# NPM $ npm install element-plus/icons-vue # Yarn $ yarn add element-plus/icons-vue # pnpm $ pnpm install element-plus/icons-vue 如何使用 Element-Plus-icon官方文档链接Icon 图标 | Element Plus (element-…...
图扑智慧农业:农林牧数据可视化监控平台
数字农业是一种现代农业方式,它将信息作为农业生产的重要元素,并利用现代信息技术进行农业生产过程的实时可视化、数字化设计和信息化管理。能将信息技术与农业生产的各个环节有机融合,对于改造传统农业和改变农业生产方式具有重要意义。 图…...
)
js 加解密 jsencrypt(非对称加密 rsa)
这是一个非对称加密的库,可以进行 rsa 加解密 使用方法 安装 npm install jsencrypt --save jsencrypt rsa 加解密 let rsaStr "这就是一个RSA加密的测试";let jsencryptObj new jsencrypt();jsencryptObj.getKey(); //这个方法用来生成一个密钥对…...
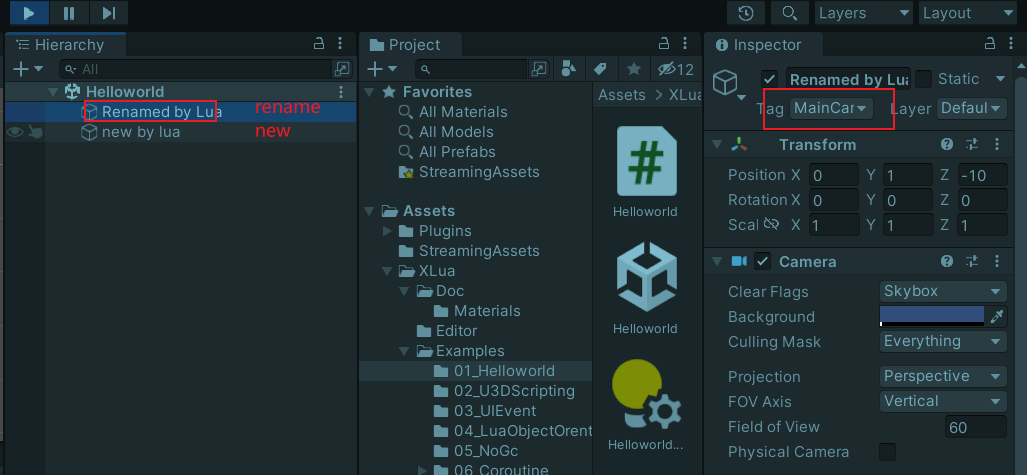
xlua游戏热更新(lua访问C#)
CS.UnityEngine静态方法访问unity虚拟机 创建游戏物体 CS.UnityEngine.GameObject(new by lua);静态属性 CS.UnityEngine.GameObject(new by lua); -- 创建 local camera CS.UnityEngine.GameObject.Find(Main Camera); --查找 camera.name Renamed by Lua;访问组件 loca…...

04-Spring中Bean的作用域
Bean的作用域 scope的属性值 属性值作用singleton默认单例prototype原型每调用一次getBean()方法则获取一个新的Bean对象 , 每次注入的时候都是新对象request一个请求对应一个Bean仅限于在WEB应用中使用 , 需要引入web的框架如SpringMvc(global) session一个会话对应一个Bean…...

xlua游戏热更新(C#访问lua)
xlua作为Unity资源热更新的重要解决方案api,在Tecent重多游戏中被采用,本文通过案例去讲解xlua代码结构层次。 /** Tencent is pleased to support the open source community by making xLua available.* Copyright (C) 2016 THL A29 Limited, a Tence…...
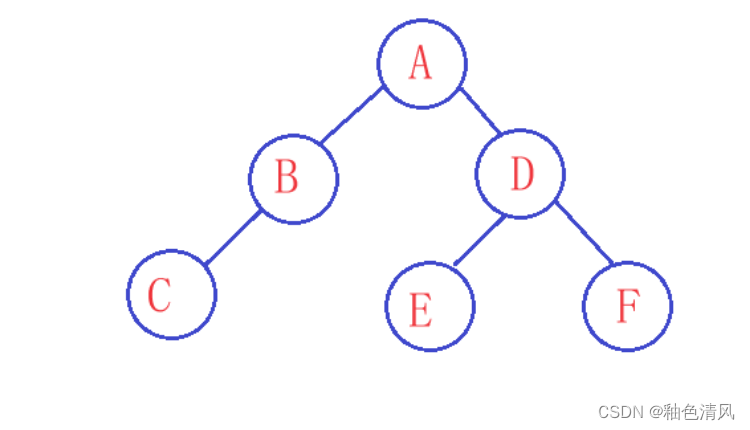
【数据结构】二叉树经典例题---<你真的掌握二叉树了吗?>(第一弹)
一、已知一颗二叉树如下图,试求: (1)该二叉树前序、中序和后序遍历的结果。 (2)该二叉树是否为满二叉树?是否为完全二叉树? (3)将它转换成对应的树或森林。 (4)这颗二叉树的深度为多少? (5)试对该二叉树进行前序线索化。 (6)试对…...
基于springboot实现桥牌计分管理系统项目【项目源码】
基于springboot实现桥牌计分管理系统演示 JAVA简介 JavaScript是一种网络脚本语言,广泛运用于web应用开发,可以用来添加网页的格式动态效果,该语言不用进行预编译就直接运行,可以直接嵌入HTML语言中,写成js语言&#…...
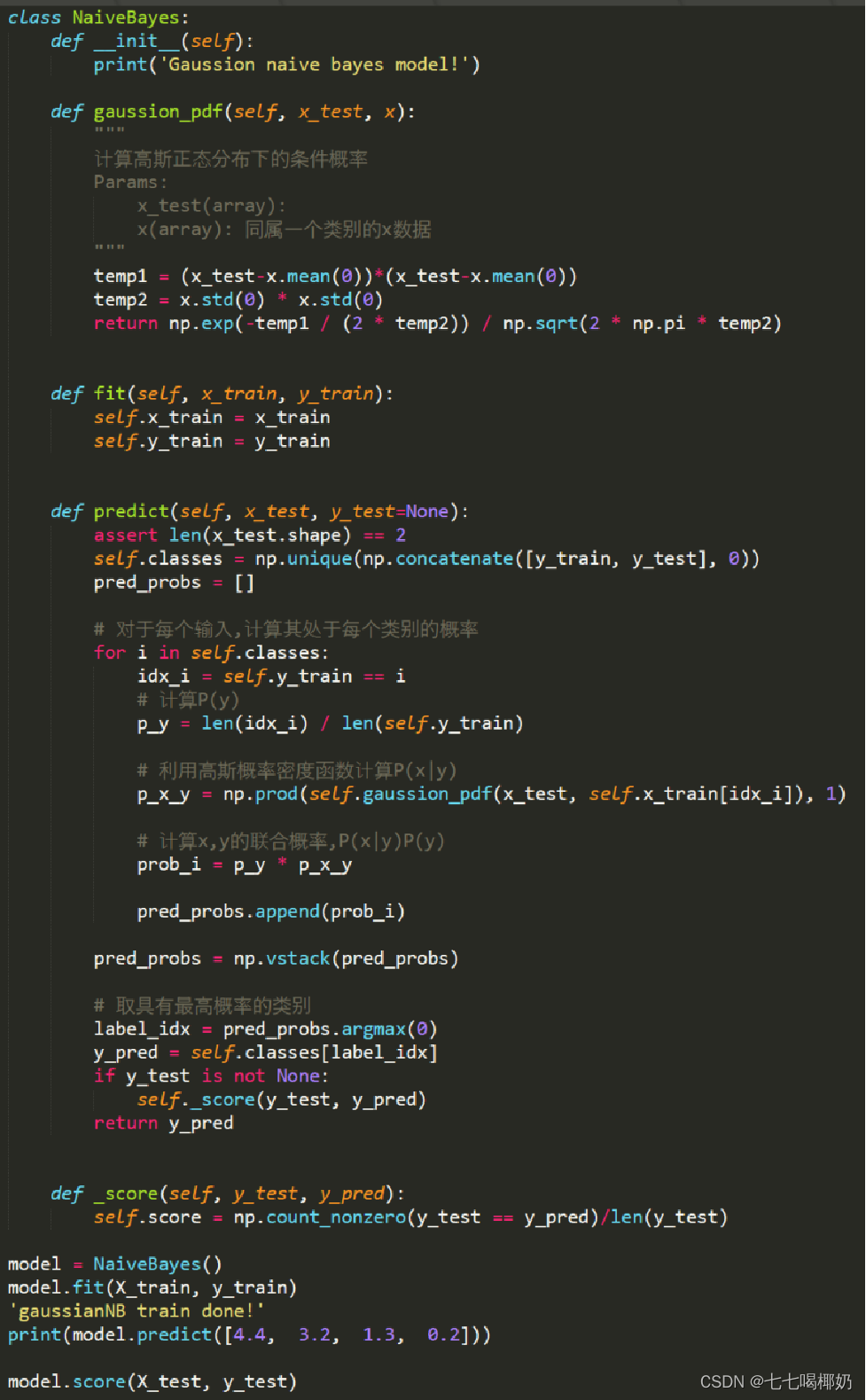
机器学习——朴素贝叶斯
目录 一、贝叶斯方法 背景知识 贝叶斯公式 二、朴素贝叶斯原理 判别模型和生成模型 1.朴素贝叶斯法是典型的生成学习方法 2.朴素贝叶斯法的基本假设是条件独立性 3.朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测 用于文…...

【PTE-day07 文件上传2】
1、常见的绕过方式 (1)畸形后缀名绕过 .php、.pht、.php3、.php4、.php5、.php2、.phtml、.pHp、.html、.Htm......(2)双写过滤字符绕过 (3).htaccess文件绕过 <FilesMatch "jpg"> SetHandler application/x-httpd-php...
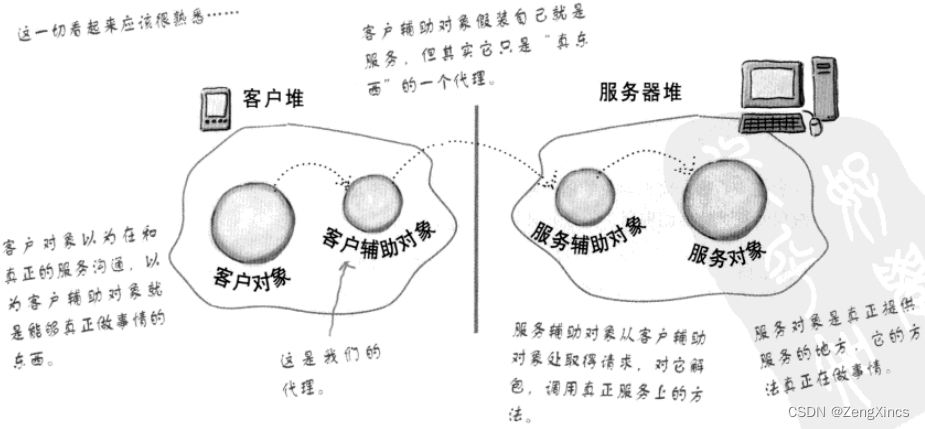
设计模式之十一:代理模式
代理可以控制和管理访问。 RMI提供了客户辅助对象和服务辅助对象,为客户辅助对象创建和服务对象相同的方法。RMI的好处在于你不必亲自写任何网络或I/O代码。客户程序调用远程方法就和运行在客户自己本地JVM对对象进行正常方法调用一样。 步骤一:制作远程…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...
