【数据结构】树与二叉树(十二):二叉树的递归创建(算法CBT)
文章目录
- 5.2.1 二叉树
- 5.2.2 二叉树顺序存储
- 5.2.3 二叉树链接存储
- 5.2.4 二叉树的遍历
- 1-3 先序、中序、后序遍历递归实现及相关练习
- 4. 中序遍历非递归
- 5. 后序遍历非递归
- 6. 先序遍历非递归
- 7. 层次遍历
- 5.2.5 二叉树的创建
- 先序创建
- a. 算法CBT
- b. 代码实现
- 代码整合
5.2.1 二叉树
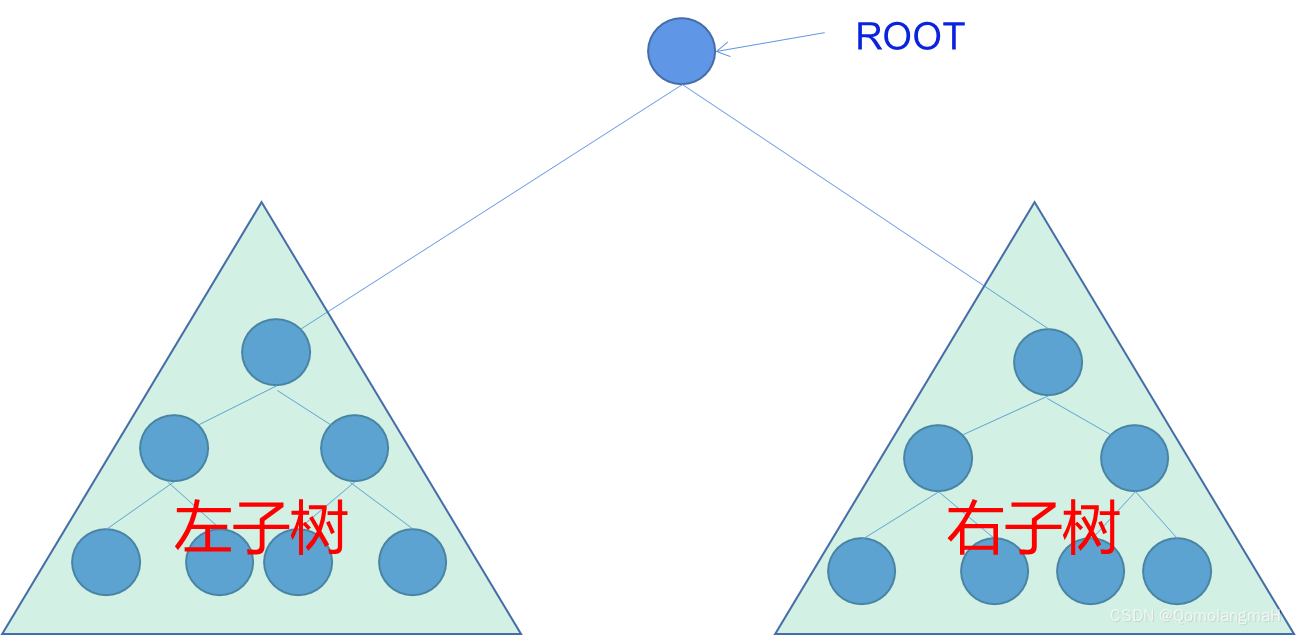
二叉树是一种常见的树状数据结构,它由结点的有限集合组成。一个二叉树要么是空集,被称为空二叉树,要么由一个根结点和两棵不相交的子树组成,分别称为左子树和右子树。每个结点最多有两个子结点,分别称为左子结点和右子结点。
二叉树性质
引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。
引理5.2:高度为k的二叉树中至多有 2 k + 1 − 1 2^{k+1}-1 2k+1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。
引理5.3:设T是由n个结点构成的二叉树,其中叶结点个数为 n 0 n_0 n0,度数为2的结点个数为 n 2 n_2 n2,则有 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1。
- 详细证明过程见前文:【数据结构】树与二叉树(三):二叉树的定义、特点、性质及相关证明
满二叉树、完全二叉树定义、特点及相关证明
- 详细证明过程见前文:【数据结构】树与二叉树(四):满二叉树、完全二叉树及其性质
5.2.2 二叉树顺序存储
二叉树的顺序存储是指将二叉树中所有结点按层次顺序存放在一块地址连续的存储空间中,详见:
【数据结构】树与二叉树(五):二叉树的顺序存储(初始化,插入结点,获取父节点、左右子节点等)
5.2.3 二叉树链接存储
二叉树的链接存储系指二叉树诸结点被随机存放在内存空间中,结点之间的关系用指针说明。在链式存储中,每个二叉树结点都包含三个域:数据域(Data)、左指针域(Left)和右指针域(Right),用于存储结点的信息和指向子结点的指针,详见:
【数据结构】树与二叉树(六):二叉树的链式存储
5.2.4 二叉树的遍历
- 遍历(Traversal)是对二叉树中所有节点按照一定顺序进行访问的过程。
- 通过遍历,可以访问树中的每个节点,并按照特定的顺序对它们进行处理。
- 对二叉树的一次完整遍历,可给出树中结点的一种线性排序。
- 在二叉树中,常用的遍历方式有三种:先序遍历、中序遍历和后序遍历。
- 这三种遍历方式都可以递归地进行,它们的区别在于节点的访问顺序。
- 在实现遍历算法时,需要考虑递归终止条件和递归调用的顺序。
- 还可以使用迭代的方式来实现遍历算法,使用栈或队列等数据结构来辅助实现。
- 遍历是二叉树中基础而重要的操作,它为其他许多操作提供了基础,如搜索、插入、删除等。
1-3 先序、中序、后序遍历递归实现及相关练习
【数据结构】树与二叉树(七):二叉树的遍历(先序、中序、后序及其C语言实现)
4. 中序遍历非递归
【数据结构】树与二叉树(八):二叉树的中序遍历(非递归算法NIO)
5. 后序遍历非递归
【数据结构】树与二叉树(九):二叉树的后序遍历(非递归算法NPO)
6. 先序遍历非递归
【数据结构】树与二叉树(十):二叉树的先序遍历(非递归算法NPO)
7. 层次遍历
【数据结构】树与二叉树(十一):二叉树的层次遍历(算法LevelOrder)
5.2.5 二叉树的创建
- 先序遍历
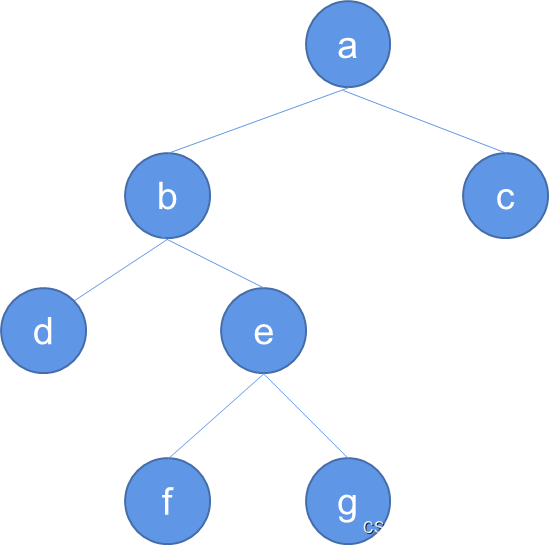
- a b d e f g c
- 中序遍历
- d b f e g a c
- 后序遍历
- d f g e b c a
- 层次遍历
- a b c d e f g
先序创建
由二叉树的遍历,很容易想到用遍历方法去创建二叉树。我们考虑从先根遍历思想出发来构造二叉树。
方法:输入当前被创建结点的数据域的值,如果不空,申请空间用指针指向,然后对数据域进行赋值,再递归对该结点的左右指针域进行赋值,这就是先根创建过程。当输入为空,则算法返回一个空指针(即空树。递归出口)。
a. 算法CBT

b. 代码实现
struct Node* CBT(char data[], int* index, char tostop) {char ch = data[(*index)++];if (ch == tostop) {return NULL;} else {struct Node* t = createNode(ch); t->left = CBT(data, index, tostop);t->right = CBT(data, index, tostop);return t;}
}
代码整合
#include <stdio.h>
#include <stdlib.h>struct Node {char data;struct Node* left;struct Node* right;
};struct Node* createNode(char data) {struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));if (newNode == NULL) {printf("Memory allocation failed!\n");exit(1);}newNode->data = data;newNode->left = NULL;newNode->right = NULL;return newNode;
}struct Node* CBT(char data[], int* index, char tostop) {char ch = data[(*index)++];if (ch == tostop) {return NULL;} else {struct Node* t = createNode(ch); t->left = CBT(data, index, tostop);t->right = CBT(data, index, tostop);return t;}
}
void inorderTraversal(struct Node* root) {if (root != NULL) {inorderTraversal(root->left);printf("%c ", root->data);inorderTraversal(root->right);}
}// 创建队列
struct Queue {struct Node* node;struct Queue* next;
};// 初始化队列
void create(struct Queue** front, struct Queue** rear) {*front = *rear = NULL;
}// 入队列
void enqueue(struct Queue** front, struct Queue** rear, struct Node* node) {struct Queue* temp = (struct Queue*)malloc(sizeof(struct Queue));if (temp == NULL) {printf("Memory allocation failed!\n");exit(1);}temp->node = node;temp->next = NULL;if (*rear == NULL) {*front = *rear = temp;return;}(*rear)->next = temp;*rear = temp;
}// 出队列
void dequeue(struct Queue** front) {if (*front == NULL) {return;}struct Queue* temp = *front;*front = (*front)->next;free(temp);
}// 层次遍历二叉树
void levelOrder(struct Node* root) {if (root == NULL) {return;}struct Queue* front, * rear;create(&front, &rear);enqueue(&front, &rear, root);while (front != NULL) {struct Node* current = front->node;printf("%c ", current->data);if (current->left != NULL) {enqueue(&front, &rear, current->left);}if (current->right != NULL) {enqueue(&front, &rear, current->right);}dequeue(&front);}
}int main() {char tostop = '#';char input_data[] = {'a', 'b', 'd', '#', '#', 'e', 'f', '#', '#', 'g', '#', '#', 'c', '#', '#'};int index = 0;struct Node* root = CBT(input_data, &index, tostop);// 层次遍历二叉树printf("层次遍历二叉树: ");levelOrder(root);printf("\n");printf("中序遍历二叉树: ");inorderTraversal(root);printf("\n");return 0;
}
相关文章:

【数据结构】树与二叉树(十二):二叉树的递归创建(算法CBT)
文章目录 5.2.1 二叉树二叉树性质引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。引理5.2:高度为k的二叉树中至多有 2 k 1 − 1 2^{k1}-1 2k1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。引理5.3&…...

Qt绘制网格和曲线
绘制网格: void Widget::drawGrid(QPainter &p, QRect &windRect) {QRect rect(windRect.left()m_margins.left(),windRect.top()m_margins.top(),windRect.width()-m_margins.left()-m_margins.right(),windRect.height()-m_margins.top()-m_margins.bo…...

2023-11-12
今日比较摆烂, 但是把自写管道的原理搞懂了, 主要是把 exp 完完全全看懂了, 还不错. 然后就没干啥了. 明日计划: 学校的作业. AFL 源码. 我真是服了我自己了, AFL 源码搁多久了, 操操操 然后把 seccomp 重新学习下...

[工业自动化-16]:西门子S7-15xxx编程 - 软件编程 - 西门子仿真软件PLCSIM
目录 前言: 一、PLCSIM仿真软件 1.1 PLCSIM仿真软件基础版(内嵌) 1.2 PLCSIM仿真软件与PLCSIM仿真软件高级版的区别? 1.3 PLCSIM使用 前言: PLC集成开发环境是运行在Host主机上,Host主机与PLC可以通过…...

运行npm install卡住不动的几种解决方案
在前端开发经常会遇到运行npm install 来安装工具包一直卡住不动,为此这里提供几种解决方案,供大家参考学习,不足之处还请指正。 第一种方案、首先检查npm代理,是否已经使用国内镜像 // 执行以下命令查看是否为国内镜像 npm con…...
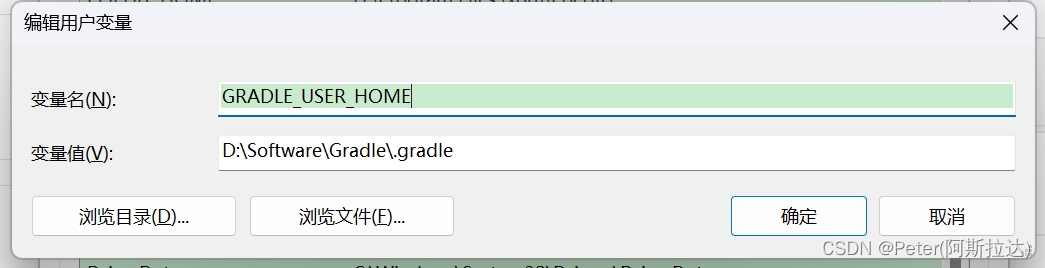
[Android]_[初级]_[配置gradle的环境变量设置安装位置]
场景 在开发Android项目的时候, gradle是官方指定的构建工具。不同项目通过wrapper指定不同版本的gradle。随着项目越来越多,使用的gradle版本也增多,导致它以来的各种库也增加,系统盘空间不足,怎么解决? 说明 grad…...
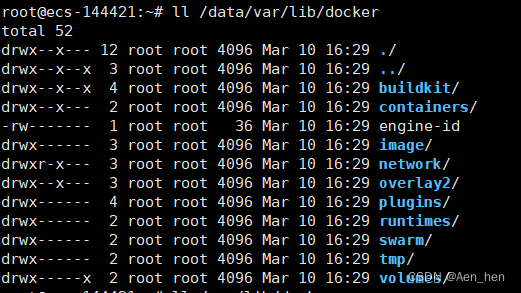
docker更改存储目录原因及方案
为什么一定要将docker的存储目录挂载到其他目录 docker在安装时默认存储目录在/var/lib/docker,而该目录是在系统盘下的。docker安装后,会使用各种各样的镜像,动辄几个G,那么如此多的镜像文件,装着装着系统盘就撑爆了…...
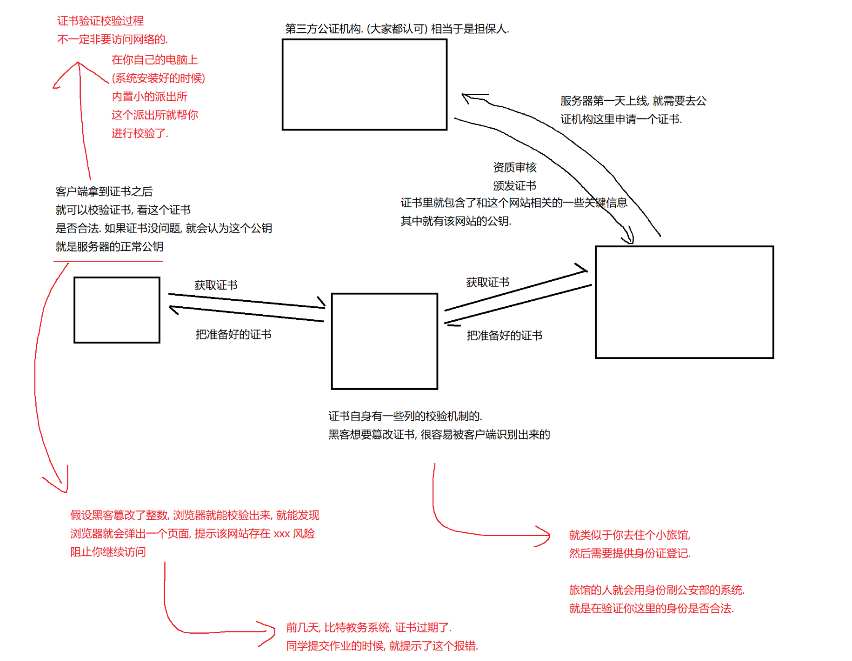
HTTPS的工作流程
. HTTPS是什么? https是应用层中的一个协议,是在http协议的基础上引入的一个加密层。 为什么需要HTTPS 由于http协议内容都是按照文本的方式明文传输的,这就导致传输过程中会出现一些被篡改的情况。运营商劫持事件最开始百度,…...

C++语言的广泛应用领域
目录 1. 系统级编程 2. 游戏开发 3. 嵌入式系统 4. 大数据处理 5. 金融和量化分析 6. 人工智能和机器学习 7. 网络和通信 结语 C是一种多范式编程语言,具有高性能、中级抽象能力和面向对象的特性。由Bjarne Stroustrup于1979年首次设计并实现,C在…...
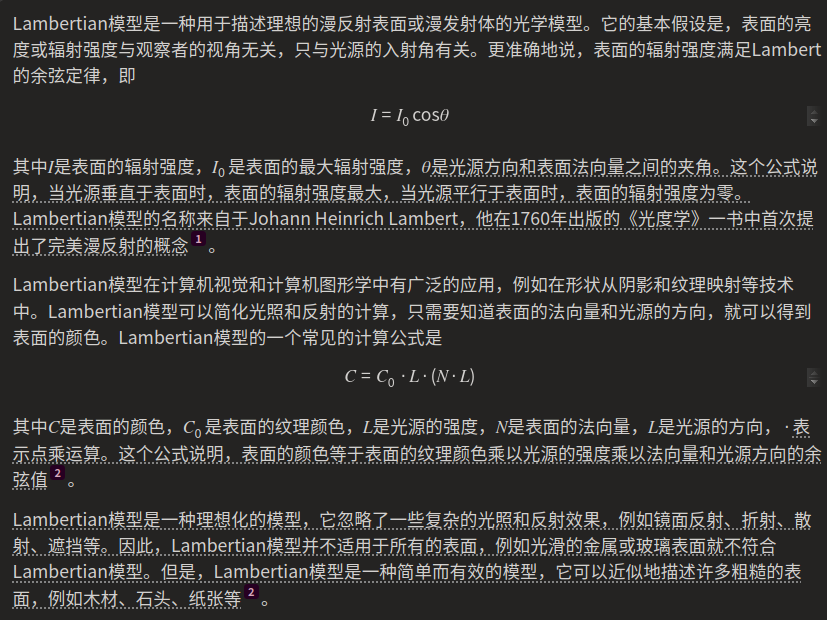
Lambertian模型(完美漫反射)
这里使用相乘的方式组合光照色和纹理色。根据这个模型,面朝光源的区域光照强度高,纹理色也相应增强。面背光源的区域光照弱,纹理色也被抑制。这样通过光照和纹理的结合,可以合成出具有照明效果的面部颜色,而不仅仅是固定的纹理本身的颜色。相乘方式可以近似实现不同光照方向下面…...

MATLAB的编程与应用,匿名函数、嵌套函数、蒙特卡洛法的掌握与使用
目录 1.匿名函数 1.1.匿名函数的定义与分类 1.2.匿名函数在积分和优化中应用 2.嵌套函数 2.1.嵌套函数的定义与分类 2.2.嵌套函数彼此调用关系 2.3.嵌套函数在积分和微分中应用 3.微分和积分 4.蒙特卡洛法 4.1.圆周率的模拟 4.2.计算N重积分(均匀分布&am…...
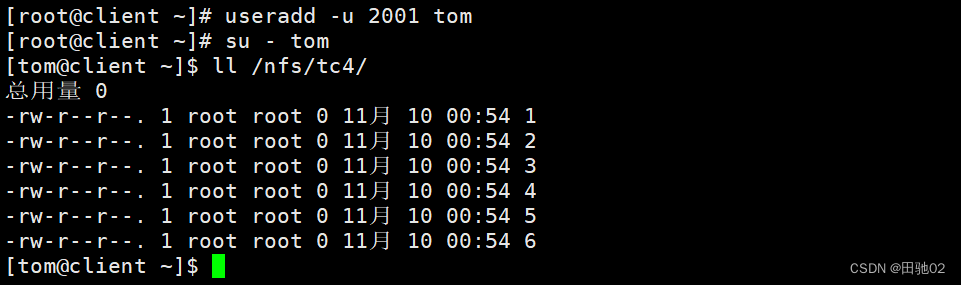
NFS服务器的搭建
架设一台NFS服务器,并按照以下要求配置 准备阶段:准备两台虚拟机,一台作为服务端,一台作为客户端 服务端(Server):192.168.75.139 客户端(Client):192.168.75.160 两…...

安卓Frida 常用脚本
打印调用堆栈, hook 某个方法,想看下调用堆栈,代码如下: function showStacks() {Java.perform(function () {send(Java.use("android.util.Log").getStackTraceString(Java.use("java.lang.Exception").$new()));});} 二,需要hook okhttp3 HttpUrl …...
机器学习数据预处理——Word2Vec的使用
引言: Word2Vec 是一种强大的词向量表示方法,通常通过训练神经网络来学习词汇中的词语嵌入。它可以捕捉词语之间的语义关系,对于许多自然语言处理任务,包括情感分析,都表现出色。 代码: 重点代码&#…...
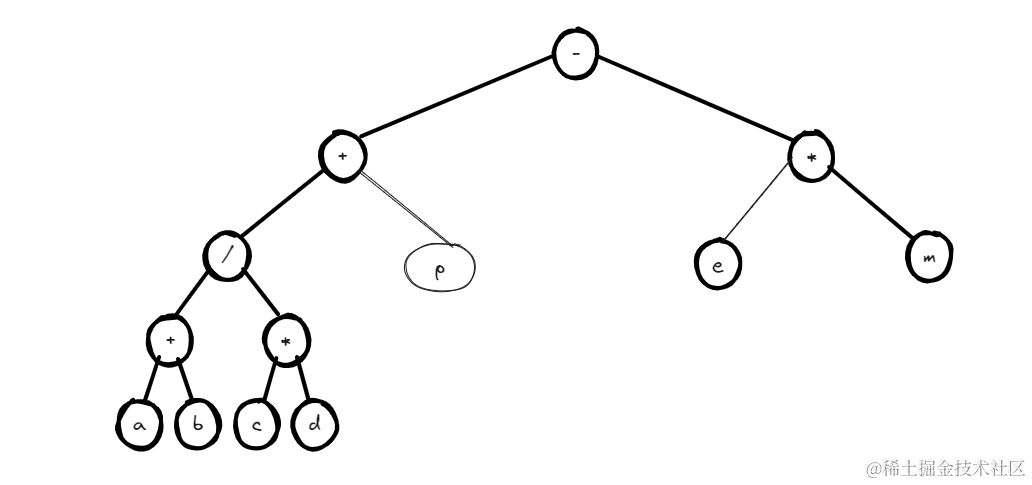
面试算法常考题之-------逆波兰式合集
逆波兰式背景介绍 逆波兰式是一种特殊的数学表达式表示法,它的诞生背景可以追溯到20世纪30年代。当时,波兰数学家Jan Wjtowicz和Wacław Sierpiński提出了一种新的数学表达式表示法,这种表示法将运算符放在操作数之后,而不是传统…...

独热编码和Word2Vec的区别
独热编码和Word2Vec都是自然语言处理中将词向量化的方式,但它们之间并没有直接的关系或依赖性。它们可以被视为在处理词向量时的两种不同方法或策略。 独热编码是一种简单直观的方法,每个词被表示为一个长向量,其中只有一个元素是1࿰…...

RestTemplate.postForEntity 方法进行 HTTP POST 请求
RestTemplate 是 Spring Framework 提供的一个用于处理 HTTP 请求的客户端工具。其中,postForEntity 是 RestTemplate 提供的用于发送 HTTP POST 请求并返回 ResponseEntity 对象的方法。 public <T> ResponseEntity<T> postForEntity(String url, Obj…...

盘点双11!阿里妈妈助这些品牌短视频赢增长!
刚刚!一年一度的双11落下帷幕,很多新变化值得回味。 尽管天气在变凉,但市场出现了逐渐回暖的迹象。在此背景下,大量商家特别关心如何在双11打一场漂亮的胜仗。 卖方如何行动,关键在于买方的变化。在阿里妈妈发布的《…...
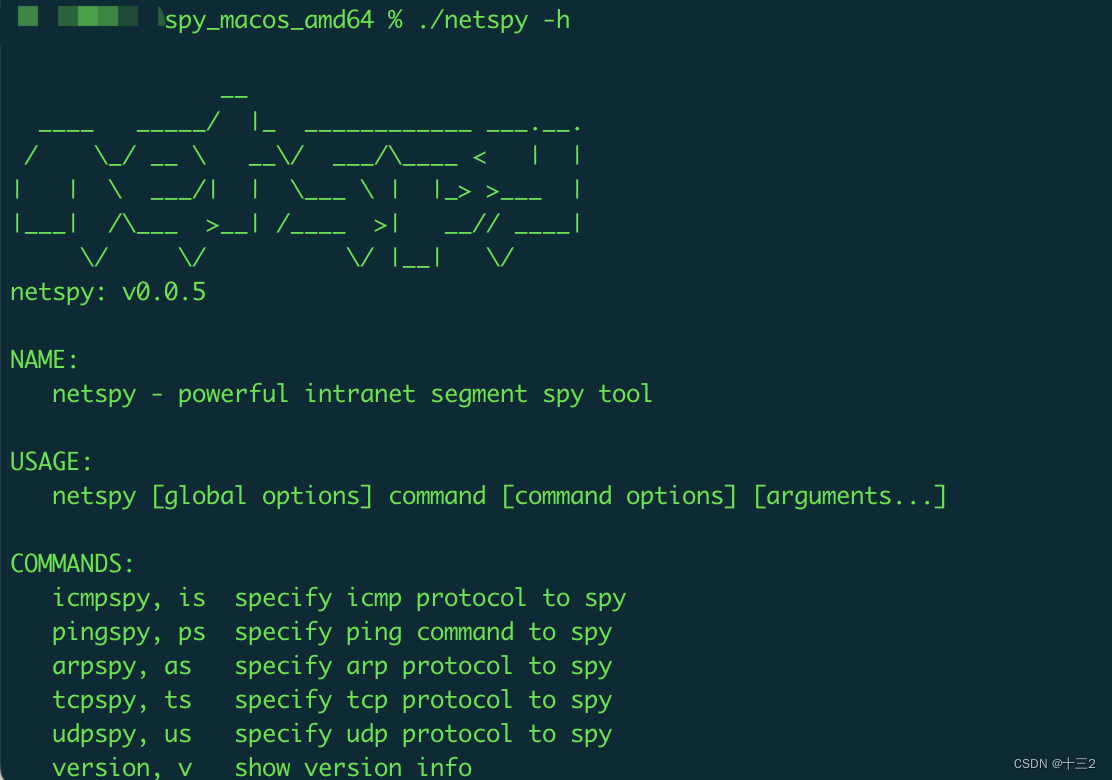
内网可达网段探测netspy- Mac环境
netspy是一款快速探测内网可达网段工具 当我们进入内网后想要扩大战果,那我们可能首先想知道当前主机能通哪些内网段。 netspy正是一款应用而生的小工具,体积较小,速度极快,支持跨平台,支持多种协议探测,…...

Liunx命令汇总
一.用户相关命令 1.1账号管理 创建用户: useradd (选项) 用户名用户口令: passwd (选项) 用户名修改用户: usermod 选项 用户名删除用户: userdel (选项) 用…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
