Qt绘制网格和曲线
绘制网格:
void Widget::drawGrid(QPainter &p, QRect &windRect)
{QRect rect(windRect.left()+m_margins.left(),windRect.top()+m_margins.top(),windRect.width()-m_margins.left()-m_margins.right(),windRect.height()-m_margins.top()-m_margins.bottom());if (!rect.isValid())return;QPen penDot(Qt::DotLine);penDot.setColor(Qt::gray);QPen penSolid(Qt::SolidLine);penSolid.setColor(Qt::black);
// pen.setColor(this->palette().light().color());p.setPen(penSolid);p.drawRect(rect.adjusted(0,0,-1,-1));int Xpos;qreal Xvalue;QString xlab;QFontMetrics textSize(this->font());QRect textRect;for(int i=0;i<=m_XTicks;i++){Xpos=rect.left()+i*m_xRatio; //Xvalue=m_xmin+i*m_xspan/m_XTicks;//p.setPen(penDot);p.drawLine(Xpos,rect.top(),Xpos,rect.bottom());p.setPen(penSolid);p.drawLine(Xpos,rect.bottom(),Xpos,rect.bottom()+5);xlab=QString::asprintf("%.1f",Xvalue);textRect=textSize.boundingRect(xlab);//得到字符串的rectp.drawText(Xpos-textRect.width()/2,rect.bottom()+5+textRect.height(),xlab);}xlab="time(sec)";textRect=textSize.boundingRect(xlab);//得到字符串的rectp.drawText(rect.left()+(rect.width()-textRect.width())/2,windRect.bottom()-textRect.height()/2,xlab);xlab="曲线绘图";textRect=textSize.boundingRect(xlab);//得到字符串的rectp.drawText(rect.left()+(rect.width()-textRect.width())/2,(m_margins.top()-textRect.height())/2+textRect.height(),xlab);int Ypos;qreal Yvalue;QString ylab;for(int i=0;i<=m_YTicks;i++){Ypos=rect.bottom()-i*m_yRatio; //Yvalue=m_ymin+i*m_yspan/m_YTicks;//p.setPen(penDot);p.drawLine(rect.left(),Ypos,rect.right(),Ypos);p.setPen(penSolid);p.drawLine(rect.left()-5,Ypos,rect.left(),Ypos);ylab=QString::asprintf("%.1f",Yvalue);textRect=textSize.boundingRect(ylab);//得到字符串的rectp.drawText(rect.left()-10-textRect.width(),Ypos+textRect.height()/2,ylab);}ylab="函数值";textRect=textSize.boundingRect(ylab);//得到字符串的rectp.save();p.translate(0,windRect.height()/2); //平移到左侧中心p.rotate(-90);//逆时针旋转90度,变成正北为X轴,正东为Y轴p.drawText(-textRect.width()/2,(m_margins.left()-textRect.height())/2,ylab);p.restore();
}绘制曲线:
void Widget::drawCurve(QPainter &p, QRect &windRect)
{QPolygon curve(m_points.count());for(int i=0;i<m_points.count();i++)curve[i]=m_points[i];QPen penSolid(Qt::SolidLine);penSolid.setColor(Qt::blue);penSolid.setWidth(2);p.setPen(penSolid);p.drawPolyline(curve);
}相关文章:

Qt绘制网格和曲线
绘制网格: void Widget::drawGrid(QPainter &p, QRect &windRect) {QRect rect(windRect.left()m_margins.left(),windRect.top()m_margins.top(),windRect.width()-m_margins.left()-m_margins.right(),windRect.height()-m_margins.top()-m_margins.bo…...

2023-11-12
今日比较摆烂, 但是把自写管道的原理搞懂了, 主要是把 exp 完完全全看懂了, 还不错. 然后就没干啥了. 明日计划: 学校的作业. AFL 源码. 我真是服了我自己了, AFL 源码搁多久了, 操操操 然后把 seccomp 重新学习下...

[工业自动化-16]:西门子S7-15xxx编程 - 软件编程 - 西门子仿真软件PLCSIM
目录 前言: 一、PLCSIM仿真软件 1.1 PLCSIM仿真软件基础版(内嵌) 1.2 PLCSIM仿真软件与PLCSIM仿真软件高级版的区别? 1.3 PLCSIM使用 前言: PLC集成开发环境是运行在Host主机上,Host主机与PLC可以通过…...

运行npm install卡住不动的几种解决方案
在前端开发经常会遇到运行npm install 来安装工具包一直卡住不动,为此这里提供几种解决方案,供大家参考学习,不足之处还请指正。 第一种方案、首先检查npm代理,是否已经使用国内镜像 // 执行以下命令查看是否为国内镜像 npm con…...
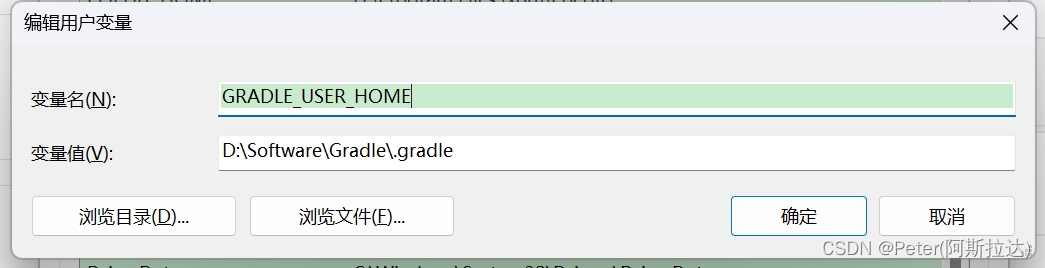
[Android]_[初级]_[配置gradle的环境变量设置安装位置]
场景 在开发Android项目的时候, gradle是官方指定的构建工具。不同项目通过wrapper指定不同版本的gradle。随着项目越来越多,使用的gradle版本也增多,导致它以来的各种库也增加,系统盘空间不足,怎么解决? 说明 grad…...
docker更改存储目录原因及方案
为什么一定要将docker的存储目录挂载到其他目录 docker在安装时默认存储目录在/var/lib/docker,而该目录是在系统盘下的。docker安装后,会使用各种各样的镜像,动辄几个G,那么如此多的镜像文件,装着装着系统盘就撑爆了…...
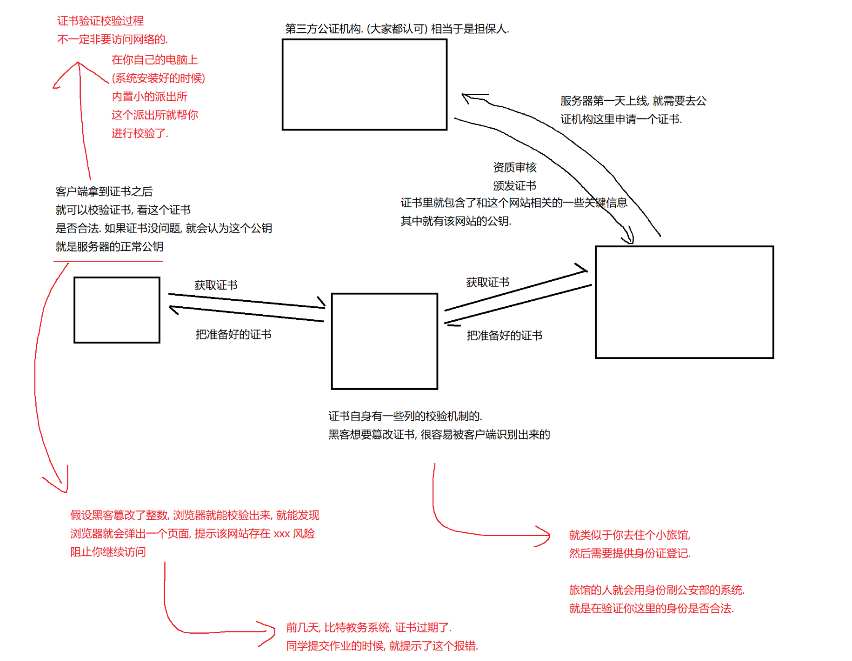
HTTPS的工作流程
. HTTPS是什么? https是应用层中的一个协议,是在http协议的基础上引入的一个加密层。 为什么需要HTTPS 由于http协议内容都是按照文本的方式明文传输的,这就导致传输过程中会出现一些被篡改的情况。运营商劫持事件最开始百度,…...

C++语言的广泛应用领域
目录 1. 系统级编程 2. 游戏开发 3. 嵌入式系统 4. 大数据处理 5. 金融和量化分析 6. 人工智能和机器学习 7. 网络和通信 结语 C是一种多范式编程语言,具有高性能、中级抽象能力和面向对象的特性。由Bjarne Stroustrup于1979年首次设计并实现,C在…...
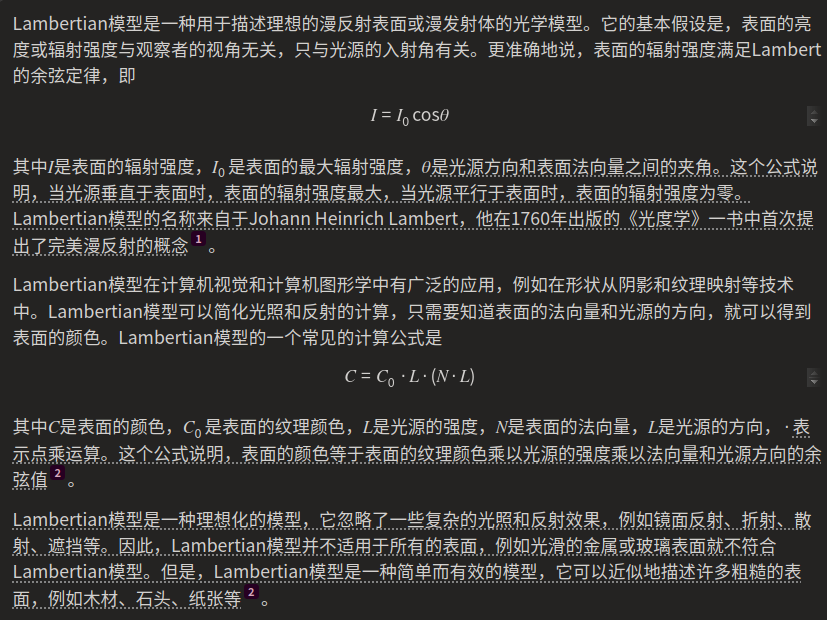
Lambertian模型(完美漫反射)
这里使用相乘的方式组合光照色和纹理色。根据这个模型,面朝光源的区域光照强度高,纹理色也相应增强。面背光源的区域光照弱,纹理色也被抑制。这样通过光照和纹理的结合,可以合成出具有照明效果的面部颜色,而不仅仅是固定的纹理本身的颜色。相乘方式可以近似实现不同光照方向下面…...

MATLAB的编程与应用,匿名函数、嵌套函数、蒙特卡洛法的掌握与使用
目录 1.匿名函数 1.1.匿名函数的定义与分类 1.2.匿名函数在积分和优化中应用 2.嵌套函数 2.1.嵌套函数的定义与分类 2.2.嵌套函数彼此调用关系 2.3.嵌套函数在积分和微分中应用 3.微分和积分 4.蒙特卡洛法 4.1.圆周率的模拟 4.2.计算N重积分(均匀分布&am…...
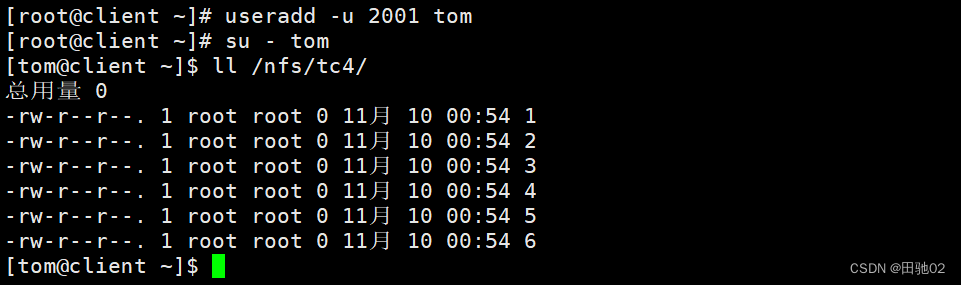
NFS服务器的搭建
架设一台NFS服务器,并按照以下要求配置 准备阶段:准备两台虚拟机,一台作为服务端,一台作为客户端 服务端(Server):192.168.75.139 客户端(Client):192.168.75.160 两…...

安卓Frida 常用脚本
打印调用堆栈, hook 某个方法,想看下调用堆栈,代码如下: function showStacks() {Java.perform(function () {send(Java.use("android.util.Log").getStackTraceString(Java.use("java.lang.Exception").$new()));});} 二,需要hook okhttp3 HttpUrl …...
机器学习数据预处理——Word2Vec的使用
引言: Word2Vec 是一种强大的词向量表示方法,通常通过训练神经网络来学习词汇中的词语嵌入。它可以捕捉词语之间的语义关系,对于许多自然语言处理任务,包括情感分析,都表现出色。 代码: 重点代码&#…...
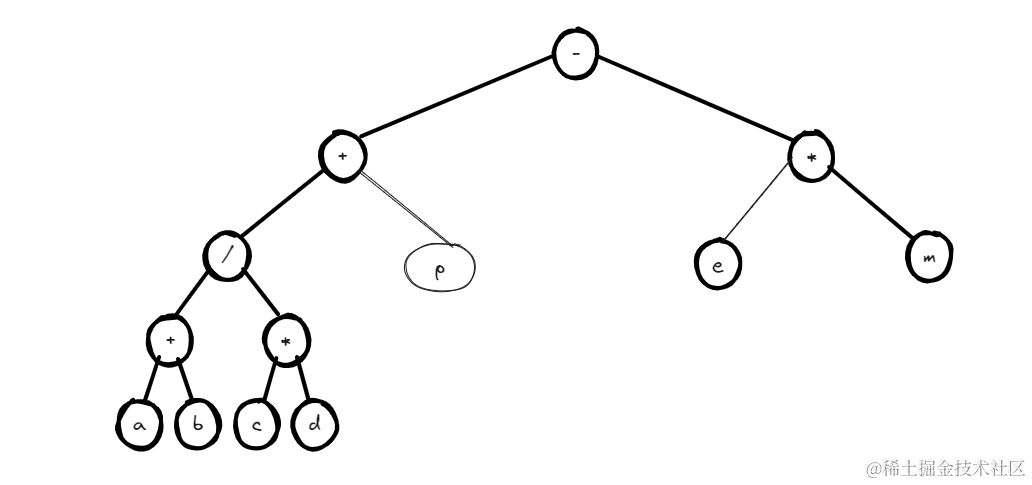
面试算法常考题之-------逆波兰式合集
逆波兰式背景介绍 逆波兰式是一种特殊的数学表达式表示法,它的诞生背景可以追溯到20世纪30年代。当时,波兰数学家Jan Wjtowicz和Wacław Sierpiński提出了一种新的数学表达式表示法,这种表示法将运算符放在操作数之后,而不是传统…...

独热编码和Word2Vec的区别
独热编码和Word2Vec都是自然语言处理中将词向量化的方式,但它们之间并没有直接的关系或依赖性。它们可以被视为在处理词向量时的两种不同方法或策略。 独热编码是一种简单直观的方法,每个词被表示为一个长向量,其中只有一个元素是1࿰…...

RestTemplate.postForEntity 方法进行 HTTP POST 请求
RestTemplate 是 Spring Framework 提供的一个用于处理 HTTP 请求的客户端工具。其中,postForEntity 是 RestTemplate 提供的用于发送 HTTP POST 请求并返回 ResponseEntity 对象的方法。 public <T> ResponseEntity<T> postForEntity(String url, Obj…...

盘点双11!阿里妈妈助这些品牌短视频赢增长!
刚刚!一年一度的双11落下帷幕,很多新变化值得回味。 尽管天气在变凉,但市场出现了逐渐回暖的迹象。在此背景下,大量商家特别关心如何在双11打一场漂亮的胜仗。 卖方如何行动,关键在于买方的变化。在阿里妈妈发布的《…...
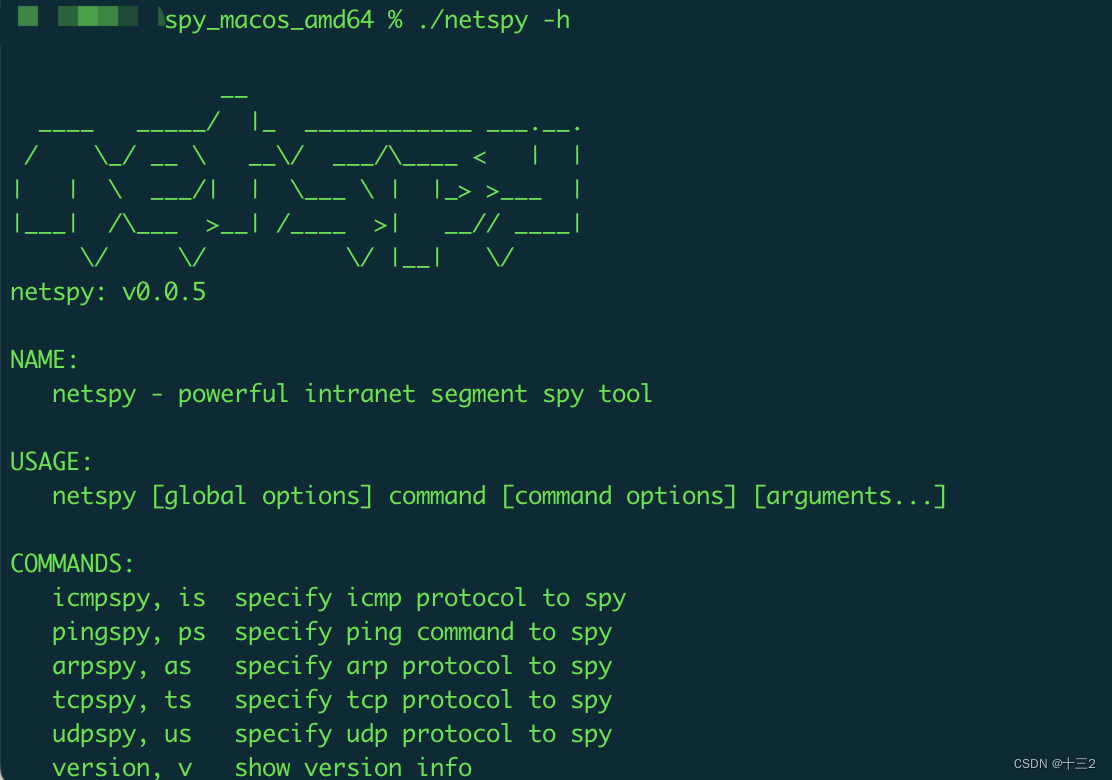
内网可达网段探测netspy- Mac环境
netspy是一款快速探测内网可达网段工具 当我们进入内网后想要扩大战果,那我们可能首先想知道当前主机能通哪些内网段。 netspy正是一款应用而生的小工具,体积较小,速度极快,支持跨平台,支持多种协议探测,…...

Liunx命令汇总
一.用户相关命令 1.1账号管理 创建用户: useradd (选项) 用户名用户口令: passwd (选项) 用户名修改用户: usermod 选项 用户名删除用户: userdel (选项) 用…...
自动控制原理--面试问答题
以下文中的,例如 s_1 为 s下角标1。面试加油! 控制系统的三要素:稳准快。稳,系统最后不能震荡、发散,一定要收敛于某一个值;快,能够迅速达到系统的预设值;准,最后稳态值…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

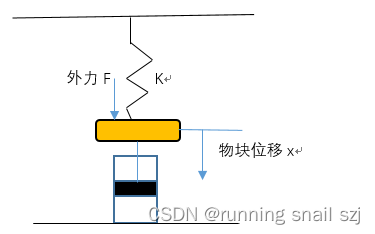
MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
