数据结构:树的基本概念(二叉树,定义性质,存储结构)
目录
- 1.树
- 1.基本概念
- 1.空树
- 2.非空树
- 2.基本术语
- 1.结点之间的关系描述
- 2.结点、树的属性描述
- 3.有序树、无序树
- 4.森林
- 3.树的常考性质
- 2.二叉树
- 1.基本概念
- 2.特殊二叉树
- 1.满二叉树
- 2.完全二叉树
- 3.二叉排序树
- 4.平衡二叉树
- 3.常考性质
- 4.二叉树的存储结构
- 1.顺序存储
- 2.链式存储
1.树
1.基本概念
树是n (n>=0)个结点的有限集合,n =0时,称为
空树,这是一种特殊情况。
在任意一棵非空树中应满足:
①有且仅有一个特定的称为根的结点。
②当n>1时,其余结点可分为m (m>0)个互不相交的有限集合T1,T2…… Tm,其中每个集合本身又是一棵树,并且称为根结点的子树。
③树是一种递归定义的数据结构。
1.空树
结点数为0的树。
2.非空树
①有且仅有一个根节点
②没有后继的结点称为“叶子结点”(或终端结点)
③有后继的结点称为“分支结点”(或非终端结点)
④除了根节点外,任何一个结点都有且仅有一个前驱
⑤每个结点可以有0个或多个后继。
2.基本术语
1.结点之间的关系描述
①祖先结点
②子孙结点
③双亲结点(父节点)
④孩子结点
⑤兄弟结点
⑥堂兄弟结点
⑦路径:只能从上而下
⑧路径长度:经过几条边
2.结点、树的属性描述
①结点的
层次(深度):从上往下数(默认从1开始)
②结点的高度:从下往上数
③树的高度(深度):总共多少层
④结点的度:有几个孩子(分支)
⑤树的度:各结点的度的最大值
3.有序树、无序树
①有序树――逻辑上看,树中结点的各子树从左至右是
有次序的,不能互换
②无序树――逻辑上看,树中结点的各子树从左至右是无次序的,可以互换
4.森林
森林是m ( m≥0)棵互不相交的树的集合。
3.树的常考性质
①
结点数=总度数+1
②度为m的树、m叉树的区别
树的度:各结点的度的最大值
m叉树:每个结点最多只能有m个孩子的树
③度为m的树第i层至多有 m i − 1 m^{i-1} mi−1个结点( i≥1)
④高度为h的m叉树至多有 m h − 1 m − 1 \frac{m^h-1}{m-1} m−1mh−1个结点。(等比数列求和)
⑤高度为h的m叉树至少有h个结点。
高度为h、度为m的树至少有h+m-1个结点。
⑥具有n个结点的m叉树的最小高度为 [ l o g m ( n ( m − 1 ) + 1 ) ] [log_m^{(n(m - 1)+ 1)}] [logm(n(m−1)+1)](向上取整)
2.二叉树
1.基本概念
二叉树是n (n≥0)个结点的有限集合:
①或者为空二叉树,即n = 0。
②或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。
左子树和右子树又分别是一棵二叉树。
特点:①每个结点至多只有两棵子树②左右子树不能颠倒(二叉树是有序树)
2.特殊二叉树
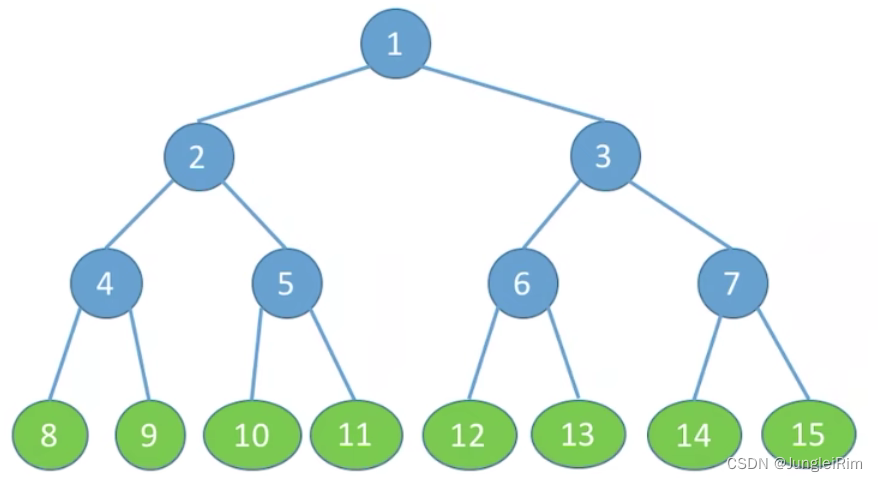
1.满二叉树
一棵高度为h,且含有 2 h − 1 2^h-1 2h−1个结点的二叉树
特点:
①只有最后一层有叶子结点
②不存在度为1的结点
③按层序从1开始编号,结点i的左孩子为2i,右孩子为2i+1;
结点i的父节点为[i/2] (向下取整)
2.完全二叉树
当且仅当其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应时,称为完全二叉树。
特点:
①只有最后两层可能有叶子结点
②最多只有一个度为1的结点
③按层序从1开始编号,结点i的左孩子为2i,右孩子为2i+1;
④i≤ [n/2]为分支结点,i>[n/2]为叶子结点(向下取整)
3.二叉排序树
一棵二叉树或者是空二叉树,或者是具有如下性质的二叉树:
左子树上所有结点的关键字均小于根结点的关键字;
右子树上所有结点的关键字均大于根结点的关键字。
左子树和右子树又各是一棵二叉排序树。(左小右大)
二叉排序树可用于元素的
排序、搜索。
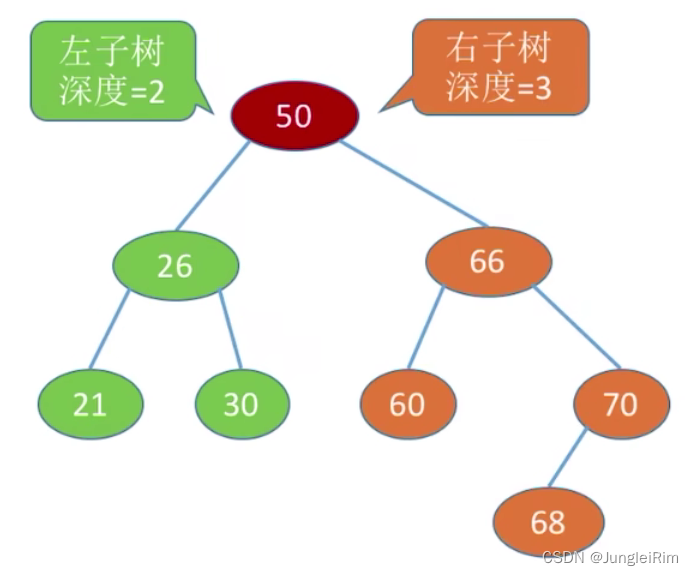
4.平衡二叉树
树上任一结点的左子树和右子树的
深度之差不超过1。
平衡二叉树能有更高的搜索效率。
3.常考性质
①:设非空二叉树中度为0、1和2的结点个数分别为n0,n1,和n2,则
n0= n2+ 1。(叶子结点比二分支结点多一个)
树的结点数=总度数+1
②二叉树第i层至多有 2 i − 1 2^{i-1} 2i−1个结点( i≥1)
③高度为h的二叉树至多有 2 h — 1 2^h —1 2h—1个结点(满二叉树)
④具有n个(n >0)结点的完全二叉树的高度h为 [ l o g 2 ( n + 1 ) ] ( 向上取整 ) 或 [ l o g 2 n ] + 1 (向下取整) [log_2^{(n + 1)}](向上取整)或[log_2^n]+ 1(向下取整) [log2(n+1)](向上取整)或[log2n]+1(向下取整)
⑤若完全二叉树有2k个(偶数)个结点,则必有n1=1,n0 = k, n2 = k-1;
若完全二叉树有2k-1个(奇数)个结点,则必有n1=0,n0 = k, n2 = k-1.
4.二叉树的存储结构
1.顺序存储
二叉树的顺序存储中,
一定要把二叉树的结点编号与完全二叉树对应起来。
利用完全二叉树,父节点与孩子结点的关系,存放在指定数组下标。
最坏情况:高度为h 且只有h个结点的单支树(所有结点只有右孩子),也至少需要 2 h − 1 2^h-1 2h−1个存储单元。
结论:二叉树的顺序存储结构,只适合存储完全二叉树。
2.链式存储
n个结点的
二叉链表共有n+1个空链域。
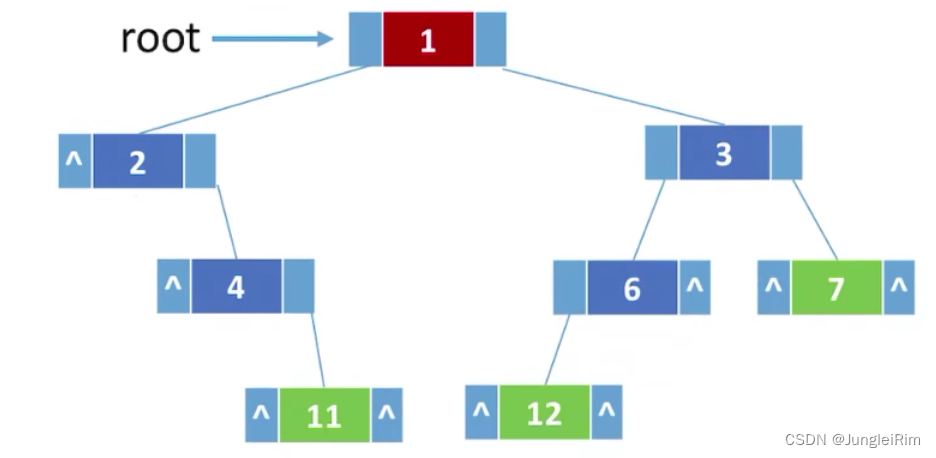
使用
三叉链表――方便找父结点。
相关文章:

数据结构:树的基本概念(二叉树,定义性质,存储结构)
目录 1.树1.基本概念1.空树2.非空树 2.基本术语1.结点之间的关系描述2.结点、树的属性描述3.有序树、无序树4.森林 3.树的常考性质 2.二叉树1.基本概念2.特殊二叉树1.满二叉树2.完全二叉树3.二叉排序树4.平衡二叉树 3.常考性质4.二叉树的存储结构1.顺序存储2.链式存储 1.树 1.…...

【Qt之QStandardItemModel类】介绍
描述 QStandardItemModel类提供了一个通用的模型,用于存储自定义数据。QStandardItemModel可以用作Qt标准数据类型的存储库。它是 Model/View类 之一,是 Qt的model/view框架 的一部分。 QStandardItemModel提 供了一种基于项目的传统方法来处理模型。 Q…...

01-Spring中的工厂模式
工厂模式 工厂模式的三种形态: 工厂模式是解决对象创建问题的属于创建型设计模式,Spring框架底层使用了大量的工厂模式 第一种:简单工厂模式是工厂方法模式的一种特殊实现,简单工厂模式又叫静态工厂方法模式不属于23种设计模式之一第二种:工厂方法模式…...

Linux是什么,Linux系统介绍
很多小伙伴都不是那么了解和知道Linux,到底Linux是什么? 像大家用到的安卓手机,生活中用到的各种智能设备,比如路由器,光猫,智能家具等,很多都是在Linux操作系统上。 Linux是什么?Li…...
:使用多线程对36手机高清壁纸批量抓取)
爬虫项目(11):使用多线程对36手机高清壁纸批量抓取
文章目录 书籍推荐目标网址单线程实现多线程实现爬取结果书籍推荐 如果你对Python网络爬虫感兴趣,强烈推荐你阅读《Python网络爬虫入门到实战》。这本书详细介绍了Python网络爬虫的基础知识和高级技巧,是每位爬虫开发者的必读之作。详细介绍见👉: 《Python网络爬虫入门到…...
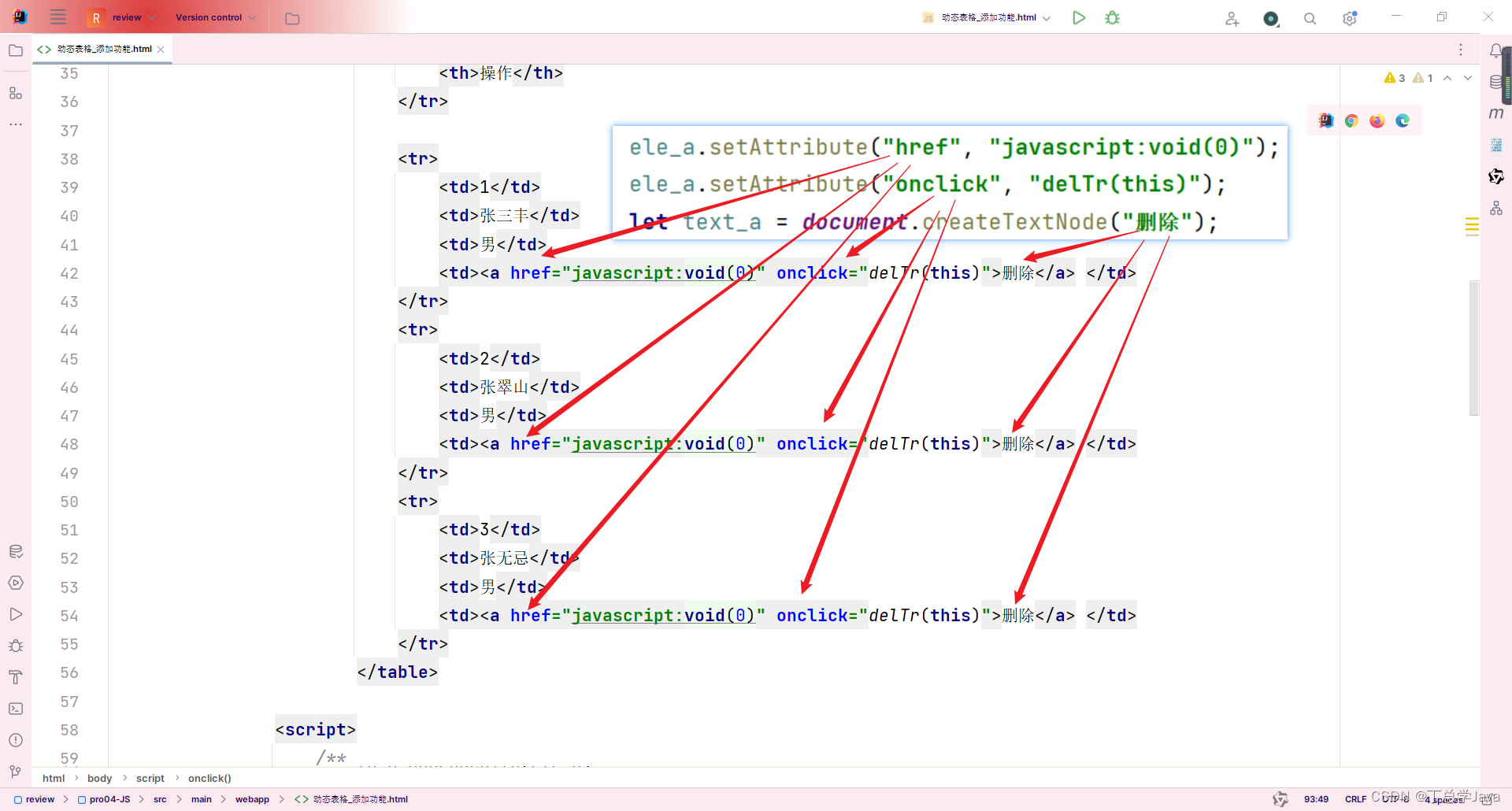
JavaScript_动态表格_删除功能
1、动态表格_删除功能 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>动态表格_添加和删除功能</title><style>table{border: 1px solid;margin: auto;width: 100%;}td,th{text-align: …...
)
一步一步开发微信小程序(Django+Mysql)
前提:假设你已经安装好Anaconda,微信开发者工具,MySQL数据库,IDE等工具 工具下载地址: Anaconda:https://www.anaconda.com/download MySQL:https://dev.mysql.com/downloads/mysql/ 微信开…...
mysql 讲解(1)
文章目录 前言一、基本的命令行操作二、操作数据库语句2.1、创建数据库2.2、删除数据库2.3、使用数据库2.4 查看所有数据库 三、列的数据类型3.1 字符串3.2 数值3.3 时间日期3.4 空3.5 int 和 varchar问题总结: 四、字段属性4.1 UnSigned4.2 ZEROFILL4.3 Auto_InCre…...
)
k8s关于metadata、spec.containers、spec.volumes的属性介绍(yaml格式)
目录 一.metadata常用属性 二.spec.containers子属性介绍 explain pod.spec.containers给出的参考 1.command示例演示 2.env和envFrom示例演示 3.ports部分详解 4.resources部分详解 5.startupProbe格式演示 6.terminationMessagePath和terminationMessagePolicy格式演…...
腾讯域名优惠卷领取
腾讯域名到到期了,听说申请此计划,可获得优惠卷,看到网上5年域名只需要10元,姑且试试看。 我的博客即将同步至腾讯云开发者社区,邀请大家一同入驻:https://cloud.tencent.com/developer/support-plan?in…...
elastic-job 完结篇
一 elastic-job 1.1 案例场景分析 1.设置4个分片,10秒执行一次。 分片弹性扩容缩容机制测试: 测试1:测试窗口1不关闭,再次运行main方法查看控制台日志,注意修改application.properties中的 server.port…...
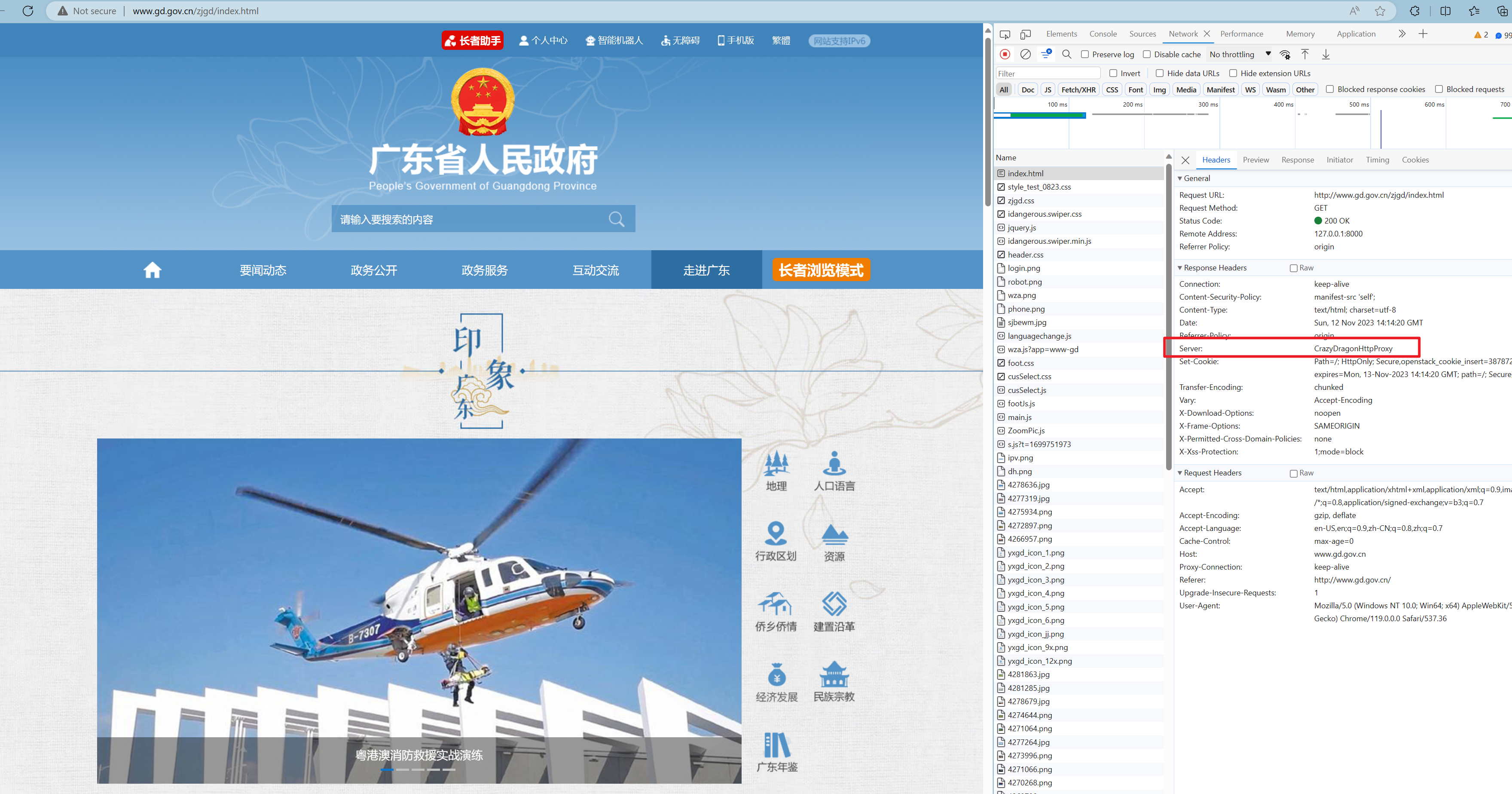
基于 Gin 的 HTTP 代理 demo
上次用 TCP 模拟了一个 HTTP 代理之后,感觉那样还是太简陋了,想着是不是可以用框架来做一个有点实际用处的东西。所以,就思索如何用 golang 的 Gin 框架来实现一个?嗯,对的你没有听错,是 gin 框架。你可能会…...
【ATTCK】MITRE Caldera - 测试数据泄露技巧
CALDERA是一个由python语言编写的红蓝对抗工具(攻击模拟工具)。它是MITRE公司发起的一个研究项目,该工具的攻击流程是建立在ATT&CK攻击行为模型和知识库之上的,能够较真实地APT攻击行为模式。 通过CALDERA工具,安全…...

【数据结构】树与二叉树(十二):二叉树的递归创建(算法CBT)
文章目录 5.2.1 二叉树二叉树性质引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。引理5.2:高度为k的二叉树中至多有 2 k 1 − 1 2^{k1}-1 2k1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。引理5.3&…...

Qt绘制网格和曲线
绘制网格: void Widget::drawGrid(QPainter &p, QRect &windRect) {QRect rect(windRect.left()m_margins.left(),windRect.top()m_margins.top(),windRect.width()-m_margins.left()-m_margins.right(),windRect.height()-m_margins.top()-m_margins.bo…...

2023-11-12
今日比较摆烂, 但是把自写管道的原理搞懂了, 主要是把 exp 完完全全看懂了, 还不错. 然后就没干啥了. 明日计划: 学校的作业. AFL 源码. 我真是服了我自己了, AFL 源码搁多久了, 操操操 然后把 seccomp 重新学习下...

[工业自动化-16]:西门子S7-15xxx编程 - 软件编程 - 西门子仿真软件PLCSIM
目录 前言: 一、PLCSIM仿真软件 1.1 PLCSIM仿真软件基础版(内嵌) 1.2 PLCSIM仿真软件与PLCSIM仿真软件高级版的区别? 1.3 PLCSIM使用 前言: PLC集成开发环境是运行在Host主机上,Host主机与PLC可以通过…...

运行npm install卡住不动的几种解决方案
在前端开发经常会遇到运行npm install 来安装工具包一直卡住不动,为此这里提供几种解决方案,供大家参考学习,不足之处还请指正。 第一种方案、首先检查npm代理,是否已经使用国内镜像 // 执行以下命令查看是否为国内镜像 npm con…...
[Android]_[初级]_[配置gradle的环境变量设置安装位置]
场景 在开发Android项目的时候, gradle是官方指定的构建工具。不同项目通过wrapper指定不同版本的gradle。随着项目越来越多,使用的gradle版本也增多,导致它以来的各种库也增加,系统盘空间不足,怎么解决? 说明 grad…...
docker更改存储目录原因及方案
为什么一定要将docker的存储目录挂载到其他目录 docker在安装时默认存储目录在/var/lib/docker,而该目录是在系统盘下的。docker安装后,会使用各种各样的镜像,动辄几个G,那么如此多的镜像文件,装着装着系统盘就撑爆了…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...