【论文阅读】FreeMatch: Self-adaptive Thresholding for Semi-supervised Learning
论文下载
GitHub
bib:
@INPROCEEDINGS{wang2023freematch,title = {FreeMatch: Self-adaptive Thresholding for Semi-supervised Learning},author = {Wang, Yidong and Chen, Hao and Heng, Qiang and Hou, Wenxin and Fan, Yue and and Wu, Zhen and Wang, Jindong and Savvides, Marios and Shinozaki, Takahiro and Raj, Bhiksha and Schiele, Bernt and Xie, Xing},booktitle = {ICLR},year = {2023},pages = {1--20}
}
1. 摘要
-
Semi-supervised Learning (SSL) has witnessed great success owing to the impressive performances brought by various methods based on pseudo labeling and consistency regularization.
半监督学习(semi-supervised learning)的两大杀器,pseudo labeling(伪标记)和consistency regularization(一致性正则)。
-
However, we argue that existing methods might fail to utilize the unlabeled data more effectively since they either use a pre-defined / fixed threshold or an ad-hoc threshold adjusting scheme, resulting in inferior performance and slow convergence.
提出现有方法的不足,use a pre-defined / fixed threshold or an ad-hoc threshold adjusting scheme。这里的阈值应该是伪标签加入的阈值,只有大于阈值的伪标签才会加入训练,这一点在基于伪标签技术的方法中十分的常用。至于基于一致性正则中是否也存在这样的阈值,这一点是存疑的。
-
We first analyze a motivating example to obtain intuitions on the relationship between the desirable threshold and model’s learning status. Based on the analysis, we hence propose FreeMatch to adjust the confidence threshold in a self-adaptive manner according to the model’s learning status.
顺利提出自己的核心创新点: self-adaptive confidence threshold。
-
We further introduce a self-adaptive class fairness regularization penalty to encourage the model for diverse predictions during the early training stage.
一个trick,避免模型初期过早收敛。
-
Extensive experiments indicate the superiority of FreeMatch especially when the labeled data are extremely rare. FreeMatch achieves 5.78%, 13.59%, and 1.28% error rate reduction over the latest state-of-the-art method FlexMatch on CIFAR-10 with 1 label per class, STL-10 with 4 labels per class, and ImageNet with 100 labels per class, respectively. Moreover, FreeMatch can also boost the performance of imbalanced SSL.
自信的算法用三句话来描述自己是art-of-state的。
-
The codes can be found at https: //github.com/microsoft/Semi-supervised-learning.
代码地址。
2. 算法描述
2.1. 例子
通过一个分类的例子,有以下有趣的结论:
- 简单地说,未标记数据利用率(采样率) 1 − P ( Y p = 0 ) 1−P(Y_p = 0) 1−P(Yp=0) 直接由阈值 τ \tau τ 控制。随着置信度阈值 τ \tau τ 变大,未标记数据利用率变低。在训练初期,由于 β \beta β 仍然很小,采用较高的阈值可能会导致采样率较低且收敛速度较慢。
- 更有趣的是,如果 σ 1 ≠ σ 2 \sigma_1 \neq \sigma_2 σ1=σ2,则 P ( Y p = 1 ) ≠ P ( Y p = − 1 ) P(Y_p = 1) \neq P(Y_p = −1) P(Yp=1)=P(Yp=−1)。事实上, τ \tau τ 越大,伪标签越不平衡。从我们旨在解决平衡分类问题的意义上来说,这可能是不可取的。不平衡的伪标签可能会扭曲决策边界并导致所谓的伪标签偏差。对此的一个简单的补救措施是使用特定于类的阈值 τ 2 \tau_2 τ2 和 1 − τ 1 1 − \tau_1 1−τ1 来分配伪标签。(
different classes have different levels of intra-class diversity (different σ)) - 采样率 1 − P ( Y p = 0 ) 1 − P(Y_p = 0) 1−P(Yp=0) 随着 μ 2 − μ 1 \mu_2 − \mu_1 μ2−μ1 变小而降低。换句话说,两个类越相似,未标记的样本就越有可能被屏蔽。随着两个类别变得更加相似,特征空间中会混合更多的样本,而模型对其预测的信心较差,因此需要一个适度的阈值来平衡采样率。否则,我们可能没有足够的样本来训练模型来对已经很难分类的类进行分类。(
some classes are harder to classify than others (µ2 − µ1 being small)
Since different classes have different levels of intra-class diversity (different σ) and some classes are harder to classify than others (µ2 − µ1 being small), a fine-grained
class-specific thresholdis desirable to encourage fair assignment of pseudo labels to different classes.
2.2. Self-adaptive Threshold
Global Threshold:
τ t = { 1 C , if t = 0 , λ τ t − 1 + ( 1 − λ ) 1 μ B ∑ b = 1 μ B max q b , otherwise . \tau_t= \begin{cases} \frac{1}{C},& \text{if } t=0,\\ \lambda\tau_{t-1} + (1-\lambda)\frac{1}{\mu B}\sum_{b=1}^{\mu B}\max{q_b},& \text{otherwise}. \end{cases} τt={C1,λτt−1+(1−λ)μB1∑b=1μBmaxqb,if t=0,otherwise.
Local Threshold:
p ~ t ( c ) = { 1 C , if t = 0 , λ p ~ t − 1 ( c ) + ( 1 − λ ) 1 μ B ∑ b = 1 μ B q b ( c ) , otherwise . \widetilde{p}_t(c)= \begin{cases} \frac{1}{C},& \text{if } t=0,\\ \lambda\widetilde{p}_{t-1}(c) + (1-\lambda)\frac{1}{\mu B}\sum_{b=1}^{\mu B}q_b(c),& \text{otherwise}. \end{cases} p t(c)={C1,λp t−1(c)+(1−λ)μB1∑b=1μBqb(c),if t=0,otherwise.
Final Threshold:
τ t ( c ) = MaxNorm ( p ~ t ( c ) ) ⋅ τ t \tau_t(c) = \text{MaxNorm}(\widetilde{p}_t(c)) \cdot \tau_t τt(c)=MaxNorm(p t(c))⋅τt
一致性正则:
L u = 1 μ B ∑ b = 1 μ B I ( max ( q b ) ≥ τ t ( arg max ( q b ) ) ) ⋅ H ( q ^ b , Q b ) \mathcal{L}_u = \frac{1}{\mu B}\sum_{b=1}^{\mu B}\mathbb{I}(\max(q_b) \geq \tau_t(\argmax(q_b)))\cdot \mathcal{H}(\hat{q}_b, Q_b) Lu=μB1b=1∑μBI(max(qb)≥τt(argmax(qb)))⋅H(q^b,Qb)
Notice: 原文中,指示函数少打了个括号
2.3. Self-adaptive Fairness
KL散度:
D K L ( p ∥ q ) = ∑ i = 1 n p ( x i ) log ( p ( x i ) q ( x i ) ) D_{KL}(p\|q) = \sum_{i=1}^np(x_i)\log(\frac{p(x_i)}{q(x_i)}) DKL(p∥q)=i=1∑np(xi)log(q(xi)p(xi))
其中:
- p表示样本的真实分布,q表示模型的预测分布。从KL散度公式中可以看到q分布越接近p(q分布越拟合p),那么散度值越小,即损失值越小。
- KL散度称为KL距离,但它并不满足距离的性质:1. KL散度不是对称的;2. KL散度不满足三角不等式。
交叉熵:
D K L ( p ∥ q ) = ∑ i = 1 n p ( x i ) log ( p ( x i ) q ( x i ) ) = ∑ i = 1 n p ( x i ) log ( p ( x i ) ) − ∑ i = 1 n p ( x i ) log ( q ( x i ) ) = − H ( p ( x ) ) + [ − ∑ i = 1 n p ( x i ) log ( q ( x i ) ) ] \begin{align*} D_{KL}(p\|q) &= \sum_{i=1}^np(x_i)\log(\frac{p(x_i)}{q(x_i)})\\ &= \sum_{i=1}^n p(x_i)\log(p(x_i)) - \sum_{i=1}^n p(x_i)\log(q(x_i)) \\ &= -\mathcal{H}(p(x)) + [-\sum_{i=1}^n p(x_i)\log(q(x_i))] \end{align*} DKL(p∥q)=i=1∑np(xi)log(q(xi)p(xi))=i=1∑np(xi)log(p(xi))−i=1∑np(xi)log(q(xi))=−H(p(x))+[−i=1∑np(xi)log(q(xi))]
其中:
- 等式的前一部分恰巧就是p的熵(表示信息量),等式的后一部分,就是交叉熵。
- 在机器学习中,我们需要评估label(GroundTruth)和predicts之间的差距,使用KL散度刚刚好,即:由于KL散度中的前一部分 − H ( y ) −\mathcal{H}(y) −H(y)不变,故在优化过程中,只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss,评估模型。而在拟合可变分布时,则采用
KL散度。
本文提出的SAF正则是基于《Joint Optimization Framework for Learning with Noisy Labels》中的工作的。《Pseudo-Labeling and Confirmation Bias in Deep Semi-Supervised Learning》中的工作则是基于此的,并没有做更改。
The regularization loss L p ( θ ∣ X ) L_p(\theta|X) Lp(θ∣X) is required to prevent the assignment of all labels to a single class: In the case of minimizing only Eq. (6), we obtain a trivial global optimal solution with a network that always predicts constant one-hot y ^ ∈ H \hat{y} \in H y^∈H and each label y i = y ^ y_i = \hat{y} yi=y^ for any image x i x_i xi. To overcome this problem, we introduce a prior probability distribution p \mathbf{p} p, which is a distribution of classes among all training data. If the prior distribution of classes is known, then the updated labels should follow the same. Therefore, we introduce the KL-divergence from s ‾ ( θ , X ) \overline{s}(\theta,X) s(θ,X) to p \mathbf{p} p as a cost function as follows:
L p = ∑ j = 1 c p j log ( p j s ‾ ( θ , X ) ) \mathcal{L}_p = \sum_{j=1}^{c}p_j \log(\frac{p_j}{\overline{s}(\theta,X)}) Lp=j=1∑cpjlog(s(θ,X)pj)
s ‾ ( θ , X ) = ∑ i = 1 n s ( θ , x i ) \overline{s}(\theta,X) = \sum_{i=1}^{n}s(\theta,x_i) s(θ,X)=i=1∑ns(θ,xi)
Notice: 这里的正则是KL散度, p表示先验概率,这里采用的是均匀分布; s ‾ ( θ , X ) \overline{s}(\theta,X) s(θ,X) 表示模型的平均预测。
SAF:
这个正则的目的是鼓励模型对每个类别做出不同的预测,从而产生有意义的自适应阈值,特别是在标记数据很少的情况下。不同于只是要求模型对于无标记样本预测类别平衡(各个类别预测数量一样),数量波动也是自适应的。SAF 鼓励每个小批量的输出概率在通过直方图分布归一化后接近模型的边缘类分布。
p ‾ = 1 μ B ∑ b = 1 μ B I ( max ( q b ) ≥ τ t ( arg max ( q b ) ) ) Q b \overline{p} = \frac{1}{\mu B}\sum_{b=1}^{\mu B}\mathbb{I}(\max(q_b) \geq \tau_t(\argmax(q_b)))Q_b p=μB1b=1∑μBI(max(qb)≥τt(argmax(qb)))Qb
h ‾ = 1 μ B Hist μ B ( I ( max ( q b ) ≥ τ t ( arg max ( q b ) ) ) Q ^ b ) \overline{h} = \frac{1}{\mu B}\text{Hist}_{\mu B}(\mathbb{I}(\max(q_b) \geq \tau_t(\argmax(q_b)))\hat{Q}_b) h=μB1HistμB(I(max(qb)≥τt(argmax(qb)))Q^b)
h ~ t = λ h ~ t − 1 + ( 1 − λ ) Hist μ B ( q ^ b ) ) \widetilde{h}_t = \lambda \widetilde{h}_{t-1} + (1-\lambda)\text{Hist}_{\mu B}(\hat{q}_b)) h t=λh t−1+(1−λ)HistμB(q^b))
L f = − H ( SumNorm ( q ~ t h ~ t ) , SumNorm ( q ‾ t h ‾ t ) ) \mathcal{L}_f = -\mathcal{H}(\text{SumNorm}(\frac{\widetilde{q}_t }{\widetilde{h}_t }), \text{SumNorm}(\frac{\overline{q}_t }{\overline{h}_t })) Lf=−H(SumNorm(h tq t),SumNorm(htqt))
疑问?
- 这里的 L f \mathcal{L}_f Lf 表示交叉熵的相反数,那不是相当于是负数了。
- 这里魔改太多了,想了很久,还是没法明白这是为什么?
Answer:
我在这里尝试回答一下自己的疑问。
首先,可以肯定的是 L f \mathcal{L}_f Lf是负的。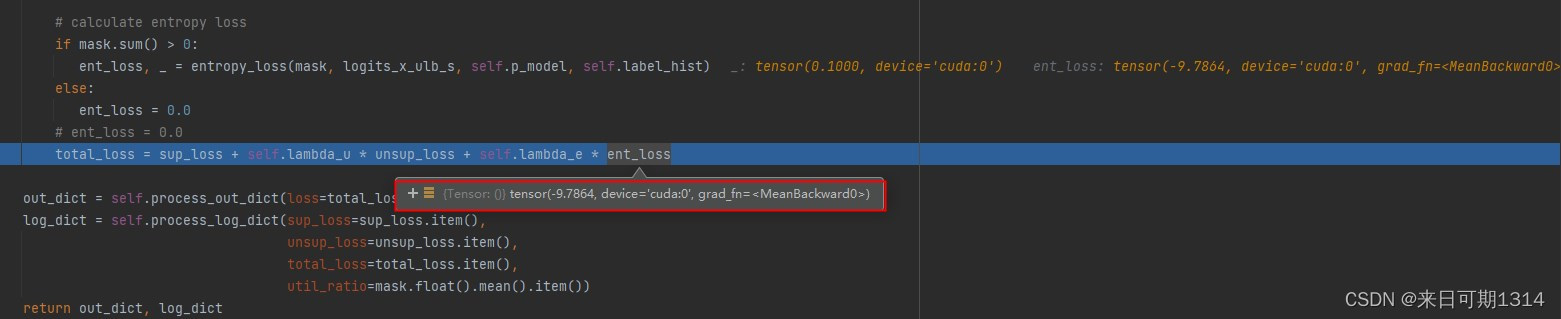
这里借鉴的 L f \mathcal{L}_f Lf可以理解为 SumNorm ( q ‾ t h ‾ t ) \text{SumNorm}(\frac{\overline{q}_t }{\overline{h}_t }) SumNorm(htqt)的熵,可以理解为信息量。但是信息量不能为负数,这里相当于最大化熵,即要求分布尽可能均匀,每个类的概率值相同。
那么现在就还有一个疑问了,为什么不是类似于 − H ( SumNorm ( q ‾ t h ‾ t ) , SumNorm ( q ‾ t h ‾ t ) ) -\mathcal{H}(\text{SumNorm}(\frac{\overline{q}_t }{\overline{h}_t }), \text{SumNorm}(\frac{\overline{q}_t }{\overline{h}_t })) −H(SumNorm(htqt),SumNorm(htqt))这样的形势。猜测是为了简化运算, SumNorm ( q ~ t h ~ t ) \text{SumNorm}(\frac{\widetilde{q}_t }{\widetilde{h}_t }) SumNorm(h tq t)其实是没有梯度值的,相当于是一个标量。当然这是强行解释了,其实不必纠结为什么吧,效果好就是了,原论文也没有进一步的解释。
3. 总结
论文写作技巧拉满了。关于自适应阈值这一块我倒是理解了,但是关于SAF这个负号我实在是没法理解。
相关文章:

【论文阅读】FreeMatch: Self-adaptive Thresholding for Semi-supervised Learning
论文下载 GitHub bib: INPROCEEDINGS{wang2023freematch,title {FreeMatch: Self-adaptive Thresholding for Semi-supervised Learning},author {Wang, Yidong and Chen, Hao and Heng, Qiang and Hou, Wenxin and Fan, Yue and and Wu, Zhen and Wang, Jindong and Savv…...

工业网关贴牌厂家有哪些?工业网关OEM厂家怎么选?
随着物联网技术的不断发展,市面上不断涌现出各种工业物联网厂商。中小型物联网企业苦于有技术,但是生产能力受限,需要寻找OEM代工厂家。但是在如何选择OEM代工厂家时又犯了难。工业网关类产品属于技术密集型产品,对厂家的生产能力…...
NetSuite 固定资产报表自定义原理及应用
NetSuite固定资产模块一直处于功能迭代更新中,目前23.2的版本能够支持报表的局部自定义,比如增加原值或已折旧期间,甚至固定资产自定义字段等。但是当我们在实际项目中,会遇到一些挑战,例如: 固定资产原值…...

【复杂网络建模】——基于关联矩阵构建超图网络
目录 一、复杂网络介绍 二、常规的构建方法 三、基于关联矩阵构建超图 一、复杂网络介绍 复杂网络是指由大量相互连接的元素或节点构成的网络,这些节点之间的连接关系通常是非常复杂和多样化的。这种网络结构通常用图论来表示,其中节点表示网络中的个体或元素,边表示它们…...

学习c#的第八天
目录 C# 方法 C# 中定义方法 C# 中调用方法 递归方法调用 参数传递 值参数 引用参数 输出参数 常见题 ref 和 out 的区别 方法中参数的类型有几种 扩展方法 对于复杂引用类型参数传递的控制 C# 方法 C# 中定义方法 在C#中定义方法时,需要遵循以下结构…...

我心目中的分布式操作系统
这是一位网友发给我的文字,我原样复制粘贴发出来给大家,他的观点我不过多评论,也不代表公司和研发团队的立场,但是最后一段本人不同意,因为Laxcus分布式操作系统已经发布了六个版本,在很多领域广泛部署使用…...
新型的铁塔基站“能源管家”
安科瑞 崔丽洁 引言:随着5G基站的迅猛发展,基站的能耗问题也越来越突出,高效可靠的基站配电系统方案,是提高基站能耗使用效率,实现基站节能降耗的重要保证,通过多回路仪表监测每个配电回路的用电负载情况&a…...

数字孪生智慧园区:大数据驱动下的运营管理革新
随着物联网、大数据、云计算等技术的飞速发展,数字孪生技术应运而生,它将物理世界与数字世界紧密连接起来,为各行各业提供了前所未有的解决方案。智慧园区作为城市的重要组成部分,通过数字孪生技术,可以实现更加高效、…...
sqli-labs关卡12(基于post提交的双引号闭合的字符型注入)通关思路
文章目录 前言一、回顾第十一关知识点二、靶场第十二关通关思路1、判断注入点2、爆显位个数3、爆显位位置4、爆数据库名5、爆数据库表名6、爆数据库列名7、爆数据库数据 总结 前言 此文章只用于学习和反思巩固sql注入知识,禁止用于做非法攻击。注意靶场是可以练习的…...
开放领域问答机器人2——开发流程和方案
开放领域问答机器人是指在任何领域都能够回答用户提问的智能机器人。与特定领域问答机器人不同,开放领域问答机器人需要具备更广泛的知识和更灵活的语义理解能力,以便能够回答各种不同类型的问题。 开发开放领域问答机器人的流程和方案可以包括以下步骤…...
)
pandas 常用45个操作方法(详解)
1、query函数进行数据筛选 相当于 bool 索引 data.query("Graduate_year==2020 & Language==Java")df.query("Language in [CPP,C,C#]") pandas.DataFrame.query(self, expr, inplace = False, **kwargs)Expr 评估查询字符inplace=False 修改数…...

PHP判断扫码支付扫码条码支付宝微信区分
微信:用户付款码规则:18位纯数字,前缀以10、11、12、13、14、15开头 支付宝:25~30开头的长度为16~24位的数字,实际字符串长度以开发者获取的付款码长度为准 <?php /*** 判断扫码支付的方式* param string $code 扫…...
一文了解芯片测试项目和检测方法 -纳米软件
芯片检测是芯片设计、生产、制造成过程中的关键环节,检测芯片的质量、性能、功能等,以满足设计要求和市场需求,确保芯片可以长期稳定运行。芯片测试内容众多,检测方法多样,今天纳米软件将为您介绍芯片的检测项目都有哪…...
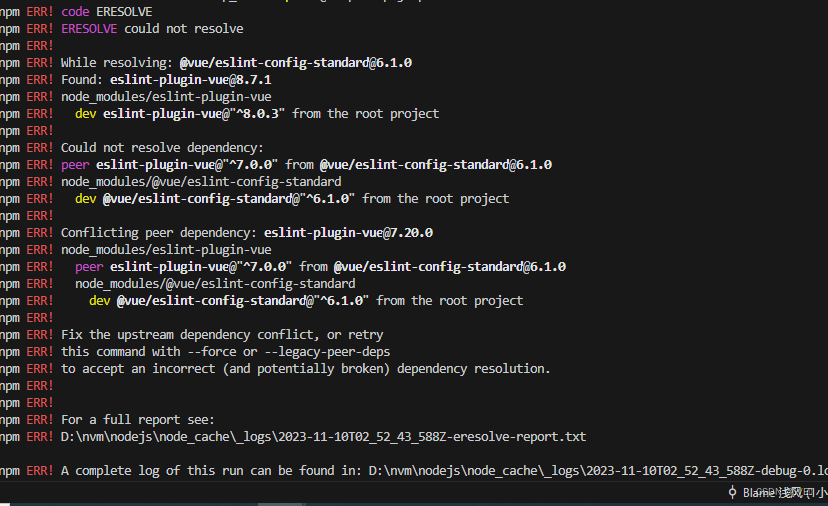
【npm 错误】:npm ERR! code ERESOLVE、npm ERR! ERESOLVE could not resolve问题
用过npm的小伙伴都会有这么一个情况出现,就是npm install /npm install xxxx 会出现改一连串的错误,如下: 解决办法: 只要在npm install后面加上--legacy-peer-deps就可以解决问题,安装插件也一样 npm install --legacy-peer-dep…...
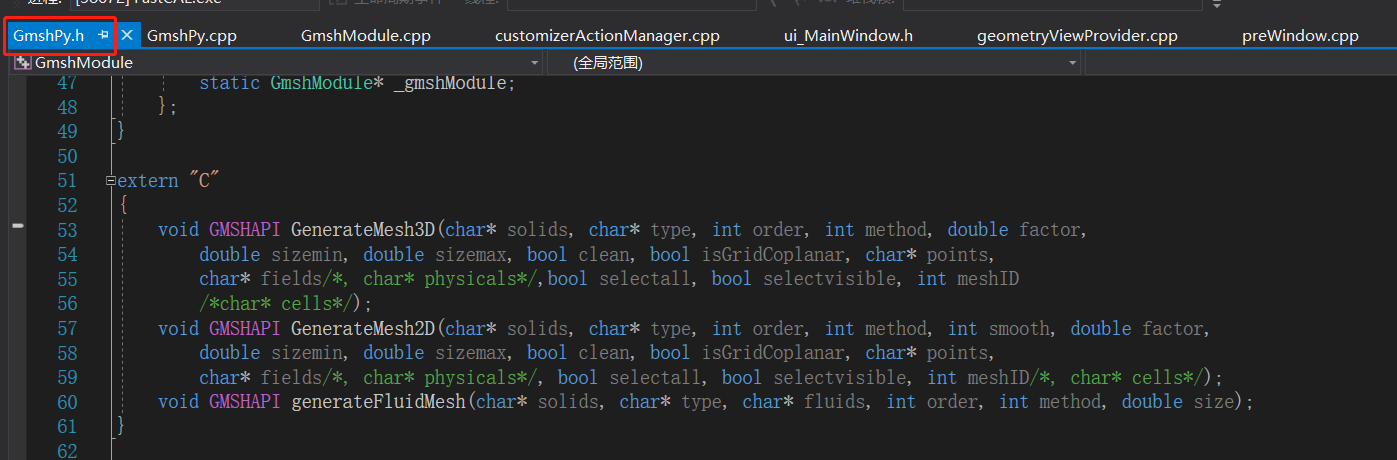
【FastCAE源码阅读8】调用gmsh生成网格
FastCAE使用gmsh进行网格划分,划分的时候直接启动一个新的gmsh进程,个人猜测这么设计是为了规避gmsh的GPL协议风险。 进行网格划分时,其大体运行如下图: 一、Python到gmshModule模块 GUI操作到Python这步不再分析,比…...
使用LLM-Tuning实现百川和清华ChatGLM的Lora微调
LLM-Tuning项目源码: GitHub - beyondguo/LLM-Tuning: Tuning LLMs with no tears💦, sharing LLM-tools with love❤️.Tuning LLMs with no tears💦, sharing LLM-tools with love❤️. - GitHub - beyondguo/LLM-Tuning: Tuning LLMs wit…...
浏览器标签页之间的通信
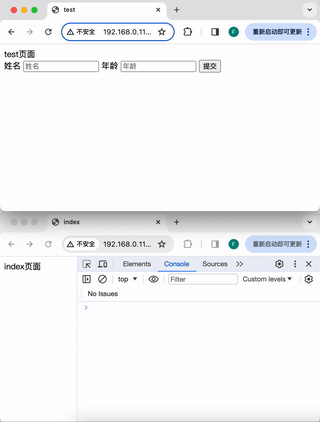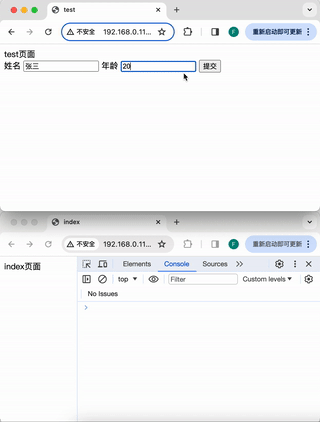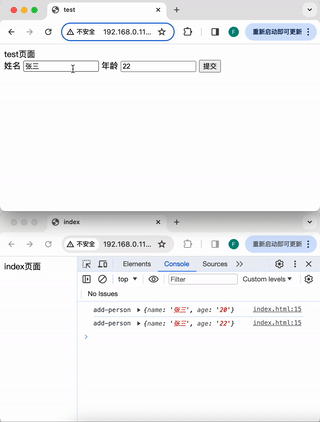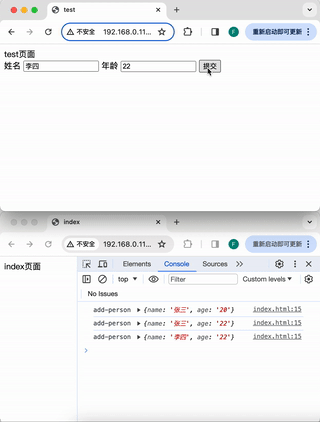
前言 在开发管理后台页面的时候,会遇到这样一种需求:有一个列表页面,一个新增按钮,一个新增页面,点击新增按钮,在一个新的标签页中打开新增页面。并且,新增后要自动实时的更新列表页面的数据。…...
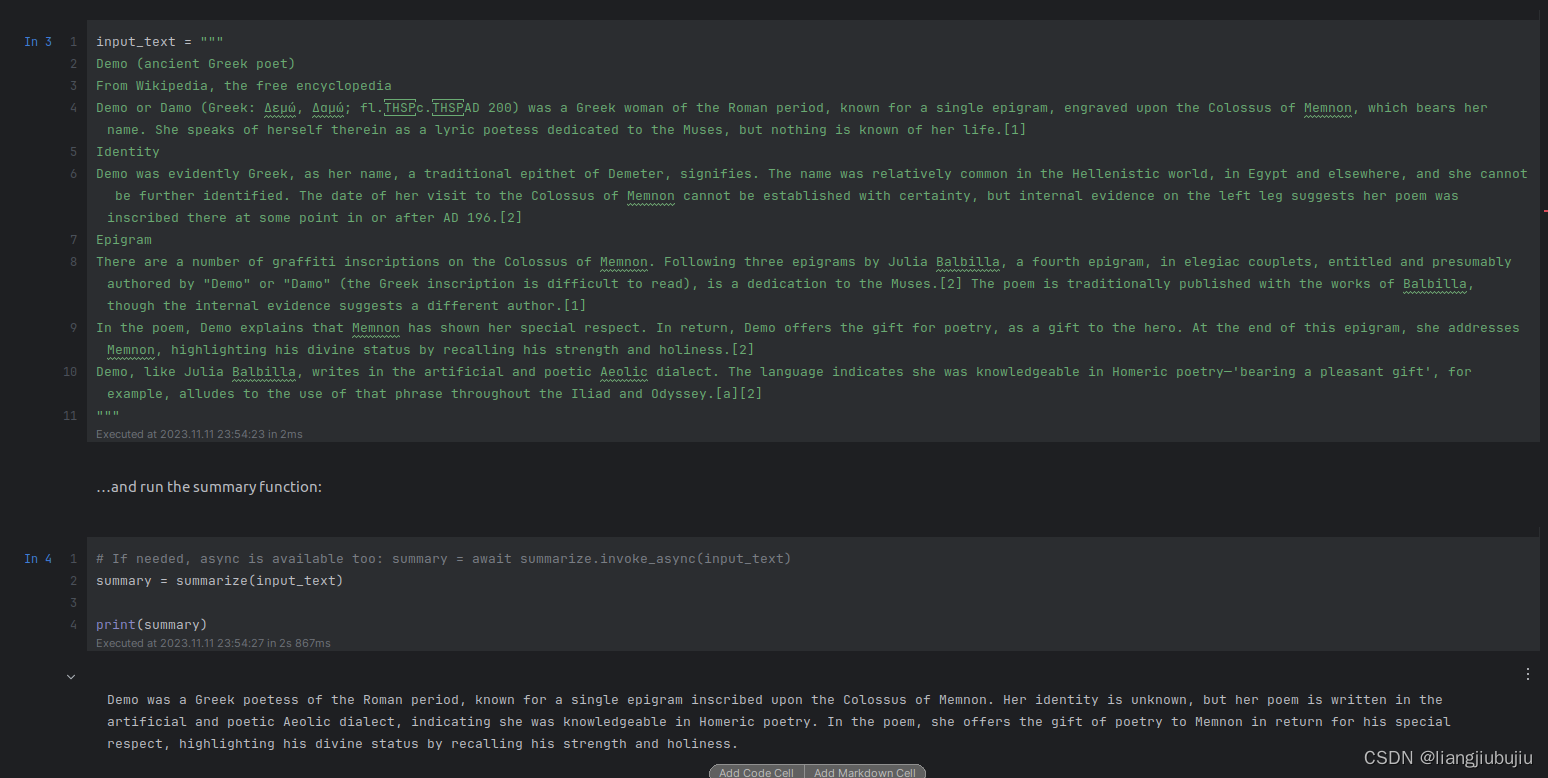
Semantic Kernel 学习笔记1
1. 挂代理跑通openai API 2. 无需魔法跑通Azure API 下载Semantic Kernel的github代码包到本地,主要用于方便学习python->notebooks文件夹中的内容。 1. Openai API:根据上述文件夹中的.env.example示例创建.env文件,需要填写下方两个内…...

图像二值化阈值调整——Triangle算法,Maxentropy方法
一. Triangle方法 算法描述:三角法求分割阈值最早见于Zack的论文《Automatic measurement of sister chromatid exchange frequency》主要是用于染色体的研究,该方法是使用直方图数据,基于纯几何方法来寻找最佳阈值,它的成立条件…...

监控视频片段合并完整视频|FFmpeg将多个视频片段拼接完整视频|PHP自动批量拼接合并视频
关于环境配置ffmpeg安装使用的看之前文章 哔哩哔哩缓存转码|FFmpeg将m4s文件转为mp4|PHP自动批量转码B站视频 <?php date_default_timezone_set("PRC"); header("Content-type: text/html; charsetutf-8"); set_time_limit(0);// 遍历获取文件 functi…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
