4.2 onnx简化模型结构
前言
对已有的onnx结构,进行简化操作,onnx提供两种常规操作
方式一
假设为 model.onnx, 比较简单粗暴
# 简化
onnxsim model.onnx model_sim.onnx
方式二
稍微复杂点,代码有点多
import onnx
import argparse
from onnxsim import simplify# Simplify
def simplify_model(args):onnx_model = onnx.load(args.origin_model)model_simp, check = simplify(onnx_model)model_simp = onnx.shape_inference.infer_shapes(model_simp)onnx.save(model_simp, args.output_model)print(" Simplify onnx Done.")# 检查onnx计算图
def checknet(model_path):model = onnx.load(model_path)onnx.checker.check_model(model) # Print a human readable representation of the graph# print(onnx.helper.printable_graph(model.graph))def parse_args():parser = argparse.ArgumentParser()parser.add_argument("--origin_model", type=str)parser.add_argument("--output_model", type=str)args = parser.parse_args()return argsif __name__ == "__main__":args = parse_args()simplify_model(args
总结
- 两种本质上没用改变,都是通过调用onnxsim进行操作
- 看个人使用时机
相关文章:

4.2 onnx简化模型结构
前言 对已有的onnx结构,进行简化操作,onnx提供两种常规操作 方式一 假设为 model.onnx, 比较简单粗暴 # 简化 onnxsim model.onnx model_sim.onnx方式二 稍微复杂点,代码有点多 import onnx import argparse from onnxsim import simpl…...

通用的链栈实现(C++)
template<class T> class MyStack//链栈 { private:struct StackNode{T data;StackNode* next;StackNode(const T& val T(), StackNode* p nullptr) :data(val), next(p) {}//};StackNode* top;int cursize;void clone(const MyStack& s){Clear();cursize s.c…...

物联网AI MicroPython学习之语法 bluetooth蓝牙
学物联网,来万物简单IoT物联网!! bluetooth 介绍 该模块为板上的蓝牙控制器提供了相关接口。目前支持低功耗蓝牙 (BLE)的Central(中央), Peripheral(外设), Broadcaster(广播者&…...
React中的key有什么作用?
一、是什么 首先,先给出react组件中进行列表渲染的一个示例: const data = [ { id: 0, name: abc }, { id: 1, name: def }, { id: 2, name: ghi }, { id: 3, name: jkl } ]; const ListItem = (props) => { return <li>{props.name}</li>; }; con…...

初认识vue,v-for,v-if,v-bind,v-model,v-html等指令
vue 一.vue3介绍 1.为什么data是函数而不是对象? 因为vue是组件开发,组件会多次复用,data如果是对象,多次复用是共享,必须函数返回一个新的对象 1. 官网初识 Vue (发音为 /vjuː/,类似 view) 是一款用于构建用户界面的 JavaScript 框架。它基于标准 HTML、CSS …...
Java 算法篇-深入了解单链表的反转(实现:用 5 种方式来具体实现)
🔥博客主页: 小扳_-CSDN博客 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 单链表的反转说明 2.0 单链表的创建 3.0 实现单链表反转的五种方法 3.1 实现单链表反转 - 循环复制(迭代法) 3.2 实现单链表反转 - 头插法 3…...

Android 10.0 系统内存优化之修改dalvik虚拟机的内存参数
1.前言 在10.0的系统开发定制中,app应用也是运行在dalvik虚拟机上的,所以对于一些内存低的系统中,在某些大应用会出现耗内存 卡顿情况,这是系统分配的内存不够大,在进行耗内存的操作,就会出现频繁gc等等原因造成不流畅的现象,接下来就分析下 虚拟机分配内存的相关原理 …...
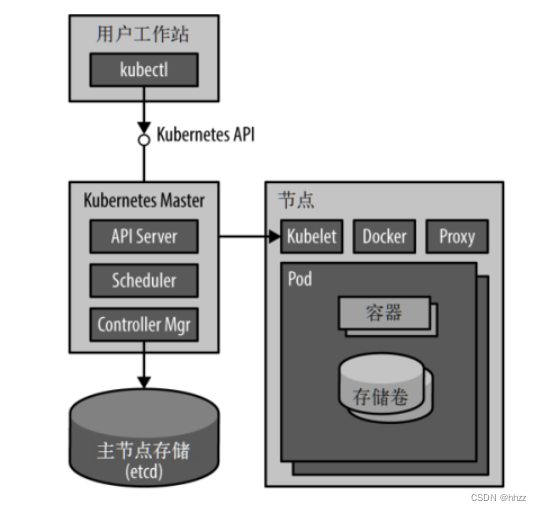
Docker+K8s基础(重要知识点总结)
目录 一、Docker的核心1,Docker引擎2,Docker基础命令3,单个容器运行多个服务进程4,多个容器运行多个服务进程5,备份在容器中运行的数据库6,在宿主机和容器之间共享数据7,在容器之间共享数据8&am…...

IDEA 关闭SpringBoot启动Logo/图标
一、环境 1、SpringBoot 2.6.4 Maven POM格式 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.6.4</version><relativePath/></parent> 2、IDE…...

提供话费充值接口 话费快充慢充/API独立接口,商城/小程序/公众号合作
话费充值接口文档 接口版本:1.0 ―、引言 文档概述 本文档提供话费充值接口规范说明,提供一整套的完整的接入示例(http 接口)供商户参 考,可以帮助商户开发人员快速完成接口开发与联调,实现与话费充值系统的交易互联。 公司官网…...
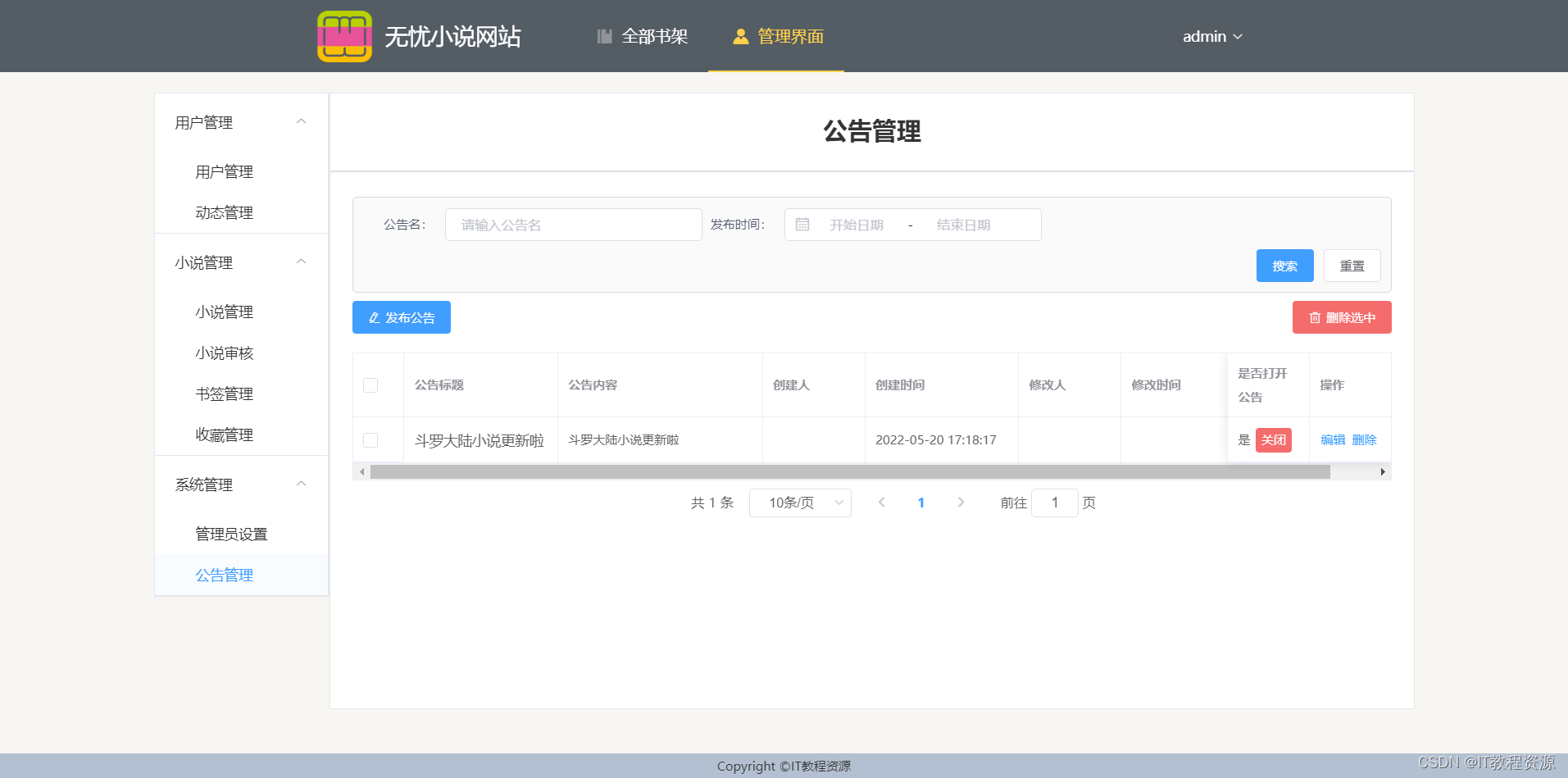
[N-133]基于springboot,vue小说网站
开发工具:IDEA 服务器:Tomcat9.0, jdk1.8 项目构建:maven 数据库:mysql5.7 系统分前后台,项目采用前后端分离 前端技术:vueelementUI 服务端技术:springbootmybatis-plus 本项…...
计算机网络:概述
0 学时安排及讨论题目 0.1讨论题目: CSMA/CD协议交换机基本原理ARP协议及其安全子网划分IP分片路由选择算法网络地址转换NATTCP连接建立和释放再论网络体系结构 0.2 本节主要内容 计算机网络在信息时代中的作用 互联网概述 互联网的组成 计算机网络在我国的发展 …...
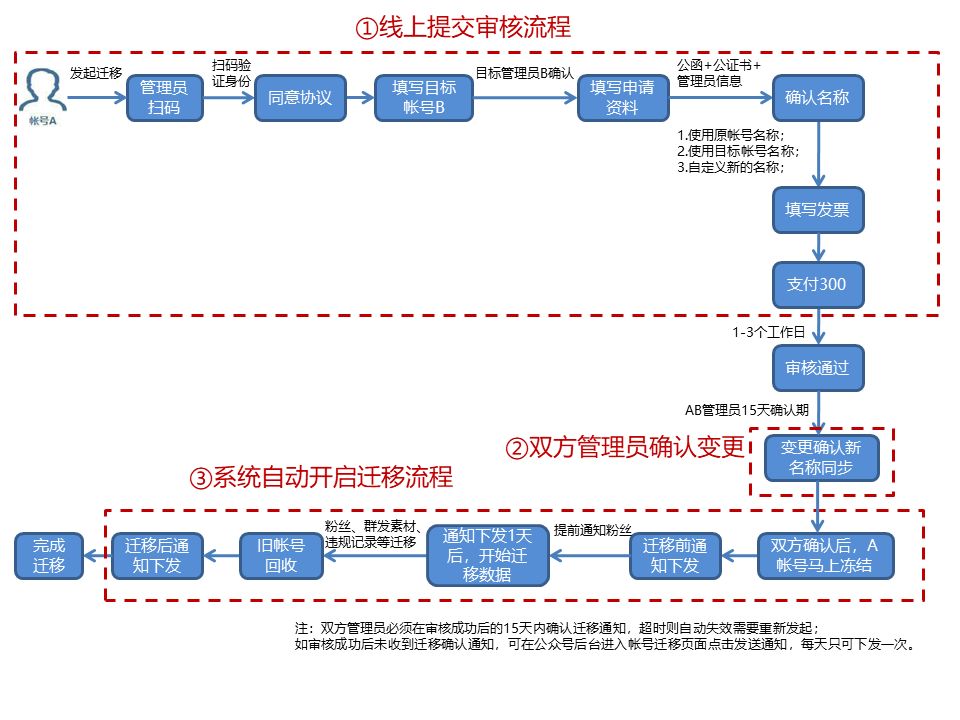
服务号怎么升级订阅号
服务号和订阅号有什么区别?服务号转为订阅号有哪些作用?首先我们要看一下服务号和订阅号的主要区别。1、服务号推送的消息没有折叠,消息出现在聊天列表中,会像收到消息一样有提醒。而订阅号推送的消息是折叠的,“订阅号…...

11.读取文件长度-fseek和ftell函数的使用
文章目录 简介1. 写入测试文件2. 读取文件长度 简介 主要讲使用fopen读取文件,配合使用fseek和ftell来读取文件长度。1. 写入测试文件 执行下方程序,使用fwrite函数写入40字节的数据,使其形成文件存入本地目录。#define _CRT_SECURE_NO_WARNI…...
视觉大模型DINOv2:自我监督学习的新领域
1 DINOv2 1.1 DINOv2特点 前段时间,Meta AI 高调发布了 Segment Anything(SAM),SAM 以交互式方式快速生成 Mask,并可以对从未训练过的图片进行精准分割,可以根据文字提示或使用者点击进而圈出图像中的特定…...

Java事务详解
一、事务的理解: 1、事务的特性: 1) 原子性(atomicity):事务是数据库的逻辑工作单位,而且是必须是原子工作单位,对于其数据修改,要么全部执行,要么全部不执行。 2) 一致性…...
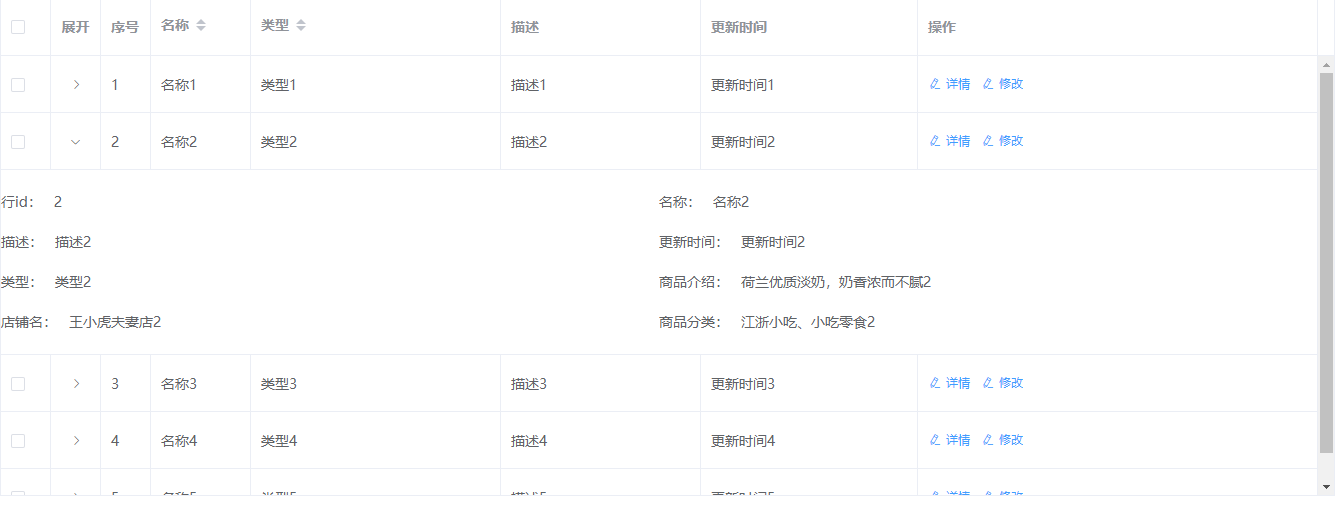
el-table实现展开当前行时收起上一行的功能
<el-tableref"tableRef":data"tableData":expand-row-keys"expandRowKeys":row-key"handleRowKey" // 必须指定 row-keyexpand-change"handleExpandChange" // 当用户对某一行展开或者关闭的时候会触发该事件> <…...
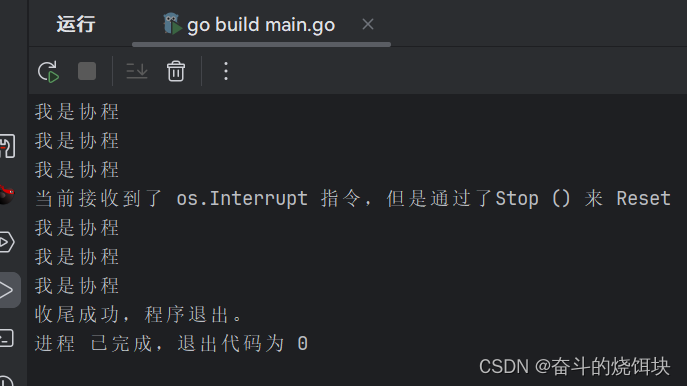
Go的优雅退出
Go优雅退出/停机以前主要通过signal来实现,当然现在也是通过signal来实现,只是从go 1.16开始,新增了更加友好的API: func NotifyContext(parent context.Context, signals ...os.Signal) (ctx context.Context, stop context.CancelFunc) 该…...

【KVM-6】KVM/QEMU软件栈
前言 大家好,我是秋意零。 👿 简介 🏠 个人主页: 秋意零🔥 账号:全平台同名, 秋意零 账号创作者、 云社区 创建者🧑 个人介绍:在校期间参与众多云计算相关比赛&#x…...

硬件知识2
原理图的检查: 网络悬浮 单端网络 电源悬浮(电源和地) 重复的位号 网络短路(电源和地) AD里面双击messages里面的错误项会直接进入到原理图和PCB…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
