数据结构(超详细讲解!!)第二十三节 树型结构
1.定义
树型结构是一类重要的非线性数据结构,是以分支关系定义的层次结构。是一种一对多的逻辑关系。
树型结构是结点之间有分支,并且具有层次关系的结构,它非常类似于自然界中的树。树结构在客观世界中是大量存在的,例如家谱、行政组织机构都可用树形象地表示。树在计算机领域中也有着广泛的应用,例如在编译程序中,用树来表示源程序的语法结构;在数据库系统中,可用树来组织信息;在分析算法的行为时,可用树来描述其执行过程。等等。
树(Tree)是n (n≥0)个结点的有限集T,T为空时称为空树,否则它满足以下条件:
(1) T中有且仅有一个结点K0没有前驱,称K0为树的根结点(Root)。
(2) 除根结点以外,其余结点有且仅有一个直接前驱。
(3) T中各结点可以有0个或多个后继。
(4) 当n ≥ 1时,除根结点以外,其余结点可分为m(m≥0)个互不相交的有限集合T1,T2,…,Tm。其中每个集合又构成一棵树,树T1,T2,…,Tm被称为根结点K0的子树(Subtree)。
树的逻辑结构表示数据之间的关系是一对多,或者多对一的关系。它的结构特点具有明显的层次关系,是一种十分重要的非线性的数据结构。
注:树的定义具有递归性,即树中还有树。
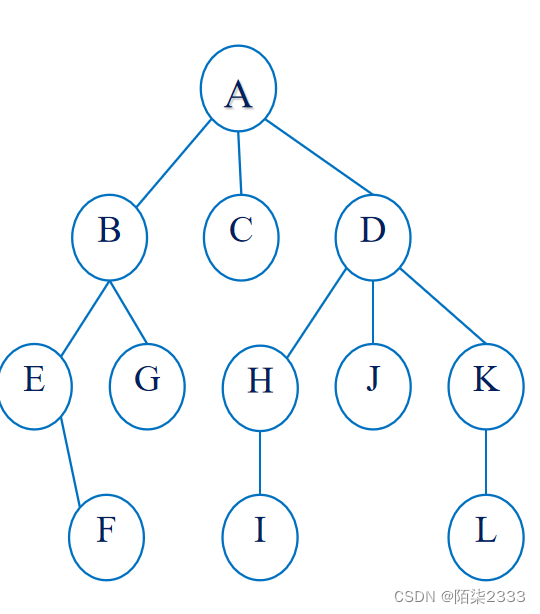
2.树的基本术语
1.父母、孩子与兄弟结点
结点的直接前驱结点称为双亲(parents)结点。
结点的直接后继结点称为孩子(child)结点。
拥有同一个父母结点的多个结点之间称为兄弟(sibling)结点。
结点的祖先(ancestor)是指从根结点到其双亲结点所经过的所有结点。(祖先结点)
结点的后代(descendant)是指该结点的所有孩子结点,以及孩子的孩子等。 (子孙结点)
祖先与后代的关系则是对父子关系的延伸,其定义了树中结点的纵向次序 。
2.度
结点的度(degree)是指结点所拥有子树的棵数。
度为零的结点称为叶子(leaf)或者终端结点
度不为零的结点称为分支结点或者非终端结点、非叶结点。
树的度是指树中各结点度的最大值。
3.结点层次、树的高度
结点的层次(level)属性反映结点处于树中的层次位置。
约定根结点的层次为1,其余结点的层次是其父母结点的层次加1.
树的高度(height)或深度(depth)是树中结点的最大层次数。
4.边、路径
设树中X结点是Y结点的父母结点,有序对(X,Y)称为连接这两个结点的分支,也称为边(edge)。
设(X0,X1,…,Xk-1)是由树中结点组成的一个序列,且(Xi,Xi+1)(0≤i<k-1)都是树中的边,则该序列称为X0到Xk-1的一条路径(path)。
路径长度(path length)为路径上的边数。
5.无序树、有序树
若把树中每个结点的各子树看成从左到右有次序的(即不能互换),则称该树为有序树(Ordered Tree);否则称为无序树(Unordered Tree)
如果规定k1和k2是兄弟,且k1在k2的左边,则k1的任一子孙都在k2的任一子孙的左边,则定义了树中结点的横向次序
6.森林
森林(Forest)是m(m≥0)棵互不相交树的集合。
给森林加上一个根结点就变成一棵树。
将树的根结点删除就变成森林。
3.树的表示方法
1.图形表示法

2.嵌套集合表示法

3.广义表表示法
根作为由子树森林组成的表的名字写在表的左边

4.凹入表示法(目录表示法)
4.抽象数据类型
ADT Tree{数据对象:D是具有相同属性的数据元素的集合。数据关系:若D为空集,则称为空树;若D仅含一个数据元素,则R为空集,否则R={H},H是如下二元关系:(1) 在D中存在唯一的称为根的数据元素root, 它在关系H下没有前驱。 (2) 除root以外, D中每个结点在关系H下都有且仅有一个前驱。 基本操作:void CreateTree(Tree *t,definition):初始条件:树t不存在。操作结果:按definition构造树t。int TreeEmpty(Tree t):初始条件:树t存在 。操作结果:若t为空树, 则返回1, 否则返回0。int TreeDepth(Tree t)初始条件:树t存在。操作结果:返回树t的深度。……
}
相关文章:

数据结构(超详细讲解!!)第二十三节 树型结构
1.定义 树型结构是一类重要的非线性数据结构,是以分支关系定义的层次结构。是一种一对多的逻辑关系。 树型结构是结点之间有分支,并且具有层次关系的结构,它非常类似于自然界中的树。树结构在客观世界中是大量存在的,例如家谱、…...

Python 日志记录器logging 百科全书 之 日志回滚
Python 日志记录器logging 百科全书 之 日志回滚 前言 在之前的文章中,我们学习了关于Python日志记录的基础配置。 本文将深入探讨Python中的日志回滚机制,这是一种高效管理日志文件的方法,特别适用于长时间运行或高流量的应用。 知识点&…...
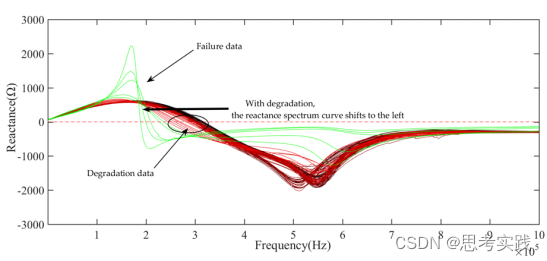
线圈寿命预测 数据集讲解
来自-郭师兄 1.这个是线圈数据的阻抗、电抗等数据,我想根据这个个数据进行线圈寿命预测也就是RUL预测,请问有什么思路吗。 最简单的思路: 数据通过某种方法进行压缩表征到一维再通过 同时需要标签。 确定一个特征 使用降维方法如同PCA来构…...

Flutter.源码分析.flutter/packages/flutter/lib/src/widgets/scroll_view.dart/GridView
Flutter.源码分析 GridView flutter/packages/flutter/lib/src/widgets/scroll_view.dart/GridView 李俊才 的个人博客:https://blog.csdn.net/qq_28550263 本文地址:https://blog.csdn.net/qq_28550263/article/details/134375048 本文提供 Flutter 框…...
IDEA 2022创建Spring Boot项目
首先点击New Project 接下来: (1). 我们点击Spring Initializr来创建。 (2). 填写项目名称 (3). 选择路径 (4). 选择JDK------这里笔者选用jdk17。 (5). java选择对应版本即可。 (6). 其余选项如无特殊需求保持默认即可。 然后点击Next。 稍等一会,…...
Python 框架学习 Django篇 (十) Redis 缓存
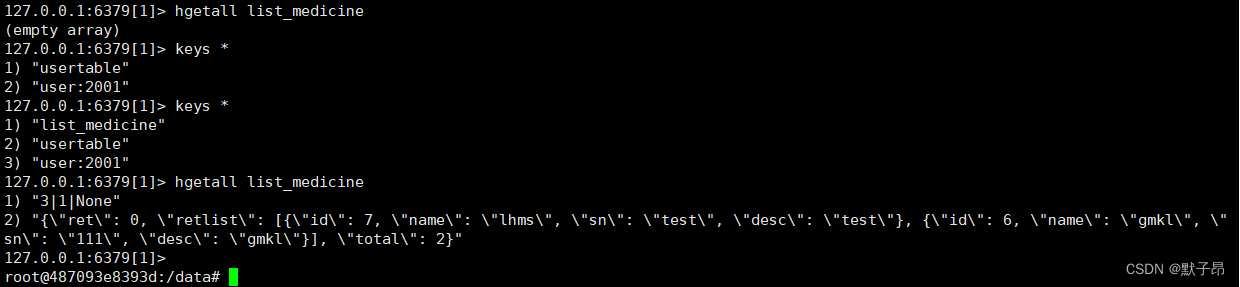
开发服务器系统的时候,程序的性能是至关重要的。经过我们前面框架的学习,得知一个请求的处理基本分为接受http请求、数据库处理、返回json数据,而这3个部分中就属链接数据库请求的响应速度最慢,因为数据库操作涉及到数据库服务处理…...

考研数学笔记:线性代数中抽象矩阵性质汇总
在考研线性代数这门课中,对抽象矩阵(矩阵 A A A 和矩阵 B B B 这样的矩阵)的考察几乎贯穿始终,涉及了很多性质、运算规律等内容,在这篇考研数学笔记中,我们汇总了几乎所有考研数学要用到的抽象矩阵的性质…...

C语言--假设共有鸡、兔30只,脚90只,求鸡、兔各有多少只
一.题目描述 假设共有鸡、兔30只,脚90只,求鸡、兔各有多少只? 二.思路分析 本题是一个典型的穷举法例题,而穷举法,最重要的就是条件判断。⭐⭐ 本题中的条件很容易发现: 假设鸡有x只,兔有y只…...
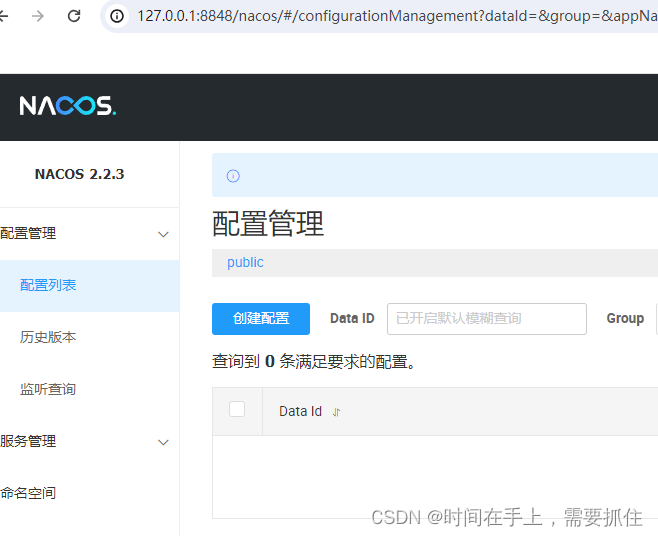
nacos适配达梦数据库
一、下载源码 源码我直接下载gitee上nacos2.2.3的,具体链接:https://gitee.com/mirrors/Nacos/tree/2.2.3,具体如下图: 二、集成达梦数据库驱动 解压源码包,用idea打开源码,等idea和maven编译完成ÿ…...
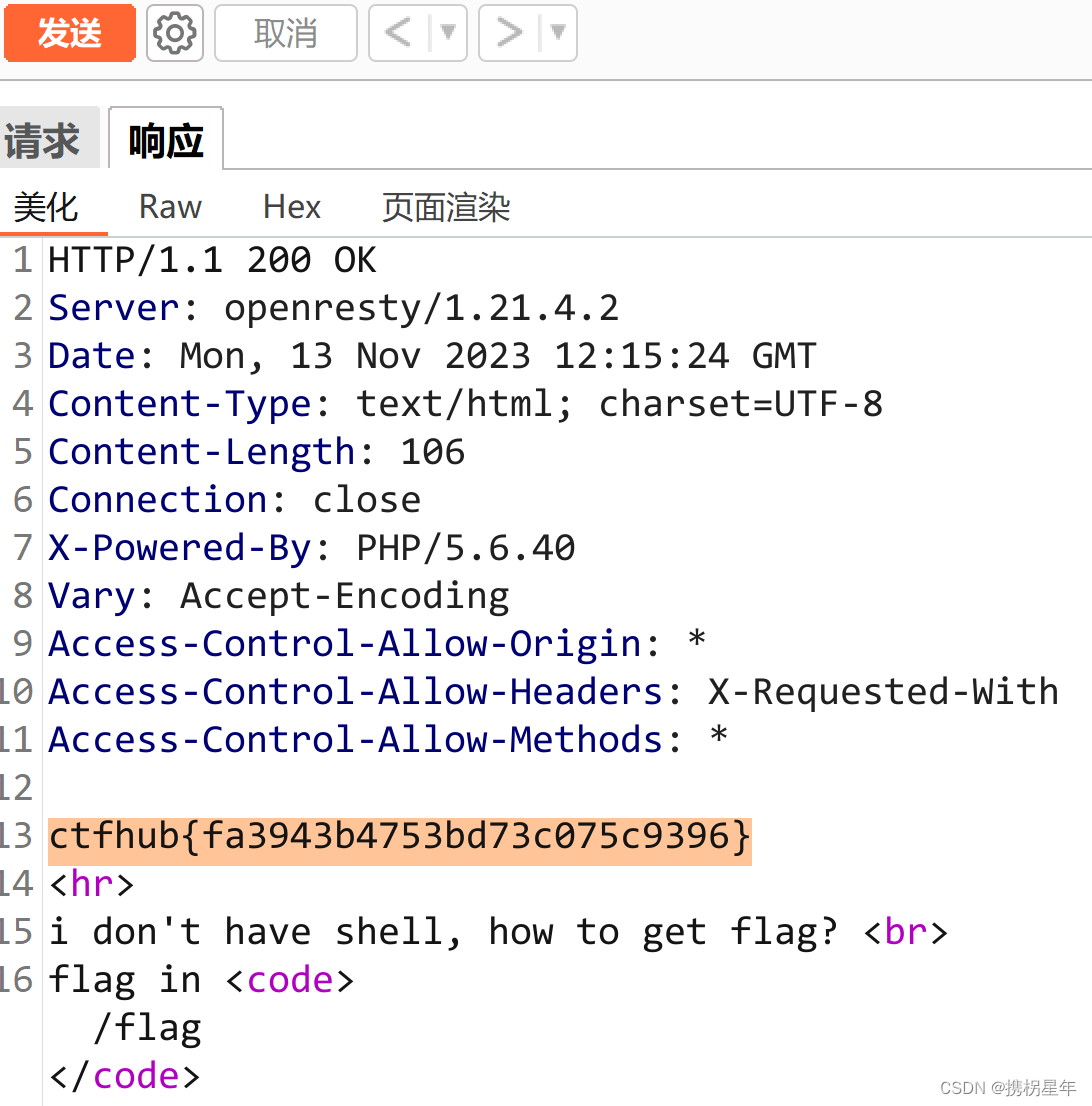
CTFhub-RCE-读取源代码
源代码: <?php error_reporting(E_ALL); if (isset($_GET[file])) { if ( substr($_GET["file"], 0, 6) "php://" ) { include($_GET["file"]); } else { echo "Hacker!!!"; } } else {…...
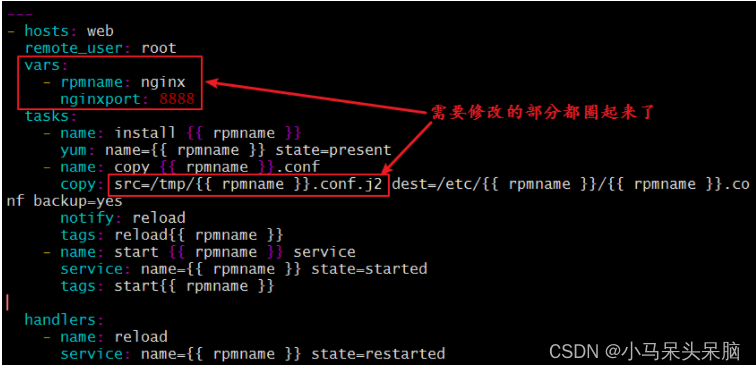
Ansible playbook详解
playbook是ansible用于配置,部署,和被管理被控节点的剧本 playbook常用的YMAL格式:(文件名称以 .yml结尾) 1、文件的第一行应该以 "---" (三个连字符)开始,表明YMAL文件的开始。 2、在同一…...

Linux编辑器:vim的简单介绍及使用
目录 1.什么是vim 2.vim的基本概念 3.vim 的基本操作 4. 各模式下的命令集 4.1 正常模式命令集 4.2 末行模式命令集 5.补充 5.1 vim支持多文件编辑 5.2 vim 的配置 1.vim 配置原理 2. 常用简单配置选项: 3. 使用插件 1.什么是vim Vim 是从 vi 发展出…...
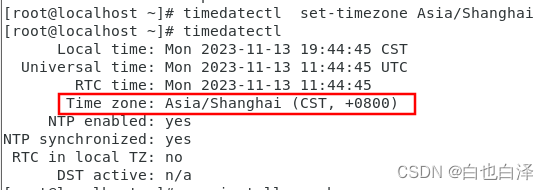
Redhat7查看时区、修改时区
问题: 安装好redhat7之后,发现时间和物理机上面的网络时间不一致,于是查看本着修改时间的目的,却发现原来是时区的问题。 解决步骤: 查看时区状态信息 timedatectl修改时区到亚洲/上海 timedatectl set-timezone A…...

OpenCV踩坑笔记使用笔记入门笔记整合SpringBoot笔记大全
springboot开启摄像头抓拍照片并上传实现&问题记录 NotAllowedErrot: 请求的媒体源不能使用,以下情况会返回该错误: 当前页面内容不安全,没有使用HTTPS没有通过用户授权NotFoundError: 没有找到指定的媒体通道NoReadableError: 访问硬件设备出错Ov…...
)
【数据结构】栈和队列的模拟实现(两个方式实现)
前言 💓作者简介: 加油,旭杏,目前大二,正在学习C,数据结构等👀 💓作者主页:加油,旭杏的主页👀 ⏩本文收录在:再识C进阶的专栏…...

OpenCV+相机校准和3D重建
相机校准至少需要10个测试图案,所需的重要输入数据是3D现实世界点集以及图像中这些点的相应2D坐标。3D点称为对象点,而2D图像点称为图像点。 准备工作 除了棋盘,我们还可以使用圆形网格。 在这种情况下,我们必须使用函数cv.find…...

2023.11.14-hive之表操作练习和文件导入练习
目录 需求1.数据库基本操作 需求2. 默认分隔符案例 需求1.数据库基本操作 -- 1.创建数据库test_sql,cs1,cs2,cs3 create database test_sql; create database cs1; create database cs2; create database cs3; -- 2.1删除数据库cs2 drop database cs2; -- 2.2在cs3库中创建…...
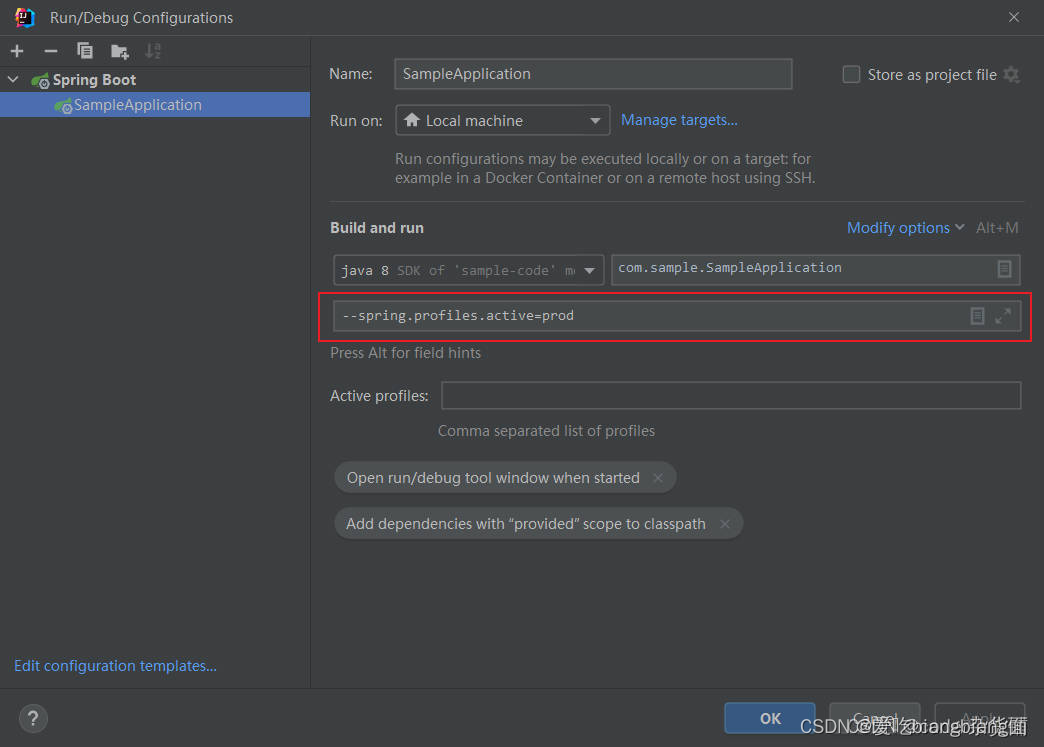
idea2023启动springboot项目如何指定配置文件
方法一: 方法二: 举例:...
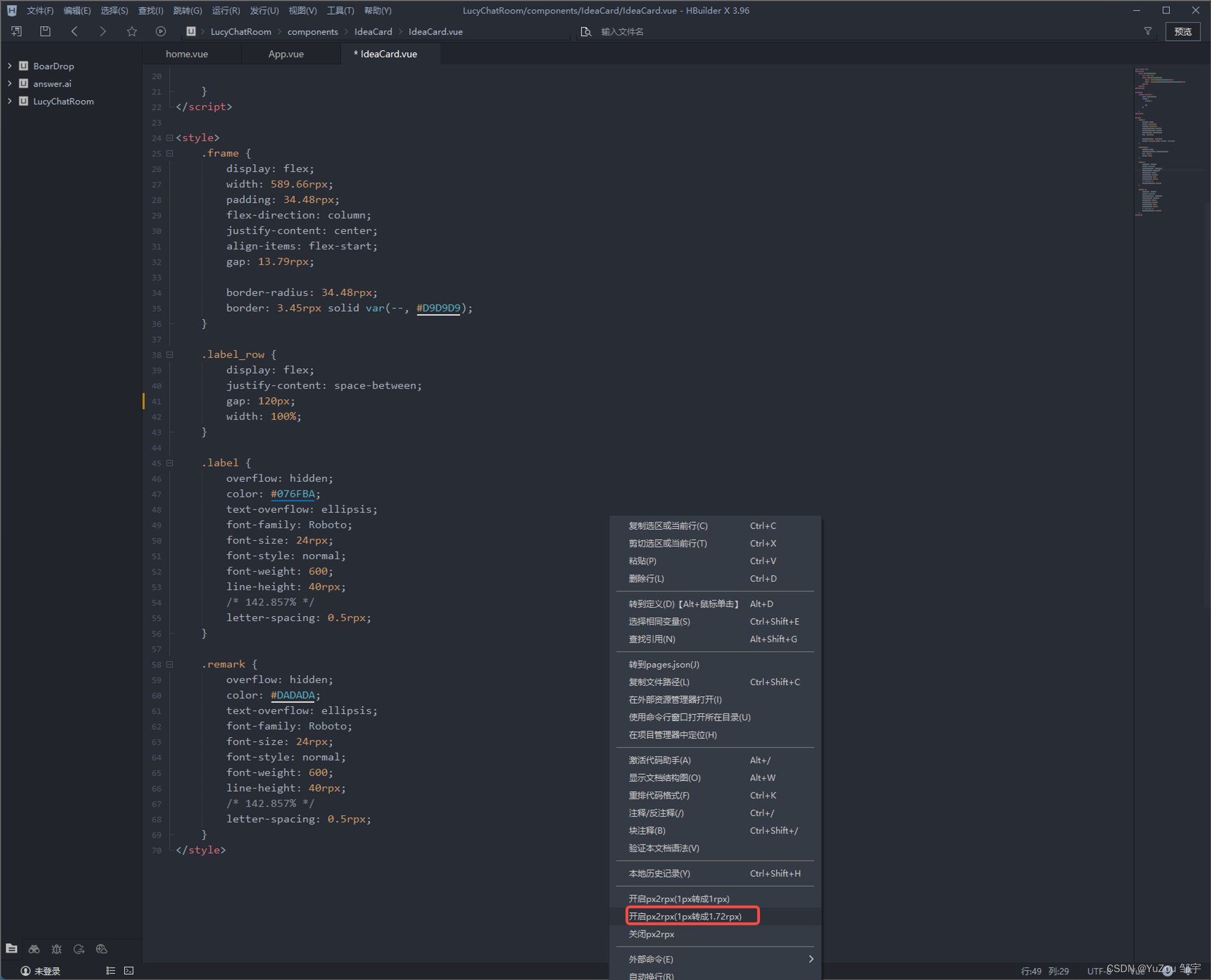
在 uniapp 中 一键转换单位 (px 转 rpx)
在 uniapp 中 一键转换单位 px 转 rpx Uni-app 官方转换位置利用【px2rpx】插件Ctrl S一键全部转换下载插件修改插件 Uni-app 官方转换位置 首先在App.vue中输入这个: uni.getSystemInfo({success(res) {console.log("屏幕宽度", res.screenWidth) //屏…...

SQL对数据进行去重
工作中使用SQL对数据进行处理计算时可能会遇到这样的问题;读取的表数据会有重复,或者我们关注的几个字段的数据会有重复,直接使用原表数据会引起计算结果不准或者做表连接时产生笛卡尔积。 本文记录使用SQL进行数据去重的几种算法。 distinc…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
