[100天算法】-不同路径 III(day 75)
题目描述
在二维网格 grid 上,有 4 种类型的方格:1 表示起始方格。且只有一个起始方格。
2 表示结束方格,且只有一个结束方格。
0 表示我们可以走过的空方格。
-1 表示我们无法跨越的障碍。
返回在四个方向(上、下、左、右)上行走时,从起始方格到结束方格的不同路径的数目。每一个无障碍方格都要通过一次,但是一条路径中不能重复通过同一个方格。示例 1:输入:[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
输出:2
解释:我们有以下两条路径:
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)
示例 2:输入:[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
输出:4
解释:我们有以下四条路径:
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)
示例 3:输入:[[0,1],[2,0]]
输出:0
解释:
没有一条路能完全穿过每一个空的方格一次。
请注意,起始和结束方格可以位于网格中的任意位置。提示:1 <= grid.length * grid[0].length <= 20
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/unique-paths-iii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
从起始格子开始,尝试每一个 0 空格。当走到 2 时,如果此时网格没有还没走过的空格,说明这是一条可行的路径。也就是说我们需要用一个方式来标志已经走过的空格,可以把格子设为 -1,回溯时需要把格子重新设置为 0,不影响其他路径的尝试。
当我们走到 2 时,如何判断网格中是否还有未走过的空格?
每次都去遍历整个网格的话,时间复杂度太高。我们可以在开始先统计网格中一共有多少个可以走的格子,每走过一个格子计数器就减一。
复杂度
- 时间复杂度:$O(4^{mn})$, m, n 分别是网格的长宽。找到起始格子和统计空格用了 $O(mn)$,递归的时间复杂度 $O(4^{mn})$,网格一共有 $mn$ 个格子,每个格子有 4 个方向可以走。
- 空间复杂度:递归栈的最大空间 $O(m*n)$。
p.s. 下方代码是我看错题了,求了所有路径。实际上只需要一个计数器来记录路径数,不消耗额外空间。
代码
JavaScript Code
/*** @param {number[][]} grid* @return {number}*/
var uniquePathsIII = function (grid) {const offsets = [[-1, 0],[1, 0],[0, -1],[0, 1],];const ans = [];const dfs = (grid, x, y, spaceCnt, path) => {if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length) return;if (grid[x][y] === 2) {spaceCnt === 0 && ans.push([...path]);return;}if (grid[x][y] === -1) return;grid[x][y] = -1; // mark// recursionfor (const [ox, oy] of offsets) {// p.s. 如果 (x+ox, y+oy) 不在网格中或者是障碍的话,也可以提前剪枝。dfs(grid, x + ox, y + oy, spaceCnt - 1, [...path, [x, y]]);}grid[x][y] = 0; // backtrack};let startPos = {};const init = grid => {let spaceCnt = 1; // 起始方格也是要走的一个格子for (let x = 0; x < grid.length; x++) {for (let y = 0; y < grid[x].length; y++) {if (grid[x][y] === 1) startPos = { x, y };if (grid[x][y] === 0) spaceCnt++;}}return spaceCnt;};// 统计要走的格子总数const spaceCnt = init(grid);dfs(grid, startPos.x, startPos.y, spaceCnt, []);return ans.length;
};相关文章:
)
[100天算法】-不同路径 III(day 75)
题目描述 在二维网格 grid 上,有 4 种类型的方格:1 表示起始方格。且只有一个起始方格。 2 表示结束方格,且只有一个结束方格。 0 表示我们可以走过的空方格。 -1 表示我们无法跨越的障碍。 返回在四个方向(上、下、左、右&#…...

【学习笔记】[CCO2021] Travelling Merchant
不难看出,这是一道在图上 D P DP DP的问题。设 f i f_i fi表示从 i i i出发,能够不停的游走下去,所需要的最少的初始资产。可以写出粗略的转移: f u min ( f u , max ( f v − p i , r i ) ) f_u\min(f_u,\max(f_v-p_i,r…...

【终端】记录mbedtls库的重新安装
记录mbedtls库的在终端上重新安装的步骤 ffmpeg -version dyld[17464]: Library not loaded: /usr/local/opt/mbedtls/lib/libmbedcrypto.14.dylibReferenced from: /usr/local/Cellar/librist/0.2.7_3/lib/librist.4.dylibReason: tried: /usr/local/opt/mbedtls/lib/libmbed…...
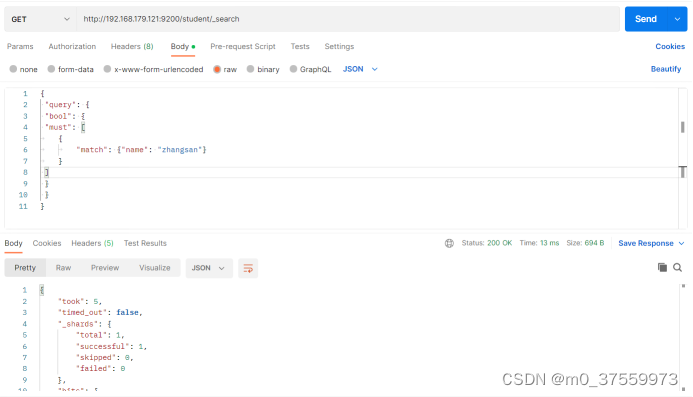
ElasticSearch简单操作
目录 1.单机部署 1.1 解压软件 1.2 创建软链接 1.3 修改配置文件 1.4 配置环境变量 1.5 后台启动 2.配置分词器 2.1 安装IK分词器 2.2 ES 扩展词汇 3.常用操作 3.1 索引 3.1.1 创建索引 3.1.2 查看所有索引 3.1.3 查看单个索引 3.1.4 删除索引 3.2.文档 3.2.1…...
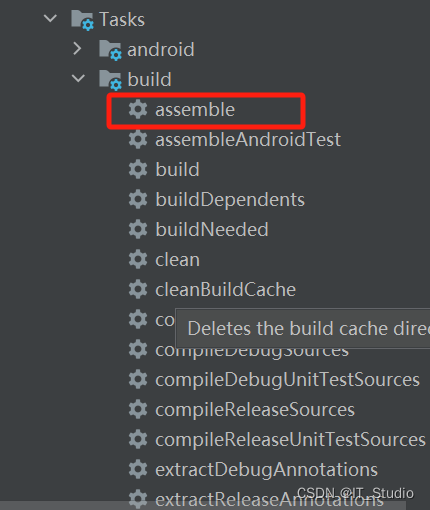
android studio新版本gradle Tasks找不到assemble
最近需要打包arr,但android studio新版本为了加快编译速度,取消了gradle下的assemble任务,网上还没有博主更新解决方案,因此一直找不到解决方案,后来尝试如下操作才解决,方便后来者解决。 先将这里勾选上&…...

uniapp 小程序 身份证 和人脸视频拍摄
使用前提: 已经在微信公众平台的用户隐私协议,已经选择配置“摄像头,录像”等权限 开发背景:客户需要使用带有拍摄边框的摄像头 ,微信小程序的方法无法支持,使用camera修改 身份证正反面: <…...

飞腾ARM UOS编译Qt 5.15.2源码及Qt Creator
背景 在 ARM 架构下,UOS 系统,需要使用 Qt 5.15.2 版本环境,所以只能通过源码编译的形式进行 Qt 环境的部署。 软硬件相关信息: 处理器: 飞腾 FT-2000 4 核制造商: Phytium架构: aarch 64家族: ARMv 8系统:UOS V 20…...
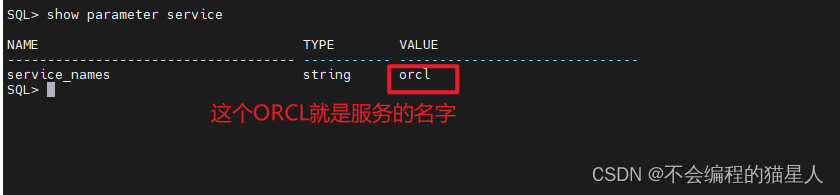
Oracle(2-2)Oracle Net Architecture
文章目录 一、基础知识1、Oracle Net Connections Oracle网络连接2、C/S Application Connection C/S应用程序连接3、OSI Communication Layers OSI通信层4、Oracle Protocol Support Oracle协议支持5、B/S Application Connections B/S应用程序连接6、TwoTypes JDBC Drivers 两…...

高速高精运动控制,富唯智能AI边缘控制器助力自动化行业变革
随着工业大数据时代的到来,传统控制与决策方式无法满足现代数字化工厂对工业大数据分析与决策的需求,AI边缘控制器赋能现代化智慧工厂,实现工业智造与行业变革。 富唯智能AI边缘控制器,基于x86架构的IPC形态产品,通过…...
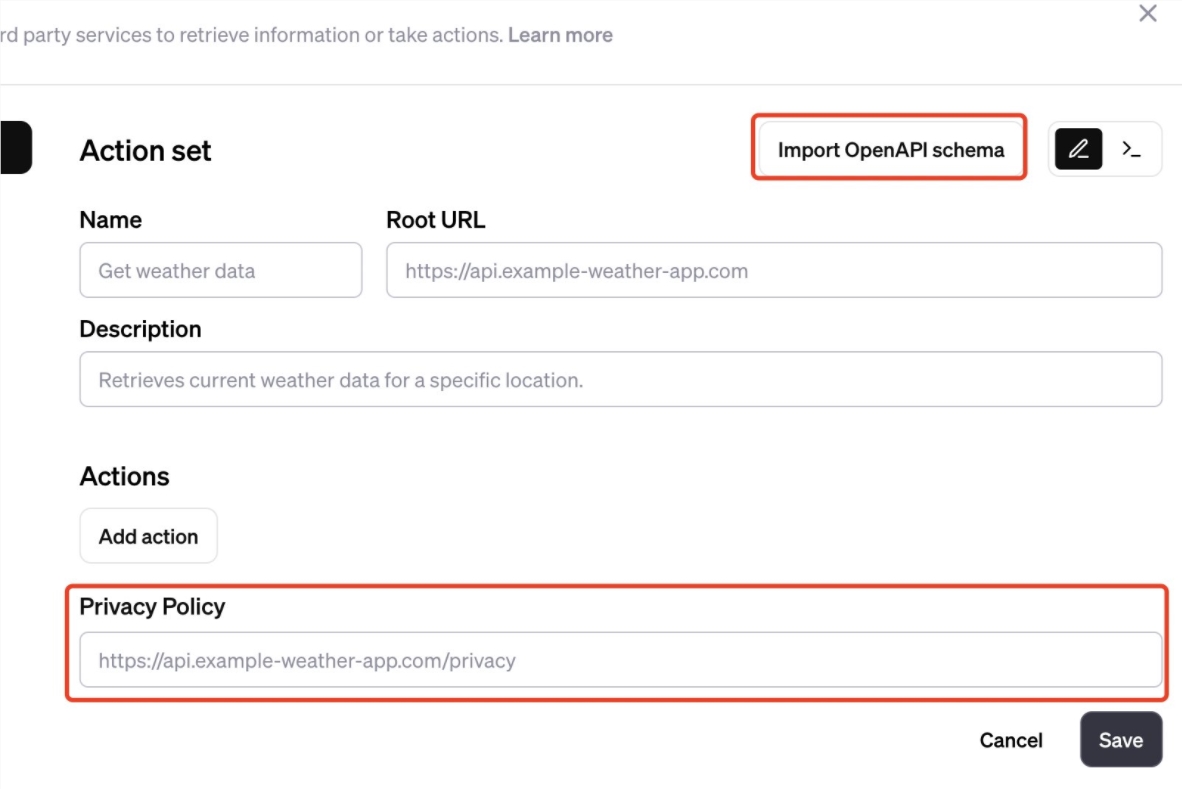
GPTS应用怎么创建?GPTS无法创建应用很卡怎么办
在首届开发者大会上,OpenAI宣布推出了GPTs功能,也就是GPT Store,类似App Store的应用商店,任何用户都可以去参与创建应用。那么GPTS应用该如何创建?碰到应用无法创建很卡怎么办呢?下面就为大家带来GPTS应用创建图文教程…...

目标检测YOLO实战应用案例100讲-基于无人机的运动目标检测
目录 前言 国内外研究现状 2运动目标检测相关理论基础 2.1 运动目标检测算法...

东莞松山湖数据中心|莞服务器托管的优势
东莞位于珠江三角洲经济圈,交通便利,与广州、深圳等大城市相邻,而且东莞是中国重要的制造业基地,有众多的制造业和科技企业集聚于此,随着互联网和数字化时代的到来,企业都向数字化转型,对于信息…...

时间序列预测实战(十五)PyTorch实现GRU模型长期预测并可视化结果
往期回顾:时间序列预测专栏——包含上百种时间序列模型带你从入门到精通时间序列预测 一、本文介绍 本文讲解的实战内容是GRU(门控循环单元),本文的实战内容通过时间序列领域最经典的数据集——电力负荷数据集为例,深入的了解GRU的基本原理和…...

探索STM32系列微控制器的特性和性能
STM32系列微控制器是意法半导体(STMicroelectronics)公司开发的一款强大的嵌入式微控制器系列。该系列微控制器以其丰富的特性和卓越的性能,成为了嵌入式系统开发领域的首选。本文将深入探索STM32系列微控制器的特性和性能,并结合…...
数据结构(超详细讲解!!)第二十三节 树型结构
1.定义 树型结构是一类重要的非线性数据结构,是以分支关系定义的层次结构。是一种一对多的逻辑关系。 树型结构是结点之间有分支,并且具有层次关系的结构,它非常类似于自然界中的树。树结构在客观世界中是大量存在的,例如家谱、…...

Python 日志记录器logging 百科全书 之 日志回滚
Python 日志记录器logging 百科全书 之 日志回滚 前言 在之前的文章中,我们学习了关于Python日志记录的基础配置。 本文将深入探讨Python中的日志回滚机制,这是一种高效管理日志文件的方法,特别适用于长时间运行或高流量的应用。 知识点&…...
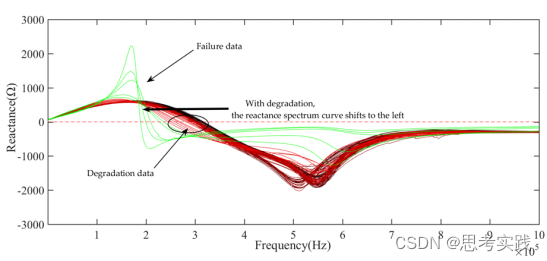
线圈寿命预测 数据集讲解
来自-郭师兄 1.这个是线圈数据的阻抗、电抗等数据,我想根据这个个数据进行线圈寿命预测也就是RUL预测,请问有什么思路吗。 最简单的思路: 数据通过某种方法进行压缩表征到一维再通过 同时需要标签。 确定一个特征 使用降维方法如同PCA来构…...

Flutter.源码分析.flutter/packages/flutter/lib/src/widgets/scroll_view.dart/GridView
Flutter.源码分析 GridView flutter/packages/flutter/lib/src/widgets/scroll_view.dart/GridView 李俊才 的个人博客:https://blog.csdn.net/qq_28550263 本文地址:https://blog.csdn.net/qq_28550263/article/details/134375048 本文提供 Flutter 框…...
IDEA 2022创建Spring Boot项目
首先点击New Project 接下来: (1). 我们点击Spring Initializr来创建。 (2). 填写项目名称 (3). 选择路径 (4). 选择JDK------这里笔者选用jdk17。 (5). java选择对应版本即可。 (6). 其余选项如无特殊需求保持默认即可。 然后点击Next。 稍等一会,…...
Python 框架学习 Django篇 (十) Redis 缓存
开发服务器系统的时候,程序的性能是至关重要的。经过我们前面框架的学习,得知一个请求的处理基本分为接受http请求、数据库处理、返回json数据,而这3个部分中就属链接数据库请求的响应速度最慢,因为数据库操作涉及到数据库服务处理…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...
