线性代数本质系列(一)向量,线性组合,线性相关,矩阵
本系列文章将从下面不同角度解析线性代数的本质,本文是本系列第一篇
向量究竟是什么?
向量的线性组合,基与线性相关
矩阵与线性相关
矩阵乘法与线性变换
三维空间中的线性变换
行列式
逆矩阵,列空间,秩与零空间
克莱姆法则
非方阵
点积与对偶性
叉积
以线性变换眼光看叉积
基变换
特征向量与特征值
抽象向量空间
快速计算二阶矩阵特征值
张量,协变与逆变和秩
文章目录
- 前言
- 向量究竟是什么?
- 向量的线性组合,基于线性相关
- 矩阵与线性相关
前言
天道中丁元英说过一句话:佛说,看山是山,看水是水,普通大众寄情山水之间时,如神一般的丁元英却早已看透文化属性;今天我们不研究这么高深的哲学,回到线性代数,向量,矩阵对于我来讲只不过是一堆数字,但切换到神的视角,他们却是几何与变换,瞬间让线性代数变得更加立体生动,今天我们就从几何的角度去探索线性代数的本质。
向量究竟是什么?
通过“究竟”一词可见,对于向量的含义,存在不同的解释,目前,主要有三种解释:
⑴从物理学家的角度看:向量是指向空间的箭头,它有两个属性:长度和方向,无论怎么移动他都是同一个向量。

⑵从计算机角度看:向量是有序的数字列表,例如对于房价预测而言,房子的面积,房间数就可以看作是一个向量: [ 80 4 ] \begin{bmatrix}80\\4\end{bmatrix} [804]
⑶从数学家的角度看:向量可以是任何东西,只要具有向量和向量加法,标量和向量乘法这两种运算规律的事务都可以看作是向量
v ⃗ + w ⃗ \vec{v} +\vec{w} v+w
2 v ⃗ 2\vec{v} 2v
例如:
[ − 4 10 ] + [ 20 1 ] = [ 16 11 ] \begin{equation*} \begin{bmatrix} -4\\ 10 \end{bmatrix} +\begin{bmatrix} 20\\ 1 \end{bmatrix} =\begin{bmatrix} 16\\ 11 \end{bmatrix} \end{equation*} [−410]+[201]=[1611]
2 ∗ [ 80 4 ] = [ 160 8 ] \begin{equation*} 2*\begin{bmatrix} 80\\ 4 \end{bmatrix} =\begin{bmatrix} 160\\ 8 \end{bmatrix} \end{equation*} 2∗[804]=[1608]
由于数学家的角度过于抽象,这就出现了开头讲的,换个角度看问题,从几何角度看待线性代数,对于向量而言,就是在特定坐标系下,以原点为起点,指向某个方向的箭头:
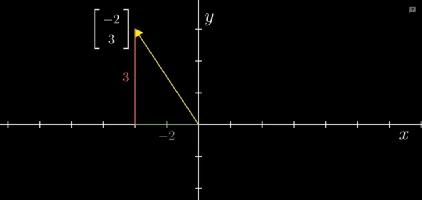
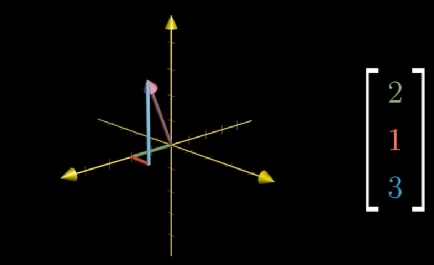
现在已经有了使用几何方式表达向量的方法,下面让我们从几何角度重新审视向量的两种运算:
对于 v ⃗ + w ⃗ \vec{v} +\vec{w} v+w而言,移动w到v的末尾,连接v的头和w的尾就是结果向量。
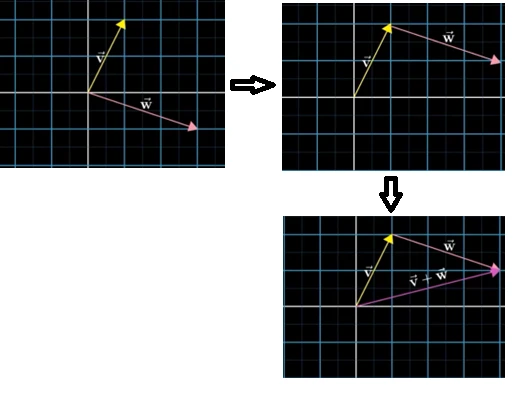
对于 2 v ⃗ 2\vec{v} 2v而言,向量的方向不变,长度变为原来的两倍,如果标量是小数,则是缩小向量的长度,如果是负数,则是反方向缩放向量的长度。
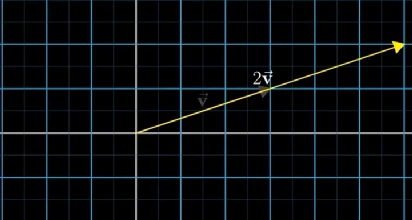
向量的线性组合,基于线性相关
基向量:
“单位“是数学中必不可少的概念,缺少单位,数字变得毫无意义,同样,对于使用几何表示向量而言,也有存在单位的概念,这就是“基向量”,它代表指向x,y轴,长度为1的向量,我们分别用 i ⃗ \vec{i} i, j ⃗ \vec{j} j表示。
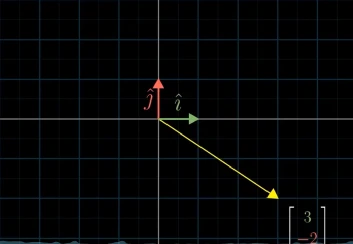
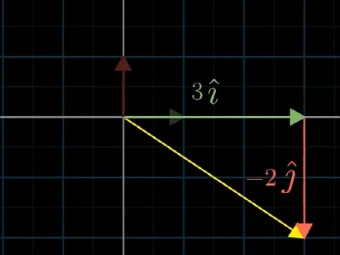
有了基的概念后,向量的表示可以转换成以基为参照,例如向量 [ 3 − 2 ] \begin{bmatrix} 3\\ -2 \end{bmatrix} [3−2],则可以表示成: 3 ∗ i ⃗ + 2 ∗ j ⃗ 3*\vec{i} +2*\vec{j} 3∗i+2∗j
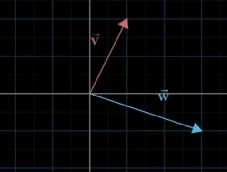
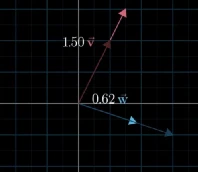
这里需要注意,前面我们选择指向x,y轴,且长度为1的向量作为基向量,但也可以选择不同的基,不同的基代表不同的坐标系,则对于一个向量而言,它代表不同的几何意义,例如,选择下面的v和w向量作为基向量时,向量 [ 1.5 − 0.62 ] \begin{bmatrix} 1.5\\ -0.62 \end{bmatrix} [1.5−0.62]代表的几何形状与 i ⃗ \vec{i} i, j ⃗ \vec{j} j为基向量时的形状是不一样的。
向量线性组合:
无论选择什么样的基向量,向量都可以写成更一般的形式: a v ⃗ + b w ⃗ a\vec{v} +b\vec{w} av+bw我们称为向量的线性组合,a,b是标量,也称为缩放因子,v和w是向量,选择不同的缩放因子,向量的线性组合可以表示整个向量空间,也就是生成的向量可以到达平面中所有点。
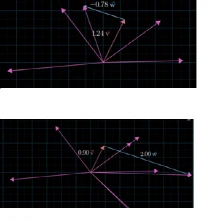
但如果两个向量恰好共线时,则向量组合后的结果向量只能落在该直线上,我们称共线的两个向量是线性相关的,否则是线性无关。
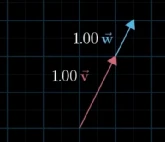
更特殊地,当这两个向量都是0向量时,则向量组合后的结果向量只能落在原点上。
概括一下,所有可以被给定向量,用线性组合来表示的那些向量的集合,被称为给定向量张成的空间,两个不共线的向量,在二维空间中,其线性组合所张成的空间是整个二维空间;而在三维空间中,其张成的空间是三维空间中的一个面。
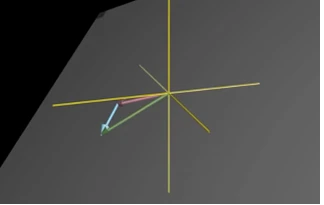
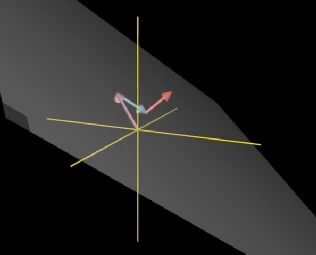
在三维空间中,三个向量的线性组合,如果其中一个向量在另两个向量张成的平面内,我们称该向量与其他两个向量线性相关,这三个向量的线性组合仍然是一个平面,只有三个向量互不线性相关时,那么这三个向量的线性组合才能张成整个三维空间。
矩阵与线性相关
矩阵:
先说结论:前面讲的向量可以视为一种带箭头的几何结构,那么矩阵就可以视为一种对几何的变换。
在线性代数中,变换是一种函数,将输入映射成输出,输入是向量,输出也是向量,同理,当输入是矩阵时,可以把矩阵分解成多个向量,那么输出也就是矩阵,变换有很多种,线性代数中只讨论线性变换,线性变换要求,任意直线变换后仍然是直线,且原点位置变换后保持不变,从几何角度看,线性变换就是拉伸,缩放,旋转。
下图变换后,直线变弯曲了,所以是非线性变换
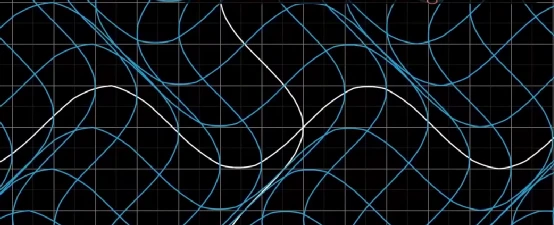
下图变换后,原点位置变了,所以属于非线性变换
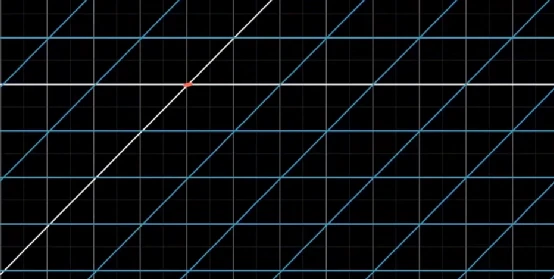
那我们如何求一个向量经过变换后的向量坐标呢?假设现有一个向量,在原始坐标系下可以表示成: v ⃗ = ( − 1 ) i ⃗ + 2 ∗ j ⃗ \vec{v} =( -1)\vec{i} +2*\vec{j} v=(−1)i+2∗j 。
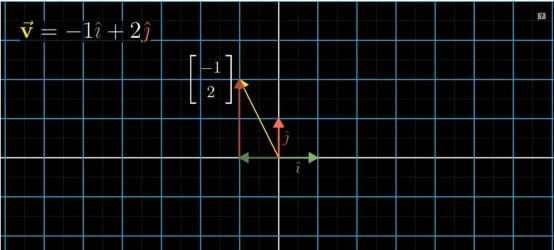
现在对向量v施加一个线性变换,根据线性变换的特性,变换后,网格仍然平行且间隔均等,假设两个基向量变换后的坐标如下图所示,向量v与两个基向量经过相同的变换变成新的基向量,那么,向量v经过变换后的向量仍然可以表示成:
v ⃗ t r a n s f o r m e d = ( − 1 ) i ⃗ t r a n s f o r m e d + 2 ∗ j t r a n s f o r m e d \begin{equation*} \vec{v}{}_{transformed} =( -1)\vec{i}{}_{transformed} +2*j{}_{transformed} \end{equation*} vtransformed=(−1)itransformed+2∗jtransformed
只不过基向量变成了变换后的基向量。
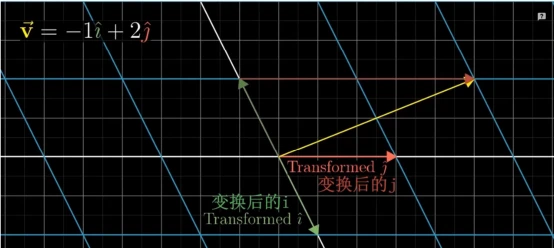
如上图
i ⃗ t r a n s f o r m e d = [ 1 − 2 ] \vec{i}{}_{transformed} =\begin{bmatrix} 1\\ -2 \end{bmatrix} itransformed=[1−2], j ⃗ t r a n s f o r m e d = [ 3 0 ] \vec{j}{}_{transformed} =\begin{bmatrix} 3\\ 0 \end{bmatrix} jtransformed=[30]
变换后的v就等于: v ⃗ = ( − 1 ) [ 1 − 2 ] + 2 ∗ [ 3 0 ] = [ 5 2 ] \vec{v} =( -1)\begin{bmatrix} 1\\ -2 \end{bmatrix} +2*\begin{bmatrix} 3\\ 0 \end{bmatrix} =\begin{bmatrix} 5\\ 2 \end{bmatrix} v=(−1)[1−2]+2∗[30]=[52]
也就是说,如果我们知道两个基向量变换后的向量,那么求任何一个向量经过变换后的向量的过程可以用下图所表示:
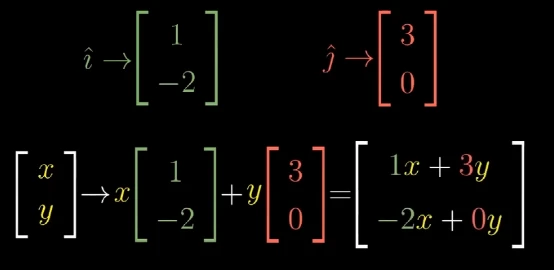
更进一步的,我们将两个基向量变换后的坐标向量用矩阵的形式组织起来,这个矩阵就是线性变换矩阵T。
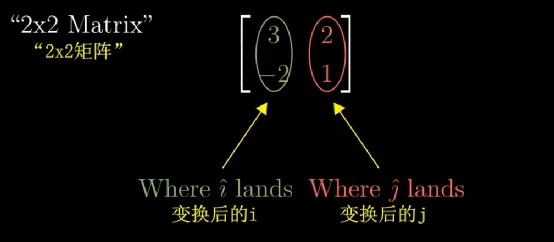
对于任意一个向量A,例如, [ 7 2 ] \begin{bmatrix} 7\\ 2 \end{bmatrix} [72],求该线性变换T对该向量的作用时,只需要用矩阵与向量相乘即可: A t r a n s f o r m e d = [ 3 2 − 2 1 ] [ 7 2 ] = 7 [ 3 − 2 ] + 2 [ 2 1 ] A_{transformed} =\begin{bmatrix} 3 & 2\\ -2 & 1 \end{bmatrix}\begin{bmatrix} 7\\ 2 \end{bmatrix} =7\begin{bmatrix} 3\\ -2 \end{bmatrix} +2\begin{bmatrix} 2\\ 1 \end{bmatrix} Atransformed=[3−221][72]=7[3−2]+2[21]。
如果换个视角,反过来看,如果给出一个矩阵乘法: [ 3 2 − 2 1 ] [ 7 2 ] \begin{bmatrix} 3 & 2\\ -2 & 1 \end{bmatrix}\begin{bmatrix} 7\\ 2 \end{bmatrix} [3−221][72],我们可以把矩阵第一列 [ 3 − 2 ] \begin{bmatrix} 3\\ -2 \end{bmatrix} [3−2]当作新的基向量 i ⃗ \vec{i} i,把矩阵的第二列 [ 2 1 ] \begin{bmatrix} 2\\ 1 \end{bmatrix} [21]当作新的基向量 j ⃗ \vec{j} j,根据向量的几何表示,向量 [ 7 2 ] \begin{bmatrix} 7\\ 2 \end{bmatrix} [72]用新的基向量表成: i ⃗ \vec{i} i向正方向放大7倍, j ⃗ \vec{j} j向正方向放大2倍,将变换后的向量相加就形成了结果向量。

再举个例子,看看逆时针旋转90度的变换矩阵是什么, i ⃗ \vec{i} i由 [ 1 0 ] \begin{bmatrix} 1\\ 0 \end{bmatrix} [10]变成 [ 0 1 ] \begin{bmatrix} 0\\ 1 \end{bmatrix} [01], j ⃗ \vec{j} j由 [ 0 1 ] \begin{bmatrix} 0\\ 1 \end{bmatrix} [01]变成 [ − 1 0 ] \begin{bmatrix} -1\\ 0 \end{bmatrix} [−10],所以该变换矩阵为: [ 0 − 1 1 0 ] \begin{bmatrix} 0 & -1\\ 1 & 0 \end{bmatrix} [01−10]。
到此,就已经证明了我们在开头所说的:矩阵是一种线性变换。
相关文章:

线性代数本质系列(一)向量,线性组合,线性相关,矩阵
本系列文章将从下面不同角度解析线性代数的本质,本文是本系列第一篇 向量究竟是什么? 向量的线性组合,基与线性相关 矩阵与线性相关 矩阵乘法与线性变换 三维空间中的线性变换 行列式 逆矩阵,列空间,秩与零空间 克莱姆…...

python语法之注释
注释可用于解释Python代码。 注释可用于使代码更易读。 注释可用于在测试代码时阻止执行。 (1)创建注释 注释以#开头,Python会忽略它们: #This is a comment print("Hello, World!") 注释可以放在一行…...

React【异步逻辑createAsyncThunk(一)、createAsyncThunk(二)、性能优化、createSelector】(十二)
文章目录 异步逻辑 createAsyncThunk(一) createAsyncThunk(二) 性能优化 createSelector 异步逻辑 //Product.js const onAdd () > {const name nameRef.current.value// 触发添加商品的事件dispatch(addProduct({name…...
Halcon WPF 开发学习笔记(3):WPF+Halcon初步开发
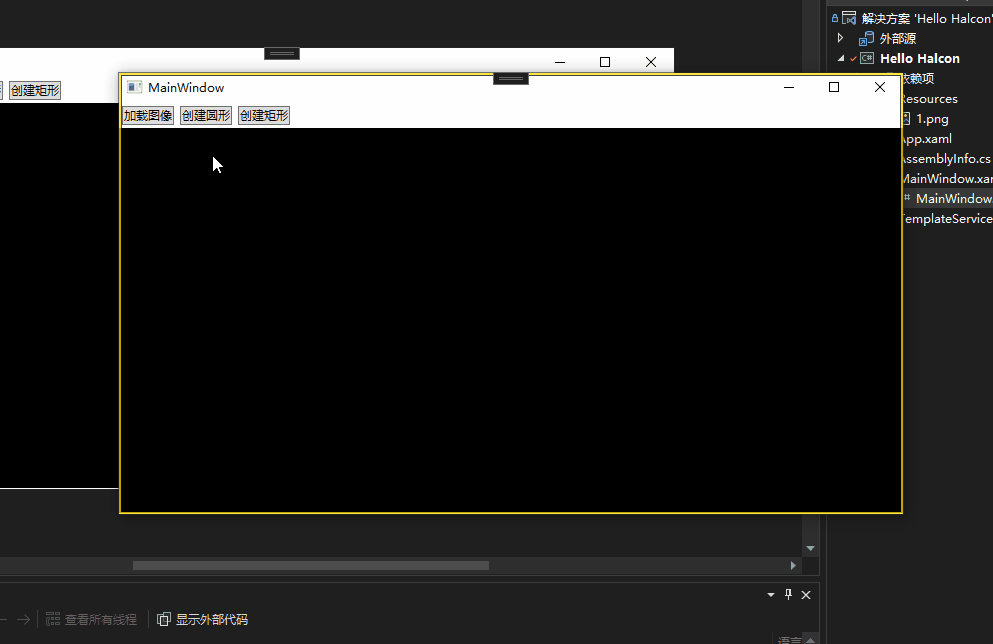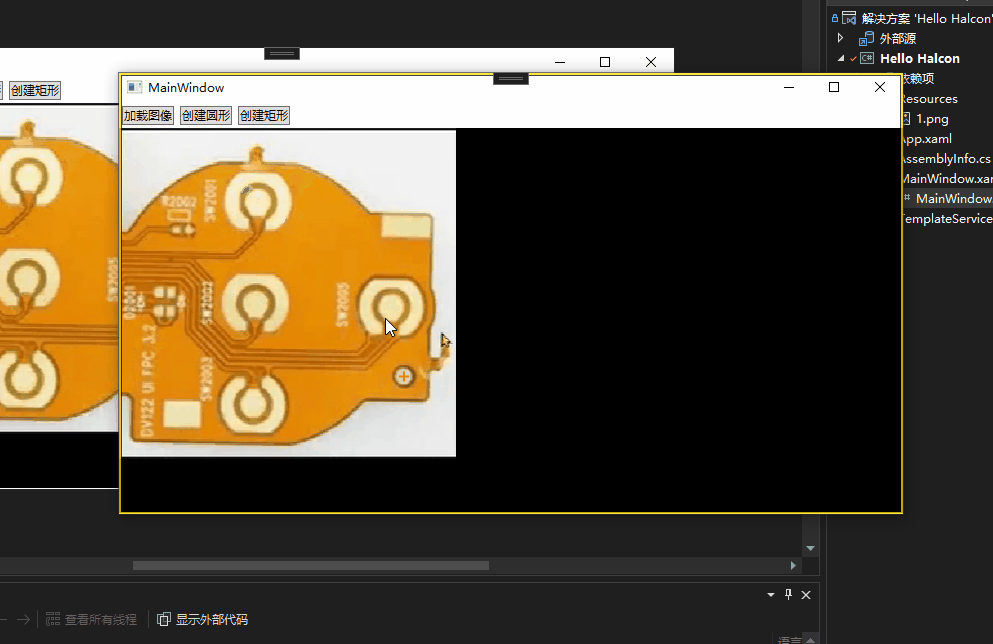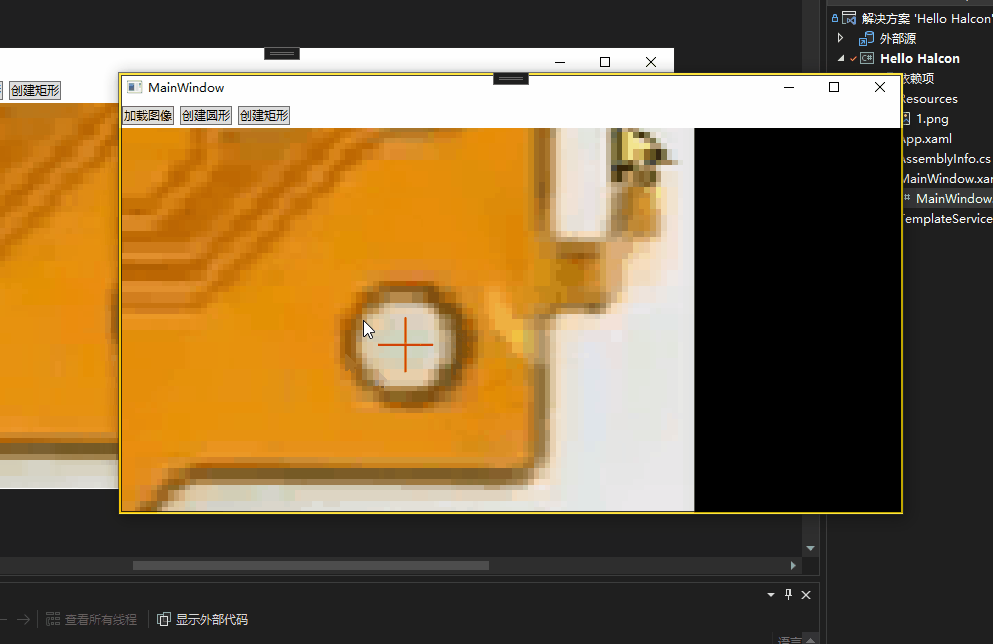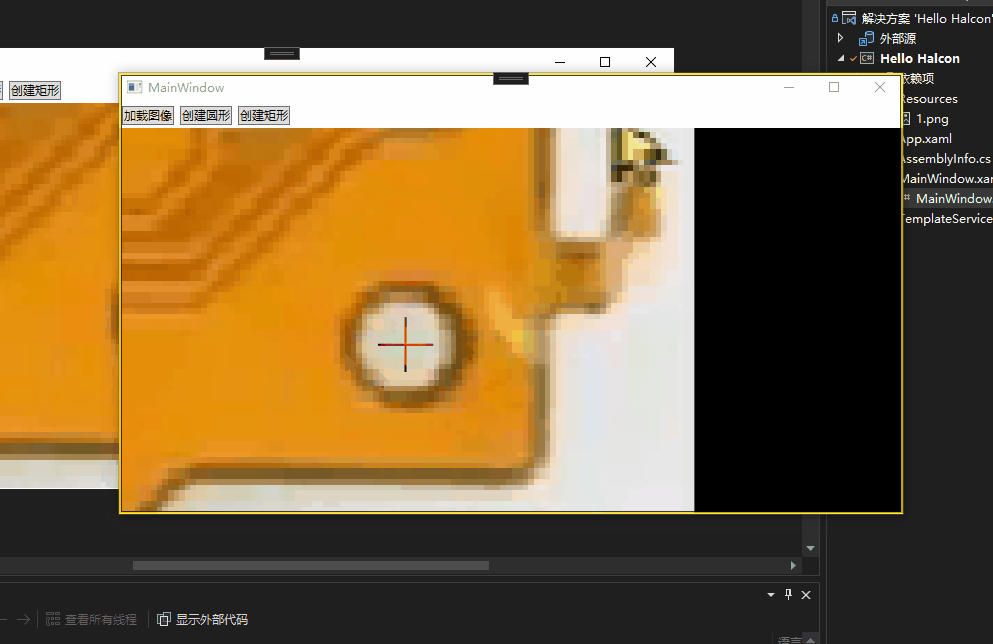
文章目录 前言在MainWindow.xaml里面导入Halcon命名空间WPF简单调用Halcon创建矩形简单调用导出脚本函数 正确显示匹配效果 前言 本章会简单讲解如何调用Halcon组件和接口,因为我们是进行混合开发模式。即核心脚本在平台调试,辅助脚本C#直接调用。 在M…...

P6入门:项目初始化9-项目详情之资源 Resource
前言 使用项目详细信息查看和编辑有关所选项目的详细信息,在项目创建完成后,初始化项目是一项非常重要的工作,涉及需要设置的内容包括项目名,ID,责任人,日历,预算,资金,分类码等等&…...

Python高级语法----使用Python进行模式匹配与元组解包
文章目录 1. 模式匹配的新特性2. 高级元组解包技巧3. 数据类的匹配与应用1. 模式匹配的新特性 Python自3.10版本起引入了结构化模式匹配的新特性,这是一种强大的工具,允许开发者用更清晰、更直观的方式处理数据结构。模式匹配类似于其他编程语言中的switch-case语句,但它更…...
)
MySQL安装配置与使用教程(2023.11.13 MySQL8.0.35)
CONTENTS 1. MySQL的安装与配置2. MySQL常用操作教程 1. MySQL的安装与配置 MySQL Windows Installer 下载地址:MySQL Installer。 我们下载最新版本(目前是8.0.35)的安装包,注意要选择更大的那个,名字为 mysql-inst…...

【阿里云数据采集】采集标准Docker容器日志:部署阿里云Logtail容器以及创建Logtail配置,用于采集标准Docker容器日志
文章目录 引言I 预备知识1.1 Logtail1.2 安装Logtail1.3 创建用户自定义标识机器组1.4 设置logtail容器组件重启策略II 采集服务器日志2.1 采集同一账号下同地域服务器的日志2.2 不同账号下同地域服务器的日志2.3 创建Logtail配置III 查询语法3.1 具体查询语法3.2 查询示例3.3 …...
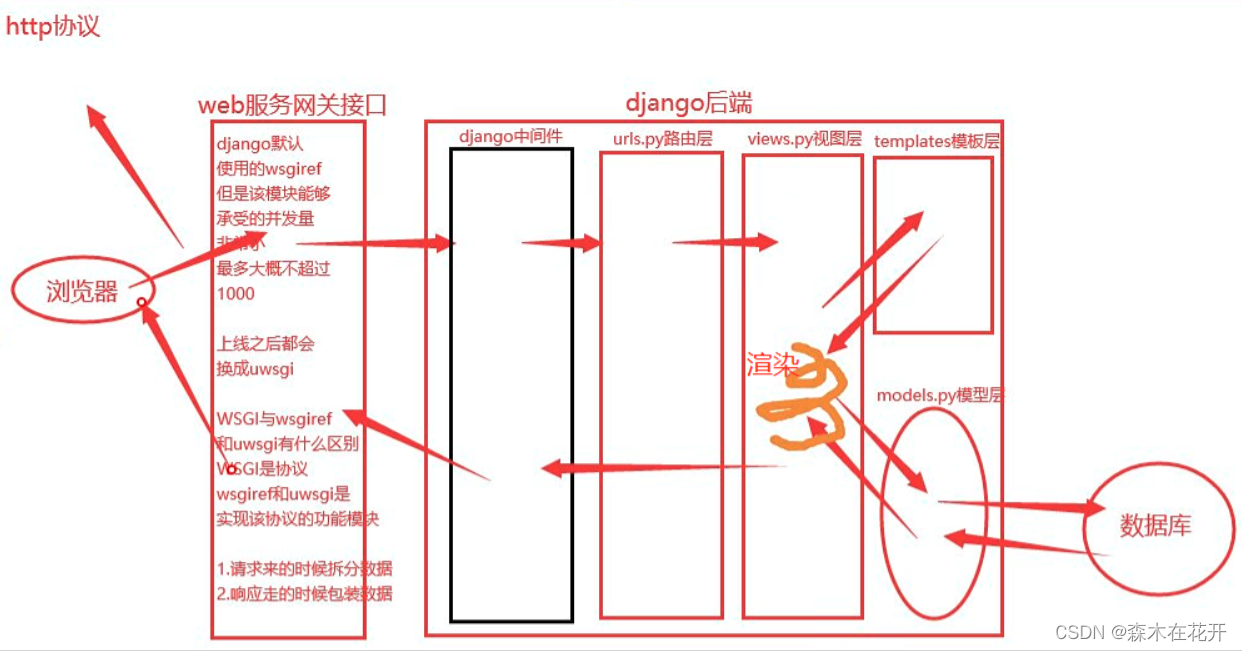
Django中如何创建表关系,请求生命周期流程图
Django中ORM创建表关系 如何创建表关系(一对一 , 一对多 , 多对多) 图书表,出版社表,作者表,作者详情表 换位思考法判断表关系 图书表和出版社表 >>> 一对多 >>> 图书表是多,出…...

MongoDB副本集配置和创建
副本集有三类角色:master(primary),slave(secondary),仲裁服务器。 primary是主,只有primary能写入,secondary无法插入数据,且需要声明是slave才能查看数据 一般生产搞三个服务器做一个master和两个slave&a…...

使用 `open-uri.with_proxy` 方法打开网页
Ruby 爬虫程序如下: require open-uri require nokogiri# 定义代理信息 proxy_host jshk.com.cn# 定义要爬取的网页 URL url http://www.example.com# 使用代理信息打开网页 open-uri.with_proxy(proxy_host, proxy_port) do |proxy|# 使用 Nokogiri 库解析网页内…...

数据库表的设计——范式
目录 1. 设计数据表需要注意的点 2. 范式 2.1 范式简介 2.2 范式有哪些? 2.3 第一范式(1NF) 2.4 第二范式(2NF) 2.5 第三范式(3NF) 2.6 小结 1. 设计数据表需要注意的点 (1)首先要考虑设计这张表的用途,这张表都要存放什…...
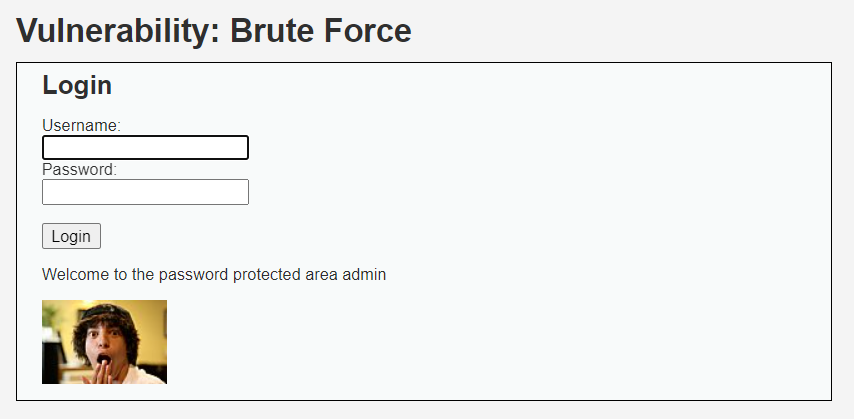
Brute Force
Brute Force "Brute Force"(暴力破解)指的是一种通过尝试所有可能的组合来获取访问、解密或破解信息的攻击方法。这种攻击方法通常是基于暴力和不断尝试的,不依赖漏洞或弱点。通常用于破解密码、破坏系统或获取未经授权的访问权限…...

HTML简单介绍
且视他人之疑目如盏盏鬼火,大胆地去你的夜路。 目录 1.网页 2.Web标准 3.HTML 3.1HTML结构 3.2HTML标签编辑 4.标签介绍 4.1排版标签 4.2文本格式化标签 4.3媒体标签 4.3.1图片标签 4.3.2 音频标签 4.3.3视频标签 5.相对路径 6.链接标签 6.1target属…...

【Java笔试强训】Day10(CM62 井字棋、HJ87 密码强度等级)
CM62 井字棋 链接:井字棋 题目: 给定一个二维数组board,代表棋盘,其中元素为1的代表是当前玩家的棋子,0表示没有棋子,-1代表是对方玩家的棋子。当一方棋子在横竖斜方向上有连成排的及获胜(及…...

C语言求数组中出现次数最多的元素
一、前言 遇到一个需求,需要求数组中出现次数最多的元素,查找了一些资料,结合自己的思路,编写了程序并验证。 只考虑元素为非负整数的数组,如果有出现次数相同的元素,则返回较小元素。 二、编程思路 以数…...

【Python Opencv】Opencv画图形
文章目录 前言一、画图形1.1 画线1.2 画矩形1.3 画圆1.4 画椭圆1.5 添加文本 总结 前言 在计算机视觉和图像处理中,OpenCV不仅可以处理图像和视频,还提供了一组功能强大的工具,用于在图像上绘制各种形状和图形。这些功能使得我们能够在图像上…...

了解防抖和节流:提升前端交互体验的实用策略
了解防抖和节流:提升前端交互体验的实用策略 前言什么是防抖?什么是节流?应用实例防抖实例节流实例 前言 本文将重点介绍前端性能优化方法之一的防抖和节流。首先解释了它们的概念和原理,然后探讨了它们在前端开发中的应用场景&a…...

SQL学习之增删改查
文章目录 数据库数据类型建表create table插入数据insert into查询数据select from修改数据update set删除数据delete from备份ctas结果插入iis截断表 truncate table修改表结构alter table添加注释 注:本文的SQL语法是基于Oracle数据库操作的,但是基本的…...
Ansible角色定制实例
目录 角色定制:roles 角色定制实例:利用角色部署wordpress 1.在roles目录下生成对应的目录结构 2.定义配置文件 ①nginx ②php ③mysql ④定义剧本文件 ⑤启动服务 角色定制:roles 对于普通的剧本(playbook)有…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...

初探用uniapp写微信小程序遇到的问题及解决(vue3+ts)
零、关于开发思路 (一)拿到工作任务,先理清楚需求 1.逻辑部分 不放过原型里说的每一句话,有疑惑的部分该问产品/测试/之前的开发就问 2.页面部分(含国际化) 整体看过需要开发页面的原型后,分类一下哪些组件/样式可以复用,直接提取出来使用 (时间充分的前提下,不…...
