激活函数的本质
激活函数(Activation Function)
是神经网络中的一种函数,它接受一个输入(通常是神经元的加权和)并产生一个输出作为神经元的最终输出。激活函数的作用是引入非线性性,使神经网络能够学习复杂的模式和关系。
在神经网络中,激活函数通常被用于每个神经元的输出,以便引入非线性变换。如果没有激活函数,整个神经网络将由线性变换组成,多个线性变换的组合仍然是线性的。通过引入非线性激活函数,神经网络可以学习和表示更复杂的函数关系,使其能够适应更广泛的问题。
常见的激活函数包括:
-
Sigmoid 函数(Logistic 函数): 将输入映射到范围 (0, 1) 之间,常用于输出层的二分类问题。
[ \text{sigmoid}(x) = \frac{1}{1 + e^{-x}} ]
-
Tanh 函数: 类似于 Sigmoid 函数,但将输入映射到范围 (-1, 1) 之间,有时在隐藏层中使用。
[ \text{tanh}(x) = \frac{e^{x} - e{-x}}{e{x} + e^{-x}} ]
-
ReLU 函数(Rectified Linear Unit): 将负数映射为零,对正数保持不变。是目前最常用的激活函数之一。
[ \text{ReLU}(x) = \max(0, x) ]
-
Leaky ReLU 函数: 与 ReLU 类似,但对负数的输出有一个小的斜率,避免了 ReLU 的一些问题。
[ \text{Leaky ReLU}(x) = \max(\alpha x, x) ],其中 (\alpha) 是一个小的正数。
-
Softmax 函数: 用于多分类问题的输出层,将输入转化为概率分布。
[ \text{Softmax}(x_i) = \frac{e{x_i}}{\sum_{j=1}{K}e^{x_j}} ],其中 (K) 是类别的数量。
不同的激活函数适用于不同类型的问题和网络结构,选择合适的激活函数对神经网络的性能和训练过程都有影响。
非线性变换
非线性变换是指输入与输出之间的关系不是线性的。在数学上,如果一个变换是线性的,它应该满足两个性质:可加性和齐次性。可加性意味着变换对两个输入的和等于两个输入分别经过变换后的和,而齐次性意味着变换对输入的缩放等于输入经过变换后的缩放。如果一个变换不满足这两个性质,那么它就是非线性的。
在神经网络中,非线性变换是通过激活函数引入的。神经元的输出经过激活函数后才成为网络的最终输出。如果没有激活函数,多层神经网络的组合将简化为单一的线性变换,因为线性函数的组合仍然是线性的。引入非线性激活函数后,神经网络能够学习和表示更加复杂的关系和模式,因为非线性函数能够捕捉数据中的非线性结构。
举例来说,假设有一个简单的神经网络层,每个神经元的输出 (y) 是输入 (x) 的线性组合和激活函数 (f) 的结果:
[ y = f(Wx + b) ]
其中,(W) 是权重矩阵,(b) 是偏置,(f) 是激活函数。如果 (f) 是一个线性函数,那么整个变换仍然是线性的。但如果 (f) 是一个非线性函数,比如 ReLU,tanh 或 sigmoid,那么整个变换就是非线性的。
引入非线性变换是为了增强神经网络的表达能力,使其能够学习和适应更为复杂的模式和关系,从而提高网络在处理各种任务上的性能。
让我们通过简单的例子来说明线性和非线性的概念。
-
线性关系:
假设有一个简单的线性关系,例如 (y = 2x + 3)。这是一个线性函数,因为 (y) 和 (x) 之间的关系是直线,且满足线性方程。
| (x) | (y) |
|---|---|
| 1 | 5 |
| 2 | 7 |
| 3 | 9 |
在这个例子中,当 (x) 增加1时,(y) 增加2,符合线性关系。
-
非线性关系:
现在考虑一个非线性关系,例如 (y = x^2)。这是一个非线性函数,因为 (y) 和 (x) 之间的关系是二次曲线,不满足线性方程
| (x) | (y) |
| ----- | ----- |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |在这个例子中,当 (x) 增加1时,(y) 不仅增加1,而是增加了原来的 (x) 的平方。
总的来说,线性关系是指两个变量之间的关系是一条直线,而非线性关系则是指关系不是直线的。在神经网络中,引入非线性变换是为了使网络能够学习和表示更为复杂的模式和关系,因为许多现实世界的问题和数据都包含非线性结构。希望这个例子能帮助你更好地理解线性和非线性的概念。
非线性的好处
就是让线/面更容易拟合点
引入非线性变换的好处在于增强神经网络的表达能力,使其能够学习和适应更为复杂的模式和关系。以下是一些非线性变换的好处:
-
学习非线性关系: 现实世界中的许多问题和数据包含复杂的非线性结构。通过使用非线性激活函数,神经网络能够更灵活地拟合和学习这些非线性关系,从而提高模型的性能。
-
表示层次特征: 非线性激活函数允许神经网络在不同层次上学习抽象和高级的特征。多层非线性变换可以逐渐构建复杂的特征表示,从而更好地捕捉数据的结构和模式。
-
解决分类问题: 对于分类问题,非线性变换可以使神经网络学习非线性决策边界,从而更好地区分不同类别。这对于处理复杂的分类任务非常重要。
-
防止信息损失: 在深度神经网络中,经过多次线性变换后,输出仍然是输入的线性组合。这样可能导致信息的丢失,因为多次线性变换等效于一次线性变换。通过引入非线性激活函数,可以防止信息在网络中的线性传递,从而保留更多的信息。
-
梯度下降的非线性优化: 非线性激活函数引入了非线性性质,这对优化算法(如梯度下降)的收敛至关重要。线性函数的组合仍然是线性的,容易导致梯度消失或爆炸的问题,而非线性激活函数有助于缓解这些问题。
总的来说,非线性变换使神经网络更具灵活性,能够处理更为复杂的任务和数据。这是深度学习成功的一个关键因素,因为它使神经网络能够适应各种不同的模式和结构,提高了模型的泛化能力。
相关文章:

激活函数的本质
激活函数(Activation Function) 是神经网络中的一种函数,它接受一个输入(通常是神经元的加权和)并产生一个输出作为神经元的最终输出。激活函数的作用是引入非线性性,使神经网络能够学习复杂的模式和关系。…...
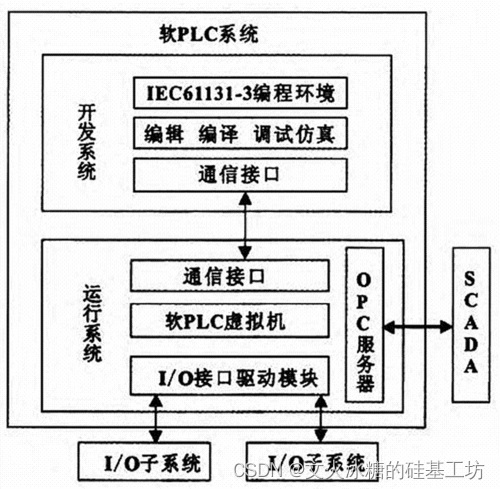
[工业自动化-18]:西门子S7-15xxx编程 - 软件编程 - PLC用于工业领域的嵌入式系统:硬件原理图、指令系统、系统软件架构、开发架构等
目录 前言: 一、PLC的硬件电路原理 1.1 硬件框图 1.2 硬件模块详解 (1)CPU (2)存储器 (3)输入/输出(I/O)模块 (4)编程器 (5&a…...

【C++】——运算符重载
🎃个人专栏: 🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客 🐳Java基础:Java基础_IT闫的博客-CSDN博客 🐋c语言:c语言_IT闫的博客-CSDN博客 🐟MySQL:…...

怎么理解独立机器和虚拟机
独立服务器:顾名思义,就是一个放在机房的实实在在的物理服务器,一个单独的主机(具有性能高,处理速度快等优点,但 也有价格高,可扩展性不强等缺点) vps:虚拟专用服务器,一…...
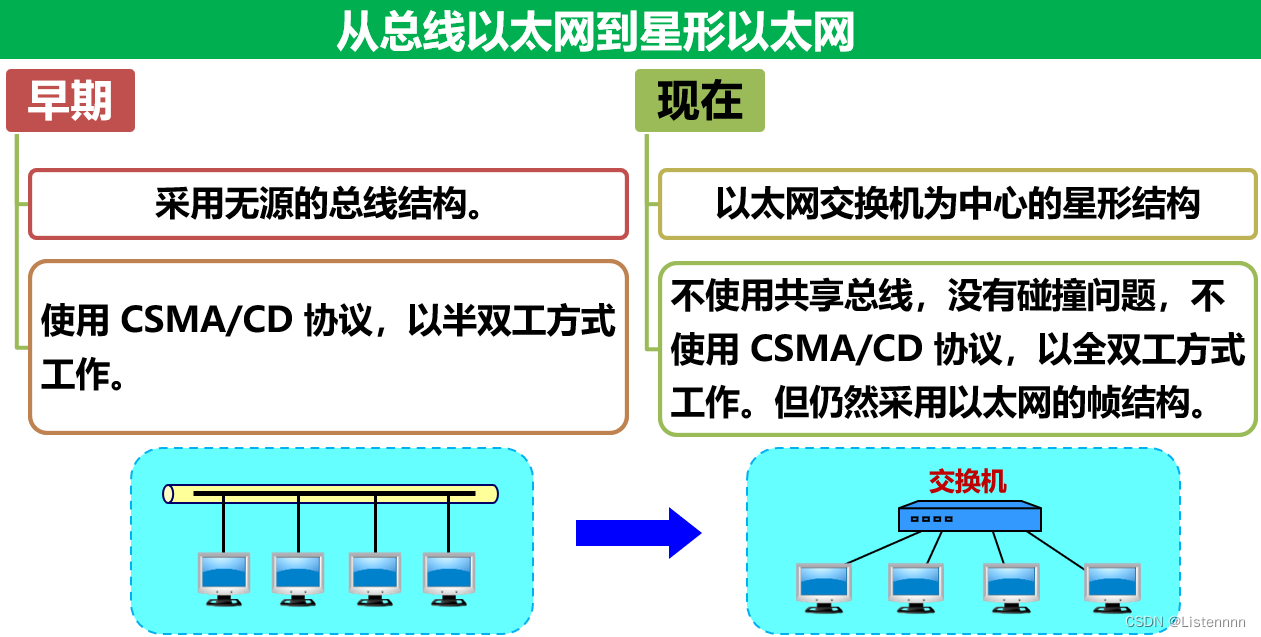
以太网和局域网
计算机网络的定义 计算机网络是一个将分散的、具有独立功能的计算机,通过通信设备与线路连接起来,由根据协议编写的软件来实现的资源共享和信息传递的系统 计算机网络的分类 广域网是互联网的核心部分 局域网 常见的局域网拓扑结构有4大类:…...
)
【Git】第三篇:基本操作(配置本地仓库)
初次使用git需要设置你的用户名以及邮箱,这将作为当前机器git的标识,如果你用它来下载远程仓库一些需要登录权限的仓库会要求登录,git默认使用配置邮箱以及用户名登入,但会要求你手动输入密码。 配置本地仓库:git con…...

JS中sort排序
在我们JS排序中,有许多排序的方法,比如冒泡排序、选择排序等等。这次我为大家介绍一下sort排序! sort 按照 Unicode code 位置排序,默认升序 默认情况下,sort()会按照升序重新排序数组,即最小值在前最大值…...
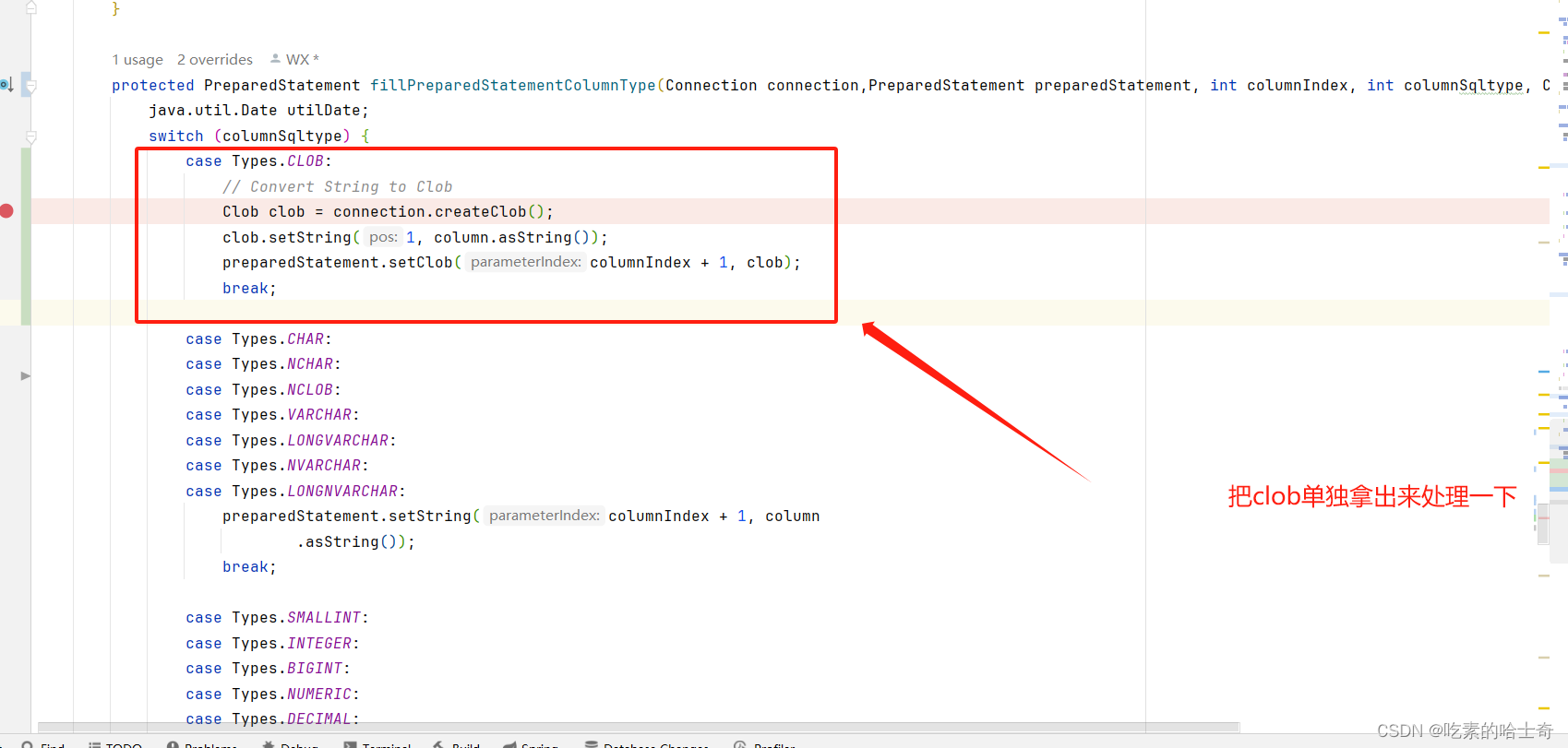
【现场问题】datax中write部分为Oracle的时候插入clolb类型字段,插入的数据为string且长度过场问题
datax的Oraclewriter 报错显示查询报错展示查找datax中的数据插入模块 报错显示 occurred during batching: ORA-01704: string literal too long 查询报错展示 基本上查到的都是这样的,所以锁定是clob的字段类型的问题,而且是只有Oracle出问题&#…...
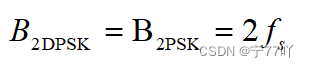
ASK、PSK、FSK的调制与解调
ASK、PSK、FSK的调制与解调 本文主要涉及数字信号的调制与解调,内容包括:2ASK、2PSK、2FSK的调制与解调以及频谱分析 关于通信原理还有其他文章可参考: 1、信息量、码元、比特、码元速率、信息速率详细解析——实例分析 2、模拟系统的AM信号的…...
基于XML的声明式事务
场景模拟 参考基于注解的声明式事务 修改Spring的配置文件 将Spring配置文件中去掉tx:annotation-driven标签,并添加配置: <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.springframework.org…...

力扣labuladong一刷day9滑动窗口共4题
力扣labuladong一刷day9滑动窗口共4题 文章目录 力扣labuladong一刷day9滑动窗口共4题一、76. 最小覆盖子串二、567. 字符串的排列三、438. 找到字符串中所有字母异位词四、3. 无重复字符的最长子串 一、76. 最小覆盖子串 题目链接:https://leetcode.cn/problems/m…...
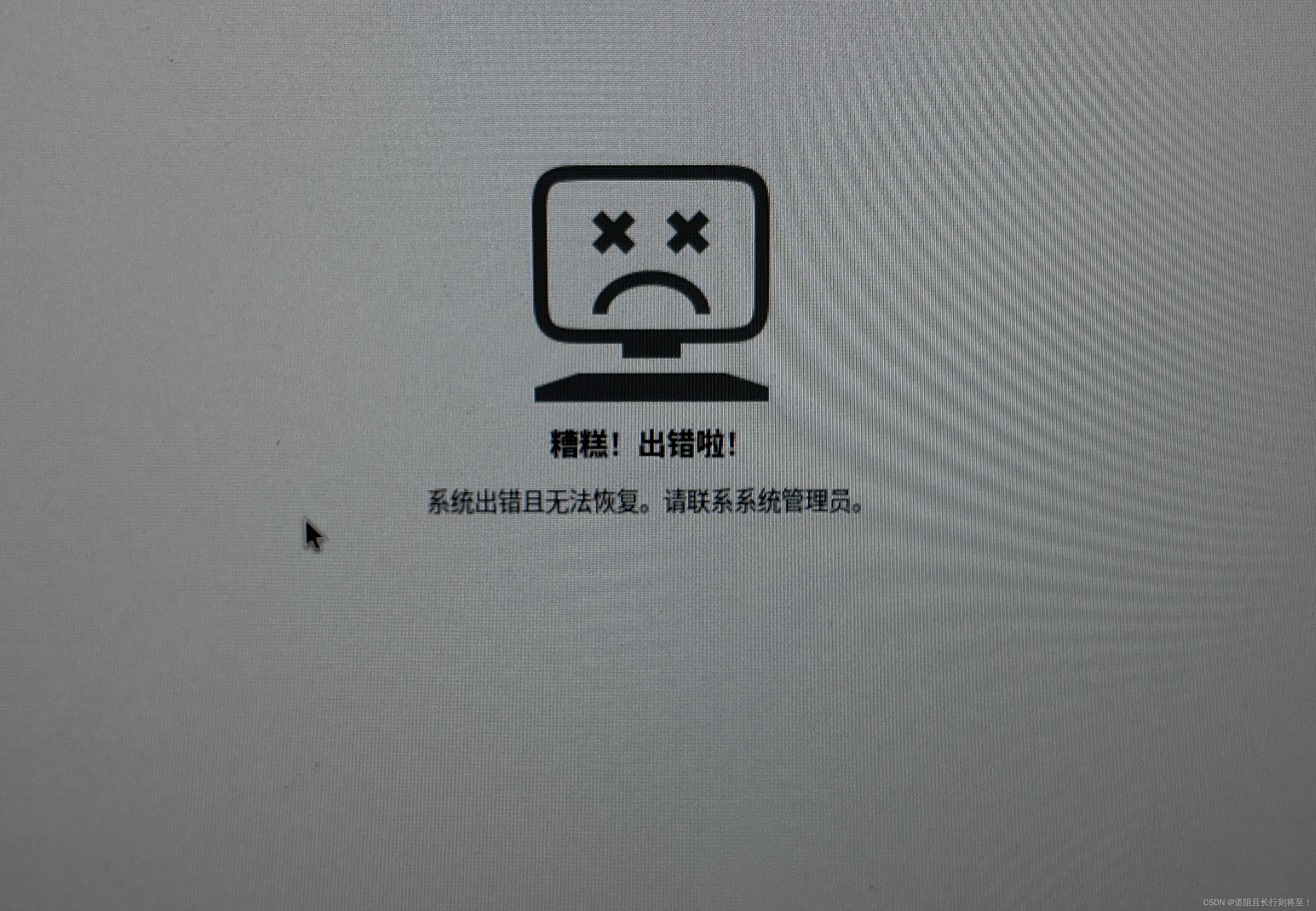
ubuntu开机系统出错且无法恢复。请联系系统管理员。
背景: ubuntu22.04.2命令行,执行自动安装系统推荐显卡驱动命令,字体变大,重启后出现如下图错误,无法进入系统,无法通过CTRLALTF1-F3进入TTY模式。 解决办法: 1.首先要想办法进入系统ÿ…...
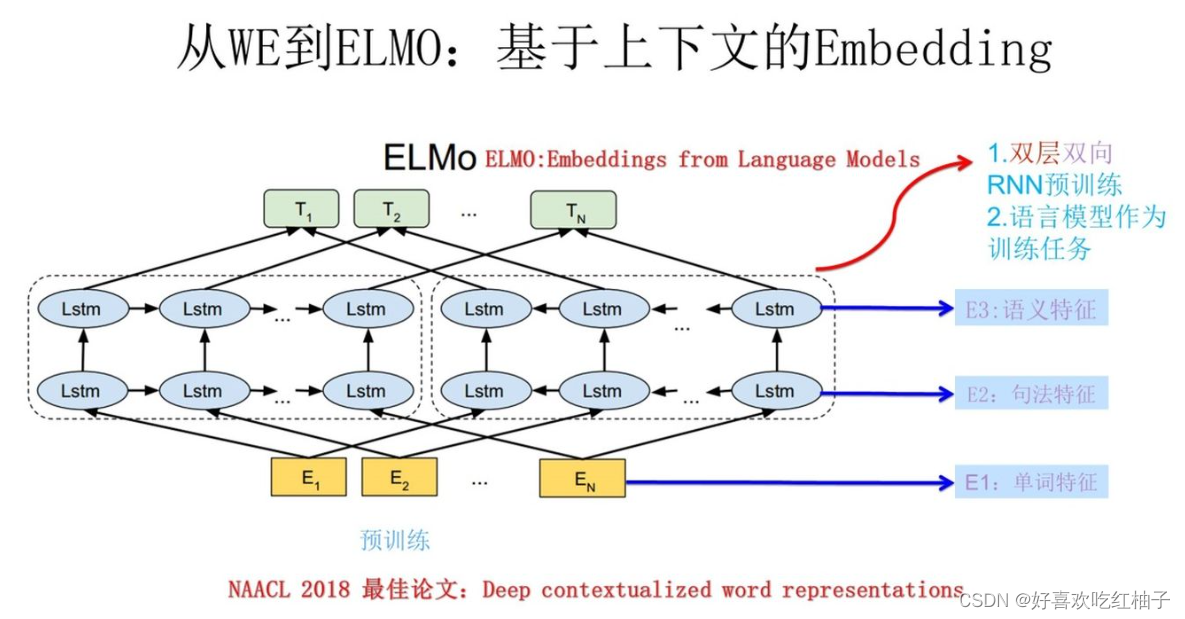
Transformer详解一:transformer的由来和先导知识
目录 参考资料前言一、预训练二、神经网络语言模型(NNLM):预测下一个词one-hot编码的缺陷词向量(word embedding) 三、Word2Vec模型:得到词向量CBOWSkip-gramWord2Vec和NNLM的区别Word2Vec的缺陷 四、ELMO模…...

数字化产品经理的金字塔能力模型
在企业数字化转型的浪潮下,要求IT团队更加主动的服务业务、赋能业务,而数字化产品经理正是IT、业务融合的桥梁,该岗位需要具备业务、技术、商业的复合知识结构,并且拥有很强的自驱力。那么数字化产品经理在企业如何产生价值、赋能…...

这 11 个 for 循环优化你得会
日常开发中,经常会遇到一些循环耗时计算的操作,一般也都会采用 for 循环来处理,for 作为编程入门基础,主要是处理重复的计算操作,虽然简单好用,但在写法上也有很多的考究,如果处理不好ÿ…...

JVM字符串常量池StringTable
目录 一、StringTable为什么要调整 二、String的基本特性 三、String的内存分配 四、字符串拼接操作 五、intern()方法 六、Stringtable的垃圾回收 七、G1中String去重操作 一、StringTable为什么要调整 jdk7之前,hotspot对于方法区的实现是永久代ÿ…...

【华为OD题库-010】寻找矿堆的最大价值-Java
题目 给你一个由0(空地)、1(银矿)、2(金矿)组成的的地图,矿堆只能由上下左右相邻的金矿或银矿连接形成。超出地图范围可以认为是空地。 假设银矿价值1,金矿价值2,请你找出地图中最大价值的矿堆并输出该矿堆的价值 输入描述 地图元素信息如: 2…...
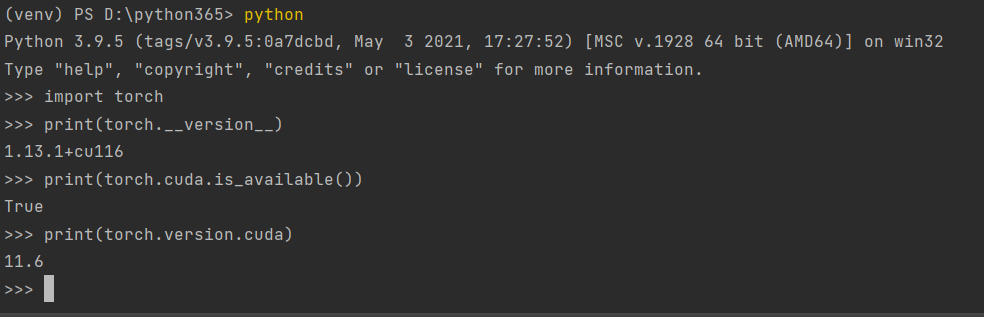
在PyTorch中使用CUDA, pytorch与cuda不同版本对应安装指南,查看CUDA版本,安装对应版本pytorch
目录 1 查看本机CUDA版本 2 查看对应CUDA的对应pytorch版本安装 3 用pip 安装 4 用conda安装 5 验证安装 在PyTorch中使用CUDA,根据你的具体环境和需求调整版本号,确保安装的PyTorch版本与你的CUDA版本兼容。 在PyTorch中使用CUDA,你需…...
copilot 产生 python工具函数并生成单元测试
stock.py 这个文件,我只写了注释(的开头),大部分注释内容和函数都是copilot # split a string and extract the environment variable from it # input can be , pathabc, pathabc;pathdef, pathabc;pathdef;pathghi # output i…...
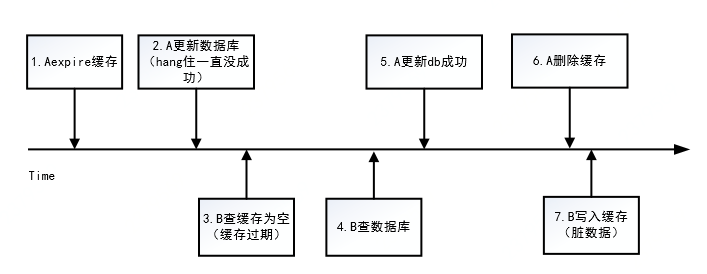
缓存与数据库双写一致性几种策略分析
一、背景 在高并发场景中,为防止大量请求直接访问数据库,缓解数据库压力,常用的方式一般会增加缓存层起到缓冲作用,减少数据库压力。引入缓存,就会涉及到缓存与数据库中数据如何保持一致性问题,本文将对几…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
