acwing算法基础之数学知识--求数a的欧拉函数值phi(a)
目录
- 1 基础知识
- 2 模板
- 3 工程化
1 基础知识
数a的欧拉函数 ϕ ( a ) \phi(a) ϕ(a):表示1~n中与n互质的数的个数。其中两个数互质,是指这两个数的最大公约数为1。
根据定义,我们可以写出如下方法,
int gcd(int a, int b) {return b ? gcd(b, a % b) : a;
}int phi(int a) {int res = 0;for (int i = 1; i <= a; ++i) {if (gcd(i, a) == 1) {res += 1;}}return res;
}
但存在更快的求解方法,见如下关键步骤:
- 对数a进行分解质因子操作。
a = p 1 α 1 ⋅ p 2 α 2 ⋯ p k α k a=p_1^{\alpha_1} \cdot p_2^{\alpha_2}\cdots p_k^{\alpha_k} a=p1α1⋅p2α2⋯pkαk
unordered_map<int,int> get_prime_divisors(int a) {unordered_map<int,int> mp;for (int i = 2; i <= a / i; ++i) {if (a % i == 0) {int s = 0;while (a % i == 0) {a /= i;s++;}mp[i] = s;}}if (a > 1) mp[a] = 1;return mp;
}
- 计算数a的欧拉函数,
ϕ ( a ) = a ⋅ ( 1 − 1 p 1 ) ⋅ ( 1 − 1 p 2 ) ⋯ ( 1 − 1 p k ) \phi(a)=a\cdot (1-\frac{1}{p_1}) \cdot (1-\frac{1}{p_2}) \cdots (1-\frac{1}{p_k}) ϕ(a)=a⋅(1−p11)⋅(1−p21)⋯(1−pk1)
int phi(int a, unordered_map<int,int> mp) {int res = a;for (auto [x, y] : mp) {res = res / x * (x - 1);}return res;
}
可以将以上两步合并,请看如下代码,
int phi(int a) {int res = a;for (int i = 2; i <= a / i; ++i) {if (a % i == 0) {res = res / i * (i - 1);while (a % i == 0) {a /= i;}}}if (a > 1) {res = res / a * (a - 1);}return res;
}
2 模板
int phi(int x)
{int res = x;for (int i = 2; i <= x / i; i ++ )if (x % i == 0){res = res / i * (i - 1);while (x % i == 0) x /= i;}if (x > 1) res = res / x * (x - 1);return res;
}
3 工程化
题目1:输入n个数,请分别求出它们的欧拉函数值。
#include <iostream>using namespace std;int main() {int n;cin >> n;while (n--) {int x;cin >> x;int res = x;for (int i = 2; i <= x / i; ++i) {if (x % i == 0) {res = res / i * (i - 1);while (x % i == 0) x /= i;}}if (x > 1) res = res / x * (x - 1);cout << res << endl;}return 0;
}
相关文章:
)
acwing算法基础之数学知识--求数a的欧拉函数值phi(a)
目录 1 基础知识2 模板3 工程化 1 基础知识 数a的欧拉函数 ϕ ( a ) \phi(a) ϕ(a):表示1~n中与n互质的数的个数。其中两个数互质,是指这两个数的最大公约数为1。 根据定义,我们可以写出如下方法, int gcd(int a, int b) {retu…...
Jenkins的介绍与相关配置
Jenkins的介绍与配置 一.CI/CD介绍 1.CI/CD概念 ①CI 中文意思是持续集成 (Continuous Integration, CI) 是一种软件开发流程,核心思想是在代码库中的每个提交都通过自动化的构建和测试流程进行验证。这种方法可以帮助团队更加频繁地交付软件&#x…...

开源网安受邀参加网络空间安全合作与发展论坛,为软件开发安全建设献计献策
11月10日,在广西南宁举办的“2023网络空间安全合作与发展论坛”圆满结束。论坛在中国兵工学会的指导下,以“凝聚网络空间安全学术智慧,赋能数字经济时代四链融合”为主题,邀请了多位专家及企业代表共探讨网络安全发展与数字经济…...
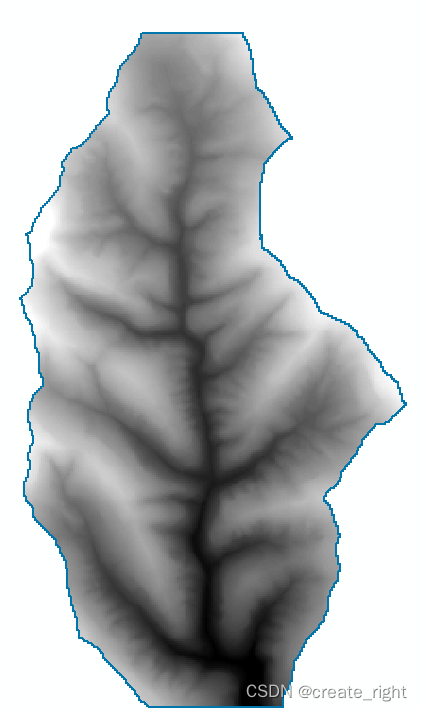
arcgis提取栅格有效边界
方法一:【3D Analyst工具】-【转换】-【由栅格转出】-【栅格范围】 打开一幅栅格数据,利用【栅格范围】工具提取其有效边界(不包含NoData值): 方法二:先利用【栅格计算器】将有效值赋值为1,得到…...

后端接口性能优化分析-问题发现问题定义
👏作者简介:大家好,我是爱吃芝士的土豆倪,24届校招生Java选手,很高兴认识大家📕系列专栏:Spring源码、JUC源码🔥如果感觉博主的文章还不错的话,请👍三连支持&…...

中国首个通过ASIL D认证的IP发布,国产芯片供应商的机会来了
来自智能汽车的“芯”安全需求正在快速爆发。 一方面,随着智能汽车ADAS的快速迭代与逐渐普及化,以及越来越多元化智能座舱功能的快速上车,由此带来的车辆信息安全场景也在与日俱增,例如云端链接、设备身份认证、自动驾驶安全保障…...
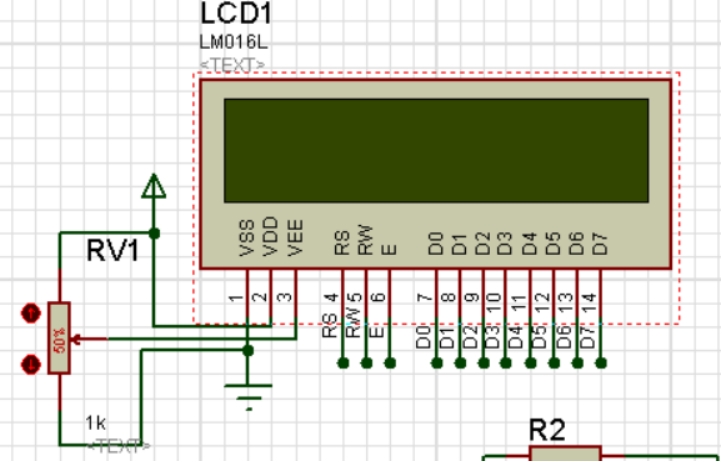
[单片机课程设计报告汇总] 单片机设计报告常用硬件元器件描述
[单片机课程设计必看] 单片机设计报告常用描述 硬件设计 AT89C51最小系统 AT89C51是美国ATMEL公司生产的低电压,高性能CMOS16位单片机,片内含4k bytes的可反复擦写的只读程序存储器和128 bytes的随机存取数据存储器,期间采用ATMEL公司的高…...
Docker学习——⑧
文章目录 1、什么是 Docker Compose(容器编排)2、为什么要 Docker Compose?3、Docker Compose 的安装4、Docker Compose 的功能和使用场景5、Docker Compose 文件(docker-compose.yml)5.1 文件语法版本5.2 文件基本结构及常见指令 6、Docker …...

力扣刷题第二十一天--栈与队列
前言 周末玩了两天,s赛看的难受。。。还是和生活对线吧 内容 一、用栈实现队列 232.用栈实现队列 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类&#…...
Python基础-解释器安装
一、下载 网址Welcome to Python.orgPython更新到13了,我们安装上一个12版本。 这里我保存到网盘里了,不想从官网下的,可以直接从网盘里下载。 链接:百度网盘 请输入提取码百度网盘为您提供文件的网络备份、同步和分享服务。空间…...
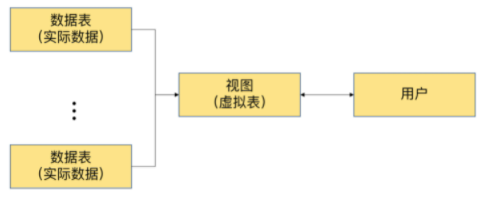
MySQL(14):视图
数据库对象 对象描述表(TABLE)表是存储数据的逻辑单元,以行和列的形式存在,列就是字段,行就是记录数据字典就是系统表,存放数据库相关信息的表。系统表的数据通常由数据库系统维护,程序员通常不应该修改,只…...
Blazor 附件上传和下载功能
效果图 page "/uploadFile" inject Microsoft.AspNetCore.Hosting.IWebHostEnvironment WebHostEnvironment inject ToastService ToastService inject DownloadService DownloadService<h3>UploadFile</h3><Button OnClick"ButtonClick" C…...
Git 安装配置
目录 Linux 平台上安装 Debian/Ubuntu Centos/RedHat 源码安装 Windows 平台上安装 Mac 平台上安装 Git 配置 用户信息 文本编辑器 差异分析工具 查看配置信息 在使用Git前我们需要先安装 Git。Git 目前支持 Linux/Unix、Solaris、Mac和 Windows 平台上运行。 Git …...
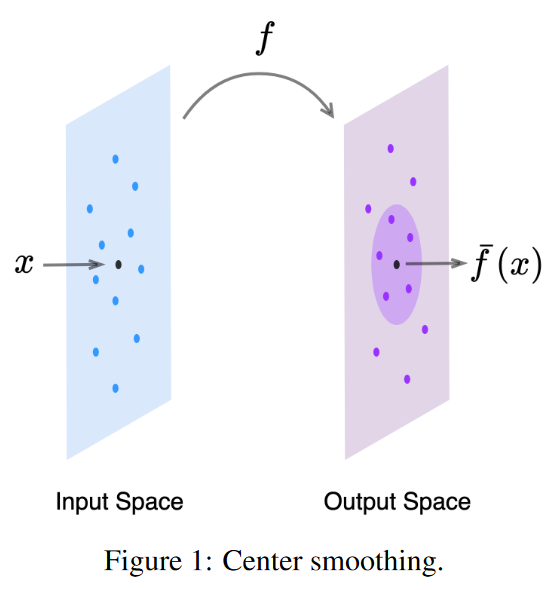
Center Smoothing Certified Robustness for Networks with Structured Outputs
文章目录 Center Smoothing: Certified Robustness for Networks with Structured OutputsSummaryResearch ObjectiveProblem StatementMethodsEvaluationConclusionNotesGaussian Smoothing常用希腊字母霍夫丁不等式(Hoeffdings inequality)1.简述2.霍夫…...

C#几种截取字符串的方法
在C#编程中,经常需要对字符串进行截取操作,即从一个长字符串中获取所需的部分信息。本文将介绍几种常用的C#字符串截取方法,并提供相应的示例代码。 目录 1. 使用Substring方法2. 使用Split方法3. 使用Substring和IndexOf方法4. 使用Regex类…...

【PG】PostgreSQL高可用方案repmgr部署(非常详细)
目录 简介 1 概述 1.1 术语 1.2 组件 1.2.1 repmgr 1.2.2 repmgrd 1.3 Repmgr用户与元数据 2 安装部署 2.0 部署环境 2.1 安装要求 2.1.1 操作系统 2.1.2 PostgreSQL 版本 2.1.3 操作系统用户 2.1.4 安装位置 2.1.5 版本要求 2.2 安装 2.2.1 软件包安装 2.2…...

Linux Makefile配置问题
编写一个简单的工程文件,制作Makefile需要包含lpthread,当Makefile写为如下配置时 #CROSSCOMPILE : arm-linux- CROSSCOMPILE :CFLAGS : -Wall -O2 -c CFLAGS -I$(PWD)LDFLAGS : -lpthread LDFLAGS -lm -ldlCC : $(CROSSCOMPILE)gcc #LD :…...

k8s篇之underlay网络和overlay区别
k8s中underlay网络和overlay区别 一、网络 1 Overlay网络: Overlay叫叠加网络也叫覆盖网络,指的是在物理网络的基础之上迭代实现新的虚拟网络,即可使网络中的容器可以互相通信。 优点是对物理网络的兼容性比较好,可以实现pod的…...

掉瓶子小游戏
欢迎来到程序小院 掉瓶子 玩法:旋转的瓶子,根据瓶子方向,点击鼠标左键瓶子掉落,从桌面中间掉下即得1分,卡在桌边瓶子碎了游戏结束,快去掉瓶子吧^^。开始游戏https://www.ormcc.com/play/gameStart/203 htm…...
Elasticsearch7 入门 进阶
1、全文检索 1.1、数据分类 按数据分类的话,主要可以分为以下三类: 结构化数据:固定格式、有限长度,比如mysql存的数据非结构化数据:不定长、无固定格式,比如邮件、Word文档、日志等半结构化数据…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
