322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins =[1, 2, 5], amount =11输出:3解释:11 = 5 + 5 + 1
示例 2:
输入:coins =[2], amount =3输出:-1
示例 3:
输入:coins = [1], amount = 0 输出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
class Solution {
public:int coinChange(vector<int>& coins, int amount) {//问最少硬币数。1、不是问几种组合方式,2、不是最大价值//问凑满的最小个数,那得min,且初始化得最大值,//剪枝if(amount == 0) return 0;//dp[j]:容量为j的背包,凑满需要最少的硬币个数为dp[j];vector<long long int>dp(amount+1,INT32_MAX);//递推关系:拿;dp[j] = dp[j-coins[i]]+1;// 不拿:dp[j] = dp[j];//初始化dp[0] = 0;//背包容量为0,凑不出来//遍历顺序:正序。求得是个数,跟组合排列无关for(int i = 0;i < coins.size();i++){for(long long int j = coins[i];j <= amount;j++){dp[j] = min(dp[j], dp[j-coins[i]]+1);}}if(dp[amount] == 0 || dp[amount] == INT32_MAX) return -1;return dp[amount];}
};相关文章:

322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬币的数量是无限的。 示…...
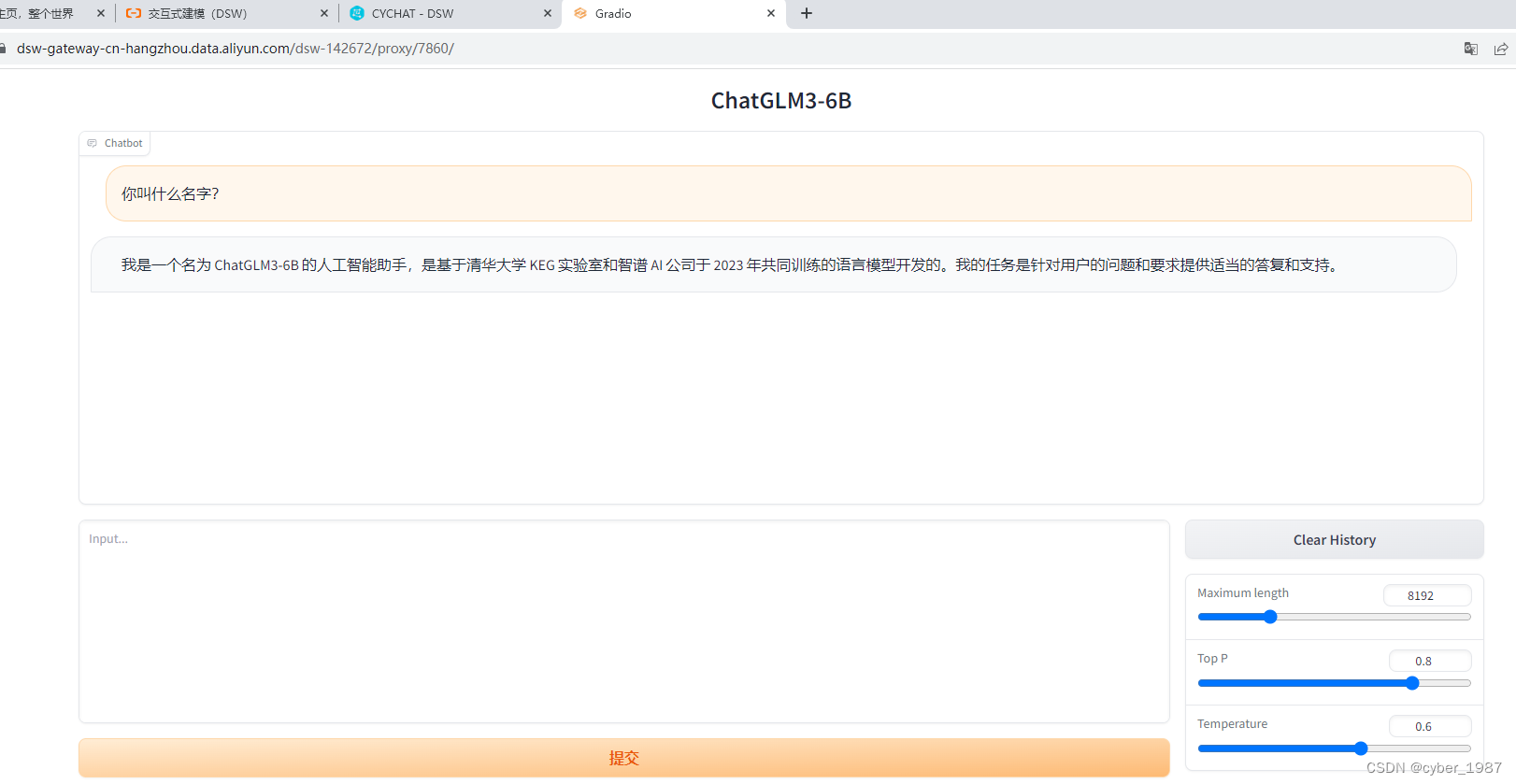
【大模型-第一篇】在阿里云上部署ChatGLM3
前言 好久没写博客了,最近大模型盛行,尤其是ChatGLM3上线,所以想部署试验一下。 本篇只是第一篇,仅仅只是部署而已,没有FINETUNE、没有Langchain更没有外挂知识库,所以从申请资源——>开通虚机——>…...

2023-11-14 mysql-主从复制-相关文档
摘要: 2023-11-14 mysql-主从复制-相关文档 官方文档: MySQL :: MySQL 8.0 Reference Manual :: 17 Replication MySQL :: MySQL 8.0 Reference Manual :: 18 Group Replication 相关参数: mysql> show variables like %repl%; +-----------------------------------------…...
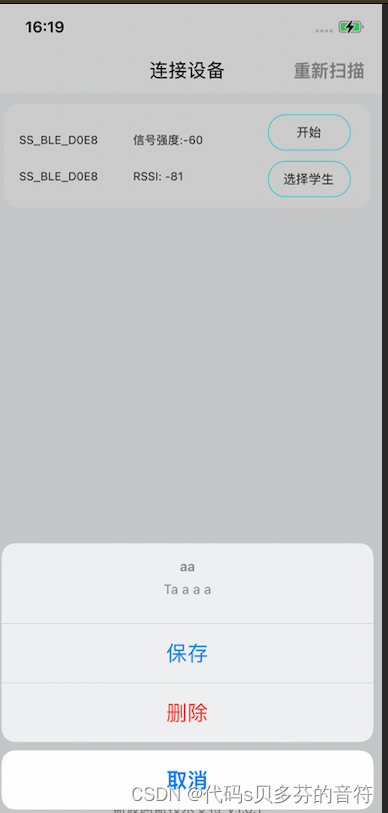
ios 对话框 弹框,输入对话框 普通对话框
1 普通对话框 UIAlertController* alert [UIAlertController alertControllerWithTitle:"a" message:"alert12222fdsfs" pr…...
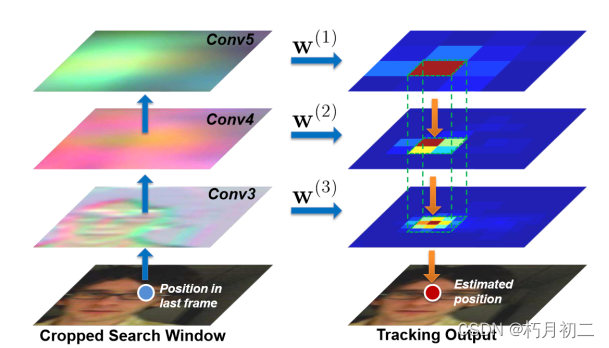
(论文阅读23/100)Hierarchical Convolutional Features for Visual Tracking
文献阅读笔记(分层卷积特征) 简介 题目 Hierarchical Convolutional Features for Visual Tracking 作者 Chao Ma, Jia-Bin Huang, Xiaokang Yang and Ming-Hsuan Yang 原文链接 arxiv.org/pdf/1707.03816.pdf 关键词 Hierarchical convolution…...

基于IGT-DSER智能网关实现GE的PAC/PLC与罗克韦尔(AB)的PLC之间通讯
工业自动化领域的IGT-DSER智能网关模块支持GE、西门子、三菱、欧姆龙、AB等各种品牌的PLC之间通讯(相关资料下载),同时也支持PLC与Modbus协议的工业机器人、智能仪表等设备通讯。网关有多个网口、串口,也可选择WIFI无线通讯。无需编程开发,只…...

创建符合 Web 可访问性标准的 HTML 布局
人们常说网络可访问性是当今万维网的“必须”。“Web 可访问性”一词定义了开发人员需要遵循的一组准则,以使残障人士和 Web 应用程序的交互更加方便。任何网站的内容、UI/UX 设计和布局都应该易于访问。在本文中,Logicify团队为 HTML/CSS 开发人员提供了…...
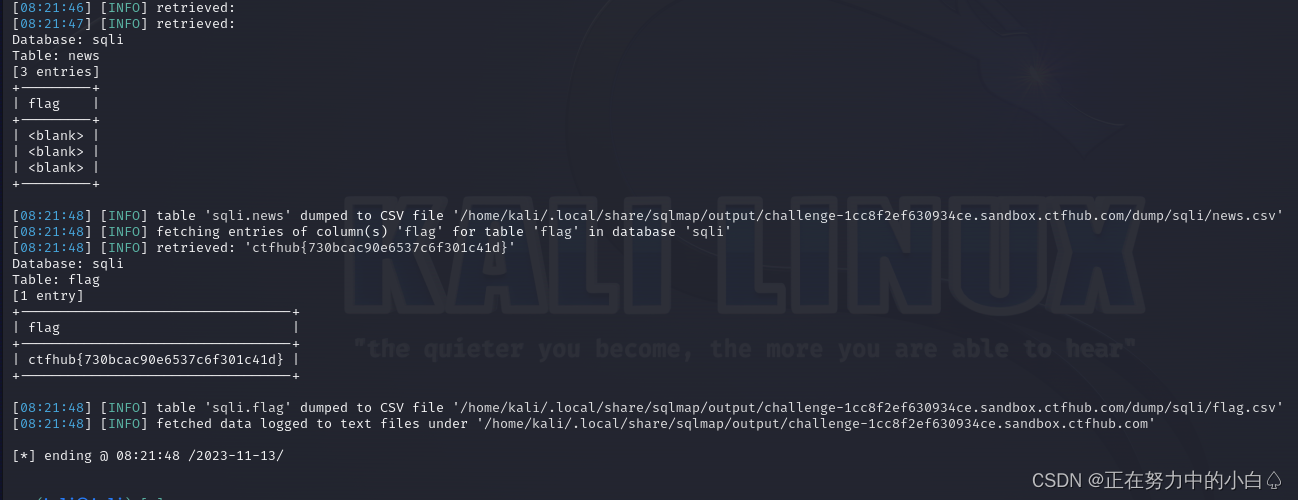
SQL学习(CTFhub)整数型注入,字符型注入,报错注入 -----手工注入+ sqlmap注入
目录 整数型注入 手工注入 为什么要将1设置为-1呢? sqlmap注入 sqlmap注入步骤: 字符型注入 手工注入 sqlmap注入 报错注入 手工注入 sqlmap注入 整数型注入 手工注入 先输入1 接着尝试2,3,2有回显,而3没有回显…...

数字人部署之VITS+Wav2lip数据流转处理以提高实时性
一、模型 VITS模型训练教程VITS-从零开始微调(finetune)训练并部署指南-支持本地云端 Wav2lip是2D数字人,可参考训练嘴型同步模型Wav2Lip PS:以上模型都是开源可用。 二. VITS数据处理问题 VITS模型的输出为一维的numpy类型数据ÿ…...

GPT 学习法:复杂文献轻松的完美理解、在庞大的不确性中找到确定性
GPT 学习法:复杂文献轻松的完美理解、在庞大的不确性中找到确定性 复杂文献 - 基础理解GPT 理解法 - 举例子、归纳、逻辑链推导本质、图示、概念放大器GPT 分析法 - 二分、矩阵、公式、要素、过程 做复杂题:在庞大的不确性中找到确定性思维追踪ÿ…...

前端简单的爱心形状
首先需要创建一个 HTML 文件,然后在其中添加 CSS 样式和 JavaScript 代码。以下是一个简单的示例: 创建一个名为 loveheart.html 的文件 <!DOCTYPE html> <html lang"zh"> <head><meta charset"UTF-8"><…...
)
acwing算法基础之数学知识--求数a的欧拉函数值phi(a)
目录 1 基础知识2 模板3 工程化 1 基础知识 数a的欧拉函数 ϕ ( a ) \phi(a) ϕ(a):表示1~n中与n互质的数的个数。其中两个数互质,是指这两个数的最大公约数为1。 根据定义,我们可以写出如下方法, int gcd(int a, int b) {retu…...
Jenkins的介绍与相关配置
Jenkins的介绍与配置 一.CI/CD介绍 1.CI/CD概念 ①CI 中文意思是持续集成 (Continuous Integration, CI) 是一种软件开发流程,核心思想是在代码库中的每个提交都通过自动化的构建和测试流程进行验证。这种方法可以帮助团队更加频繁地交付软件&#x…...

开源网安受邀参加网络空间安全合作与发展论坛,为软件开发安全建设献计献策
11月10日,在广西南宁举办的“2023网络空间安全合作与发展论坛”圆满结束。论坛在中国兵工学会的指导下,以“凝聚网络空间安全学术智慧,赋能数字经济时代四链融合”为主题,邀请了多位专家及企业代表共探讨网络安全发展与数字经济…...
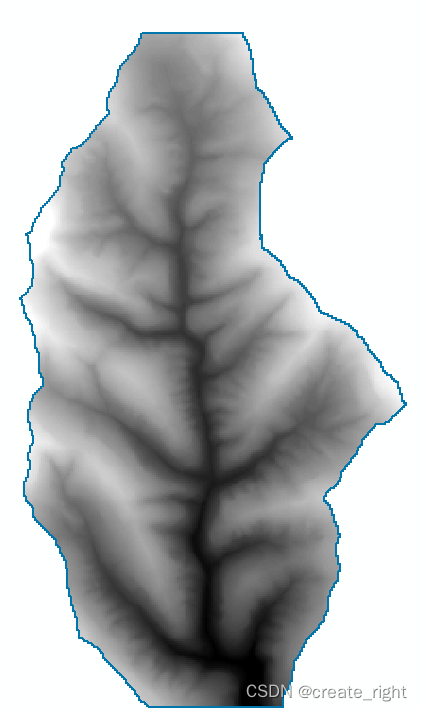
arcgis提取栅格有效边界
方法一:【3D Analyst工具】-【转换】-【由栅格转出】-【栅格范围】 打开一幅栅格数据,利用【栅格范围】工具提取其有效边界(不包含NoData值): 方法二:先利用【栅格计算器】将有效值赋值为1,得到…...

后端接口性能优化分析-问题发现问题定义
👏作者简介:大家好,我是爱吃芝士的土豆倪,24届校招生Java选手,很高兴认识大家📕系列专栏:Spring源码、JUC源码🔥如果感觉博主的文章还不错的话,请👍三连支持&…...

中国首个通过ASIL D认证的IP发布,国产芯片供应商的机会来了
来自智能汽车的“芯”安全需求正在快速爆发。 一方面,随着智能汽车ADAS的快速迭代与逐渐普及化,以及越来越多元化智能座舱功能的快速上车,由此带来的车辆信息安全场景也在与日俱增,例如云端链接、设备身份认证、自动驾驶安全保障…...
[单片机课程设计报告汇总] 单片机设计报告常用硬件元器件描述
[单片机课程设计必看] 单片机设计报告常用描述 硬件设计 AT89C51最小系统 AT89C51是美国ATMEL公司生产的低电压,高性能CMOS16位单片机,片内含4k bytes的可反复擦写的只读程序存储器和128 bytes的随机存取数据存储器,期间采用ATMEL公司的高…...
Docker学习——⑧
文章目录 1、什么是 Docker Compose(容器编排)2、为什么要 Docker Compose?3、Docker Compose 的安装4、Docker Compose 的功能和使用场景5、Docker Compose 文件(docker-compose.yml)5.1 文件语法版本5.2 文件基本结构及常见指令 6、Docker …...

力扣刷题第二十一天--栈与队列
前言 周末玩了两天,s赛看的难受。。。还是和生活对线吧 内容 一、用栈实现队列 232.用栈实现队列 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类&#…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...
