线性代数-Python-05:矩阵的逆+LU分解
文章目录
- 1 矩阵的逆
- 1.1 求解矩阵的逆
- 2 初等矩阵
- 2.1 初等矩阵和可逆性
- 3 矩阵的LU分解
- 3.1 LU分解的实现
1 矩阵的逆

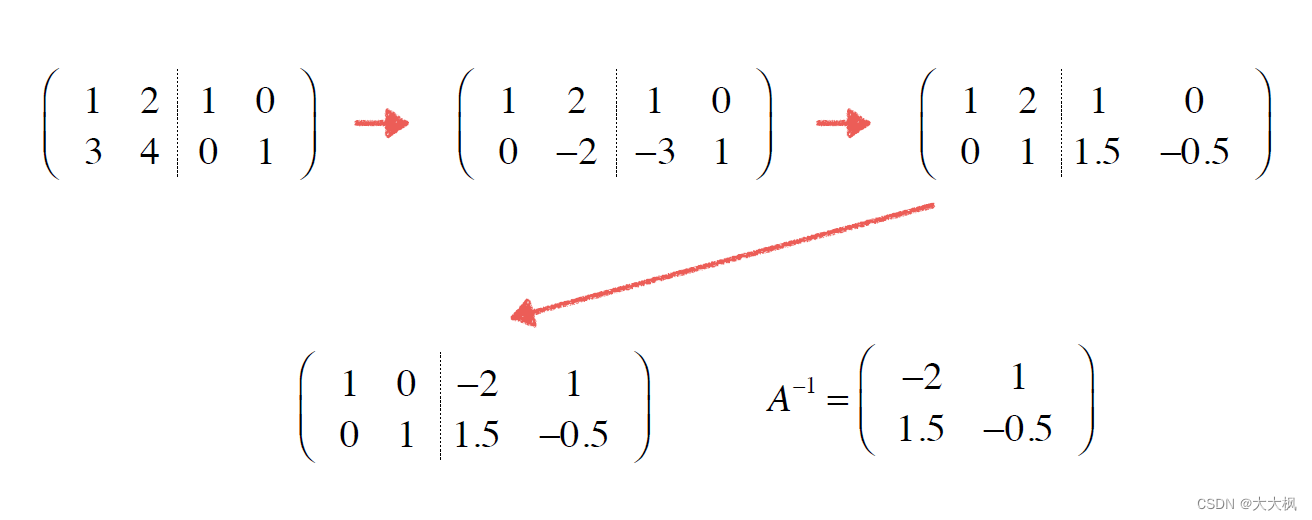
1.1 求解矩阵的逆
def inv(A):if A.row_num() != A.col_num():return Nonen = A.row_num()"""矩阵A+单位矩阵"""ls = LinearSystem(A, Matrix.identity(n))"""对线性系统进行高斯消元,如果没有解,返回none"""if not ls.gauss_jordan_elimination():return None"""高斯消元有解的话,把线性系统的右部分取出,重新构成矩阵,得到矩阵的逆"""invA = [[row[i] for i in range(n, 2*n)] for row in ls.Ab]return Matrix(invA)

2 初等矩阵


2.1 初等矩阵和可逆性
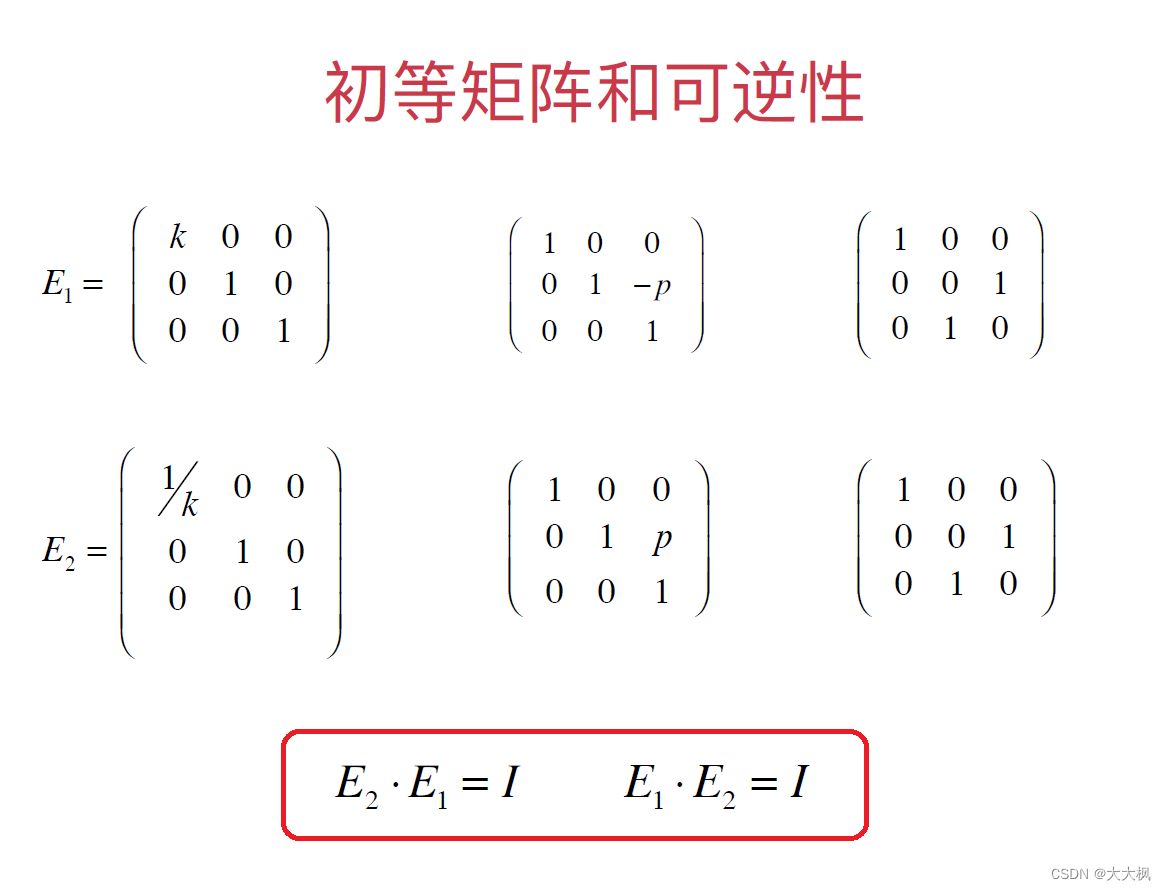

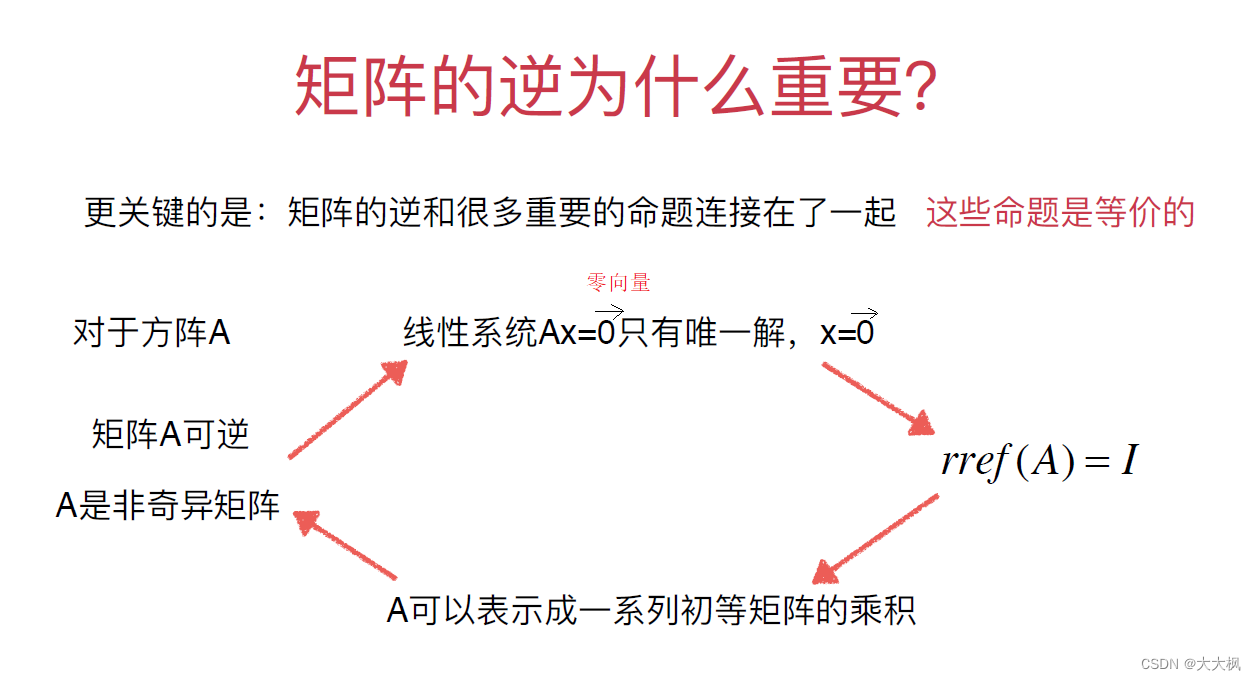
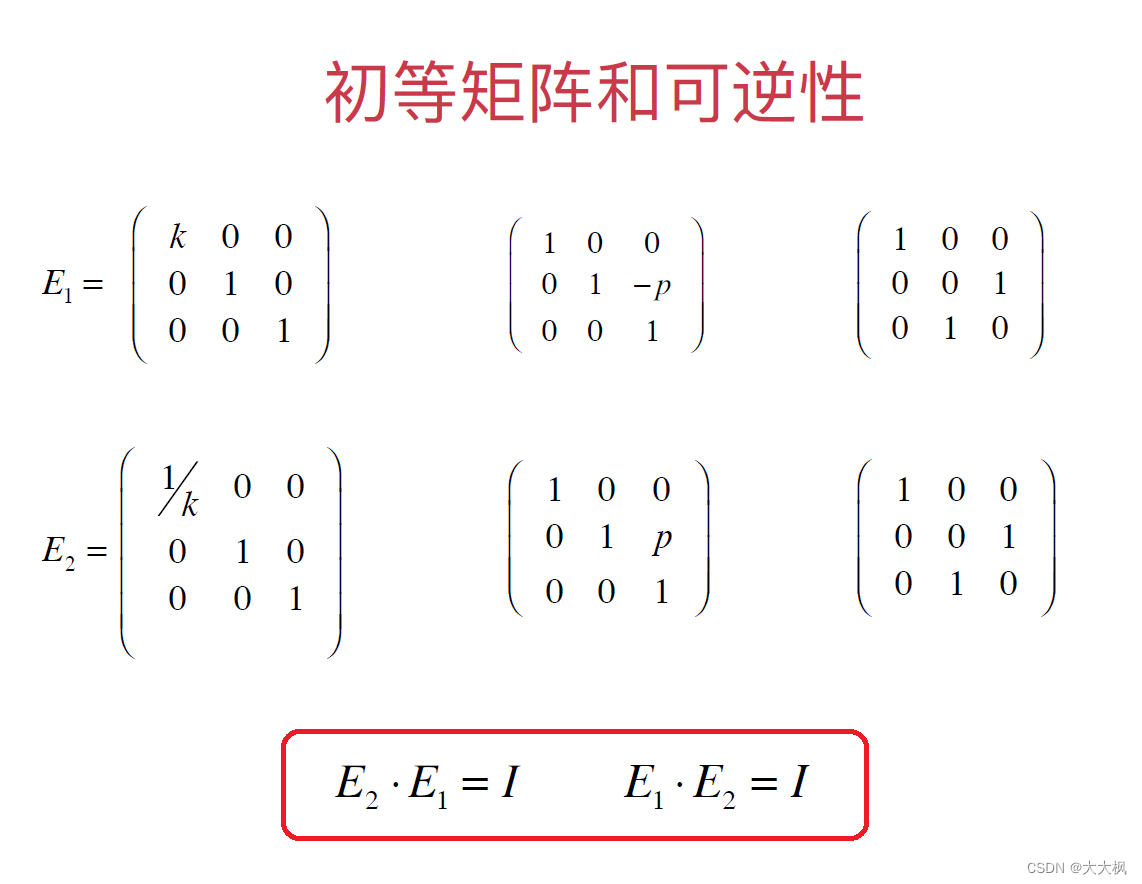
3 矩阵的LU分解
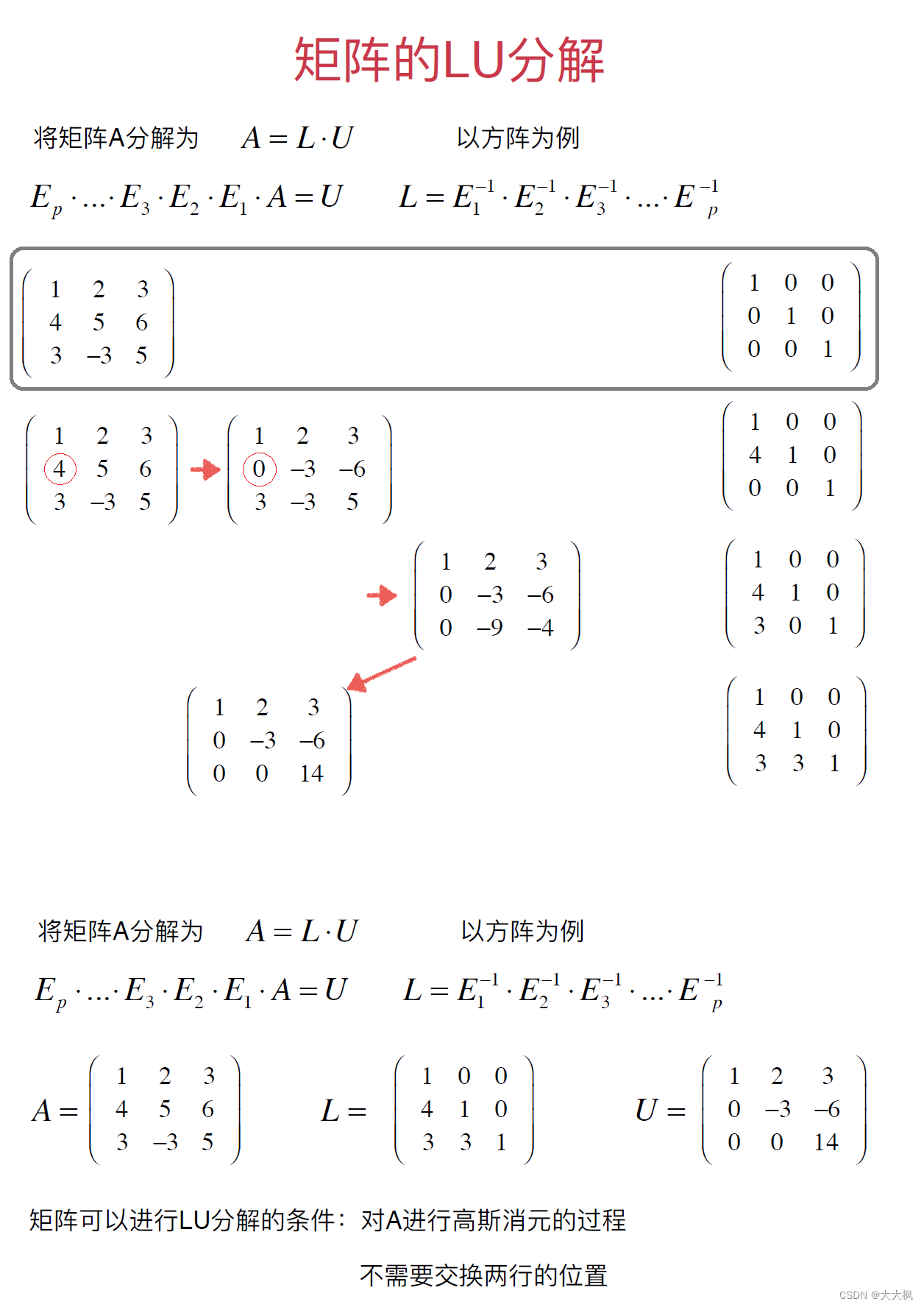
3.1 LU分解的实现
from .Matrix import Matrix
from .Vector import Vector
from ._globals import is_zerodef lu(matrix):assert matrix.row_num() == matrix.col_num(), "matrix must be a square matrix"n = matrix.row_num() """A是原矩阵的副本"""A = [matrix.row_vector(i) for i in range(n)]"""初始化L,使对角线元素为1"""L = [[1.0 if i == j else 0.0 for i in range(n)] for j in range(n)]for i in range(n):"""看A[i][i]位置是否可以是主元"""if is_zero(A[i][i]):return None, Noneelse: """将主元以下的j位置变为0"""for j in range(i + 1, n):p = A[j][i] / A[i][i] """求加减的系数"""A[j] = A[j] - p * A[i] """将第j行的位置经过加减运算变成0"""L[j][i] = p """将L矩阵相应位置变成相应变换的值"""return Matrix(L), Matrix([A[i].underlying_list() for i in range(n)])
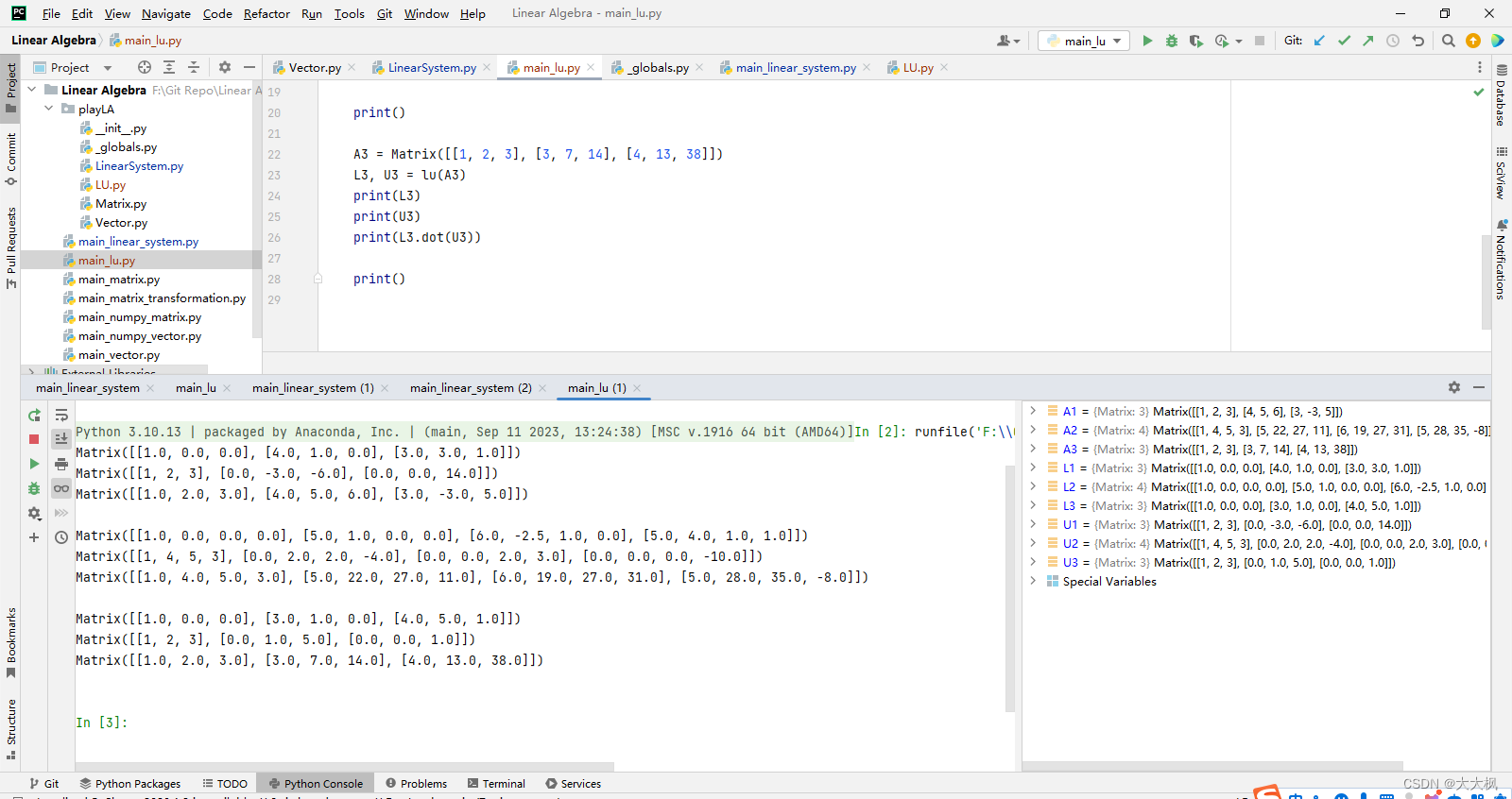
相关文章:

线性代数-Python-05:矩阵的逆+LU分解
文章目录 1 矩阵的逆1.1 求解矩阵的逆 2 初等矩阵2.1 初等矩阵和可逆性 3 矩阵的LU分解3.1 LU分解的实现 1 矩阵的逆 1.1 求解矩阵的逆 def inv(A):if A.row_num() ! A.col_num():return Nonen A.row_num()"""矩阵A单位矩阵"""ls LinearSyste…...

shell实用脚本命令
1. declare declare 命令是一个非常常用的命令之一,它可以用来声明变量的类型和属性,比如变量的作用域、是否只读等等。 一、declare命令的基本用法 declare 命令可以用来声明变量,其最基本的用法如下:declare 变量名 在上面的命…...
STM32——端口复用与重映射概述与配置(HAL库)
文章目录 前言一、什么是端口复用?什么是重映射?有什么区别?二、端口复用配置 前言 本篇文章介绍了在单片机开发过程中使用的端口复用与重映射。做自我学习的简单总结,不做权威使用,参考资料为正点原子STM32F1系列精英…...
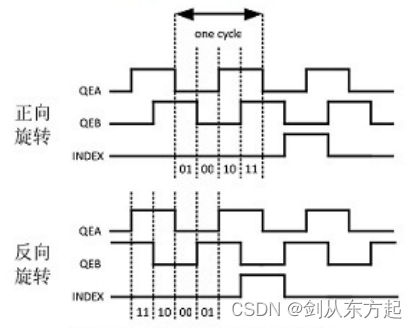
ABZ正交编码 - 异步电机常用的位置信息确定方式
什么是正交编码? ab正交编码器(又名双通道增量式编码器),用于将线性移位转换为脉冲信号。通过监控脉冲的数目和两个信号的相对相位,用户可以跟踪旋转位置、旋转方向和速度。另外,第三个通道称为索引信号&am…...
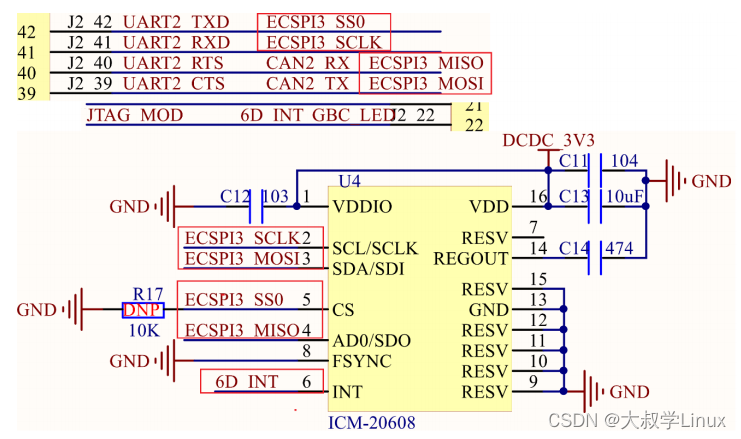
Linux学习第41天:Linux SPI 驱动实验(二):乾坤大挪移
Linux版本号4.1.15 芯片I.MX6ULL 大叔学Linux 品人间百味 思文短情长 本章的思维导图如下: 二、I.MX6U SPI主机驱动分析 主机驱动一般都是由SOC厂商写好的。不作为重点需要掌握的内容。 三、SPI设备驱动编写流程 1、SP…...
黑客泄露 3500 万条 LinkedIn 用户记录
被抓取的 LinkedIn 数据库分为两部分泄露:一部分包含 500 万条用户记录,第二部分包含 3500 万条记录。 LinkedIn 数据库保存了超过 3500 万用户的个人信息,被化名 USDoD 的黑客泄露。 该数据库在臭名昭著的网络犯罪和黑客平台 Breach Forum…...
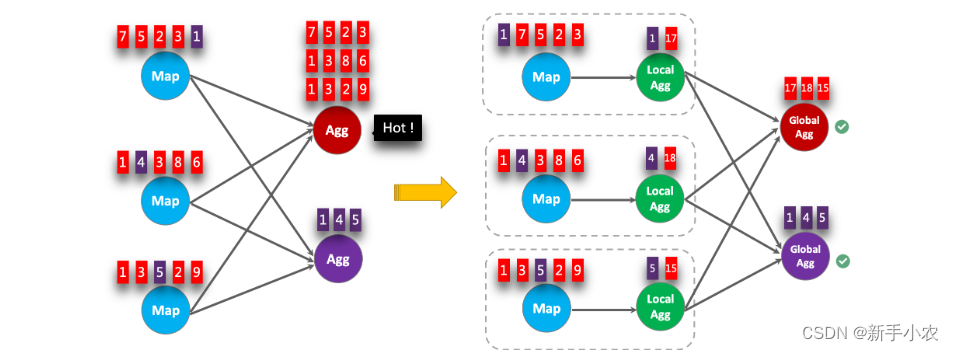
Flink SQL -- 反压
1、测试反压: 1、反压: 指的是下游消费数据的速度比上游产生数据的速度要小时会出现反压,下游导致上游的Task反压。 2、测试反压:使用的是DataGen CREATE TABLE words (word STRING ) WITH (connector datagen,rows-per-second…...
快速入门安装及使用git与svn的区别常用命令
一、导言 1、什么是svn? SVN是Subversion的简称,是一个集中式版本控制系统。与Git不同,SVN没有分布式的特性。在SVN中,项目的代码仓库位于服务器上,团队成员通过向服务器提交和获取代码来实现版本控制。SVN记录了每个…...

超详细介绍如何使用 OpenCV 和 BGS 库进行背景扣除
深入研究这些 CV 系统背后的想法,我们可以观察到,在大多数情况下,初始步骤包含背景减除 (BS),这有助于获得视频流中对象的相对粗略和快速的识别,以便对其进行进一步的精细处理。在当前的文章中,我们将介绍几种在准确性和处理时间 BS 方法方面值得注意的算法:SuBSENSE和基…...

STM32F4、GD32F4 内部硬件CRC使用方法和踩坑实录
背景 某项目用到了IC卡刷卡启动功能,程序中对读取IC卡的相关数据后要进行CRC校验,本文介绍如何在STM32F4 GD32F4 平台上使用标准库函数进行CRC硬件校验。 摘要 本文介绍如何在STM32F4、GD32F4 平台上使用标准库函数进行CRC硬件校验。包括容易出现的问题和解决方法。涉及STM3…...
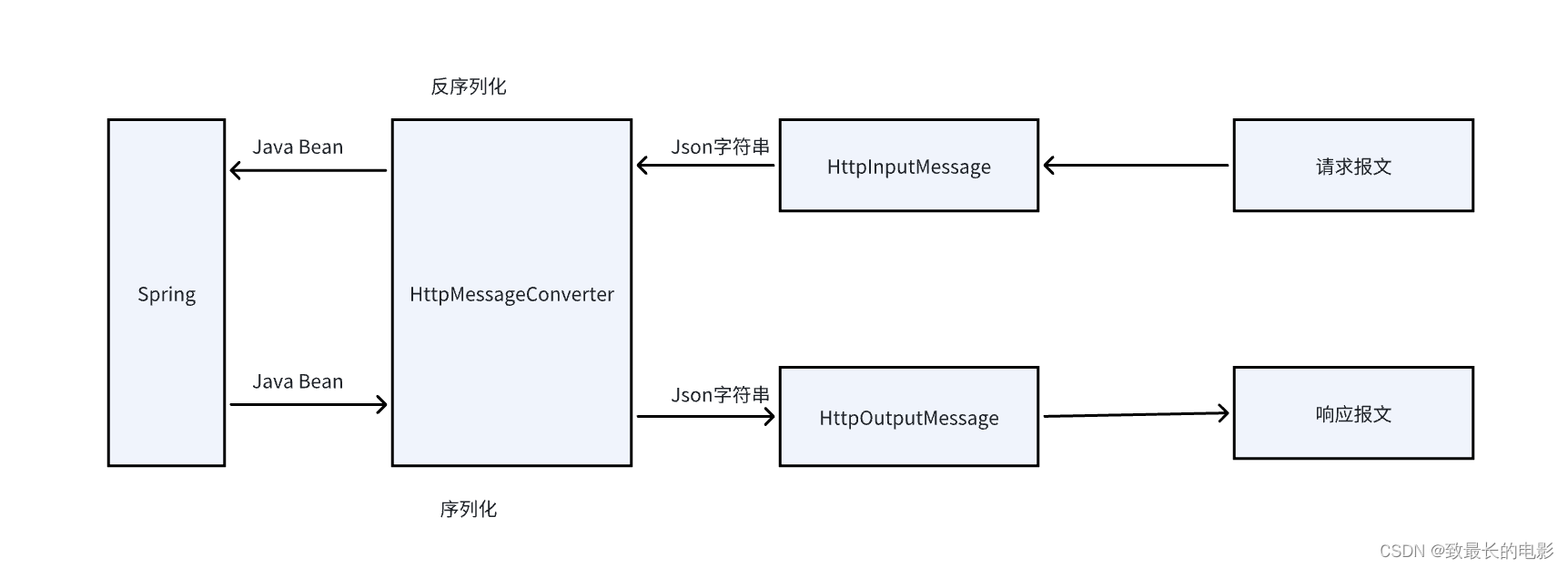
【SpringBoot】序列化和反序列化介绍
一、认识序列化和反序列化 Serialization(序列化)是一种将对象以一连串的字节描述的过程;deserialization(反序列化)是一种将这些字节重建成一个对象的过程。将程序中的对象,放入文件中保存就是序列化&…...

Android 升级软件后清空工厂模式测试进度
Android 升级软件后清空工厂模式测试进度 最近收到项目需求反馈:升级软件后,进入工厂模式测试项,界面显示测试项保留了升级前的测试状态(有成功及失败),需修改升级软件后默认清空测试项测试状态,具体修改参照如下: /…...

Promise原理、以及Promise.race、Promise.all、Promise.resolve、Promise.reject实现;
为了向那道光亮奔过去,他敢往深渊里跳; 于是今天朝着Promise的实现前进吧,写了四个小时,终于完结撒花; 我知道大家没有耐心,当然我也坐的腰疼,直接上代码,跟着我的注释一行行看过去…...
)
mysql---MHA(高可用)
MHA概述 magterhight availabulity :基于主库的高可用环境下,主故障切换基础要求:主从架构 (一主两从)解决mysql的单点故障问题,一旦数据库崩溃,MHA会在0-30s内这东东完成故障切换。复制方式:半…...
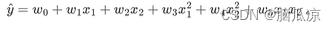
人工智能基础_机器学习032_多项式回归升维_原理理解---人工智能工作笔记0072
现在开始我们来看多项式回归,首先理解多维 原来我们学习的使用线性回归,其实就是一条直线对吧,那个是一维的,我们之前学的全部都是一维的对吧,是一维的,然后是多远的,因为有多个x1,x2,x3,x4... 但是比如我们有一个数据集,是上面这种,的如果用一条直线很难拟合,那么 这个时候,…...

C#截取范围
string[] strs new string[]{"1e2qe","23123e21","3ewqewq","4fewfew","5fsdfds"};var list strs[1..2];Range p 0..3;var list strs[Range];...
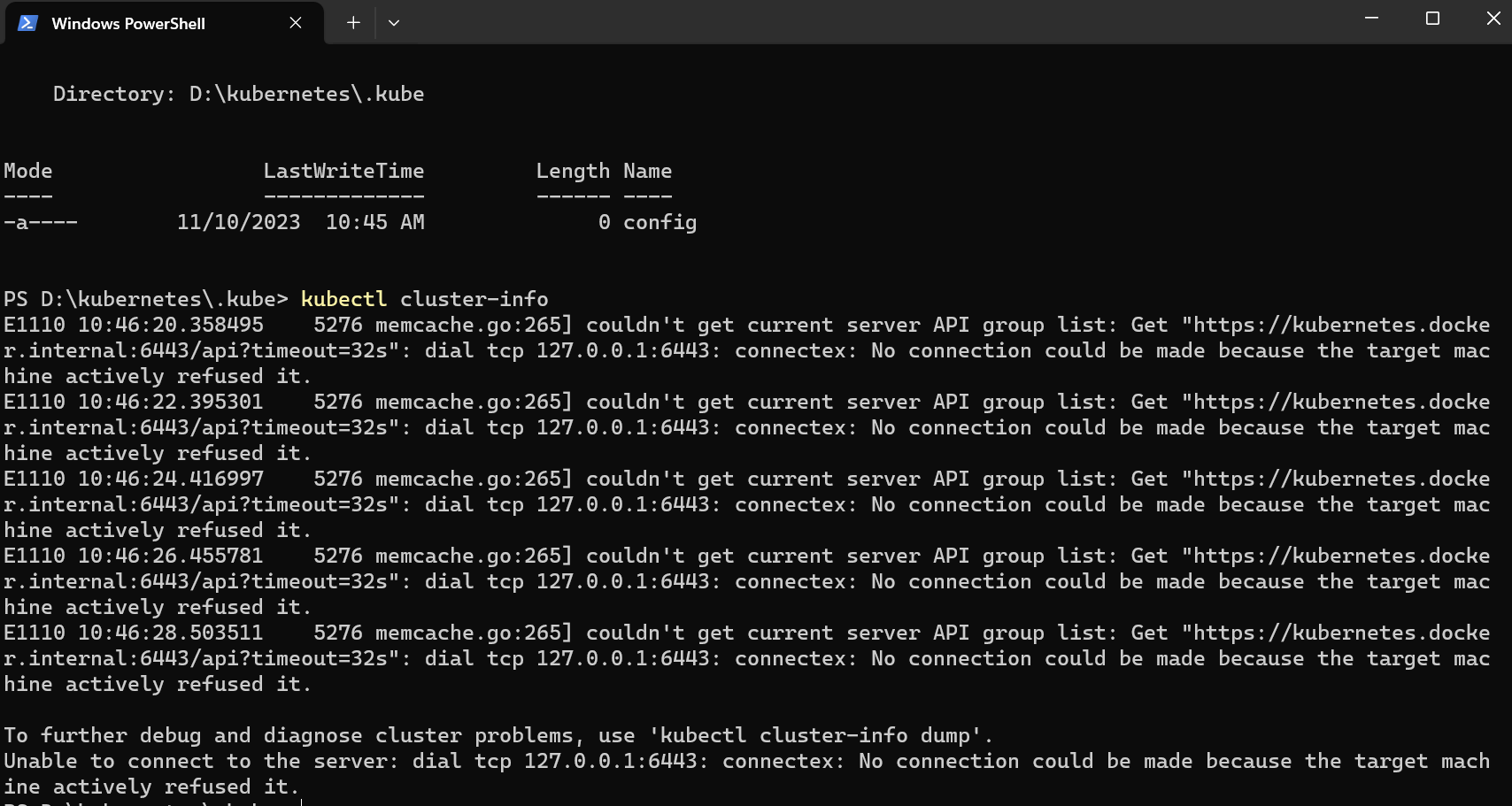
用 winget 在 Windows 上安装 kubectl
目录 kubectl 是什么? 安装 kubectl 以管理员身份打开 PowerShell 使用 winget 安装 kubectl 测试一下,确保安装的是最新版本 导航到你的 home 目录: 验证 kubectl 配置 kubectl 是什么? kubectl 是 Kubernetes 的命令行工…...
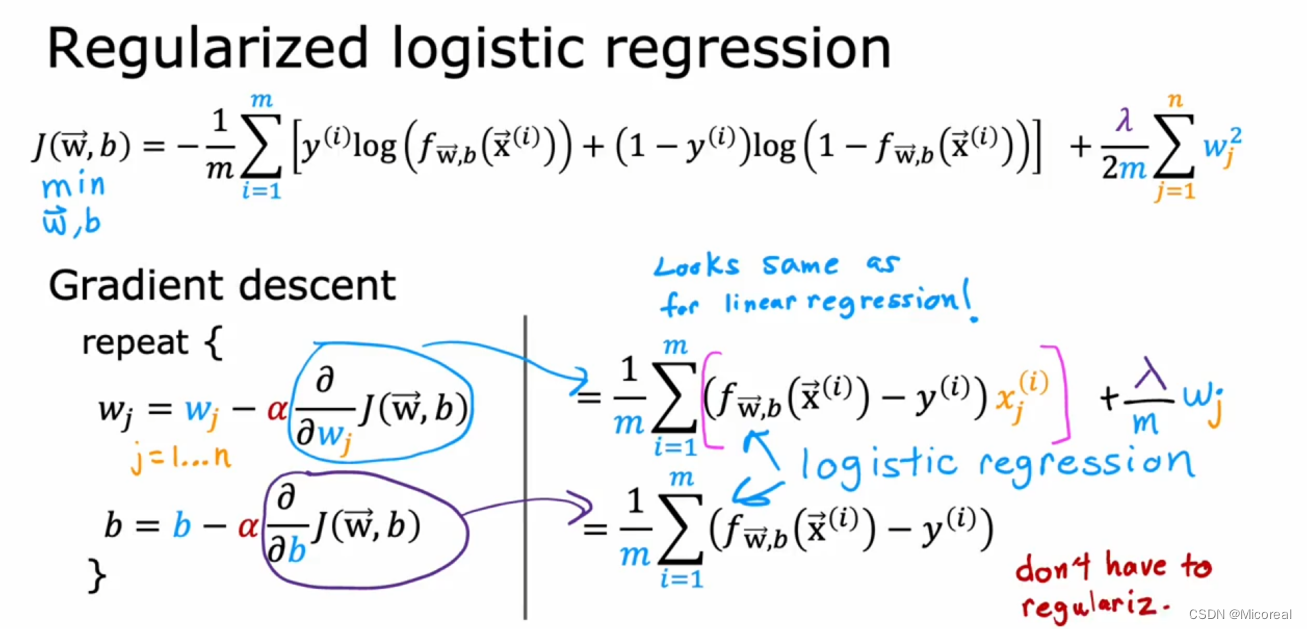
1 Supervised Machine Learning Regression and Classification
文章目录 Week1OverViewSupervised LearningUnsupervised LearningLinear Regression ModelCost functionGradient Descent Week2Muliple FeatureVectorizationGradient Descent for Multiple RegressionFeature ScalingGradient DescentFeature EngineeringPolynomial Regress…...

Antv/G2 折线图 DataSet 数据展开成指定格式
DataSet 文档 G2 3.2 DataSet 文档 Demo: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><m…...
物理问题中常见的分析问题----什么样的函数性质较好
物理问题中常见的积分符号位置交换问题 重极限与累次极限 高数下的定义 累次极限:求极限时需要遵循一定的顺序重极限:任意方向趋于的极限 两者之间的关系: 两者没啥关系存在累次极限存在而不相等的函数...... 求和符号与积分符号互换--逐项积…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
