【数学】Pair of Topics—CF1324D
Pair of Topics—CF1324D
思路
很明显,需要对 a i + a j > b i + b j a_i + a_j > b_i + b_j ai+aj>bi+bj 化简:
a i − b i > b j − a j a_i - b_i > b_j - a_j ai−bi>bj−aj
a i − b i > − ( a j − b j ) a_i - b_i > -(a_j - b_j) ai−bi>−(aj−bj)
令 c i = a i − b i c_i = a_i - b_i ci=ai−bi,则:
c i > − c j c_i > -c_j ci>−cj
c i + c j > 0 c_i + c_j > 0 ci+cj>0
所求变成:
满足 i < j i < j i<j 且 c i + c j > 0 c_i + c_j > 0 ci+cj>0 的数量。
可以看出,如果没有 i < j i < j i<j 这个要求,那么我们可以对 c c c 排序,遍历 i i i,对于每一个 c i c_i ci 用二分求出满足 c i + c j > 0 c_i + c_j > 0 ci+cj>0 的数量,再求和即可。
其实我们恰恰可以上边的方法求出答案 r e s res res,然后再执行 r e s / = 2 res~/=~2 res /= 2 就是在约束条件 i < j i < j i<j 下的答案。
因为我们用这个方法遍历每一个 c i c_i ci 的时候,都多计算了其中 i ′ > j ′ i' > j' i′>j′ 且 c i ′ + c j ′ > 0 c_i' + c_j' > 0 ci′+cj′>0 的数量,而这样的一对 c i ′ , c j ′ c_i', c_j' ci′,cj′ 在 i ( 遍历过程中的 i ) = j ′ ( 当前的 j ′ ) i(遍历过程中的i) = j'(当前的j') i(遍历过程中的i)=j′(当前的j′) 时都是同时满足两个条件的。所以我们多计算的数量等于应该计算的数量,最终 r e s res res 除以 2 2 2 就是本题正确的答案。
例如, i = 3 , j = 2 , c i = 666 , c j = − 666 i = 3, j = 2, c_i = 666, c_j = -666 i=3,j=2,ci=666,cj=−666,我们在用上百年那个方法的时候会将这种情况也计算在内。但如果将 i , j i, j i,j 对调,我们发现 i = 2 , j = 3 , c i = − 666 , c j = 666 i = 2, j = 3, c_i = -666, c_j = 666 i=2,j=3,ci=−666,cj=666 是同时满足两个条件的。同理,每一个满足两个条件的 i , j i, j i,j 都会其将 i , j i, j i,j 对调后的 i , j i, j i,j 都会错误地被当做正确情况计算在内。
C o d e Code Code
#include <bits/stdc++.h>
#define int long long
#define sz(a) ((int)a.size())
#define all(a) a.begin(), a.end()
using namespace std;
using PII = pair<int, int>;
using i128 = __int128;
const int N = 2e5 + 10;int n;
int c[N];void solve(int Case) {cin >> n;for (int i = 1; i <= n; i ++) cin >> c[i];for (int i = 1; i <= n; i ++) {int b; cin >> b;c[i] -= b;}sort(c + 1, c + n + 1);int res = 0;for (int i = 1; i <= n; i ++) {int l = 1, r = n;while (l < r) {int mid = (l + r) / 2;if (c[i] + c[mid] > 0) {r = mid;} else {l = mid + 1;}}if (c[i] + c[l] > 0) {res += (n - l + 1) - (l <= i);}}cout << " ";cout << res / 2 << "\n";
}signed main() {cin.tie(0)->ios::sync_with_stdio(false);int T = 1;
// cin >> T; cin.get();int Case = 0;while (++ Case <= T) solve(Case);return 0;
}
相关文章:

【数学】Pair of Topics—CF1324D
Pair of Topics—CF1324D 思路 很明显,需要对 a i a j > b i b j a_i a_j > b_i b_j aiaj>bibj 化简: a i − b i > b j − a j a_i - b_i > b_j - a_j ai−bi>bj−aj a i − b i > − ( a j − b j ) a_…...
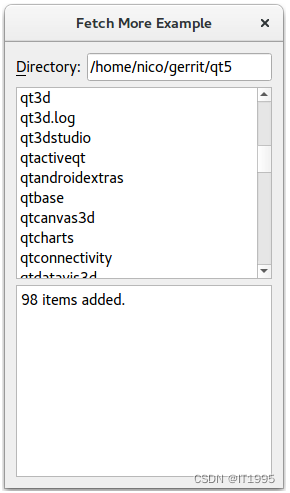
Qt文档阅读笔记-Fetch More Example解析
Fetch More Example这个例子说明了如何在视图模型上添加记录。 这个例子由一个对话框组成,在Directory的输入框中,可输入路径信息。应用程序会载入路径信息的文件信息等。不需要按回车键就能搜索。 当有大量数据时,需要对视图模型进行批量增…...

QtC++与QTableView详解
介绍 QTableView 是 Qt 框架中用于显示表格数据的视图控件,它是 QAbstractItemView 类的子类。QTableView 通常与 QStandardItemModel 或者自定义的数据模型一起使用,用于展示二维表格型数据。以下是对 QTableView 的详细讲解和在 Qt 中的作用ÿ…...

HG/T 6002-2022 氟树脂粉末涂料检测
氟树脂粉末涂料是指以三氟氯乙烯-乙烯基醚、四氟乙烯-乙烯基醚等交联型氟树脂或聚偏二氟乙烯PVDF树脂为主要成膜物质,可加入颜料、填料、助剂、固化剂等制成的粉末涂料,主要用于铝型材、幕墙金属板、家电等表面的装饰和保护。 HG/T 6002-2022 氟树脂粉末…...

【java】idea可以连接但看不到database相关的files
问题 idea右侧有database工具栏,但点击没有在recent files看到数据库相关文件 问题排查 点击 help-> show log in explorer查看日志 发现显示 2023-11-13 10:28:09,694 [1244376] INFO - #c.i.c.ComponentStoreImpl - Saving appDebuggerSettings took 22…...

信驰达科技加入车联网联盟(CCC),推进数字钥匙发展与应用
CCC)的会员。 图 1 深圳信驰达正式成为车联网联盟(CCC)会员 车联网联盟(CCC)是一个跨行业组织,致力于推动智能手机与汽车连接解决方案的技术发展。CCC涵盖了全球汽车和智能手机行业的大部分企业,拥有150多家成员公司。CCC成员公司包括智能手机和汽车制造…...

p9 Eureka-搭建eureka服务
1.在user-service项目引入spring-cloud-starter-netflix-eureka-client的依赖 <dependencies><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-eureka-server</artifactId></depen…...
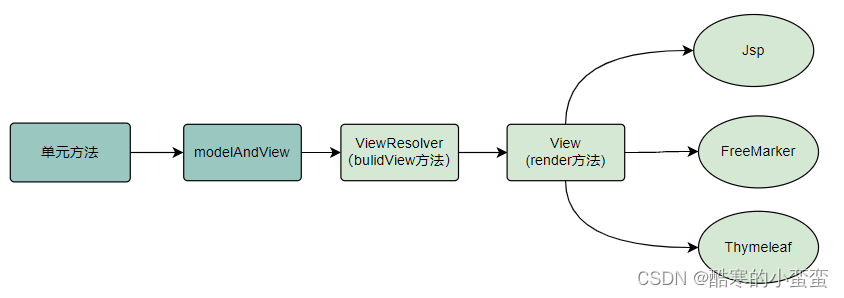
阶段七-Day01-SpringMVC
一、Sping MVC的介绍 1. 使用Front(前端)设计模式改写代码 1.1 目前我们的写法 目前我们所写的项目,持久层、业务层的类都放入到Spring容器之中了。他们之间需要注入非常方便,只需要通过Autowired注解即可。 但是由于Servlet整个生命周期都是被Tomca…...
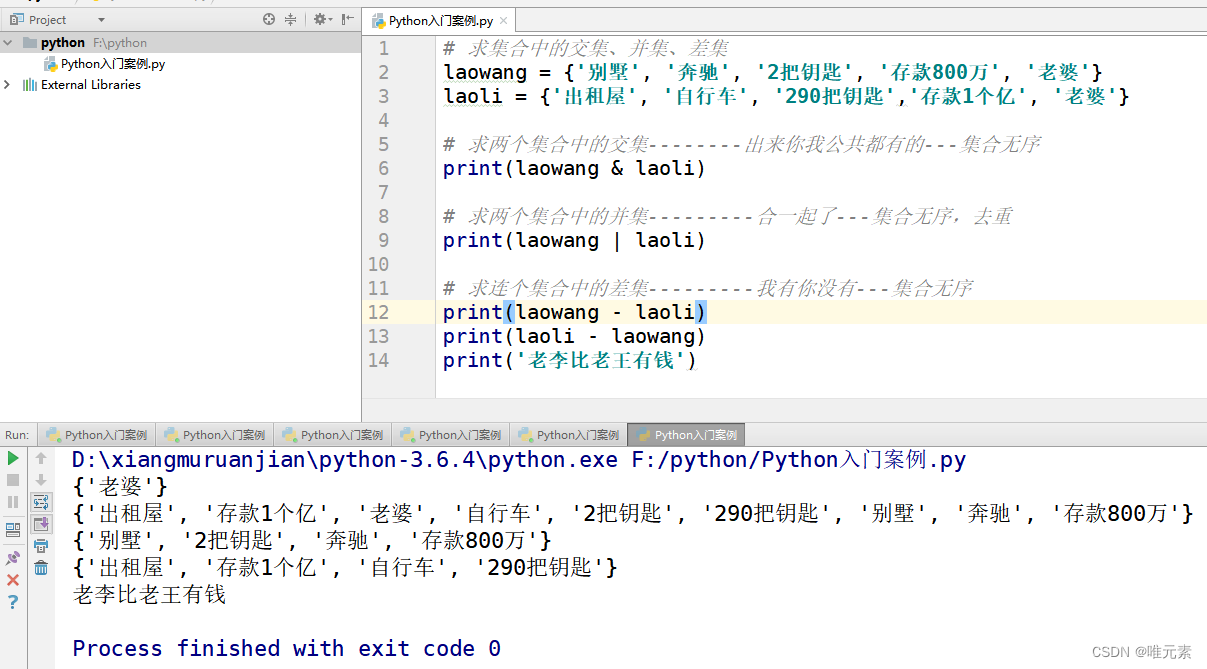
Python---集合中的交集 、并集 | 与差集 - 特性
用 & 来求两个集合的交集:-----键盘上的7上的符号,shift 7 同时按 用 | 来求两个集合的并集: -----键盘上的7上的符号,shift 同时按(就是enter键上面那个|\ ) 用 - 来求两个集合的差集ÿ…...

C++调用lua脚本,包括全局函数绑定、类绑定,十分钟快速掌握
系列文章目录 lua调用C/C的函数,十分钟快速掌握 C调用lua脚本,包括全局函数绑定、类绑定,十分钟快速掌握 系列文章目录摘要环境使用步骤码代码自定义函数多返回值变长参数 自定义类test_sol2.lua内容 程序输出 摘要 在这个快节奏的技术博客…...

快乐数[简单]
优质博文:IT-BLOG-CN 一、题目 编写一个算法来判断一个数n是不是快乐数。「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程直到这个数变为1,也可能是无限循环但始终变不到1。如…...

Spring源码阅读-ClassPathXmlApplicationContext
第一步:new一个ClassPathXmlApplicationContext对象 ClassPathXmlApplicationContext xmlContext new ClassPathXmlApplicationContext("mylearn.xml"); 第二步:调用构造方法 public ClassPathXmlApplicationContext(String configLocatio…...

考研分享第2期 | 中央财经大学管理科学跨考北大软微金融科技406分经验分享
一、个人信息 本科院校:中央财经大学 管理科学与工程学院 管理科学专业 上岸院校:北京大学 软件与微电子学院 金融科技专业硕士 考试科目: 初试:思想政治理论 英语一 数学二 经济学综合 面试考察范围广,包括英语自…...

Linux安装java jdk配置环境 方便查询
编辑/etc/profile文件: vim /etc/profile 在文件尾部添加如下配置: export JAVA_HOME/usr/local/jdk1.8.0_161/ export CLASSPATH.: J A V A H O M E / j r e / l i b / r t . j a r : JAVA_HOME/jre/lib/rt.jar: JAVAHOME/jre/lib/rt.jar:JAVA_HOME/l…...

惊群效应之Nginx处理
文章目录 惊群概述Nginx 解决方案之锁的设计锁结构体原子锁创建原子锁获取原子锁实现原子锁释放 Nginx 解决方案之惊群效应总结: 惊群概述 在说nginx前,先来看看什么是“惊群”?简单说来,多线程/多进程(linux下线程进…...

SpringBoot整合Ldap--超详细方法讲解
LADP概述 LDAP(轻量目录访问协议)是一种用于访问和维护分布式目录信息服务的协议。目录服务是一种存储和检索信息的服务,通常用于存储组织内的用户信息、组织结构、网络设备等数据。LDAP是一种轻量级的协议,设计用于在目录中进行查…...

【工程实践】Docker使用记录
前言 服务上线经常需要将服务搬到指定的服务器上,经常需要用到docker,记录工作中使用过dcoker指令。 1.写Dockerfile 1.1 全新镜像 FROM nvidia/cuda:11.7.1-devel-ubuntu22.04ENV WORKDIR/data/Qwen-14B-Chat WORKDIR $WORKDIR ADD . $WORKDIR/RUN ap…...

FreeSwitch安装视频
文章目录 序言Centos7安装FreeSwitch-1.6 序言 学习资料来源《FreeSWITCH权威指南》-作者杜金房这本书。我是2022年6月毕业的,偶然的机会接触到FreeSWITCH,FreeSWITCH纯属个人爱好,进行笔记整理。也一直希望有机会可以参与FreeSWITCH相关工作…...
SpringBoot3+Vue3+Mysql+Element Plus完成数据库存储blob类型图片,前端渲染后端传来的base64类型图片
前言 如果你的前后端分离项目采用SpringBoot3Vue3Element Plus,且在没有OSS(对象存储)的情况下,使用mysql读写图片(可能不限于图片,待测试)。 耗时三天,在踩了无数雷后,…...

攻略 | 参与Moonbeam Ignite Ecosystem Tour
Moonbeam联合Moonwell和Beamswap一起举办社区链上活动,旨在让社区用户通过任务来探索Moonbeam、Moonwell、Beamswap平台。在了解如何使用的同时,参与任务挑战还有机会分得 1700 USDC 奖池 🎁 的奖励!我已经完成全部任务࿰…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
