[量子计算与量子信息] 2.1 线性代数
2.1 线性代数
符号对照表

量子力学中,向量使用 ∣ ψ ⟩ \ket \psi ∣ψ⟩ (ket)来表示,可以理解为一个列向量。其对偶向量为 ⟨ ψ ∣ \bra \psi ⟨ψ∣ ,可以理解为行向量。
向量空间中零向量直接用 0 0 0 表示, ∣ 0 ⟩ \ket{0} ∣0⟩ 已有了其他含义。
2.1.1 基与线性无关
向量空间中的一个生成集是一组向量 ∣ v 1 ⟩ , ∣ v 2 ⟩ , . . . , ∣ v n ⟩ \ket{v_1},\ket{v_2},...,\ket{v_n} ∣v1⟩,∣v2⟩,...,∣vn⟩,空间中的任意向量 ∣ v ⟩ \ket{v} ∣v⟩ 均能使用该组向量的线性组合来表示,即 ∣ v ⟩ = ∑ i a i ∣ v i ⟩ \ket{v} = \sum_i a_i \ket{v_i} ∣v⟩=∑iai∣vi⟩。
线性相关
一组非零向量 ∣ v 1 ⟩ , ∣ v 2 ⟩ , . . . , ∣ v n ⟩ \ket{v_1},\ket{v_2},...,\ket{v_n} ∣v1⟩,∣v2⟩,...,∣vn⟩,如果存在一组复数 a 1 , a 2 , . . . , a n a_1, a_2,...,a_n a1,a2,...,an,其中至少对一个 i i i ,有 a i ≠ 0 a_i \ne 0 ai=0,
a 1 ∣ v 1 ⟩ + a 2 ∣ v 2 ⟩ + . . . + a n ∣ v n ⟩ = 0 a_1 \ket{v_1} + a_2 \ket{v_2} + ... + a_n \ket{v_n} = 0 a1∣v1⟩+a2∣v2⟩+...+an∣vn⟩=0
成立。反之,则是线性无关的。
对于任意两个线性无关的向量组如果都是向量空间 V V V 的生成集,则必然包含相同数目的元素。
2.1.2 线性算子与矩阵
定义
任意对输入是线性的函数 A : V → W A:V\rightarrow W A:V→W,满足:
A ( ∑ i a i ∣ ψ ⟩ ) = ∑ i a i A ∣ ψ ⟩ A(\sum_i a_i \ket{\psi}) = \sum_i a_i A \ket \psi A(i∑ai∣ψ⟩)=i∑aiA∣ψ⟩
线性算子与矩阵是等价的。
设 A : V → W A: V \rightarrow W A:V→W 是向量空间 V V V 和 W W W 之间的一个线性算子,设 ∣ v 1 ⟩ , ∣ v 2 ⟩ , . . . ∣ v m ⟩ \ket{v_1},\ket{v_2},...\ket{v_m} ∣v1⟩,∣v2⟩,...∣vm⟩ 是 V V V 的一个基而 ∣ w 1 ⟩ , ∣ w 2 ⟩ , . . . , ∣ w n ⟩ \ket{w_1},\ket{w_2},...,\ket{w_n} ∣w1⟩,∣w2⟩,...,∣wn⟩ 是 W W W 的一个基。于是存在
A ∣ v j ⟩ = ∑ i A i j ∣ w i ⟩ A \ket{v_j} = \sum_i A_{ij} \ket{w_i} A∣vj⟩=i∑Aij∣wi⟩
2.1.3 Pauli 阵

2.1.4 内积
内积定义
存在从 V × V V \times V V×V 到 C C C 的函数 ( ∙ , ∙ ) (\bullet,\bullet) (∙,∙),满足:
- ( ∙ , ∙ ) (\bullet,\bullet) (∙,∙) 对第二个自变量是线性的,即
( ∣ v ⟩ , ∑ i λ i ∣ w i ⟩ ) = ∑ i λ i ( ∣ v ⟩ , ∣ w i ⟩ ) (\ket{v}, \sum_i \lambda_i \ket{w_i}) = \sum_i \lambda_i(\ket v,\ket{w_i}) (∣v⟩,i∑λi∣wi⟩)=i∑λi(∣v⟩,∣wi⟩)
-
( ∣ v ⟩ , ∣ w ⟩ ) = ( ∣ w ⟩ , ∣ v ⟩ ) ∗ (\ket v, \ket w) = (\ket w, \ket v)^* (∣v⟩,∣w⟩)=(∣w⟩,∣v⟩)∗,即 ⟨ v ∣ w ⟩ = ( ⟨ w ∣ v ⟩ ) ∗ \braket{v|w} = (\braket{w|v})^* ⟨v∣w⟩=(⟨w∣v⟩)∗
-
( ∣ v ⟩ , ∣ v ⟩ ) ≥ 0 (\ket v, \ket v) \ge 0 (∣v⟩,∣v⟩)≥0, 当且仅当 ∣ v ⟩ = 0 \ket v = 0 ∣v⟩=0 时取等号
例如, C n C^n Cn 具有如下定义的一个内积:
( ( y 1 , y 2 , . . . y n ) , ( z 1 , z 2 , . . . , z n ) ) = ∑ i y i ∗ z i = [ y 1 ∗ , y 2 ∗ , . . . , y n ∗ ] [ z 1 z 2 ⋮ z n ] ((y_1,y_2,...y_n),(z_1,z_2,...,z_n)) = \sum_i y_i^*z_i = [y_1^*,y_2^*,...,y_n^*] \begin{bmatrix} z_1 \\ z_2 \\ \vdots \\ z_n \end{bmatrix} ((y1,y2,...yn),(z1,z2,...,zn))=i∑yi∗zi=[y1∗,y2∗,...,yn∗] z1z2⋮zn
带内积的向量空间称为内积空间,即 Hilbert 空间。
正交
如果向量 ∣ v ⟩ \ket v ∣v⟩ 和 ∣ w ⟩ \ket w ∣w⟩ 的内积为0,则称它们正交。
范数
∥ ∣ v ⟩ ∥ = ⟨ v ∣ v ⟩ \Vert \ket v \Vert = \sqrt{\braket{v|v}} ∥∣v⟩∥=⟨v∣v⟩
如果 ∥ ∣ v ⟩ ∥ = 1 \Vert \ket{v} \Vert = 1 ∥∣v⟩∥=1,则称其为单位向量,或归一化的。
对任意非零向量 ∣ v ⟩ \ket v ∣v⟩,向量除以其范数,称为向量的归一化。
从现在起,提到线性算子的矩阵表示时,我们总是指相对标准正交的输入输出基的矩阵表示,同时约定当线性算子的输入输出空间相同时,除非特别说明,输入输出基也取相同。
对偶向量可以当作一个行向量,其分量对于 ∣ v ⟩ \ket v ∣v⟩ 列向量表示的分量的复共轭,即 ⟨ v ∣ = [ v 1 ∗ , v 2 ∗ , . . . , v n ∗ ] \bra v = [v_1^*,v_2^*,...,v_n^*] ⟨v∣=[v1∗,v2∗,...,vn∗].
外积
设 ∣ v ⟩ \ket v ∣v⟩ 是内积空间 V V V 中的向量,而 ∣ w ⟩ \ket w ∣w⟩ 是内积空间 W W W 中的向量,定义 ∣ w ⟩ ⟨ v ∣ \ket w \bra v ∣w⟩⟨v∣ 为从 V V V 到 W W W 的线性算子:
( ∣ w ⟩ ⟨ v ∣ ) ( ∣ v ′ ⟩ ) = ∣ w ⟩ ⟨ v ∣ v ′ ⟩ = ⟨ v ∣ v ′ ⟩ ∣ w ⟩ (\ket w \bra v)(\ket {v^{'}}) = \ket w \braket {v|v^{'}} = \braket {v|v^{'}} \ket w (∣w⟩⟨v∣)(∣v′⟩)=∣w⟩⟨v∣v′⟩=⟨v∣v′⟩∣w⟩
完备性关系
设 i i i 为向量空间 V V V 的任意标准正交基,任意向量 ∣ v ⟩ \ket v ∣v⟩ 可写成 ∣ v ⟩ = ∑ i v i ∣ i ⟩ \ket v = \sum_i v_i \ket i ∣v⟩=∑ivi∣i⟩, v i v_i vi 是一组复数。注意到 ⟨ i ∣ v ⟩ = v i \braket {i|v} = v_i ⟨i∣v⟩=vi,于是
( ∑ i ∣ i ⟩ ⟨ i ∣ ) ∣ v ⟩ = ∑ i ∣ i ⟩ ⟨ i ∣ v ⟩ = ∑ i v i ∣ i ⟩ = ∣ v ⟩ (\sum_i \ket i \bra i) \ket v = \sum_i \ket i \braket {i | v} = \sum_i v_i \ket i = \ket v (i∑∣i⟩⟨i∣)∣v⟩=i∑∣i⟩⟨i∣v⟩=i∑vi∣i⟩=∣v⟩
故有:
∑ i ∣ i ⟩ ⟨ i ∣ = I \sum_i \ket i \bra i = I i∑∣i⟩⟨i∣=I
完备性关系的一个应用是把任意线性算子表示成外积形式。设 A : V → W A: V \rightarrow W A:V→W 是一个线性算子, ∣ v i ⟩ \ket{v_i} ∣vi⟩ 是 V V V 的一个标准正交基,且 w j w_j wj 是 W W W 的一个标准正交基,两次应用完备性关系得到:
A = I w A I v A = I_w A I_v A=IwAIv
= ∑ i j ∣ w j ⟩ ⟨ w j ∣ A ∣ v i ⟩ ⟨ v i ∣ = \sum_{ij}\ket{w_j} \bra{w_j} A \ket{v_i} \bra{v_i} =ij∑∣wj⟩⟨wj∣A∣vi⟩⟨vi∣
= ∑ i j ⟨ w j ∣ A ∣ v i ⟩ ∣ w j ⟩ ⟨ v i ∣ = \sum_{ij} \bra{w_j} A \ket{v_i} \ket{w_j}\bra{v_i} =ij∑⟨wj∣A∣vi⟩∣wj⟩⟨vi∣
这就是 A A A 的外积表示,从此式也可以看出相对输入基 ∣ v i ⟩ \ket{v_i} ∣vi⟩ 和 输出基 ∣ w ⟩ j \ket w_j ∣w⟩j , A A A 的第 i i i 列第 j j j 行元素是 ⟨ w j ∣ A ∣ v i ⟩ \bra{w_j}A\ket{v_i} ⟨wj∣A∣vi⟩.
2.1.5 特征向量和特征值
线性算子 A A A 在向量空间上的特征向量(本征向量,eigenvector)指非零的向量 ∣ v ⟩ \ket v ∣v⟩,使得 A ∣ v ⟩ = v ∣ v ⟩ A \ket v = v \ket v A∣v⟩=v∣v⟩,其中 v v v 是一个复数,称为 A A A 对应于 ∣ v ⟩ \ket v ∣v⟩ 的特征值(本征值,eigenvalue)。通常为方便起见,采用同一个记号 v v v 表示特征向量的标号和特征值。
向量空间 V V V 上算子 A A A 的对角表示是具有形式 A = ∑ i λ i ∣ i ⟩ ⟨ i ∣ A = \sum_i \lambda_i \ket i \bra i A=∑iλi∣i⟩⟨i∣ 的一个表示,其中向量组 ∣ i ⟩ \ket i ∣i⟩ 是 A A A 的特征向量构成的标准正交向量组,对应的特征值为 λ i \lambda_i λi。
如果一个算子有对角表示,它被称为可对角化。原矩阵与对角化后的矩阵是相似的。
当本征空间大于一维时,称为简并,即同一特征值对应多个线性无关的特征向量。
相似矩阵就是同一个线性变换在不同基下的矩阵表示
2.1.6 伴随与 Hermite 算子
伴随
设 A A A 是 Hilbert 空间 V V V 上的线性算子,实际上 V V V 上存在唯一的线性算子 A † A^{\dagger} A†,使得对所有向量 ∣ v ⟩ ∣ w ⟩ ∈ V \ket v \ket w \in V ∣v⟩∣w⟩∈V 成立:
( ∣ v ⟩ , A ∣ w ⟩ ) = ( A † ∣ v ⟩ , ∣ w ⟩ ) (\ket v, A \ket w) = (A^{\dagger}\ket v,\ket w) (∣v⟩,A∣w⟩)=(A†∣v⟩,∣w⟩)
即 ⟨ v ∣ A † w ⟩ = ⟨ A v ∣ w ⟩ = ⟨ w ∣ A v ⟩ ∗ \braket{v|A^{\dagger}w} = \braket{Av|w} = \braket{w|Av}^* ⟨v∣A†w⟩=⟨Av∣w⟩=⟨w∣Av⟩∗
这个线性算子称为 A A A 的伴随(adjoint)或 Hermite 共轭。如果 ∣ v ⟩ \ket v ∣v⟩ 是向量,则定义 ∣ v ⟩ † = ⟨ v ∣ \ket v ^{\dagger} = \bra v ∣v⟩†=⟨v∣.
性质:
- ( A B ) † = B † A † (AB)^{\dagger} = B^{\dagger}A^{\dagger} (AB)†=B†A† (从定义出发证明)
- ( ∣ w ⟩ ⟨ v ∣ ) † = ∣ v ⟩ ⟨ w ∣ (\ket w \bra v)^{\dagger} = \ket v \bra w (∣w⟩⟨v∣)†=∣v⟩⟨w∣ (用矩阵表示出来,Hermite 共轭运算的作用将矩阵变为共轭转置矩阵,即 A † = ( A ∗ ) T A^{\dagger} = (A^*)^T A†=(A∗)T)
- ( A ∣ v ⟩ ) † = ⟨ v ∣ † A † (A \ket v)^{\dagger} = \bra v^{\dagger} A^{\dagger} (A∣v⟩)†=⟨v∣†A†
- ( ∑ i a i A i ) † = ∑ i a i ∗ A i † (\sum_i a_iA_i)^{\dagger} = \sum_i a_i^* A_i^{\dagger} (∑iaiAi)†=∑iai∗Ai† (伴随的反线性)
- ( A † ) † = A (A^{\dagger})^{\dagger} = A (A†)†=A
厄密(自伴)算符:
如果 A † = A A^{\dagger} =A A†=A,即 ⟨ α ∣ A β ⟩ = ⟨ A α ∣ β ⟩ = ⟨ β ∣ A α ⟩ ∗ \braket{\alpha|A\beta} = \braket{A\alpha|\beta} = \braket{\beta|A\alpha}^* ⟨α∣Aβ⟩=⟨Aα∣β⟩=⟨β∣Aα⟩∗,则称 A A A 为 Hermite 或自伴算子。
从而 ⟨ α ∣ A α ⟩ = ⟨ A α ∣ α ⟩ = ⟨ α ∣ A α ⟩ ∗ \braket{\alpha|A\alpha} = \braket{A\alpha|\alpha} = \braket{\alpha|A\alpha}^* ⟨α∣Aα⟩=⟨Aα∣α⟩=⟨α∣Aα⟩∗,因此 ⟨ α ∣ A α ⟩ \braket{\alpha|A\alpha} ⟨α∣Aα⟩ 是实数。
也因此厄密算符 A A A 的对角元 A i i = ⟨ r i ∣ A r i ⟩ A_{ii} = \braket{r_i|Ar_i} Aii=⟨ri∣Ari⟩ 为实数。
⟨ r i ∣ A r j ⟩ = ⟨ A r i ∣ r j ⟩ = ⟨ r j ∣ A r i ⟩ ∗ \braket{r_i|Ar_j} = \braket{Ar_i|r_j}=\braket{r_j|Ar_i}^* ⟨ri∣Arj⟩=⟨Ari∣rj⟩=⟨rj∣Ari⟩∗,因此 A i j = A j i ∗ A_{ij} = A_{ji}^* Aij=Aji∗
投影算子
设 W W W 是 d d d 维向量空间 V V V 的 k k k 维算子,采用 Gram-Schimdt 过程,可以为 V V V 构造一个标准正交基 ∣ 1 ⟩ , . . . , ∣ d ⟩ \ket 1,...,\ket d ∣1⟩,...,∣d⟩, 使得 ∣ 1 ⟩ , . . . ∣ k ⟩ \ket 1,...\ket k ∣1⟩,...∣k⟩ 是 W W W 的一个标准正交基,定义
P = ∑ i k ∣ i ⟩ ⟨ i ∣ P = \sum_i^{k} \ket i \bra i P=i∑k∣i⟩⟨i∣
是 W W W 上的投影算子。
对任意向量 ∣ v ⟩ \ket v ∣v⟩, ∣ v ⟩ ⟨ v ∣ \ket v \bra v ∣v⟩⟨v∣ 都是厄密的,因此 P P P 也是厄密的,即 P † = P P^{\dagger} = P P†=P.
由完备性关系得, ∑ i ∣ i ⟩ ⟨ i ∣ = I \sum_i \ket i \bra i = I ∑i∣i⟩⟨i∣=I,因此 Q = I − P Q = I - P Q=I−P 为 P P P 的正交补.
对任意投影 P P P 满足 P 2 = P P^2 = P P2=P.
证明:
令 P = ∑ i ∣ i ⟩ ⟨ i ∣ P = \sum_i \ket i \bra i P=∑i∣i⟩⟨i∣,则 P 2 = ∑ i j ∣ i ⟩ ⟨ i ∣ j ⟩ ⟨ j ∣ = ∑ i j δ i j ⟨ i ∣ j ⟩ = ∑ i ∣ i ⟩ ⟨ i ∣ = P P^2 = \sum_{ij}\ket i \braket {i | j} \bra j = \sum_{ij} \delta_{ij}\braket{i|j} = \sum_i \ket i \bra i = P P2=∑ij∣i⟩⟨i∣j⟩⟨j∣=∑ijδij⟨i∣j⟩=∑i∣i⟩⟨i∣=P.
正规算子
算子 A A A 称为正规的,如果 A A † = A † A AA^{\dagger} = A^{\dagger}A AA†=A†A 成立。
性质:
- 正规矩阵是厄密的,当且仅当它的特征值为实数。
谱分解定理
一个算子是正规算子当且仅当它可对角化。
任意正规矩阵都可在经过一个酉变换后变为对角矩阵,反过来所有可在经过一个酉变换后变为对角矩阵的矩阵都是正规矩阵。
酉矩阵
满足 U U † = U † U = I UU^{\dagger} = U^{\dagger}U = I UU†=U†U=I。
-
U − 1 = U † U^{-1} = U^{\dagger} U−1=U†,且 U † U^{\dagger} U† 也是幺正算符
-
U U U 是正规的且有谱分解。
-
幺正算符的乘积也是幺正:
( U V ) ( U V ) † = U V V † U † = I (UV)(UV)^{\dagger} = UVV^{\dagger}U^{\dagger} = I (UV)(UV)†=UVV†U†=I
-
幺正算符保持两个算符内积不变:
⟨ U α ∣ U β ⟩ = ⟨ α ∣ U † U β ⟩ = ⟨ α ∣ β ⟩ \braket{U\alpha|U\beta} = \braket{\alpha|U^{\dagger}U\beta} = \braket{\alpha | \beta} ⟨Uα∣Uβ⟩=⟨α∣U†Uβ⟩=⟨α∣β⟩
-
幺正算符是正交矩阵(比如空间中的转动)的推广。相互正交的向量作相同转动后仍然正交。
-
∣ ψ ( t ) ⟩ = U ( t ) ∣ ψ ( 0 ) ⟩ \ket{\psi(t)} = U(t)\ket{\psi(0)} ∣ψ(t)⟩=U(t)∣ψ(0)⟩ 中的演化算符 U ( t ) U(t) U(t) 是幺正的。
谱分解定理证明
2.1.7 张量积
张量积是将向量空间合在一起,构成更大向量空间的一种方法。
设 V V V 和 W W W 是维数分别是 m m m 和 n n n 的向量空间,并假定 V V V 和 W W W 是 Hilbert 空间,于是 V ⊗ W V \otimes W V⊗W 是一个 m n mn mn 维向量空间。 V ⊗ W V \otimes W V⊗W 的元素是 V V V 的元素 ∣ v ⟩ \ket v ∣v⟩ 和 W W W 的元素 ∣ w ⟩ \ket w ∣w⟩ 的张量积 ∣ v ⟩ ⊗ ∣ w ⟩ \ket v \otimes \ket w ∣v⟩⊗∣w⟩ 的线性组合。如果 ∣ i ⟩ \ket i ∣i⟩ 和 ∣ j ⟩ \ket j ∣j⟩ 是 V V V 和 W W W 的标准正交基,则 ∣ i ⟩ ⊗ ∣ j ⟩ \ket i \otimes \ket j ∣i⟩⊗∣j⟩ 是 V ⊗ W V\otimes W V⊗W 的一个基。
性质:
- 对任意标量 z z z, V V V 的元素 v v v 和 W W W 的元素 w w w,满足 z ( ∣ v ⟩ ⊗ ∣ w ⟩ ) = ( z ∣ v ⟩ ) ⊗ ∣ w ⟩ = ∣ v ⟩ ⊗ ( z ∣ w ⟩ ) z(\ket v \otimes \ket w) = (z\ket v) \otimes \ket w = \ket v \otimes (z\ket w) z(∣v⟩⊗∣w⟩)=(z∣v⟩)⊗∣w⟩=∣v⟩⊗(z∣w⟩).
- 对 V V V 中任意的 v 1 v_1 v1 和 v 2 v_2 v2 和 W W W 中的 ∣ w ⟩ \ket w ∣w⟩,满足 ( ∣ v 1 ⟩ + ∣ v 2 ⟩ ) ⊗ ∣ w ⟩ = ∣ v 1 ⟩ ⊗ ∣ w ⟩ + ∣ v 2 ⟩ ⊗ ∣ w ⟩ (\ket {v_1} + \ket {v_2}) \otimes \ket w = \ket {v_1} \otimes \ket w + \ket {v_2} \otimes \ket w (∣v1⟩+∣v2⟩)⊗∣w⟩=∣v1⟩⊗∣w⟩+∣v2⟩⊗∣w⟩.
- 对 V V V 中任意的 ∣ v ⟩ \ket v ∣v⟩ 和 W W W 中的 w 1 w_1 w1 和 w 2 w_2 w2,满足 ∣ v ⟩ ⊗ ( ∣ w 1 ⟩ + ∣ w 2 ⟩ ) = ∣ v ⟩ ⊗ ∣ w 1 ⟩ + ∣ v ⟩ ⊗ ∣ w 2 ⟩ \ket v \otimes (\ket {w_1} + \ket {w_2}) = \ket v \otimes \ket {w_1} + \ket v \otimes \ket {w_2} ∣v⟩⊗(∣w1⟩+∣w2⟩)=∣v⟩⊗∣w1⟩+∣v⟩⊗∣w2⟩.
矩阵表示
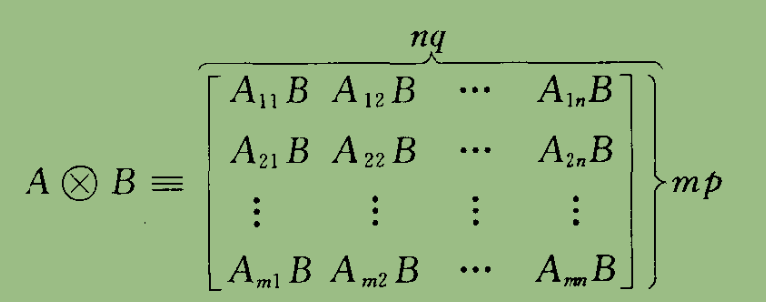
2.1.8 算子函数
定义
T r ( A ) = ∑ i = 1 n A i i Tr(A) = \sum_{i=1}^nA_{ii} Tr(A)=i=1∑nAii
如果有一组正交单位特征基 { ∣ i ⟩ } \{\ket i\} {∣i⟩},则存在 T r ( A ) = ∑ i ⟨ i ∣ A ∣ i ⟩ Tr(A) = \sum_i \bra i A \ket i Tr(A)=∑i⟨i∣A∣i⟩.
性质
-
T r ( A + B ) = T r ( A ) + T r ( B ) Tr(A+B) = Tr(A) + Tr(B) Tr(A+B)=Tr(A)+Tr(B)
-
T r ( c A ) = c T r ( A ) Tr(cA) = cTr(A) Tr(cA)=cTr(A)
-
T r ( A B ) = T r ( B A ) Tr(AB) = Tr(BA) Tr(AB)=Tr(BA)
证明
T r ( A B ) = ∑ i ⟨ i ∣ A B ∣ i ⟩ = ∑ i k ⟨ i ∣ A ∣ k ⟩ ⟨ k ∣ B ∣ i ⟩ = ∑ i k ⟨ k ∣ B ∣ i ⟩ ⟨ i ∣ A ∣ k ⟩ = ∑ k ⟨ k ∣ B A ∣ k ⟩ = T r ( B A ) Tr(AB) = \sum_i \bra i A B \ket i = \sum_{ik} \bra i A \ket k \bra k B \ket i = \sum_{ik}\bra k B \ket i \bra i A \ket k = \sum_k \bra k BA \ket k = Tr(BA) Tr(AB)=∑i⟨i∣AB∣i⟩=∑ik⟨i∣A∣k⟩⟨k∣B∣i⟩=∑ik⟨k∣B∣i⟩⟨i∣A∣k⟩=∑k⟨k∣BA∣k⟩=Tr(BA)
-
T r ( A 1 A 2 . . . A n ) = T r ( A 2 A 3 . . . A n A 1 ) = . . . = T r ( A n A 1 . . . A n − 1 ) Tr(A_1A_2...A_n) = Tr(A_2A_3...A_nA_1) = ... = Tr(A_nA_1...A_{n-1}) Tr(A1A2...An)=Tr(A2A3...AnA1)=...=Tr(AnA1...An−1)
迹与表象选择无关:选取 { ∣ i ⟩ } \{\ket i\} {∣i⟩} 和 { ∣ j ⟩ } \{\ket j\} {∣j⟩} 两组基, ∑ i ⟨ i ∣ A ∣ i ⟩ = ∑ i j ⟨ i ∣ j ⟩ ⟨ j ∣ A ∣ i ⟩ = ∑ i j ⟨ j ∣ A ∣ i ⟩ ⟨ i ∣ j ⟩ = ∑ j ⟨ j ∣ A ∣ j ⟩ \sum_i \bra{i} A \ket i = \sum_{ij}\braket {i|j} \bra j A \ket i = \sum_{ij} \bra j A \ket i \braket {i|j} = \sum_j \bra j A \ket j ∑i⟨i∣A∣i⟩=∑ij⟨i∣j⟩⟨j∣A∣i⟩=∑ij⟨j∣A∣i⟩⟨i∣j⟩=∑j⟨j∣A∣j⟩.
任何幺正算符 U U U:
T r ( U † A U ) = T r ( U U † A ) = T r ( A ) Tr(U^{\dagger}AU) = Tr(UU^{\dagger}A) = Tr(A) Tr(U†AU)=Tr(UU†A)=Tr(A)
算符期望值可写成迹:
T r ( A ∣ α ⟩ ⟨ α ∣ ) = ∑ i ⟨ i ∣ A ∣ α ⟩ ⟨ α ∣ i ⟩ = ∑ i ⟨ α ∣ i ⟩ ⟨ i ∣ A ∣ α ⟩ = ⟨ α ∣ A ∣ α ⟩ Tr(A\ket \alpha \bra \alpha) = \sum_i \bra i A \ket \alpha \braket {\alpha|i} = \sum_i \braket{\alpha|i}\bra i A \ket \alpha = \bra \alpha A \ket \alpha Tr(A∣α⟩⟨α∣)=i∑⟨i∣A∣α⟩⟨α∣i⟩=i∑⟨α∣i⟩⟨i∣A∣α⟩=⟨α∣A∣α⟩
∣ ψ ⟩ \ket \psi ∣ψ⟩ 扩展成一个以 ψ \psi ψ 为首个元的标准正交基 ∣ i ⟩ \ket i ∣i⟩,因此 ⟨ α ∣ i ⟩ = δ α i \braket {\alpha|i} = \delta_{\alpha i} ⟨α∣i⟩=δαi.
2.1.9 对易式和反对易式
两个算子 A A A 和 B B B 之间的对易式定义为 [ A , B ] = A B − B A [A,B]=AB-BA [A,B]=AB−BA.
若 A B = B A AB = BA AB=BA,则说明 A A A 和 B B B 是对易的。
两个算子 A A A 和 B B B 的反对易式定义为 { A , B } = A B + B A \{A,B\} = AB + BA {A,B}=AB+BA.
若 { A , B } = 0 \{A,B\} = 0 {A,B}=0,则说明 A A A 和 B B B 反对易。
同时对角化定理
设 A A A 和 B B B 是厄密算子,当且仅当存在一个标准正交基,使 A A A 和 B B B 在这个基下同时是对角的,则 [ A , B ] = 0 [A,B] = 0 [A,B]=0.在这种情况下, A A A 和 B B B 称为可同时对角化。
Gram-Schmidt正交化(构造正交归一基)
考虑完备集 { ∣ α 1 ⟩ , ∣ α 2 ⟩ , . . . , ∣ α n ⟩ } \{\ket{\alpha_1},\ket{\alpha_2},...,\ket{\alpha_n}\} {∣α1⟩,∣α2⟩,...,∣αn⟩}.
∣ β 1 ⟩ = ∣ α 1 ⟩ \ket{\beta_1} = \ket{\alpha_1} ∣β1⟩=∣α1⟩.
∣ β i ⟩ = ∣ α i ⟩ − P 1... i − 1 ∣ α i ⟩ \ket{\beta_i} = \ket{\alpha_i} - P_{1...i-1}\ket{\alpha_i} ∣βi⟩=∣αi⟩−P1...i−1∣αi⟩ (从 α i \alpha_i αi 中去除其在 ∣ β 1 ⟩ , . . . , ∣ β i − 1 ⟩ \ket{\beta_1},...,\ket{\beta_{i-1}} ∣β1⟩,...,∣βi−1⟩ 上的分量)
其中 P 1... i − 1 = ∑ k = 1 i − 1 ∣ β ′ ⟩ ⟨ β ′ ∣ P_{1...i-1} = \sum_{k=1}^{i-1}\ket{\beta^{'}}\bra{\beta^{'}} P1...i−1=∑k=1i−1∣β′⟩⟨β′∣ 是 ∣ β 1 ′ ⟩ , . . . , ∣ β i − 1 ′ ⟩ \ket{\beta^{'}_1},...,\ket{\beta^{'}_{i-1}} ∣β1′⟩,...,∣βi−1′⟩ 张成的子空间的投影算符。
可以得到 ∣ β i ⟩ = ∣ α i ⟩ − ∑ k = 1 i − 1 ⟨ β k ∣ α i ⟩ ⟨ β k ∣ β k ⟩ ∣ β k ⟩ \ket{\beta_i} = \ket{\alpha_i} - \sum_{k=1}^{i-1}\frac{\braket{\beta_k|\alpha_i}}{\braket{\beta_k|\beta_k}}\ket{\beta_k} ∣βi⟩=∣αi⟩−∑k=1i−1⟨βk∣βk⟩⟨βk∣αi⟩∣βk⟩
β ′ = ∣ β i ⟩ ∣ ∣ ∣ β i ⟩ ∣ ∣ , i = 1 , 2 , . . . , n \beta^{'} = \frac{\ket{\beta_i}}{||\ket{\beta_i}||}, i=1,2,...,n β′=∣∣∣βi⟩∣∣∣βi⟩,i=1,2,...,n 正交归一基。
完备性关系
已知 α i \alpha_i αi 是 ∣ α ⟩ \ket{\alpha} ∣α⟩ 的基向量, a i = ⟨ α i ∣ α ⟩ a_i = \braket{\alpha_i|\alpha} ai=⟨αi∣α⟩, ∑ i ∣ α i ⟩ ⟨ α i ∣ = I \sum_i \ket{\alpha_i}\bra{\alpha_i} = I ∑i∣αi⟩⟨αi∣=I.
证明: ( ∑ i ∣ α i ⟩ ⟨ α i ∣ ) ∣ α ⟩ = ∑ i ∣ α i ⟩ ⟨ α i ∣ α ⟩ = ∑ i a i ∣ α i ⟩ = ∣ α ⟩ (\sum_i \ket{\alpha_i}\bra{\alpha_i})\ \ket{\alpha} = \sum_i\ket{\alpha_i}\braket{\alpha_i|\alpha} = \sum_i a_i \ket{\alpha_i} = \ket{\alpha} (∑i∣αi⟩⟨αi∣) ∣α⟩=∑i∣αi⟩⟨αi∣α⟩=∑iai∣αi⟩=∣α⟩,因此 ∑ i ∣ α i ⟩ ⟨ α i ∣ = I \sum_i \ket{\alpha_i}\bra{\alpha_i} = I ∑i∣αi⟩⟨αi∣=I.
相关文章:
[量子计算与量子信息] 2.1 线性代数
2.1 线性代数 符号对照表 量子力学中,向量使用 ∣ ψ ⟩ \ket \psi ∣ψ⟩ (ket)来表示,可以理解为一个列向量。其对偶向量为 ⟨ ψ ∣ \bra \psi ⟨ψ∣ ,可以理解为行向量。 向量空间中零向量直接用 0 0 0 表示, ∣ 0 ⟩ \…...
【PG】PostgreSQL 目录结构
目录 1 软件安装目录 2 数据文件目录 base/:存储每个数据库的基本数据文件 global/:包含了全局性质的系统表空间文件 pg_tblspc/:包含了表空间的符号链接 pg_twophase/:包含了两阶段提交中使用的文件 pg_stat_tmp/ÿ…...

H5游戏源码分享-超级染色体小游戏
H5游戏源码分享-超级染色体小游戏 游戏玩法 不断地扩大发展同颜色的色块 用最少的步数完成游戏 <!DOCTYPE html> <html><head><meta charset"UTF-8"><meta name"viewport"content"widthdevice-width,user-scalableno,init…...
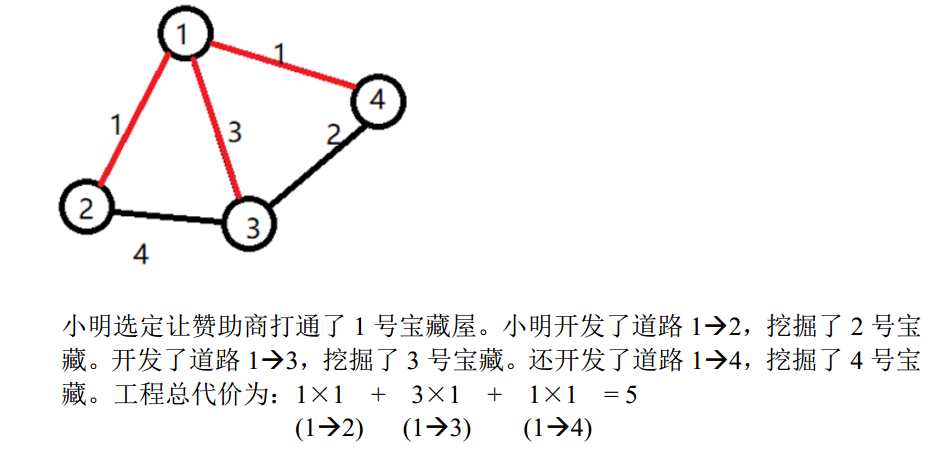
NOIP 2017 宝藏----Java题解
目录 NOIP 2017 宝藏 题目描述 输入描述: 输出描述: 输入 输出 说明 输入 输出 说明 备注: 代码实现: NOIP 2017 宝藏 时间限制:C/C 1秒,其他语言2秒 空间限制:C/C 262144K,其他语言524288K 64bit IO For…...

数据结构和算法的重要性
目录 1.什么是数据结构? 2.什么是算法? 3.数据结构和算法的重要性 4.如何学好数据结构和算法 1.什么是数据结构? 数据结构(Data Structure)是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合 …...

2023.11.10 信息学日志
2023.11.10 信息学日志 1. CF1613E Crazy Robot题目描述题目概况思路点拨 1. CF1613E Crazy Robot 题目描述 https://www.luogu.com.cn/problem/CF1613E 题目概况 来源:Codeforces 洛谷难度: 绿题 \color{green}绿题 绿题 CF难度: 2000…...
0基础学习VR全景平台篇第120篇:极坐标处理接缝 - PS教程
上课!全体起立~ 大家好,欢迎观看蛙色官方系列全景摄影课程! 紧跟上节课,我们已经学会了怎么利用PS蒙版工具来对航拍全景图补天。但是在后续工作学习中,我们会遇到天空这部分存在部分接缝的问题,如图&…...
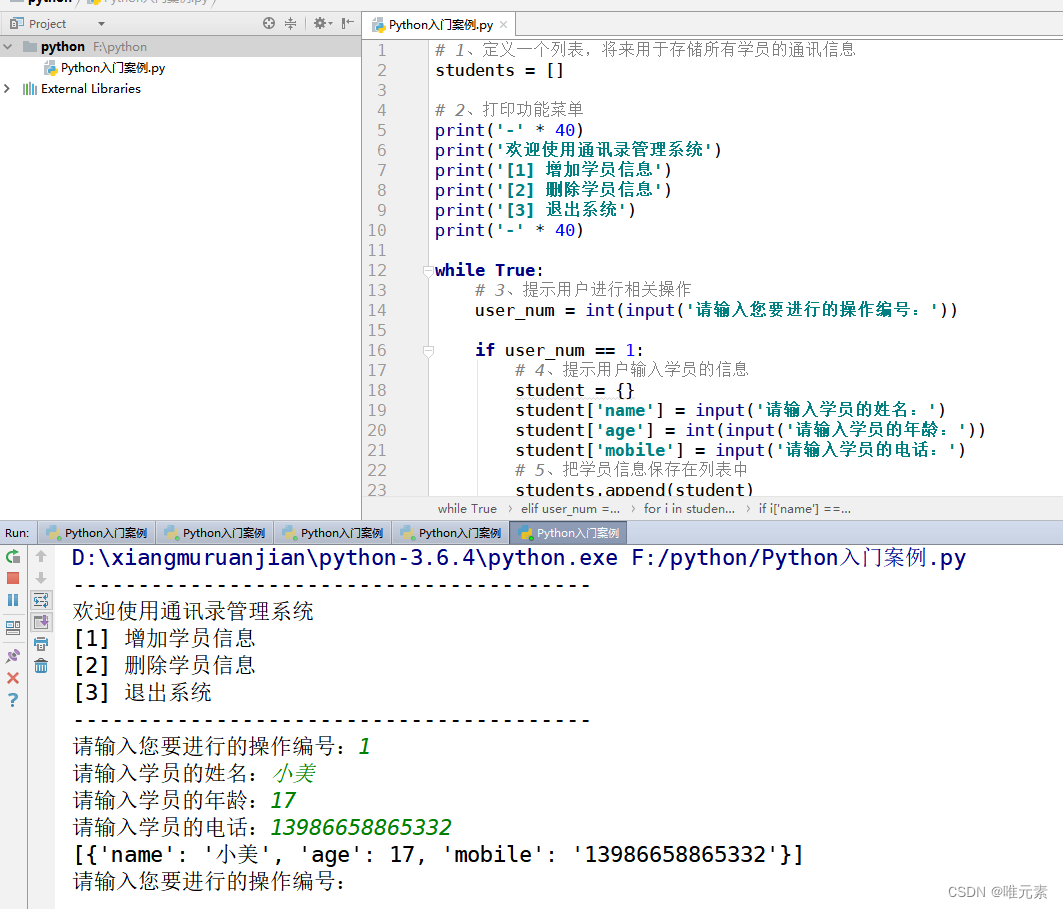
Python---综合案例:通讯录管理系统---涉及点:列表、字典、死循环
需求: 开个一个通讯录的管理系统,主要用于实现存储班级中同学的信息(姓名、年龄、电话) 涉及点:列表、字典、死循环 相关链接:Python--列表及其应用场景---增、删、改、查。-CSDN博客 Python---字典---…...

Vite探索:构建、启程、原理、CSS艺术与插件魔法
文章目录 1 构建工具1.1 什么是构建工具1.2 主流构建工具1.3 vite相较于webpack的优势 2 vite启动项目初体验2.1 你必须要理解的vite脚手架和vite2.2 vite开箱即用2.3 vite的预加载2.4 vite配置文件处理细节2.5 vue环境变量配置 3 vite 原理篇3.1 vite是怎么让浏览器可以识别.v…...

网工内推 | 网工校招,金融、软件行业,HCIE认证优先,最高15薪
01 长威信息科技 招聘岗位:网络工程师(24届校招) 职责描述: 1、负责网络类、安全类产品的安装部署、调试和运行维护,以及网络故障分析、定位和处理; 2、负责实施项目各类文档编制工作,包括技术…...
CVE-2023-25194 Kafka JNDI 注入分析
Apache Kafka Clients Jndi Injection 漏洞描述 Apache Kafka 是一个分布式数据流处理平台,可以实时发布、订阅、存储和处理数据流。Kafka Connect 是一种用于在 kafka 和其他系统之间可扩展、可靠的流式传输数据的工具。攻击者可以利用基于 SASL JAAS 配置和 SASL …...
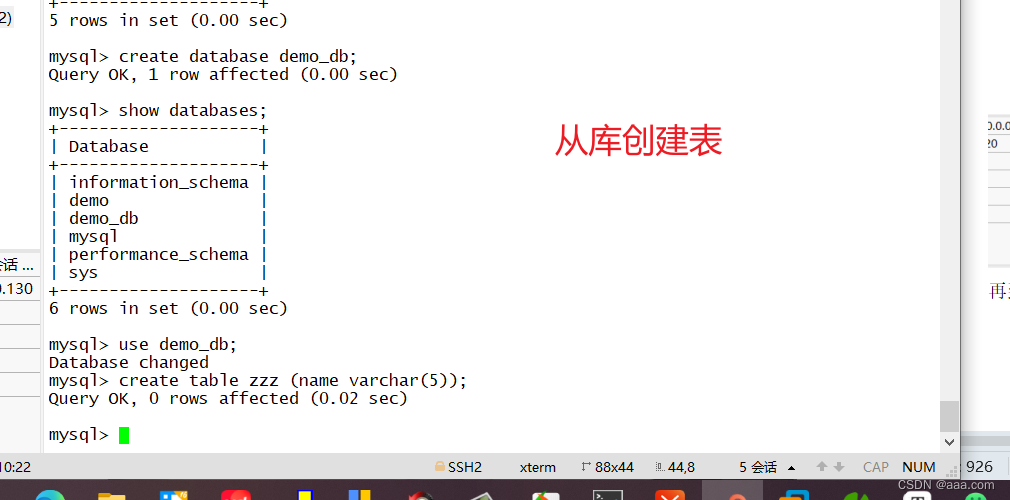
MySQL--主从复制和读写分离
MySQL主从复制和读写分离相关知识 1.什么是读写分离 读写分离,基本的原理是让主数据库处理事务性增、改、删操作( INSERT、UPDATE、DELETE) ,而从数据库处理SELECT查询操作。数据库复制被用来把事务性操作导致的变更同步到集群中的从数据库。 2.为什么要…...

JavaScript使用webcomponent的简单示例
官方网站: Web Component - Web API 接口参考 | MDN 1. 给一个html文件的路径字符串path, 存储对应path下的template,script,style数据 1) 传入path 2) 使用fetch将path字符串所在的文件找到并返回内容 const res await fetch(path).then(res > res.text()); 3) 使用…...
LeetCode(10)跳跃游戏 II【数组/字符串】【中等】
目录 1.题目2.答案3.提交结果截图 链接: 45. 跳跃游戏 II 1.题目 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nu…...

浅谈数据结构之递归
1. 递归的定义 递归是一种在解决问题时使用自身的特殊方法。在计算机科学和数据结构中,递归是一种通过将问题分解成更小的、相似的子问题来解决复杂问题的方法。递归可以直接或间接地调用自身,将大问题转化为规模较小的子问题,直到达到基本情…...

在CentOS7环境下安装Mysql
1.卸载已有的不需要的环境 使用如下命令,查看系统中是否已经存在mysql和mariadb(mysql的一个子分支) ps ajx | grep mariadb ps ajx | grep mysql 如果显示与我相同,则代表系统中已经存在这些环境并且已经停止 如果不相同则需要…...
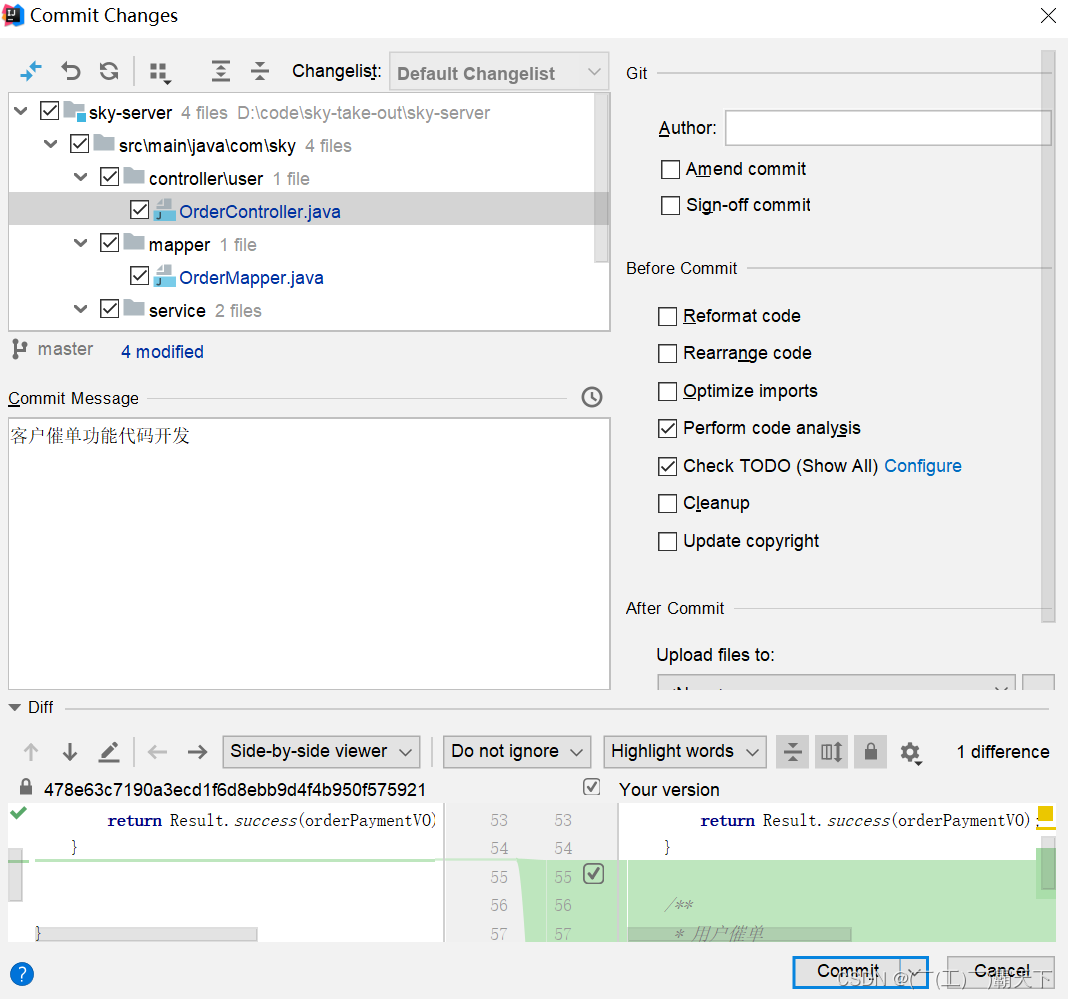
苍穹外卖-day10
苍穹外卖-day10 课程内容 Spring Task订单状态定时处理WebSocket来单提醒客户催单 功能实现:订单状态定时处理、来单提醒和客户催单 订单状态定时处理: 来单提醒: 客户催单: 1. Spring Task 1.1 介绍 Spring Task 是Spring框…...

牛客网刷题笔记131111 Python实现LRU+二叉树先中后序打印+SQL并列排序
从学校步入职场一年多,已经很久没刷过题了,为后续稍微做些提前的准备,还是重新开始刷刷题。 从未做过计划表,这回倒是做了个计划表,希望能坚持吧。 刷题比较随性且量级不大,今天就写了2个算法2个sql&#x…...
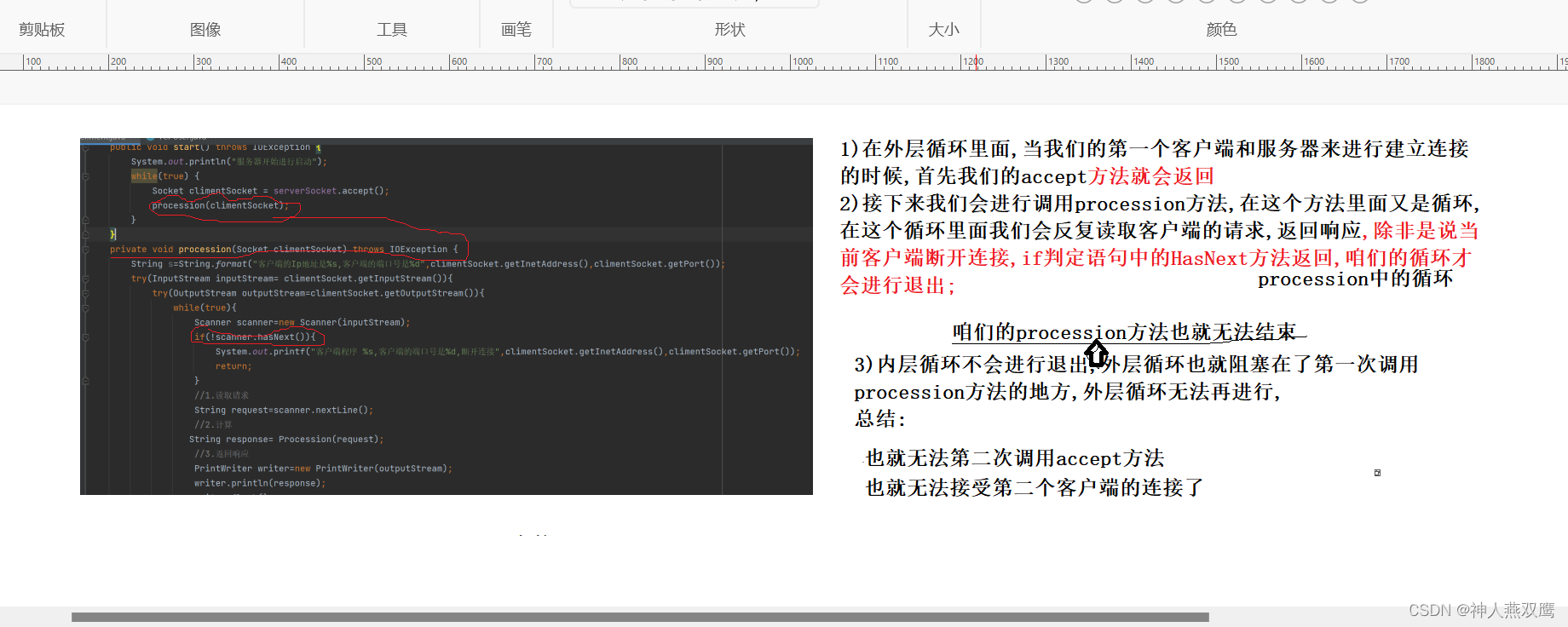
TCP网络编程
一)TCP Socket介绍: 1)TCP和UDP有着很大的不同,TCP想要进行网络通信的话首先需要通信双方建立连接以后然后才可以进行通信,TCP进行网络编程的方式和文件中的读写字节流类似,是以字节为单位的流进行传输 2)针对于TCP的套接字来说,J…...
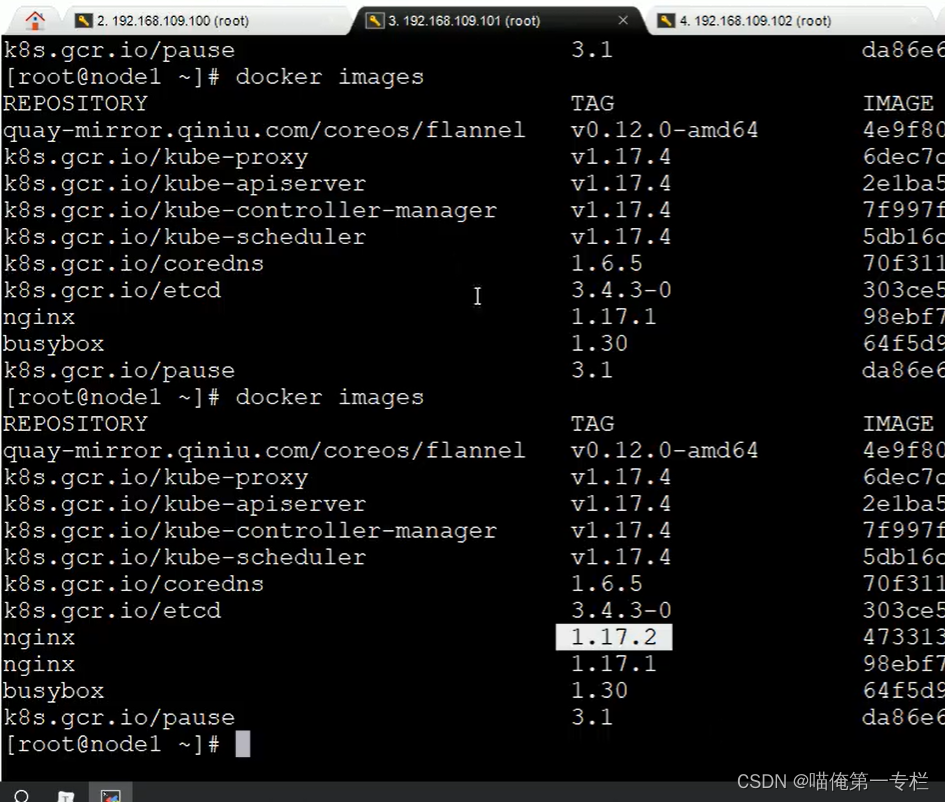
K8S知识点(九)
(1)Pod详解-结构和定义 一级属性有下面这些:前两个属性是字符串,上面有定义 kind:Pod version:v1 下面的属性是object 还可以继续查看子属性:二级属性 还可以继续查看三级属性: 通…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
