数据库系统原理与实践 笔记 #8
文章目录
- 数据库系统原理与实践 笔记 #8
- 关系数据库设计(续)
- 规范化(Normalization)
- 范式(Normal Form)
- 第一范式
- 第二范式
- Boyce-Codd范式(BCNF)
- 将模式分解成BCNF
- BCNF和保持依赖
- 第三范式
- 函数依赖理论
- 正则覆盖
- 无关属性
- 无关属性的验证
- 无损分解
- 保持依赖
数据库系统原理与实践 笔记 #8
关系数据库设计(续)
规范化(Normalization)
范式(Normal Form)
- 各种范式之间包含关系如下:
5 N F ⊂ 4 N F ⊂ B C N F ⊂ 3 N F ⊂ 2 N F ⊂ 1 N F 5NF\subset4NF\subset BCNF\subset3NF\subset2NF\subset1NF 5NF⊂4NF⊂BCNF⊂3NF⊂2NF⊂1NF - 某一关系模式R最高属于第n范式,可简记为 R ∈ n N F R\in nNF R∈nNF
第一范式
- 如果某个域的元素被认为是不可分的单元,那么这个域就是原子的,如果一个关系模式R的所有属性域都是原子的,我们称关系模式R属于第一范式
- 非原子的值会造成复杂存储及数据冗余
第二范式
- 定义:若关系模式 R ∈ 1 N F R\in 1NF R∈1NF,且在 F + F^+ F+中每一个非主属性完全函数依赖于候选码,则 R ∈ 2 N F R\in 2NF R∈2NF
Boyce-Codd范式(BCNF)
- 具有函数依赖集F的关系模式R属于BCNF的条件是:对所有 F + F^+ F+中形如 α → β \alpha\rightarrow\beta α→β的函数依赖( α ⊆ R \alpha\subseteq R α⊆R且 β ⊆ R \beta\subseteq R β⊆R),下面至少有一个成立:
- α → β \alpha\rightarrow\beta α→β是平凡的函数依赖(即 β ⊆ α \beta\subseteq\alpha β⊆α)
- α \alpha α是模式R的一个超码
- 另一个判断准则:在关系模式R(U,F)中,如果 F + F^+ F+ 中的每一个非平凡函数依赖的决定属性集都包含候选码,则 r ( R ) ∈ B C N F r(R)\in BCNF r(R)∈BCNF
- BCNF范式:排除了任何属性(包括主属性和非主属性)对候选码的部分依赖和传递依赖,也排除了主属性之间的传递依赖
将模式分解成BCNF
- 假设有模式R,及其一个非平凡依赖 α → β \alpha\rightarrow\beta α→β不属于BCNF,那么我们可以将R分解成: ( α ∪ β ) (\alpha\cup\beta) (α∪β)和 ( R − ( β − α ) ) (R-(\beta-\alpha)) (R−(β−α))
BCNF和保持依赖
- 检查包括各种约束(码、check子句、函数依赖、断言等)的开销是很大的,但是如果只涉及到单个关系,检查约束的开销相对较低
- 如果F上的每一个函数依赖都在其分解后的一个关系上成立,那么这个分解是保持依赖的
第三范式
- 具有函数依赖集F的关系模式R属于第三范式的条件是:对 F + F^+ F+ 中所有形如 α → β \alpha\rightarrow\beta α→β的函数依赖中,至少有以下之一成立:
- α → β \alpha\rightarrow\beta α→β是一个平凡的函数依赖(即 β ⊆ α \beta\subseteq\alpha β⊆α)
- α \alpha α是R的一个超码啊
- β − α \beta-\alpha β−α的每个属性A都包含在R的候选码中
- 第三个条件是BCNF的一个最小放宽:即允许存在主属性对候选码的传递依赖和部分依赖,在函数依赖集F中用来满足保持某些函数依赖
- 等价定义:
- 关系模式R(U,F)中,若不存在这样的码X、属性组Y及非主属性Z( Z ⊈ Y Z\nsubseteq Y Z⊈Y),使得 X → Y ( Y ↛ X ) , Y → Z X\rightarrow Y(Y\nrightarrow X),Y\rightarrow Z X→Y(Y↛X),Y→Z,则称R(U,F) ∈ \in ∈ 3NF
- 具有函数依赖集F的关系模式R属于3NF,则R中任何非主属性A既不部分依赖于码也不传递依赖于R的码
函数依赖理论
正则覆盖
- 函数依赖集可能存在冗余依赖(这些依赖可以从其他依赖中推导出来)
- 直观上,F的正则覆盖 F c F_c Fc没有任何冗余依赖或存在冗余部分的依赖
- F c F_c Fc具有和F相同的函数依赖集闭包。其意义在于:验证 F c F_c Fc比验证F更容易,3NF算法必备
无关属性
- 如果去除函数依赖中的一个属性不改变该函数依赖集的必报,则称该属性是无关属性
- 形式化定义:考虑函数依赖集 F F F及其 F F F中函数依赖 α → β \alpha\rightarrow\beta α→β:
- 如果 A ∈ α A\in\alpha A∈α并且 F F F逻辑蕴含( F − { α → β } ∪ { ( α − A ) → β } F-\{\alpha\rightarrow\beta\}\cup\{(\alpha-A)\rightarrow\beta\} F−{α→β}∪{(α−A)→β}),则属性A在 α \alpha α中是无关的
- 如果 A ∈ β A\in\beta A∈β并且函数依赖集( F − { α → β } ∪ { α → ( β − A ) } F-\{\alpha\rightarrow\beta\}\cup\{\alpha\rightarrow(\beta-A)\} F−{α→β}∪{α→(β−A)})逻辑蕴含F,则属性A在 β \beta β中是无关的
无关属性的验证
- 验证方法:考虑函数依赖集F及F中的函数依赖 α → β \alpha\rightarrow\beta α→β,验证属性 A ∈ α A\in\alpha A∈α是不是多余的
无损分解
- 对于 R = ( R 1 , R 2 ) R=(R_1,R_2) R=(R1,R2),我们要求模式 R R R上的所有可能关系r都有 r = ∏ R 1 ( r ) ⋈ ∏ R 2 ( r ) r=\prod_{R_1}(r)\bowtie\prod_{R_2}(r) r=∏R1(r)⋈∏R2(r)
- 如果下面的依赖中至少有一个属于 F + F^+ F+,那么将R分解成 R 1 R_1 R1和 R 2 R_2 R2是无损分解连接:
- R 1 ∩ R 2 → R 1 R_1\cap R_2\rightarrow R_1 R1∩R2→R1
- R 1 ∩ R 2 → R 2 R_1\cap R_2\rightarrow R_2 R1∩R2→R2
- 即 R 1 ∩ R 2 R_1\cap R_2 R1∩R2是 R 1 R_1 R1或 R 2 R_2 R2的超码
- 上述函数依赖测试只是无损连接的一个充分条件,只有当所有约束都是函数依赖时,它才是必要条件
保持依赖
- F为模式R上的一个函数依赖集, R 1 , R 2 , . . . , R n R_1,R_2,...,R_n R1,R2,...,Rn为R的一个分解,F在 R i R_i Ri上的限定是 F + F^+ F+中所有只包含 R i R_i Ri中属性的函数依赖的集合 F i F_i Fi
相关文章:

数据库系统原理与实践 笔记 #8
文章目录 数据库系统原理与实践 笔记 #8关系数据库设计(续)规范化(Normalization)范式(Normal Form)第一范式第二范式Boyce-Codd范式(BCNF)将模式分解成BCNFBCNF和保持依赖第三范式 函数依赖理论正则覆盖无关属性无关属性的验证无损分解保持依赖 数据库系统原理与实践 笔记 #8 …...

Ubuntu 和 Windows 文件互传
FTP 服务 FTP 采用 Internet 标准文件传输协议 FTP 的用户界面, 向用户提供了一组用来管理计算机之间文件传输的应用程序。在开发的过程中会频繁的在 Windows 和 Ubuntu 下进行文件传输,比如在 Windwos 下进行代码编写,然后将编写好的代码拿到…...

如何在WPF应用程序中全局捕获异常
在WPF (Windows Presentation Foundation) 应用程序中,你可以使用 AppDomain.CurrentDomain.UnhandledException 事件来全局捕获未处理的异常。这个事件会在应用程序中的任何地方发生未处理的异常时触发。以下是一个简单的例子,演示如何在WPF应用程序中全…...
自定义Matplotlib中的颜色映射(cmap)
要自定义Matplotlib中的颜色映射(cmap),您可以按照以下步骤进行操作: 导入所需的库: import numpy as np import matplotlib.pyplot as plt from matplotlib.colors import LinearSegmentedColormap创建自定义颜色映…...

Ansible的filter
环境 控制节点:Ubuntu 22.04Ansible 2.10.8管理节点:CentOS 8 filter 使用filter可以对数据做操作,比如把JSON数据转换为YAML数据,从URL中解析出hostname,提取字符串的SHA1哈希值,做数学运算,…...

Qt绘制各种图表
绘制柱状图: void MainWindow::iniBarChart() { //柱状图初始化QChart *chart new QChart(); //创建chartchart->setTitle("Barchart演示");chart->setAnimationOptions(QChart::SeriesAnimations);ui->chartViewBar->setChart(chart); //为…...

【科研新手指南4】ChatGPT的prompt技巧 心得
ChatGPT的prompt心得 写在最前面chatgpt咒语1(感觉最好用的竟然是这个,简单方便快捷,不需要多轮对话)chatgpt思维链2(复杂任务更适用,简单任务把他弄复杂了)机理chatgpt完整咒语1(感…...
龙蜥社区联合浪潮信息发布《eBPF技术实践白皮书》(附下载链接)
随着 eBPF 技术的高速发展,eBPF 已成为 Linux 内核顶级子系统,并扩展到内核网络、存储、内存、调度和安全等子模块。这种可编程底座内核框架构建了全系统,是云计算、运维和安全等领域技术创新的基础。 龙蜥社区在 eBPF 领域进行了广泛的实践…...

屏幕截图软件 Snagit mac中文版软件特点
Snagit mac是一款屏幕截图和视频录制软件,它可以帮助用户快速捕捉屏幕上的任何内容,并将其编辑、标注和共享。 Snagit mac软件特点 多种截图模式:支持全屏截图、窗口截图、区域截图、延时截图等多种截图模式,满足不同用户的需求。…...

四、Ribbon负载均衡
目录 一、负载均衡流程 1、我通过浏览器直接访问userservice/user/1,无法访问,说明是负载均衡做了相应的处理 2、我们来看一下代码中负载均衡的流程是怎样的 3、图像流程 二、负载均衡策略 1、修改负载均衡策略 (方式一) &a…...
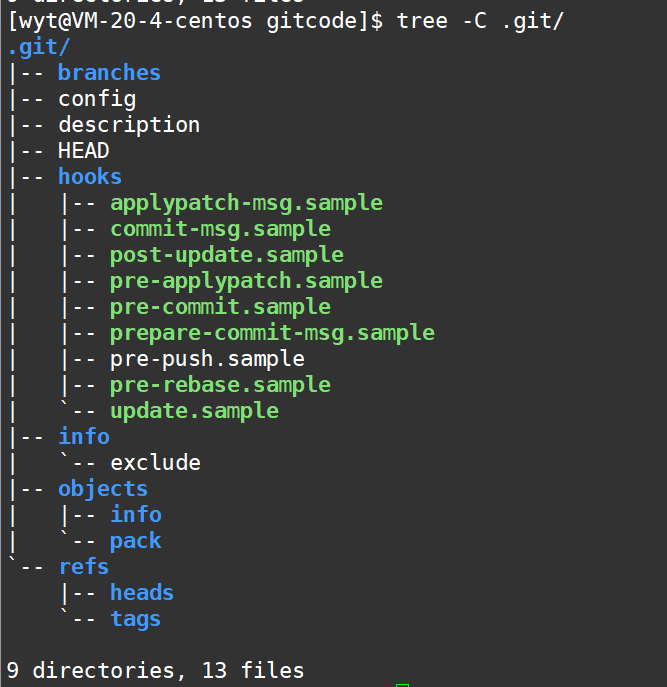
【Git】第二篇:基本操作(创建本地仓库)
我们知道,git是一个版本控制器,可以帮我们控制管理电脑上所有格式的文档。 而我们需要使用git管理文件的时候,我们必须将这些文件放到git仓库中,只有在git仓库中的文件才可以被我们的git追踪管理 创建本地仓库 创建本地仓库是需…...

vuex——重置vuex数据
需求描述 登出系统时,需将 vuex 中存储的数据,恢复为最初的默认状态。 实现方法 通过 replaceState 方法,将最初的 vuex 的 state 数据作为参数传入即可 完整代码范例 src\store\index.js import Vue from "vue"; import Vuex fro…...
)
WebSphere Liberty 8.5.5.9 (三)
WebSphere Liberty 8.5.5.9 将资源先下载,后期本地安装 下载 passwordUtilities-1.0 D:\wlp-webProfile7-java8-8.5.5.9\wlp\bin>installUtility find password 正在建立与已配置存储库的连接... 此过程可能要花几分钟完成。已成功连接至所有已配置的存储库。…...

如何区分一个项目是react还react native
要区分一个项目是 React 还是 React Native,你可以关注以下几个方面: 项目目录结构:React 和 React Native 项目通常具有不同的目录结构。React 项目中的源代码通常位于一个名为 "src" 或 "app" 的文件夹中,包…...

网易有道开源语音合成引擎“易魔声”
概述 11 月 10 日,网易有道正式上线“易魔声”开源语音合成(TTS)引擎,所有用户可免费在开源社区 GitHub 进行下载使用,通过其提供的 web 界面及批量生成结果的脚本接口,轻松实现音色的情感合成与应用。 据…...
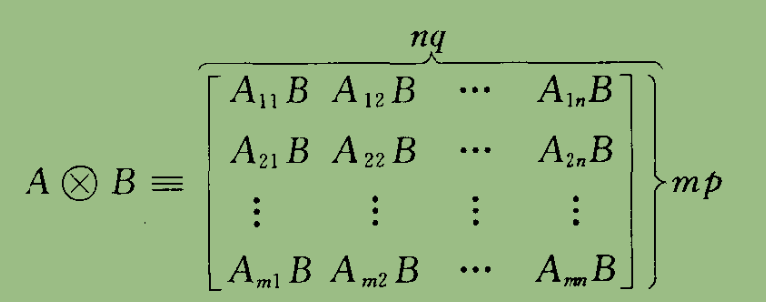
[量子计算与量子信息] 2.1 线性代数
2.1 线性代数 符号对照表 量子力学中,向量使用 ∣ ψ ⟩ \ket \psi ∣ψ⟩ (ket)来表示,可以理解为一个列向量。其对偶向量为 ⟨ ψ ∣ \bra \psi ⟨ψ∣ ,可以理解为行向量。 向量空间中零向量直接用 0 0 0 表示, ∣ 0 ⟩ \…...
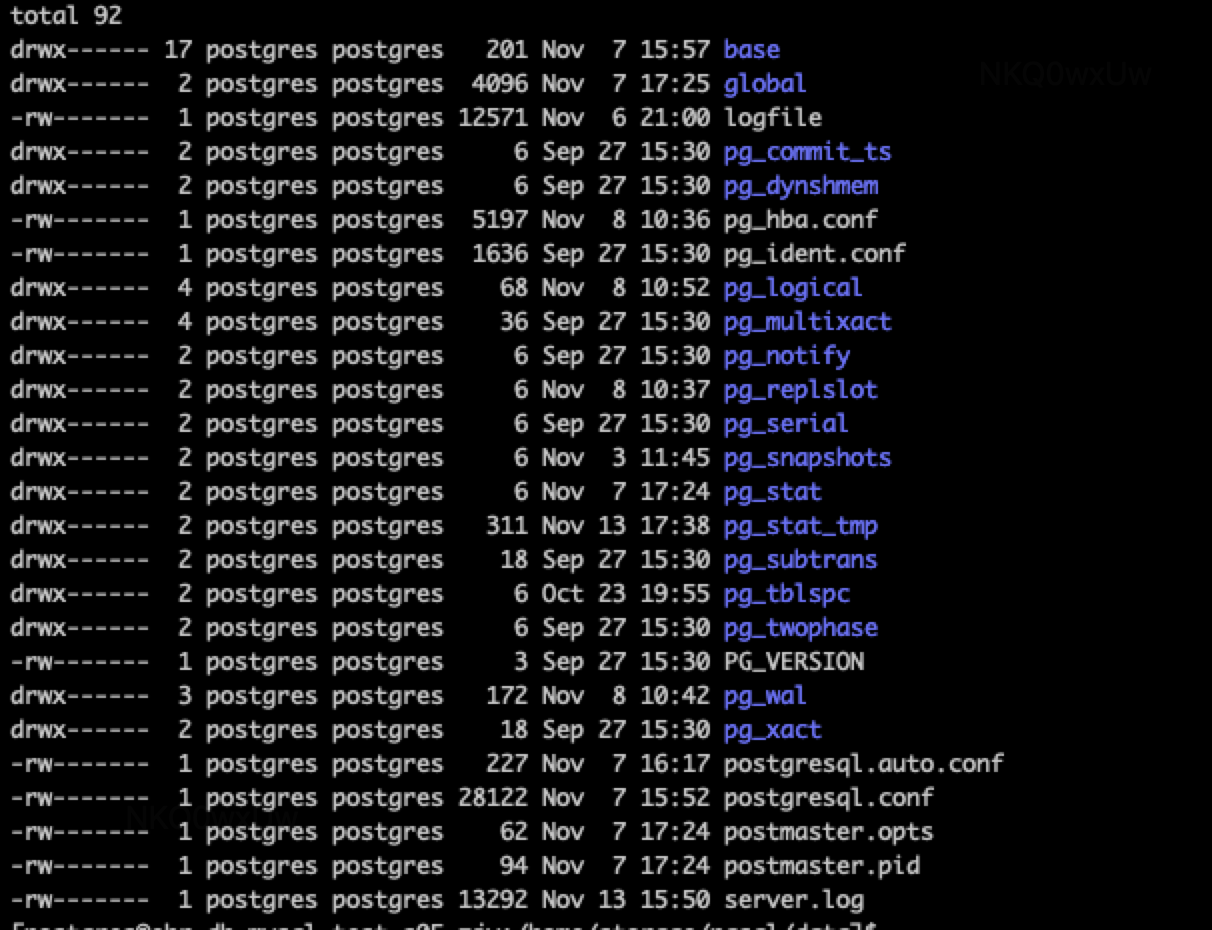
【PG】PostgreSQL 目录结构
目录 1 软件安装目录 2 数据文件目录 base/:存储每个数据库的基本数据文件 global/:包含了全局性质的系统表空间文件 pg_tblspc/:包含了表空间的符号链接 pg_twophase/:包含了两阶段提交中使用的文件 pg_stat_tmp/ÿ…...

H5游戏源码分享-超级染色体小游戏
H5游戏源码分享-超级染色体小游戏 游戏玩法 不断地扩大发展同颜色的色块 用最少的步数完成游戏 <!DOCTYPE html> <html><head><meta charset"UTF-8"><meta name"viewport"content"widthdevice-width,user-scalableno,init…...
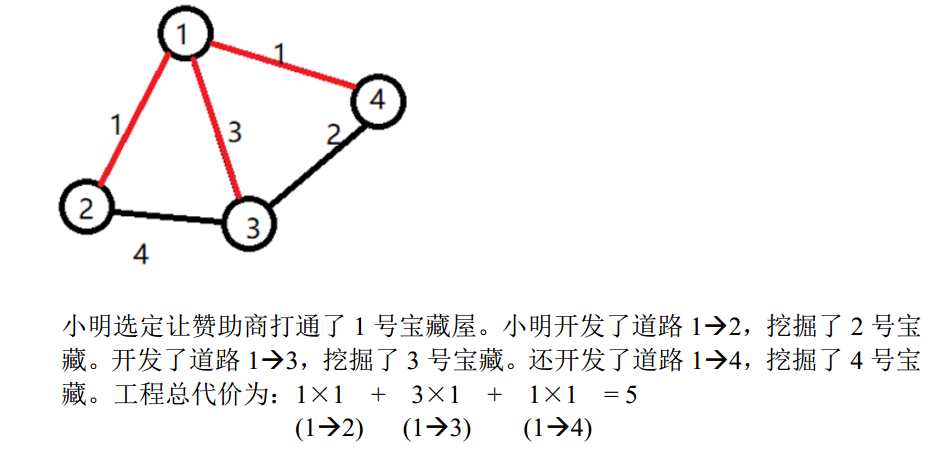
NOIP 2017 宝藏----Java题解
目录 NOIP 2017 宝藏 题目描述 输入描述: 输出描述: 输入 输出 说明 输入 输出 说明 备注: 代码实现: NOIP 2017 宝藏 时间限制:C/C 1秒,其他语言2秒 空间限制:C/C 262144K,其他语言524288K 64bit IO For…...

数据结构和算法的重要性
目录 1.什么是数据结构? 2.什么是算法? 3.数据结构和算法的重要性 4.如何学好数据结构和算法 1.什么是数据结构? 数据结构(Data Structure)是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合 …...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...
