647. 回文子串 516.最长回文子序列
647. 回文子串
题目:
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 2:
- 输入:"aaa"
- 输出:6
- 解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
dp数组的含义:
观察到不能之间用题目所求套上dp数组,看不出意义,那就看题目里有没有性质可以利用。这里用的是回文串的性质。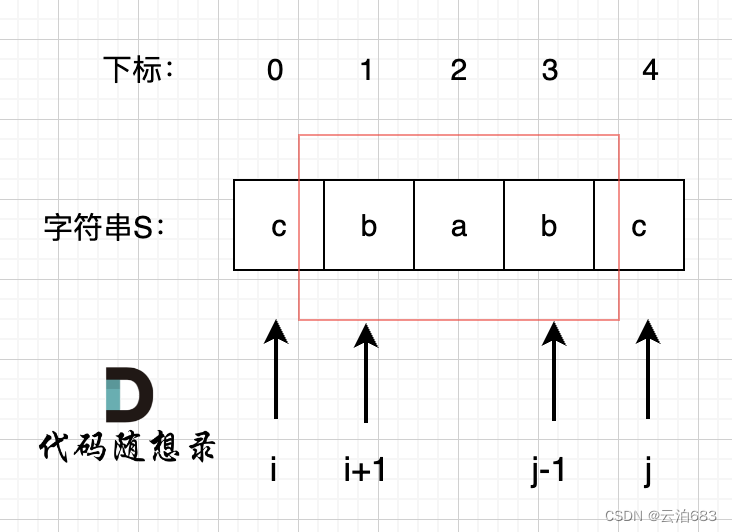
如果i+1到j-1是回文串,那么如果i和j的值相等,i到j也是回文串。
布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
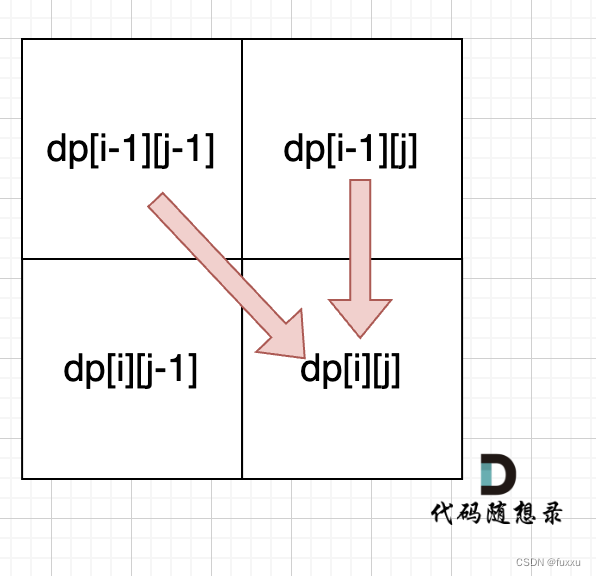
输入"aaa",dp图如下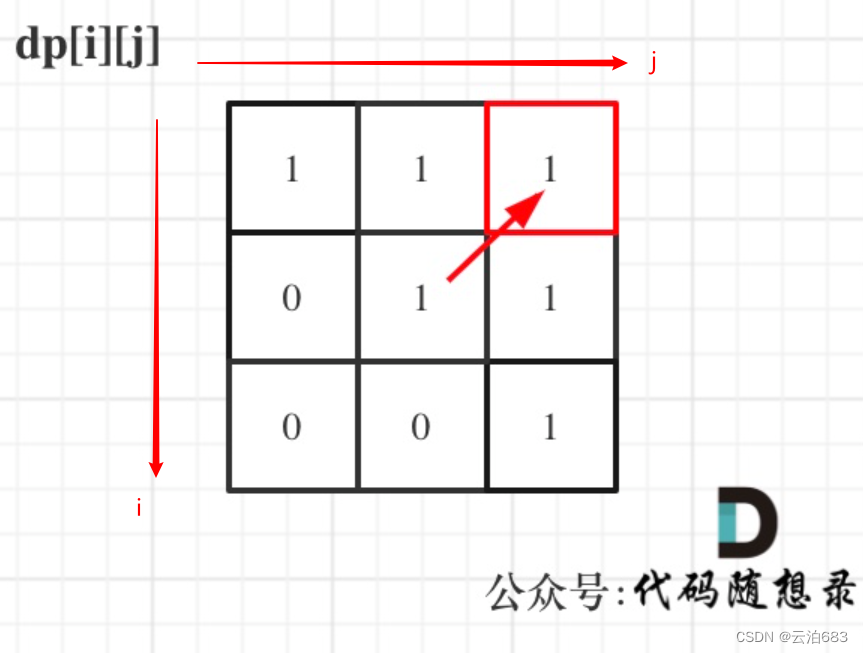
class Solution {
public:int countSubstrings(string s) {vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));int result = 0;for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序for (int j = i; j < s.size(); j++) {if (s[i] == s[j]) {if (j - i <= 1) { // 情况一 和 情况二result++;dp[i][j] = true;} else if (dp[i + 1][j - 1]) { // 情况三result++;dp[i][j] = true;}}}}return result;}
};可以观察到如果字符串匹配有两个判断链条,链条有result记录结果++,以及修改当前dp值为1,第一个遍历i的循环是从大到小遍历。
递推公式:
当s[i]与s[j]不相等,等于 不是回文串,默认false,不用操作
当s[i]与s[j]相等时,有如下三种情况
- 情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串(单个回文子串)
- 情况二:下标i 与 j相差为1,例如aa,也是回文子串(两个回文子串)
- 情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true,dp[i + 1][j - 1]的定义是表示区间范围[i,j]的子串是否是回文子串。(超过两个的回文子串)
if (s[i] == s[j]) {if (j - i <= 1) { // 情况一和情况二,i和j相等的时候0<1 相差1,1=1,所以两种情况包含在内result++;dp[i][j] = true;} else if (dp[i + 1][j - 1]) { // 情况三result++;dp[i][j] = true;}
}初始化都为false ,默认为ture就全是回文子串了
遍历顺序由于递推公式中,情况三是根据dp[i + 1][j - 1]是否为true,来对dp[i][j]进行赋值true
 这图可以看出dp[i][j]是由左下的dp[i + 1][j - 1]判断的,所以顺序需要
这图可以看出dp[i][j]是由左下的dp[i + 1][j - 1]判断的,所以顺序需要
从下到上,从左到右,来保证,递推公式可以推导。
总代码
在途中用result收集为子串的情况,末尾返回完成题目。
class Solution {
public:int countSubstrings(string s) {vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));int result = 0;for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序for (int j = i; j < s.size(); j++) {if (s[i] == s[j]) {if (j - i <= 1) { // 情况一 和 情况二result++;dp[i][j] = true;} else if (dp[i + 1][j - 1]) { // 情况三result++;dp[i][j] = true;}}}}return result;}
};516.最长回文子序列
题目:
给定一个字符串 s ,找到其中最长的回文子序列,并返回该序列的长度。
示例 1: 输入: "bbbab" 输出: 4 一个可能的最长回文子序列为 "bbbb"。
安装原始排序不变,不需要连续,凑成回文子序列。
dp数组含义:
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
递推公式:
s[i]与s[j]相同
dp[i][j] = dp[i + 1][j - 1] + 2;意为在原来是回文子序列的基础加上这两个相等的长度
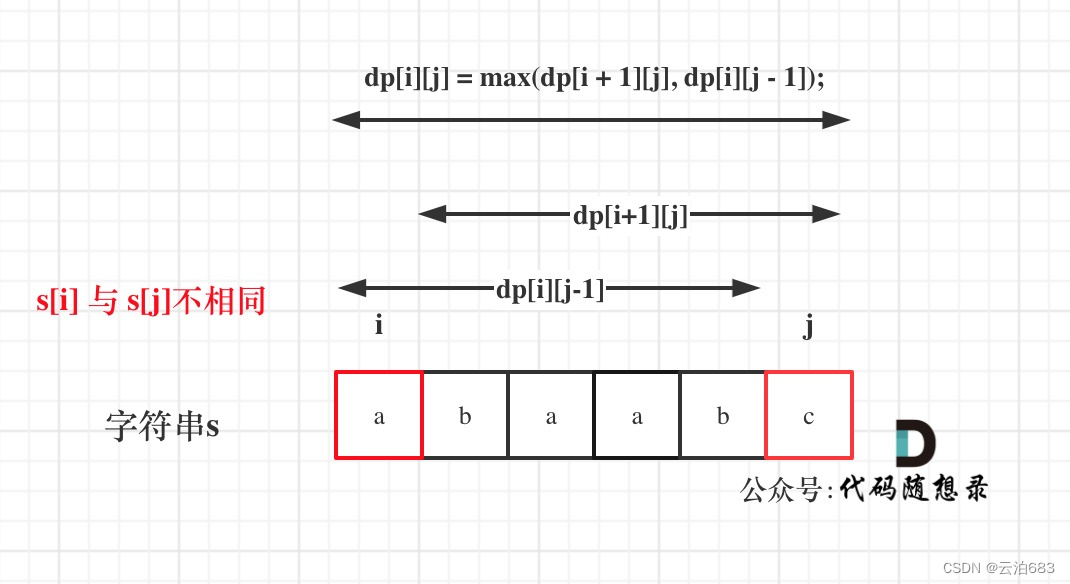
s[i]与s[j]不相同
说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]:dp[i + 1][j]。这个dp[i + 1][j]表示加了s[j]的最大回文子序长度,可以说加了s[j]的最大长度
加入s[i]:dp[i][j - 1]。这个dp[i][j - 1]表示加了s[i]的最大回文子序长度,可以说加了s[i]的最大长度
dp[i][j]取两者可能的最大长度,即dp[i][j]可以从加了那个字符推出最大长度,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
初始化:
首先要考虑当i 和j 相同的情况,从递推公式:dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出,i + 1 和 j - 1 一直往中间缩,给的字符集是奇数的话,会缩到一个字符上,这个时候dp[i][j]等于1,即:一个字符的回文子序列长度就是1。偶数个的话会彼此交过就是0?
vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
for (int i = 0; i < s.size(); i++) dp[i][i] = 1;遍历顺序:

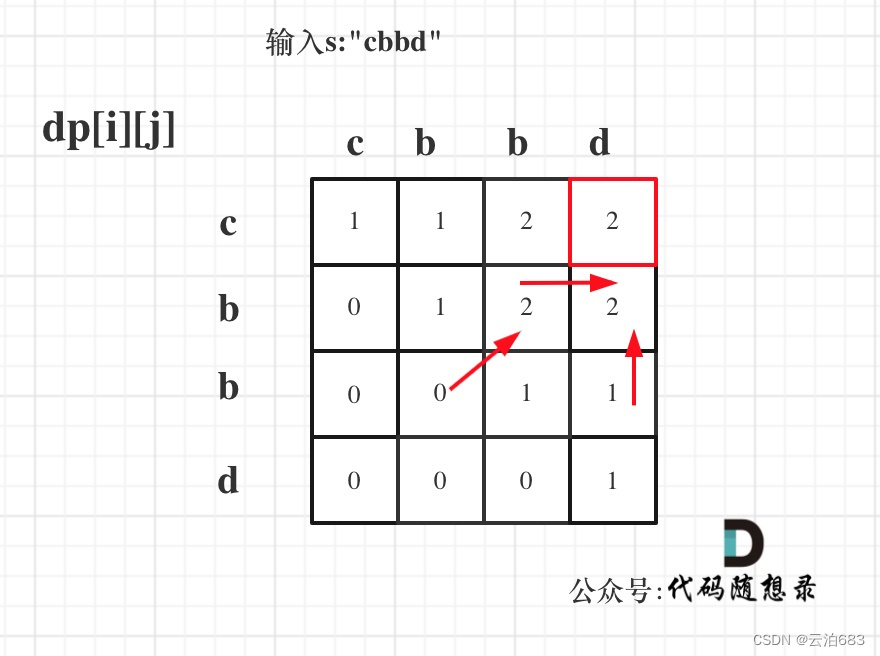
遍历i的时候一定要从下到上遍历,保证下一行的数据是经过计算的。
j的话,正常从左向右
总代码:
class Solution {
public:int longestPalindromeSubseq(string s) {vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));for (int i = 0; i < s.size(); i++) dp[i][i] = 1;for (int i = s.size() - 1; i >= 0; i--) {for (int j = i + 1; j < s.size(); j++) {if (s[i] == s[j]) {dp[i][j] = dp[i + 1][j - 1] + 2;} else {dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);}}}return dp[0][s.size() - 1];}
};相关文章:

647. 回文子串 516.最长回文子序列
647. 回文子串 题目: 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串,即使是由相…...

点云从入门到精通技术详解100篇-双传感器模式的非结构化环境检测与识别
目录 前言 国内外研究现状 可通行区域检测的研究 障碍物检测的研究...

Nginx-反向代理
反向代理 1 语法 server {listen 82; server_name www.liyong.f.com;location ~* .*(css|js|html|images). {proxy_pass http://11.22.19.81:8088; } 上面的示例的意思是: 当访问:http://www.liyong.f.com:82/static/css/OneMap.b728e2e4.css 转发到 …...
Java封装一个根据指定的字段来获取子集的工具类
工具类 ZhLambdaUtils SuppressWarnings("all") public class ZhLambdaUtils {/*** METHOD_NAME*/private static final String METHOD_NAME "writeReplace";/*** 获取到lambda参数的方法名称** param <T> parameter* param function functi…...

【HUST】网安纳米|2023年研究生纳米技术考试参考
目录 1 纳米材料是什么 2 纳米材料的结构特性 3 纳米结构的其他特性 4 纳米结构的检测技术 5 纳米材料的应用 打印建议:PPT彩印(这样重点比较突出),每面12张PPT,简单做一下关键词目录,亲测可以看清。如…...
【移远QuecPython】EC800M物联网开发板的MQTT协议腾讯云数据上报
【移远QuecPython】EC800M物联网开发板的MQTT协议腾讯云数据上报 文章目录 导入库初始化设置MQTT注册回调订阅发布功能开启服务发送消息函数打包调用测试效果附录:列表的赋值类型和py打包列表赋值BUG复现代码改进优化总结 py打包 导入库 from TenCentYun import TX…...
关灯游戏及扩展
7.8 图形界面应用案例——关灯游戏 题目: [案例]游戏初步——关灯游戏。 关灯游戏是很有意思的益智游戏,玩家通过单击关掉(或打开)一盏灯。如果关(掉(或打开)一个电灯,其周围(上下左右)的电灯也会触及开关,成…...
)
深度解析:用Python爬虫逆向破解dappradar的URL加密参数(最详细逆向实战教程,小白进阶高手之路)
特别声明:本篇文章仅供学习与研究使用,不得用做任何非法用途,请大家遵守相关法律法规 目录 一、逆向目标二、准备工作三、逆向分析 - 太详细了!3.1 逆向前的一些想法3.1.1 加密字符串属性猜测3.1.2 是否可以手动复制加密API?3.2 XHR断点调试3.3 加密前各参数属性的变化情况…...
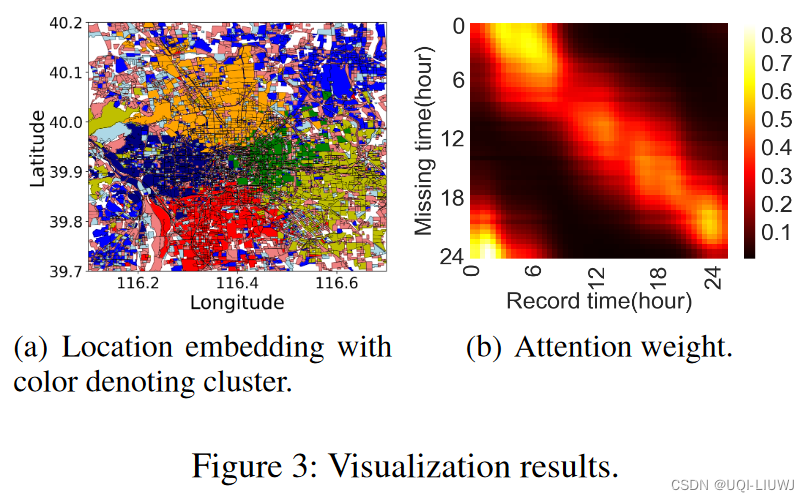
论文笔记:AttnMove: History Enhanced Trajectory Recovery via AttentionalNetwork
AAAI 2021 1 intro 1.1 背景 将用户稀疏的轨迹数据恢复至细粒度的轨迹数据是十分重要的恢复稀疏轨迹数据至细粒度轨迹数据是非常困难的 已观察到的用户位置数据十分稀疏,使得未观察到的用户位置存在较多的不确定性真实数据中存在大量噪声,如何有效的挖…...

Django之视图层
目录 一、三板斧的使用 二、JsonReponse序列化类的使用 三、 form表单上传文件 数据准备 数据处理 (1)post请求数据 (2)文件数据获取 四、 FBV与CBV 五、CBV的源码分析 as_view 方法 一、三板斧的使用 HttpResponse 返回字符串类型render 渲染html页面,并…...
DAY54 392.判断子序列 + 115.不同的子序列
392.判断子序列 题目要求:给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是…...
【Nginx】nginx | 微信小程序验证域名配置
【Nginx】nginx | 微信小程序验证域名配置 一、说明二、域名管理 一、说明 小程序需要添加头条的功能,内容涉及到富文本内容显示图片资源存储在minio中,域名访问。微信小程序需要验证才能显示。 二、域名管理 服务器是阿里云,用的宝塔管理…...

大数据Doris(二十二):数据查看导入
文章目录 数据查看导入 数据查看导入 Broker load 导入方式由于是异步的,所以用户必须将创建导入的 Label 记录,并且在查看导入命令中使用 Label 来查看导入结果。查看导入命令在所有导入方式中是通用的,具体语法可执行 HELP SHOW LOAD 查看。 show load order by create…...

STM32 I2C详解
STM32 I2C详解 I2C简介 I2C(Inter IC Bus)是由Philips公司开发的一种通用数据总线 两根通信线: SCL(Serial Clock)串行时钟线,使用同步的时序,降低对硬件的依赖,同时同步的时序稳定…...
)
软考 系统架构设计师系列知识点之云计算(1)
所属章节: 第11章. 未来信息综合技术 第6节. 云计算和大数据技术概述 大数据和云计算已成为IT领域的两种主流技术。“数据是重要资产”这一概念已成为大家的共识,众多公司争相分析、挖掘大数据背后的重要财富。同时学术界、产业界和政府都对云计算产生了…...
VS Code画流程图:draw.io插件
文章目录 简介快捷键 简介 Draw.io是著名的流程图绘制软件,开源免费,对标Visio,用过的都说好。而且除了提供常规的桌面软件之外,直接访问draw.io就可以在线使用,堪称百分之百跨平台,便捷性直接拉满。 那么…...
计算机 - - - 浏览器网页打开本地exe程序,网页打开微信,网页打开迅雷
效果 在电脑中安装了微信和迅雷,可以通过在地址栏中输入weixin:打开微信,输入magnet:打开迅雷。 同理:在网页中使用a标签,点击后跳转链接打开weixin:,也会同样打开微信。 运用同样的原理,在网页中点击超…...

C_6练习题
一、单项选择题(本大题共20小题,每小题2分,共40分。在每小题给出的四个备选项中,选出一个正确的答案,并将所选项前的字母填写在答题纸的相应位置上。) 下列叙述中正确的是()。 A.C语言程序将从源程序中第一个函数开始执行 B.可以在程序中由用户指定任意一个函数作为…...

XUbuntu22.04之安装pkg-config(一百九十二)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

【Proteus仿真】【51单片机】拔河游戏设计
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真51单片机控制器,使用按键、LED、动态数码管模块等。 主要功能: 系统运行后,指示灯处于中间位置,数码管显示得分0,当按下…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
