1334. 阈值距离内邻居最少的城市
分析题目两点“阈值距离”、“邻居最少”。
“阈值距离”相当于定了个上界,求节点之间的最短距离。
“邻居最少”相当于能连接的点的数量。
求节点之间的最短距离有以下几种方法:
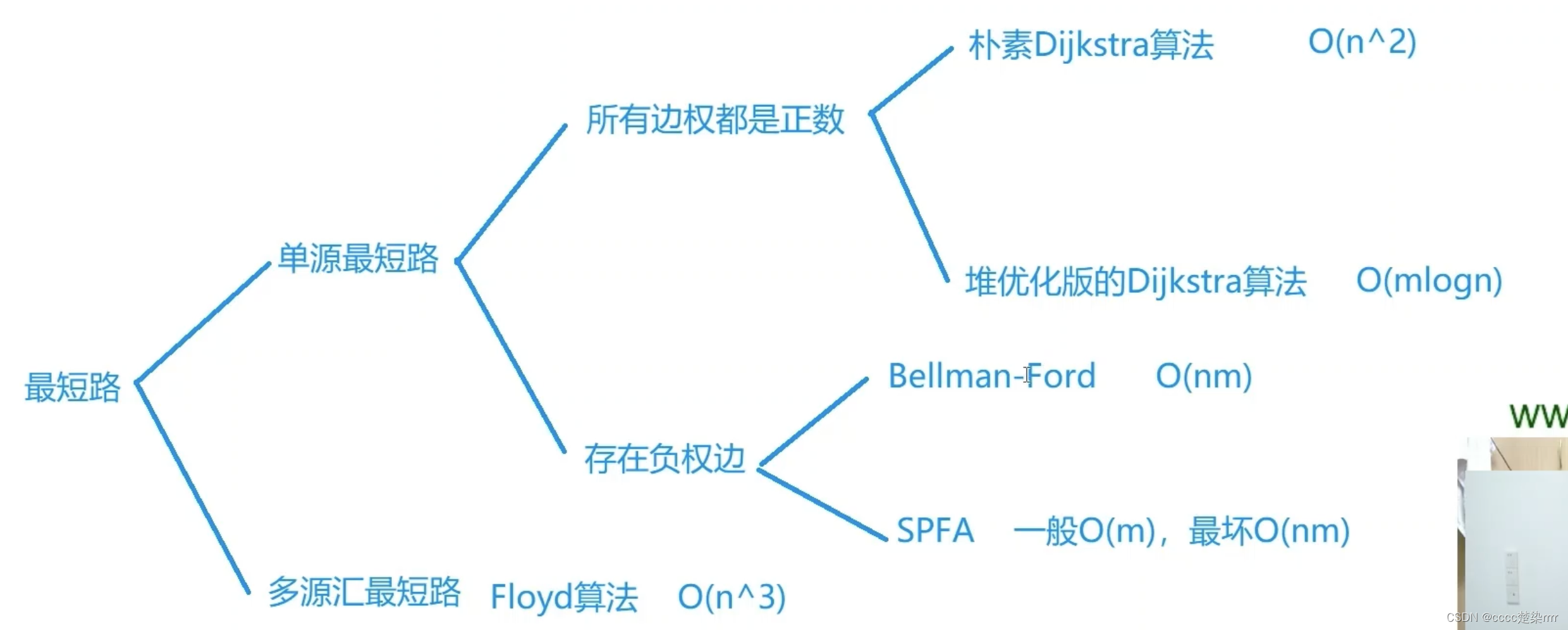
在这道题当中,n的范围是100以内,所以可以考虑O(n^3)的复杂度的算法
如果使用朴素Dijkstra算法,遍历所有点的算法复杂度为O(n*n^2)
如果使用堆优化版的Dijkstra算法,m=n^2,还不如朴素Dijkstra算法。
因此可以使用Floyd算法。
大致思路就是:先初始化一个最短距离矩阵d,然后每个节点一次遍历,对d值进行更新。
在这道题中,使用Floyd算法找到每个节点到其他节点的最短路径,然后遍历每个节点,找到在阈值距离内且可连接点数最少的节点。
class Solution {
public:int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {vector<vector<int>> d(n, vector<int>(n, 1e8)); // 这里的边值最大为1e4for (int i = 0; i < n; i++) d[i][i] = 0;for (auto v: edges) {int a = v[0], b = v[1], w = v[2];d[a][b] = d[b][a] = min(d[a][b], w); // 注意这里对边值的初始化要去最小值}for (int k = 0; k < n; k++) {for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {d[i][j] = min(d[i][j], d[i][k] + d[k][j]);}}}int res = -1, min_cnt = n + 1; // 初始下标和初始最小连接节点个数for (int i = 0; i < n; i++) {int cnt = 0;for (int j = 0; j < n; j++) {if (i != j && d[i][j] <= distanceThreshold) {cnt++;}}if (cnt <= min_cnt) {min_cnt = cnt;res = i;}}return res;}
};
相关文章:

1334. 阈值距离内邻居最少的城市
分析题目两点“阈值距离”、“邻居最少”。 “阈值距离”相当于定了个上界,求节点之间的最短距离。 “邻居最少”相当于能连接的点的数量。 求节点之间的最短距离有以下几种方法: 在这道题当中,n的范围是100以内,所以可以考虑O(n…...

Live800:客服行业的发展历程及未来前景
随着信息技术和互联网的高速发展,客服行业也在不断变革和发展。客服行业是一个服务型的行业,其发展历程也与人们对服务需求的变化密切相关。本文将介绍客服行业的发展历程和未来前景。 客服行业的发展历程 20世纪70年代,客服行业主要以电话服…...
exsi的安装和配置
直接虚拟真实机 vcent server 管理大量的exsi SXI原生架构模式的虚拟化技术,是不需要宿主操作系统的,它自己本身就是操作系统。因此,装ESXI的时候就等同于装操作系统,直接拿iso映像(光盘)装ESXI就可以了。 VMware vCente…...
基于springboot实现校园医疗保险管理系统【项目源码】
基于springboot实现校园医疗保险管理系统演示 系统开发平台 在线校园医疗保险系统中,Eclipse能给用户提供更多的方便,其特点一是方便学习,方便快捷;二是有非常大的信息储存量,主要功能是用在对数据库中查询和编程。其…...
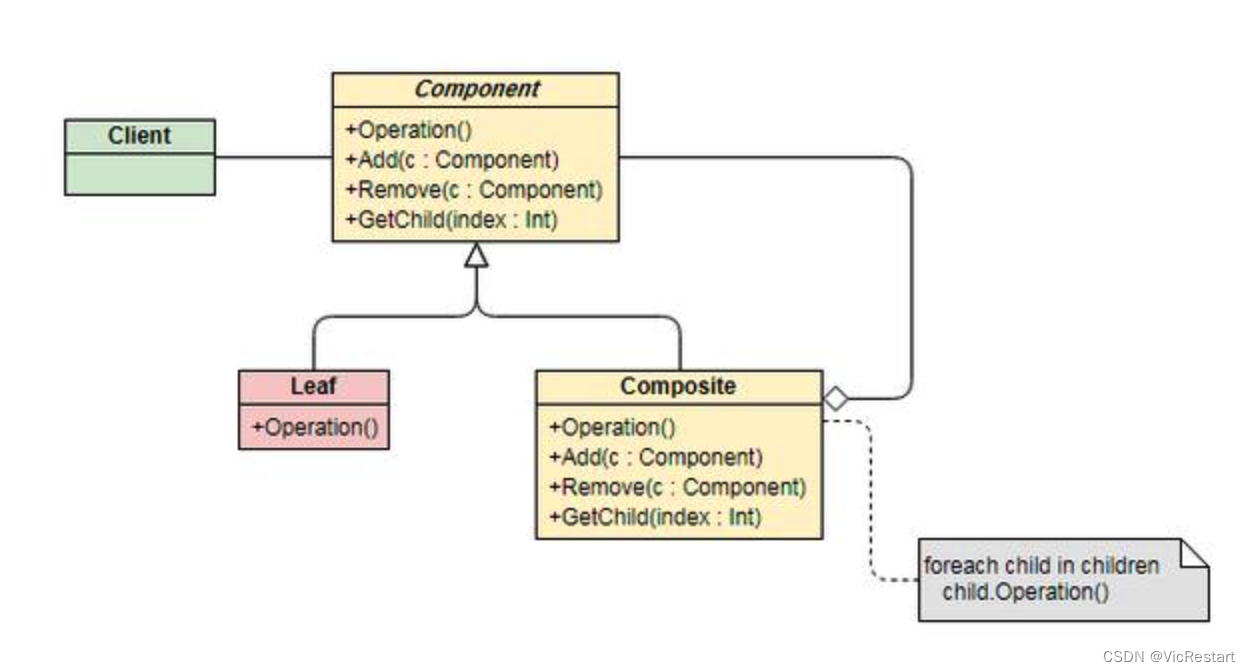
Python 如何实现组合(Composite)设计模式?什么是组合设计模式?
什么是组合(Composite)设计模式? 组合(Composite)设计模式是一种结构型设计模式,它允许客户端使用单一对象和组合对象(对象的组合形成树形结构)同样的方式处理。这样,客…...
编辑器vim和编译器gcc/g++
目录 一、编辑器vim 1、概念 2、基本操作 1、进入vim 2、模式切换 3、命令行模式 4、插入模式 5、底行模式 6、vim 的配置 二、编译器gcc/g 1、概念 2、背景知识 3、gcc/g中的编译链接 1、预处理 2、编译 3、汇编 4、链接 4、函数库 1、静态库 2、动态库 一…...
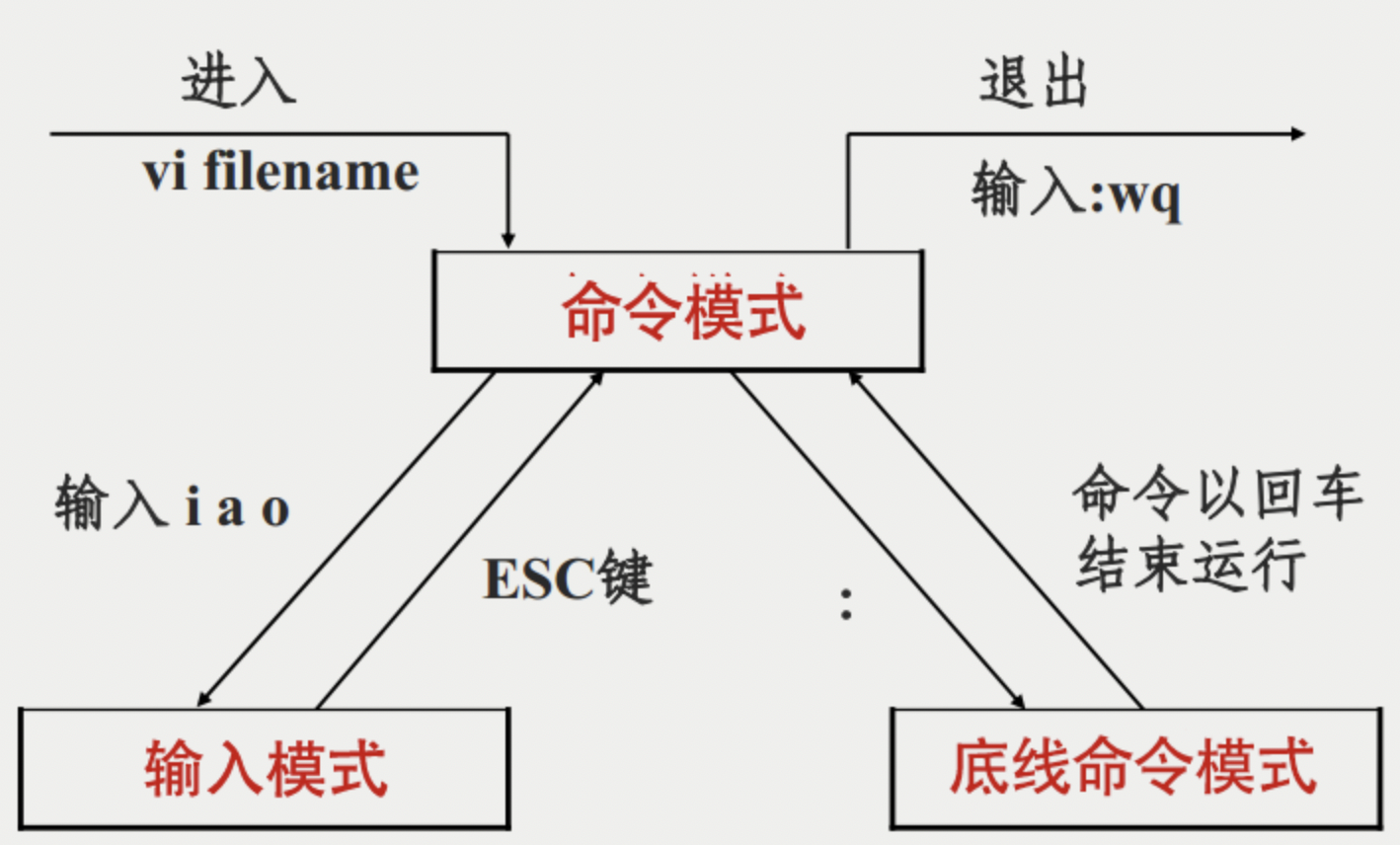
linux 系统下文本编辑常用的命令
一、是什么 Vim是从 vi 发展出来的一个文本编辑器,代码补全、编译及错误跳转等方便编程的功能特别丰富,在程序员中被广泛使用。 简单的来说, vi 是老式的字处理器,不过功能已经很齐全了,但是还是有可以进步的地方 而…...

3D Gaussian Splatting文件的压缩【3D高斯泼溅】
在上一篇文章中,我开始研究高斯泼溅(3DGS:3D Gaussian Splatting)。 它的问题之一是数据集并不小。 渲染图看起来不错。 但“自行车”、“卡车”、“花园”数据集分别是一个 1.42GB、0.59GB、1.35GB 的 PLY 文件。 它们几乎按原样…...
Spring Boot 整合xxl-job实现分布式定时任务
xxl-job介绍 XXL-JOB是一个分布式任务调度平台,其核心设计目标是开发迅速、学习简单、轻量级、易扩展。现已开放源代码并接入多家公司线上产品线,开箱即用。 xxl是xxl-job的开发者大众点评的许雪里名称的拼音开头。 设计思想 将调度行为抽象形成“调度…...

16.最接近的三数之和
题目来源: leetcode题目,网址:16. 最接近的三数之和 - 力扣(LeetCode) 解题思路: 对数组排序后,枚举第一个值,利用双指针在第一个值固定时的第二三个值。 解题代码:…...

php 插入排序算法实现
插入排序是一种简单直观的排序算法,它的基本思想是将一个数据序列分为有序区和无序区,每次从无序区选择一个元素插入到有序区的合适位置,直到整个序列有序为止 5, 3, 8, 2, 0, 1 HP中可以使用以下代码实现插入排序算法: functi…...

import gradio时出现SyntaxError: future feature annotations is not defined解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
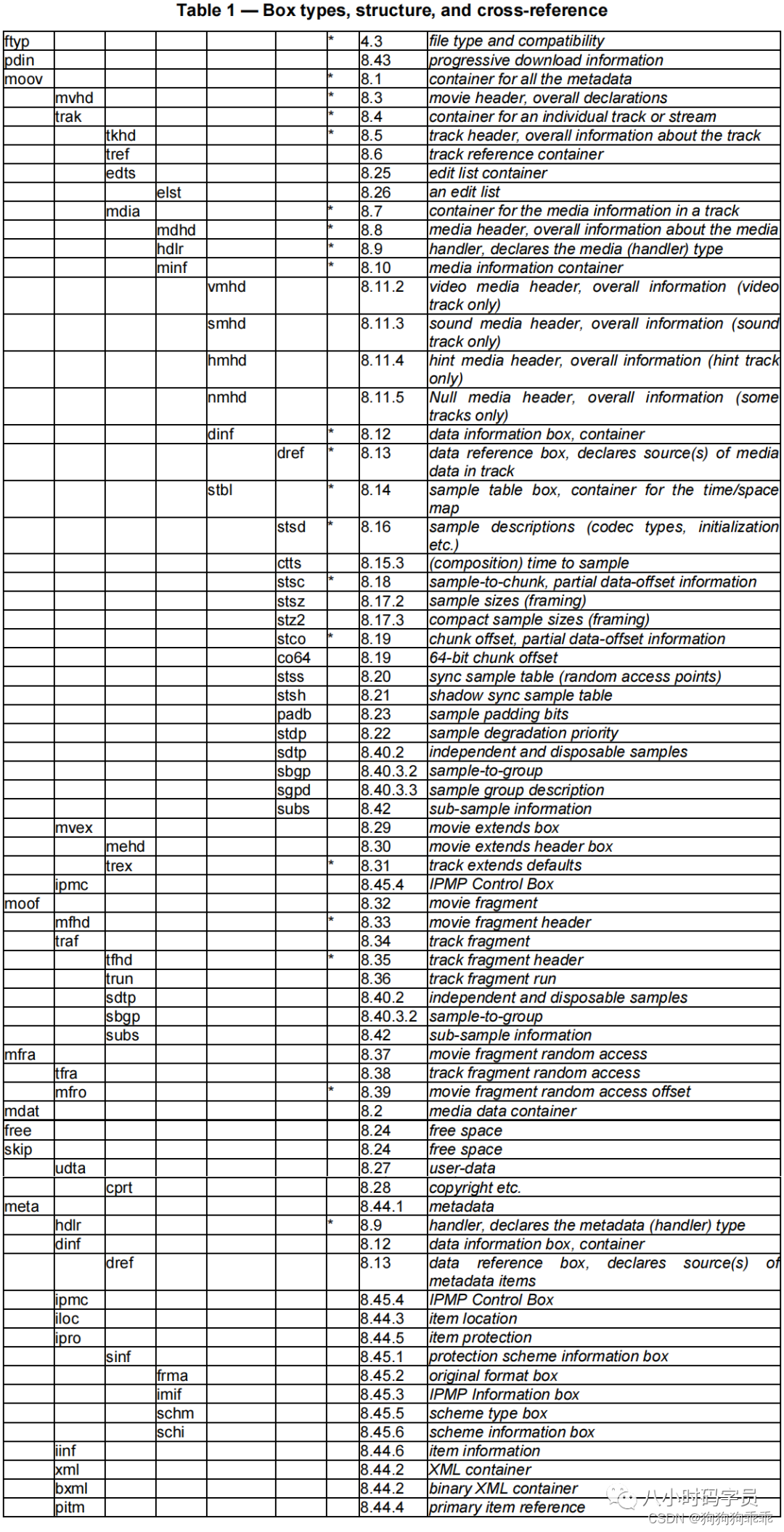
视频封装格式
FLV(Flash Video) FLV封装格式 Tag Data分为Audio,Video,Script三种 TS(Transport Stream)传输流 TS文件分为三层,(倒叙更好理解) TS层:在PES层基础上加入…...
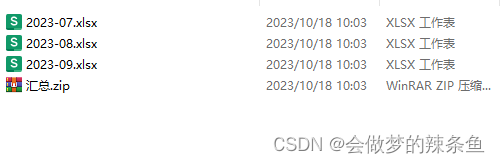
vue+iView实现下载zip文件导出多个excel表格
1,需求:在vue项目中,实现分月份导出多个Excel表格。 点击导出,下载zip文件,解压出多张表数据。 2,关键代码: <Button class"export button-style button-space" click"ex…...

Rust编程中的共享状态并发执行
1.共享状态并发 虽然消息传递是一个很好的处理并发的方式,但并不是唯一一个。另一种方式是让多个线程拥有相同的共享数据。在学习Go语言编程过程中大家应该听到过一句口号:"不要通过共享内存来通讯"。 在某种程度上,任何编程语言中的信道都类…...

python语法之数据类型
在python编程中,数据类型是一个重要的概念。 变量可以存储不同类型的数据,不同的类型可以做不同的事情。 Python在这些类别中默认内置了以下数据类型: 文本类型:str数值类型:int, float, complex序列类型:list, tup…...
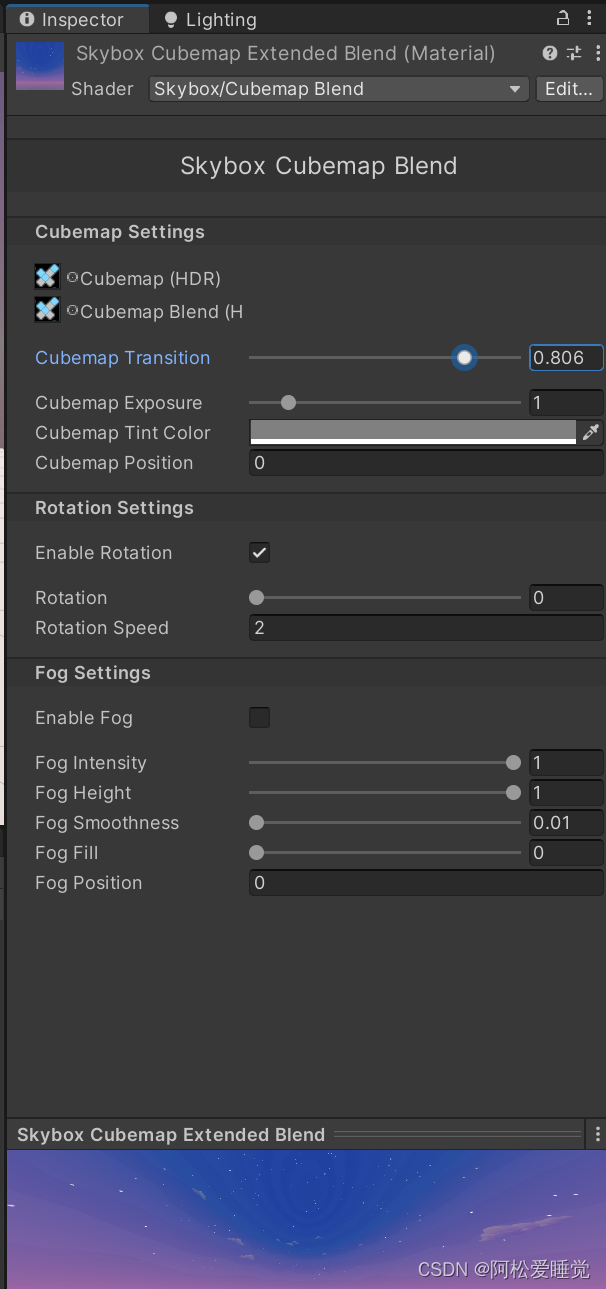
Skybox天空盒子的更换教程_unity基础开发教程
Skybox天空盒子的更换 Skybox的下载与导入更换SkyboxSkybox属性自定义 Skybox的下载与导入 打开资源商店 搜索FREE Skybox 这里是我使用的是这一款资源,点击添加至我的资源 打开包管理器Package Manager Packages选择My Assets 搜索Sky 选择刚刚添加的天空盒子 点…...
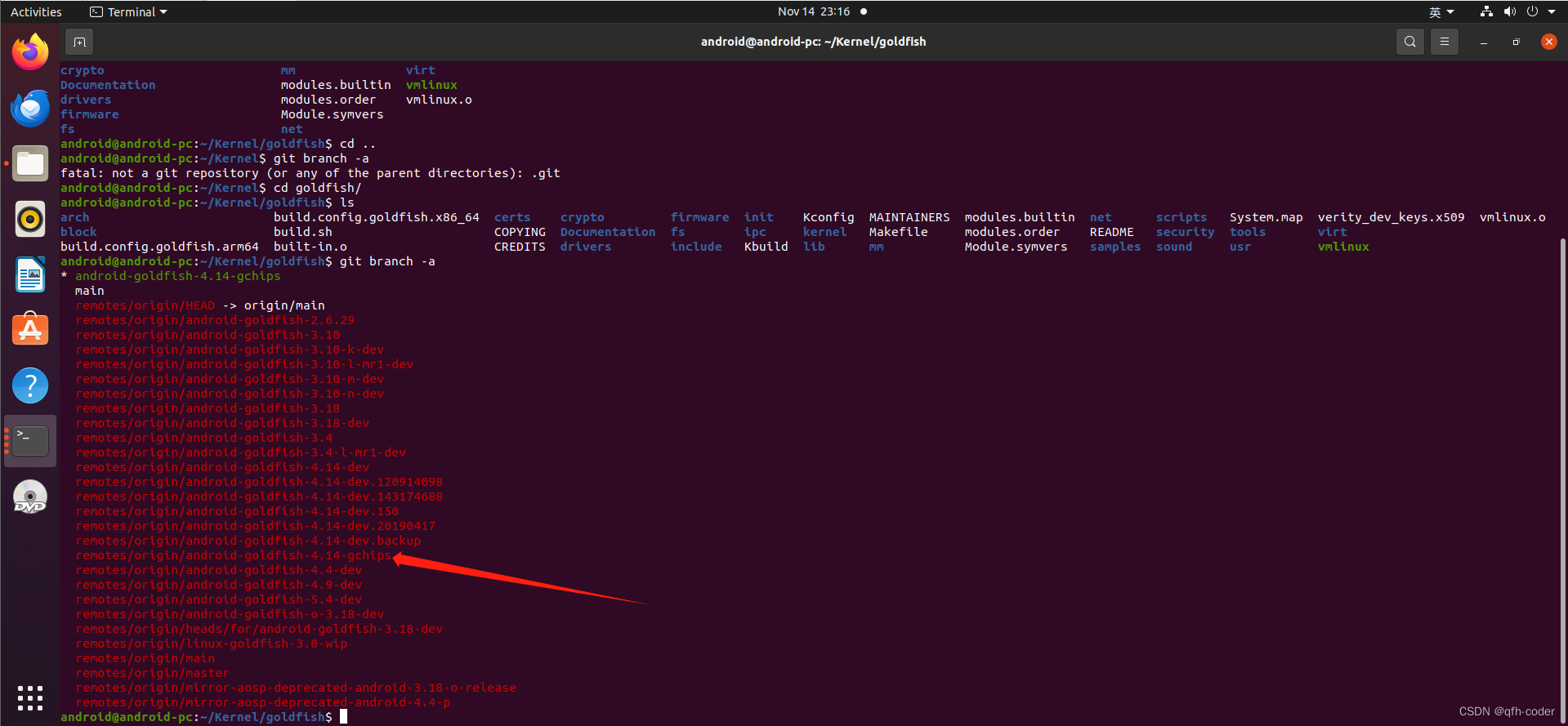
Android模拟器的linux内核源码的下载
文章目录 Android模拟器的linux内核源码的下载 Android模拟器的linux内核源码的下载 git clone https://aosp.tuna.tsinghua.edu.cn/android/kernel/goldfish.git自己新建一个文件夹存放内核代码,命名随意。 切换一下分支就有东西了 切换到下面这个分支...
Vue中methods实现原理
目录 前言 回调函数中的this指向问题 vue实例访问methods methods实现原理 前言 vue实例对象为什么可以访问methods中的函数方法?methods的实现原理是什么? 回调函数中的this指向问题 在解答前言中的问题前,需要了解一下回调函数中的th…...

维基百科是非营利性机构 词条内容具有中立性、准确性、可靠性
维基百科对一些企业很有神秘性,自行操作很多次也没有成功建立维基百科,这一定是没有按照维基百科的规则和流程去操作。小马识途营销顾问提醒企业,维基百科是一种基于协作的在线百科全书,由维基媒体基金会运营。维基百科的创建流程…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
