算法通关村——位运算之位移的妙用
位移的妙用
1、位1的个数
1.1、题目描述
LeetCode191. 编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位为 ‘1’ 的个数。
示例1:
输入:00000000000000000000000000001011
输出:3
示例2:
输入:00000000000000000100000000000000
输出:1
1.2、问题分析与解答
首先我们可以根据题目要求直接计算,题目给定的n是32位二进制表示下的一个整数,计算位1的个数的最简单的方法就是遍历n的二进制表示的每一位,判断每一位是否为1,同时进行计数。
那么怎么判断某一位是否为1呢?例如:00001001001000100001100010001001,首先我们注意要识别到最低位的1,可以这么做:
00001001001000100001100010001001& 00000000000000000000000000000001= 00000000000000000000000000000001
也就是说将原始数字和1进行与运算就能知道最低位是不是为1了,那其他位置该怎么算呢?
第一种思路是让原始数据不断右移或者是让1不断左移。例如将原始数据右移1位:
00000100100100010000110001000100& 00000000000000000000000000000001= 00000000000000000000000000000000
很显然此时可以判断出第二位是0,然后依次将原始数据右移就能判断出每个位置是否为1了。因此是不是1,计算一下(n >> i) & 1就可以了,代码如下:
public int hammingWeight(int n) {int count = 0;for (int i = 0; i < 32; i++) {count += (n >> i) & 1;}return count;
}
除了上述方法外,还有一种方法:
按位与运算有一个性质:对于整数n,计算n & (n - 1)的结果为将n的二进制表示的最后一个1变为0。
利用这条性质,令n = n & (n - 1),则n的二进制表示中的1的数量减少一个。重复该操作,知道n的二进制表示中的全部数位变为0,则操作次数即为n的位1的个数,还是看上面的例子:
n: 00000100100100010000110001000100
n-1: 00000100100100010000110001000011
n&(n-1): 00000100100100010000110001000000
可以看到此时n&(n-1)的结果比上一个n少了一个1,如果一直循环执行的话,到最后n等于0时退出循环,这时循环的次数就是原来n中1的个数,代码如下:
public int hammingWeight(int n) {int count = 0;while (n != 0) {n = n & (n - 1);count++;}return count;
}
2、比特位计数
2.1、问题描述
LeetCode338. 给你一个整数n,对于 0 <= i <= n 中的每一个i,计算其二进制表示中1的个数,返回一个长度为n + 1的数组ans作为答案。
示例:
输入:n=2
输出:[0, 1, 1]
解释:0到n有0,1,2三个数字,每个数字含有1的个数分别为0 1 1个,如下:
0 --> 0
1 --> 1
2 --> 10
2.2、问题分析与解答
本题是上题的扩展,可以直接遍历0到n的每个数,在遍历的过程中对每个数计算其位1的个数。
代码如下:
public int[] countBits(int n) {int[] bits = new int[n + 1];for (int i = 0; i <= n; i++) {bits[i] = countOnes(i);}return bits;
}public int countOnes(int x) {int ones = 0;while (x > 0) {x = x & (x - 1);ones++;}return ones;
}
相关文章:

算法通关村——位运算之位移的妙用
位移的妙用 1、位1的个数 1.1、题目描述 LeetCode191. 编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位为 ‘1’ 的个数。 示例1: 输入:00000000000000000000000000001011 输出࿱…...

【开题报告】基于uni-app的高校新生报道APP的设计与实现
1.选题背景和意义 随着高校规模的不断扩大和信息化技术的迅速发展,传统的高校新生报道方式已经无法满足日益增长的新生数量和信息处理的需求。传统的线下报道流程通常存在着信息收集效率低、报到流程繁琐等问题,给学生、教职工和管理人员带来了许多不便…...

Elasticsearch docker-compose 使用 Logstash 从 JSON 文件中预加载数据
在我们创建 Elasticsearch 进行开发时,最简单的办法就是在本地使用 docker-compose 来一键部署一个 Elasticsearch 集群。有时,特别是在准备测试环境时,开发人员希望从一开始就创建包含一些测试数据的数据库容器。我们可以使用 Logstash 来很…...

<文件操作及常用的API>
文章目录 专栏导读🚀简单认识一下文件🚀树形结构和目录🚀文件路径-相对路径、绝对路径🚀文件类型🚀Java中文件的操作🚀File 类的常用方法 专栏导读 🚀多线程章节 💐数据结构剖析 &am…...

深入探讨Linux中的文本文件查看命令
目录 前言1 cat命令2 less命令3 more命令4 head命令5 tail命令6 总结 前言 在Linux系统中,文本文件是日常工作中不可或缺的一部分,无论是配置文件、日志文件还是代码文件,都需要用到文本文件查看命令。在本文中,我们将深入研究一…...
asp.net企业员工档案信息管理系统VS开发sqlserver数据库web结构c#编程计算机网页源码项目
一、源码特点 asp.net企业员工档案信息管理系统 是一套完善的web设计管理系统,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。 asp.net企业员工档案信息管理系统 二、功能介绍 本系统使用Microsoft Visual Studio 2019为开发工具&…...

WPF中的xmlns 和xmlns:x有什么区别?
WPF (Windows Presentation Foundation) 中的 xmlns 和 xmlns:x 是XML命名空间的声明,它们在XAML(eXtensible Application Markup Language)中被广泛使用。XAML是WPF、Silverlight、Xamarin.Forms等技术中用于定义UI元素的标记语言。 xmlns: …...

为什么流量卡禁区多,而手机卡却可以用呢?
很多朋友比较关心流量卡禁区的问题,当我们申请流量卡时,运营商都会在套餐详情中标明具体的禁发地区,这个时候很多朋友都会有疑问了,为什么流量卡不能用的地区,可以申请到手机卡呢。 想要清楚这个问题࿰…...

Linux 桌面应用
Part I: Linux 系统概述 什么是 LinuxLinux 的历史和版本Linux 发行版介绍Linux 的优缺点 Part II: Linux 安装与配置 5. 硬件要求与准备工作 6. 安装 Linux 操作系统 7. Linux 系统初始化设置 8. Linux 系统更新与升级 9. Linux 基础配置 Part III: Linux 命令行 10. Linux…...

NLP领域的突破催生大模型范式的形成与发展
当前的大模型领域的发展,只是范式转变的开始,基础大模型才刚刚开始改变人工智能系统在世界上的构建和部署方式。 1、大模型范式 1.1 传统思路(2019年以前) NLP领域历来专注于为具有挑战性的语言任务定义和设计系统,…...
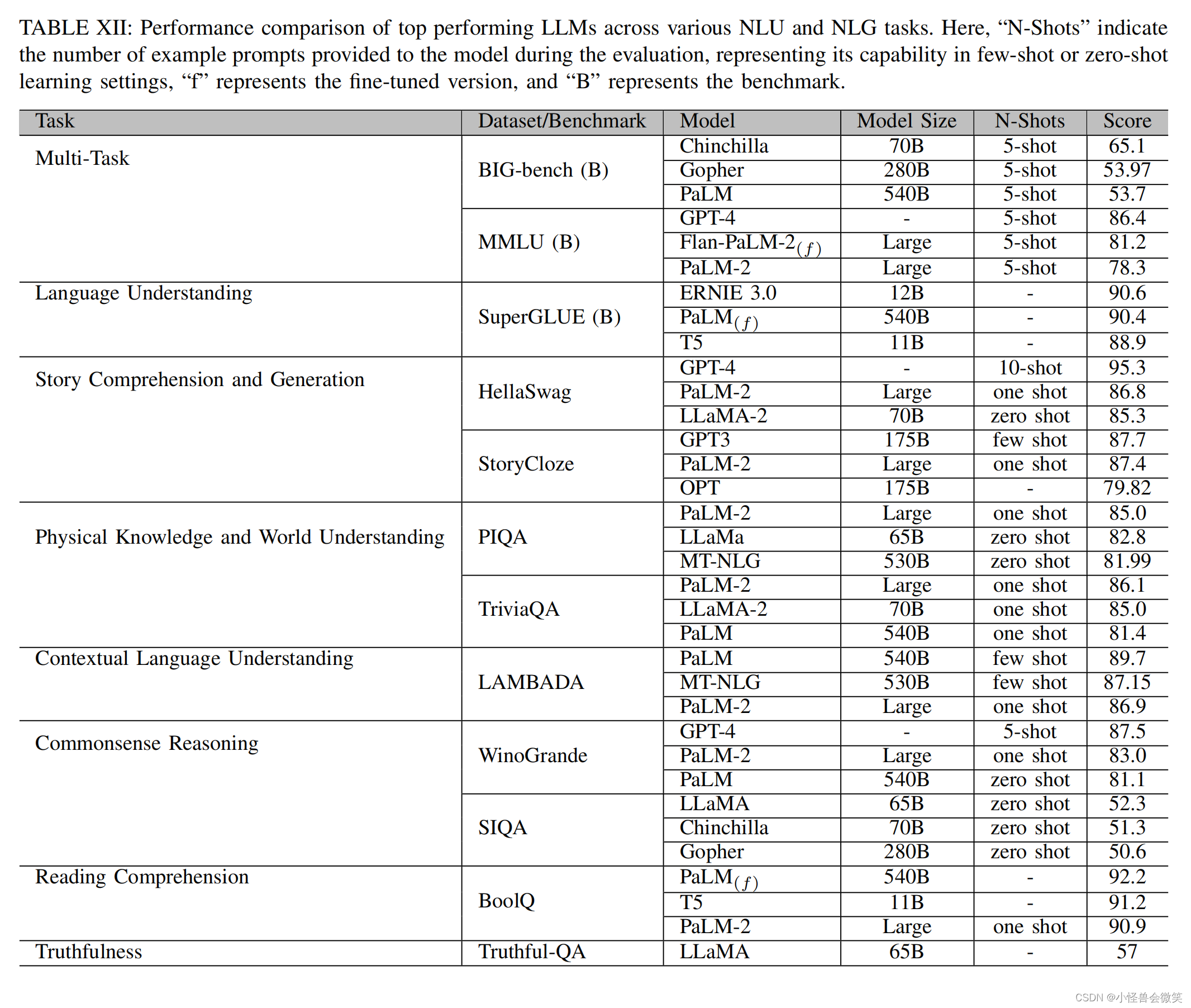
大模型的全面回顾,看透大模型 | A Comprehensive Overview of Large Language Models
大模型的全面回顾:A Comprehensive Overview of Large Language Models 返回论文和资料目录 论文地址 1.导读 相比今年4月的中国人民大学发表的大模型综述,这篇综述角度更侧重于大模型的实现,更加硬核,更适合深入了解大模型的一…...

【瑞禧分享】碳化硅纳米线 SiC纳米线 <100nm SiC晶须 SiC短纤维
碳化硅纳米线 规格或纯度:线/晶须含量:99% 供应商:西安瑞禧生物 英文名称:SiC Nanowire 别名:碳化硅纳米线,SiC晶须,SiC短纤维,SiC纳米线 英文别名:SiC Nanowire,SiC whiskers,SiC fiber 介绍&#x…...
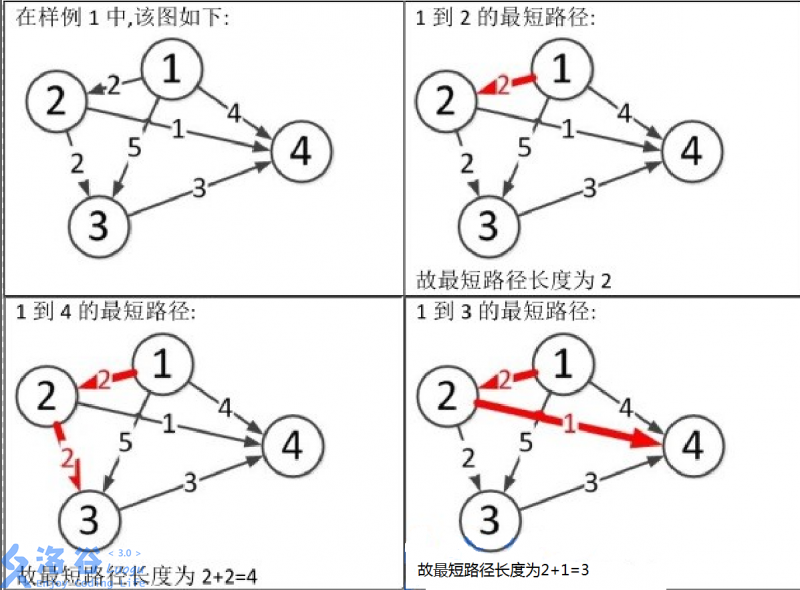
P3371 【模板】单源最短路径(弱化版)
【模板】单源最短路径(弱化版) 题目背景 本题测试数据为随机数据,在考试中可能会出现构造数据让SPFA不通过,如有需要请移步 P4779。 题目描述 如题,给出一个有向图,请输出从某一点出发到所有点的最短路…...
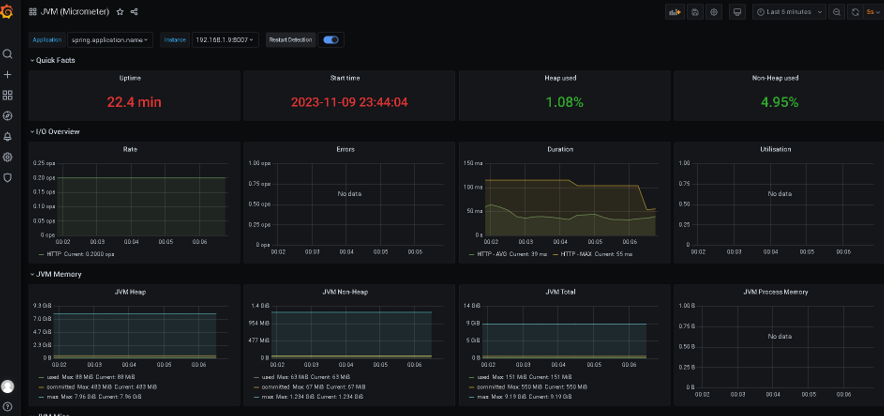
一文入门Springboot+actuator+Prometheus+Grafana
环境介绍 技术栈 springbootmybatis-plusmysqloracleactuatorPrometheusGrafana 软件 版本 mysql 8 IDEA IntelliJ IDEA 2022.2.1 JDK 1.8 Spring Boot 2.7.13 mybatis-plus 3.5.3.2 本地主机应用 192.168.1.9:8007 PrometheusGrafana安装在同一台主机 http://…...
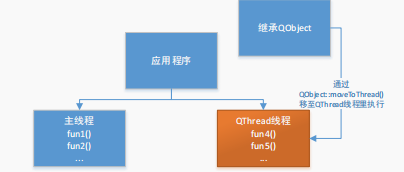
基于Qt 多线程(继承 QObject 的线程)
继承 QThread 类是创建线程的一种方法,另一种就是继承QObject 类。继承 QObject 类更加灵活。它通过 QObject::moveToThread()方法,将一个 QObeject的类转移到一个线程里执行。恩,不理解的话,我们下面也画个图捋一下。 通过上面的图不难理解,首先我们写一个类继承 QObj…...
图论11-欧拉回路与欧拉路径+Hierholzer算法实现
文章目录 1 欧拉回路的概念2 欧拉回路的算法实现3 Hierholzer算法详解4 Hierholzer算法实现4.1 修改Graph,增加API4.2 Graph.java4.3 联通分量类4.4 欧拉回路类 1 欧拉回路的概念 2 欧拉回路的算法实现 private boolean hasEulerLoop(){CC cc new CC(G);if(cc.cou…...
(一)什么是Vite——vite介绍与使用
什么是Vite Vite(法语意为 "快速的",发音 /vit/,发音同 "veet")是一种新型前端构建工具,能够显著提升前端开发体验。 它主要由两部分组成: 一个开发服务器,它基于 原生 …...

直流电动机四象限运行控制变流器设计
摘 要 节能和效率是工业经济发展的主题,电机在各行各业都是主要的动力来源, 直流电机以其控制简单,效率高,功率密度大等优势脱颖而出。基于直流电动机四象限运行控制变流器应用广泛,比如电子设备、电机控制、工业等行…...
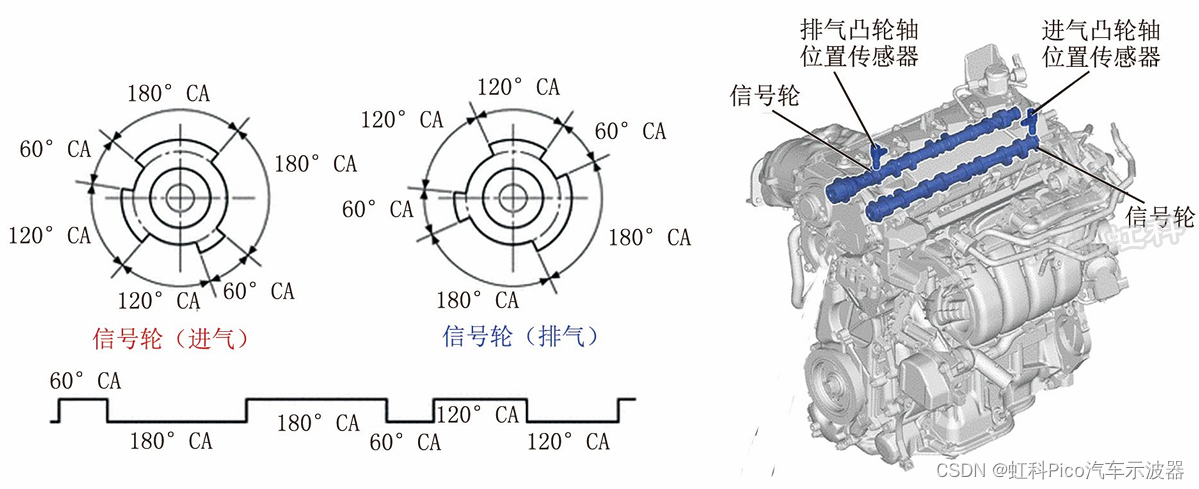
虹科示波器 | 汽车免拆检修 | 2021款广汽丰田威兰达PHEV车发动机故障灯异常点亮
一、故障现象 一辆2021款广汽丰田威兰达PHEV车,搭载A25D-FXS发动机和动力蓄电池系统(额定电压为355.2V,额定容量为45.0Ah),累计行驶里程约为1万km。车主反映,高速行驶时发动机突然抖动,且发动机…...

机器学习和深度学习领域的算法和模型
机器学习和深度学习领域有许多算法和模型,以下是一些常见的算法和模型: 线性回归(Linear Regression)逻辑回归(Logistic Regression)决策树(Decision Tree)随机森林(Ran…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
