2023NOIP A层联测32 sakuya
题目大意
有一棵有 n n n个节点的树,每条边有一个边权 w w w。有 m m m个特殊点,将这些点记为集合 A A A。
将 A A A中的元素随机打乱得到序列 a a a,求 ∑ i = 2 m d ( a i − 1 , a i ) \sum\limits_{i=2}^md(a_{i-1},a_i) i=2∑md(ai−1,ai)的期望值模 998244353 998244353 998244353后的值,其中 d ( x , y ) d(x,y) d(x,y)表示 x x x到 y y y的边权和。
有 q q q次修改,每次修改会将与 x x x相连的边的权值增加 k k k。求每次修改后上述式子的期望值。
1 ≤ n ≤ 5 × 1 0 5 , m ≤ n , 1 ≤ q ≤ 5 × 1 0 5 1\leq n\leq 5\times 10^5,m\leq n,1\leq q\leq 5\times 10^5 1≤n≤5×105,m≤n,1≤q≤5×105
1 ≤ w , k ≤ 1 0 9 1\leq w,k\leq 10^9 1≤w,k≤109
题解
对于每组特殊点 x , y x,y x,y,我们考虑有多少种方案会计算到 d ( x , y ) d(x,y) d(x,y)的贡献。在确定 x , y x,y x,y在 a a a中相邻之后,其他 m − 2 m-2 m−2个数有 ( m − 2 ) ! (m-2)! (m−2)!种放法, x , y x,y x,y中较前的数可以放在第一个到第 m − 1 m-1 m−1个位置上,确定了前一个数,则后一个数也确定了,而这两个数的顺序可以为 x , y x,y x,y或者 y , x y,x y,x,所以还要乘 2 2 2,也就是说有 2 ( m − 2 ) ! × ( m − 1 ) = 2 ( m − 1 ) ! 2(m-2)!\times (m-1)=2(m-1)! 2(m−2)!×(m−1)=2(m−1)!种方案会计算到 d ( x , y ) d(x,y) d(x,y)的贡献。而题目要求的是期望值,总共有 m ! m! m!种方案,那么 d ( x , y ) d(x,y) d(x,y)对答案的贡献为 2 ( m − 1 ) ! m ! × d ( x , y ) = 2 m × d ( x , y ) \dfrac{2(m-1)!}{m!}\times d(x,y)=\dfrac 2m\times d(x,y) m!2(m−1)!×d(x,y)=m2×d(x,y)。
下面,我们要求每条边被多少 d ( x , y ) d(x,y) d(x,y)计算过,这用一个 d f s dfs dfs即可算出,记这个值为 t d i td_i tdi。然后,求出所有边 i i i的 w i w_i wi与 t d i td_i tdi之积的和,也就是 ∑ i w i × t d i \sum\limits_iw_i\times td_i i∑wi×tdi, m 2 × ∑ i w i × t d i \dfrac m2\times \sum\limits_iw_i\times td_i 2m×i∑wi×tdi即为答案。
我们考虑每次修改对答案的贡献。设与 i i i相连的边的 t d td td值之和为 t w i tw_i twi,则每次修改会让 ∑ i w i × t d i \sum\limits_iw_i\times td_i i∑wi×tdi增加 k × t w i k\times tw_i k×twi。那么,我们可以 O ( 1 ) O(1) O(1)修改。因为题目只需要求答案,所以我们不需要真的去修改 w i w_i wi。
时间复杂度为 O ( n + q ) O(n+q) O(n+q)。
code
#include<bits/stdc++.h>
using namespace std;
const int N=500000;
const long long mod=998244353;
int n,m,q,z[N+5],siz[N+5];
long long ans,pt,w[N+5],td[N+5],tw[N+5];
vector<pair<int,int>>g[N+5];
long long mi(long long t,long long v){if(!v) return 1;long long re=mi(t,v/2);re=re*re%mod;if(v&1) re=re*t%mod;return re;
}
void dfs(int u,int fa){siz[u]=z[u];for(auto p:g[u]){int v=p.first,id=p.second;if(v==fa) continue;dfs(v,u);siz[u]+=siz[v];td[id]=1ll*(m-siz[v])*siz[v]%mod;}
}
int main()
{
// freopen("sakuya.in","r",stdin);
// freopen("sakuya.out","w",stdout);scanf("%d%d",&n,&m);for(int i=1,x,y;i<n;i++){scanf("%d%d%lld",&x,&y,&w[i]);g[x].push_back({y,i});g[y].push_back({x,i});}for(int i=1,x;i<=m;i++){scanf("%d",&x);z[x]=1;}dfs(1,0);for(int i=1;i<n;i++){ans=(ans+td[i]*w[i])%mod;}for(int i=1;i<=n;i++){for(auto p:g[i]){tw[i]=(tw[i]+td[p.second])%mod;}}scanf("%d",&q);long long tq=mi(m,mod-2)*2%mod;for(int o=1,x,k;o<=q;o++){scanf("%d%d",&x,&k);ans=(ans+tw[x]*k)%mod;pt=ans*tq%mod;printf("%lld\n",pt);}return 0;
}
相关文章:

2023NOIP A层联测32 sakuya
题目大意 有一棵有 n n n个节点的树,每条边有一个边权 w w w。有 m m m个特殊点,将这些点记为集合 A A A。 将 A A A中的元素随机打乱得到序列 a a a,求 ∑ i 2 m d ( a i − 1 , a i ) \sum\limits_{i2}^md(a_{i-1},a_i) i2∑md(ai−1…...
竞赛选题 深度学习的视频多目标跟踪实现
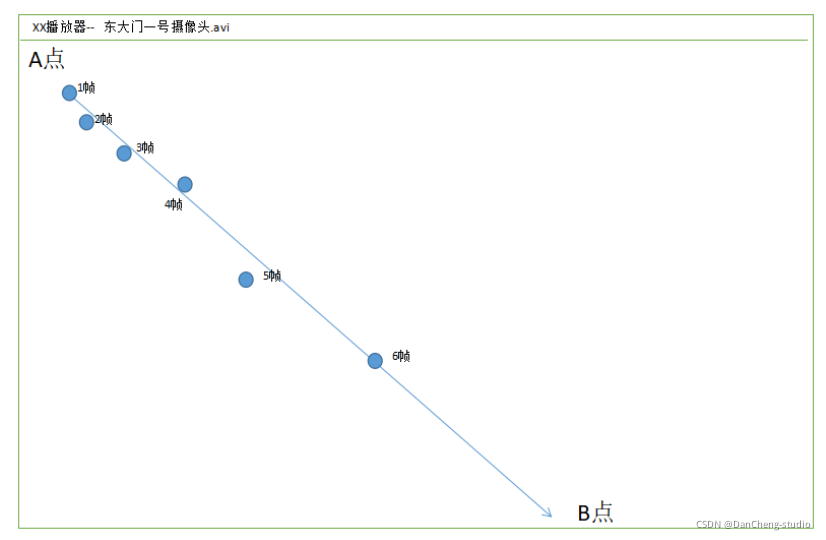
文章目录 1 前言2 先上成果3 多目标跟踪的两种方法3.1 方法13.2 方法2 4 Tracking By Detecting的跟踪过程4.1 存在的问题4.2 基于轨迹预测的跟踪方式 5 训练代码6 最后 1 前言 🔥 优质竞赛项目系列,今天要分享的是 基于深度学习的视频多目标跟踪实现 …...
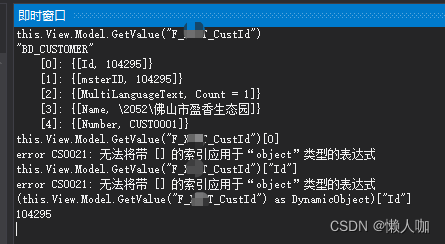
金蝶云星空表单插件获取控件值
文章目录 金蝶云星空表单插件获取控件值获取主键获取文本获取日期获取数值获取基础资料 金蝶云星空表单插件获取控件值 获取主键 正确: this.View.Model.GetPKValue();错误: 获取文本 this.View.Model.GetValue("FBILLNO")获取日期 thi…...

docker自启与容器自启
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...
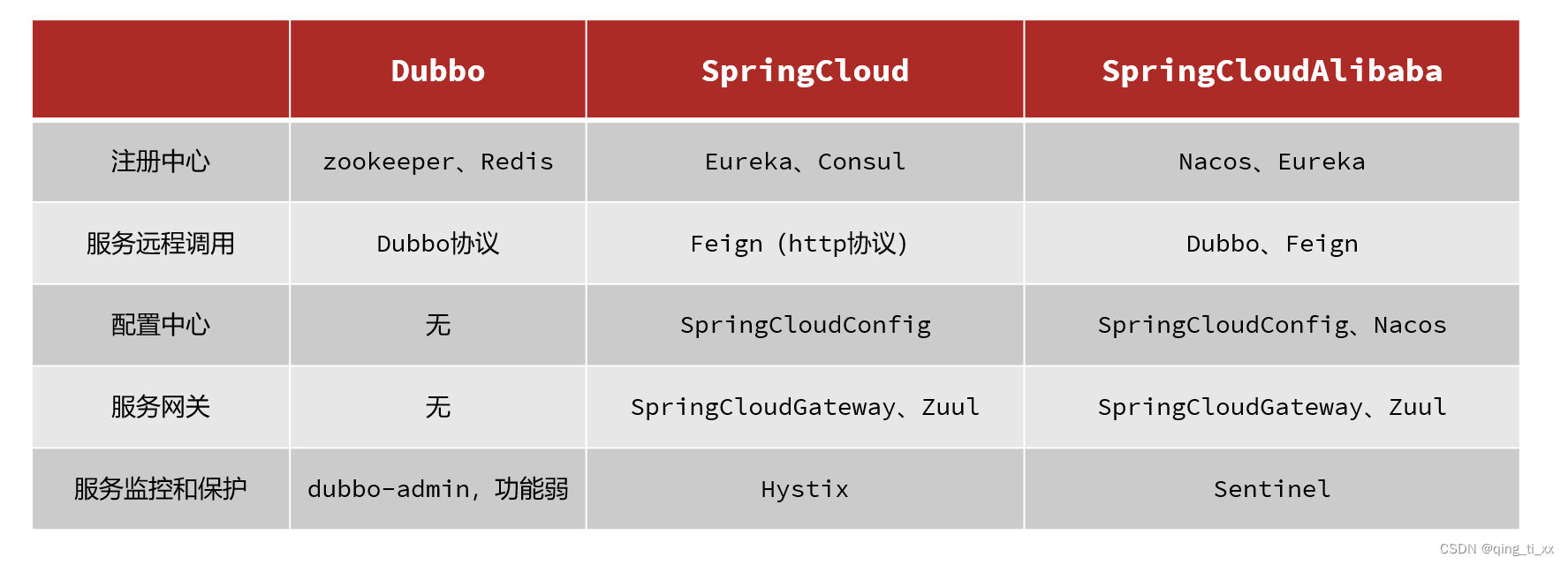
一、认识微服务
目录 一、单体架构 二、分布式架构 三、微服务 1、微服务架构特征: 1.单一职责: 2.面向服务: 3.自治: 4.隔离性强: 2、微服务结构: 3、微服务技术对比: 一、单体架构 二、分布式架构 三…...

Windows server 2012 R2系统服务器远程桌面服务激活服务器RD授权分享
Windows server 2012 R2系统服务器远程桌面服务激活服务器RD授权 二、激活服务器,获取许可证服务器ID和许可证密钥包ID三、激活终端服务器四、配置远程桌面会话主机授权服务器 上期我分享了Windows server 2012 R2系统服务器远程桌面服务的安装教程,若是…...

Vue的计算属性:让你的代码更简洁高效
Vue.js是一种流行的JavaScript框架,它提供了许多功能来帮助开发人员构建交互式Web应用程序。其中一个非常有用的功能是计算属性。在本文中,我们将讨论什么是Vue的计算属性以及如何使用它们来编写更简洁高效的代码。 什么是Vue的计算属性? Vu…...

mysql主从复制-使用心得
文章目录 前言环境配置主库从库 STATEMENTbinloggtidlog-errorDistSQL总结 前言 mysql 主从复制使用感受,遇到一些问题的整理,也总结了一些排查问题技巧。 环境 mysql5.7 配置 附:千万级数据快速插入配置可以参考:mysql千万数…...

今年副业比主业赚得多...
我是从20年开始接触副业的,主要是在程序员外包平台上接单。从一开始的月入0到几百,到现在每个月稳定有小一万的收入。这个月接了一个比较大的项目,结款之后发现今年的副业已经比主业赚得多了,简直美滋滋~ 今年主业收入8wÿ…...

debian12安装fail2ban
趁着阿里云活动,买了一台一年99的VPS,装了debian12 rootdebian:~# neofetch _,met$$$$$gg. …...
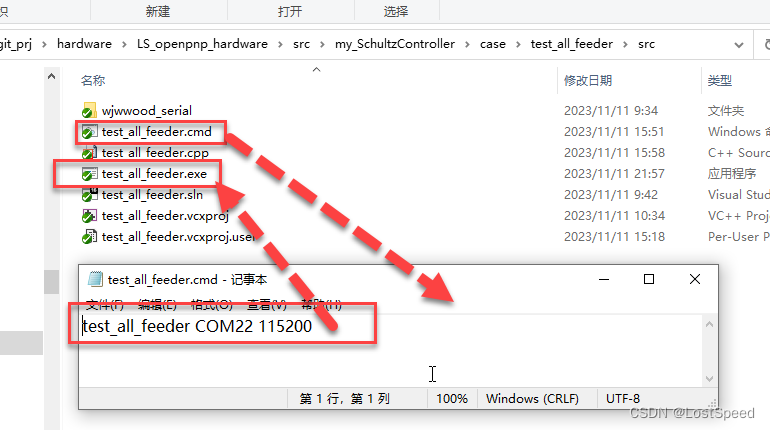
openpnp - 74路西门子飞达控制板(主控板STM32_NUCLEO-144) - 验证
文章目录 openpnp - 74路西门子飞达控制板(主控板STM32_NUCLEO-144) - 验证概述笔记重复数字IO的问题想法手工实现程序实现确定要摘掉的数字重合线自动化测试的问题测试程序的场景测试程序的运行效果测试程序实现备注END openpnp - 74路西门子飞达控制板(主控板STM32_NUCLEO-14…...

从房地产先后跨界通信、文旅演艺领域,万通发展未来路在何方?
近年来,房地产市场可谓负重前行,各大房企纷纷谋求新出路。 作为中国最早的房企之一,万通发展再次处在转型变革的十字路口。自去年以来,万通发展在转型升级之路上动作频频,可谓忙得不亦乐乎。 大幕落下之时,…...

LLM 中的参数单位
M (Mega) 相比于 Million: 1M (Mega) 在计算机科学中等于 ( 2^{20} )(即 1,048,576)字节。1 Million 等于 ( 10^6 )(即 1,000,000)。因此,1M (Mega) 在数字上略小于 1 Million。 G (Giga) 相比于 Billion&…...

【探索Linux】—— 强大的命令行工具 P.15(进程间通信 —— system V共享内存)
阅读导航 引言一、system V的概念二、共享内存(1) 概念(2) 共享内存示意图(3) 共享内存数据结构 三、共享内存的使用1. 共享内存的使用步骤(1)包含头文件(2)获取键值(ftok函数)(3)创…...
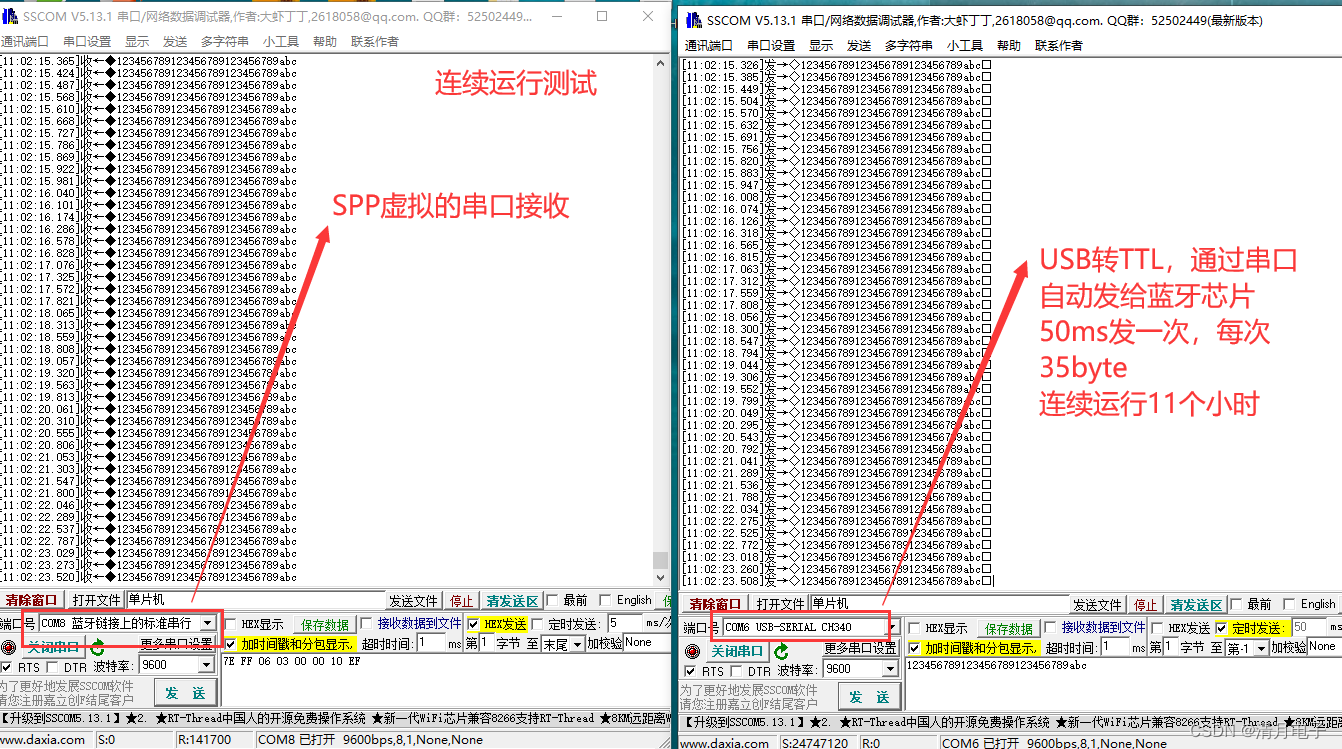
MCU通过KT6368A用SPP透传发送1K左右的数据,手机APP显示是3个包或者4个包,但是我看手册说最大一个包是512,理论应该是两个包吧,请问这正常吗?
一、问题简介 MCU通过KT6368A用SPP透传发送1K左右的数据,手机APP显示是3个包或者4个包,但是我看手册说最大一个包是512,理论应该是两个包吧,请问这正常吗? 详细说明 实际测试的截图如下:使用的是安卓app…...

童装CPC认证检测哪些内容?童装上架亚马逊美国站CPC认证办理
童装是指适合儿童穿着的服装。按年龄分,包括婴儿服装、儿童服装、童装、中年童装、大童服装。CPC认证即儿童产品证书(CPC),主要针对12岁以下的儿童,如玩具、摇篮、童装等。跨境卖家作为“进口商”,想要将中…...
2023鸿蒙预定未来,环境搭建学习
鸿蒙开发基础知识 鸿蒙的基本概念和特点 鸿蒙(HarmonyOS)是华为公司开发的一款全场景分布式操作系统。它的设计目标是为各种设备提供统一的、无缝的用户体验。鸿蒙的核心特点包括以下几个方面: 分布式架构:鸿蒙采用分布式架构&…...
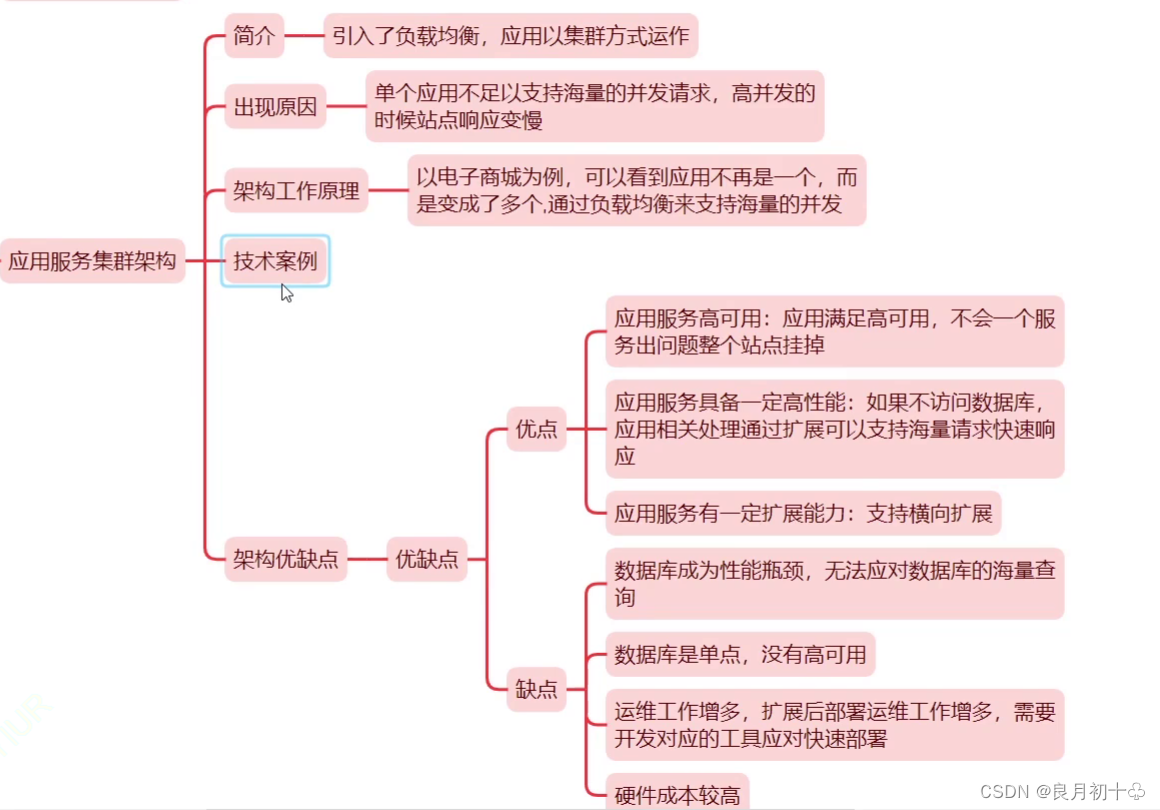
技术架构 - 应用数据分离,应用服务集群架构
前言 上一篇文章介绍了单机架构,由于性能瓶颈,满足不了高访问量,所以演化出了数据分离架构。 这种架构也很简单只是将应用服务和数据库服务分离开来,避免单一架构的资源争夺的情况。 一、 应用数据分离架构 1. 简介 应用服务和…...
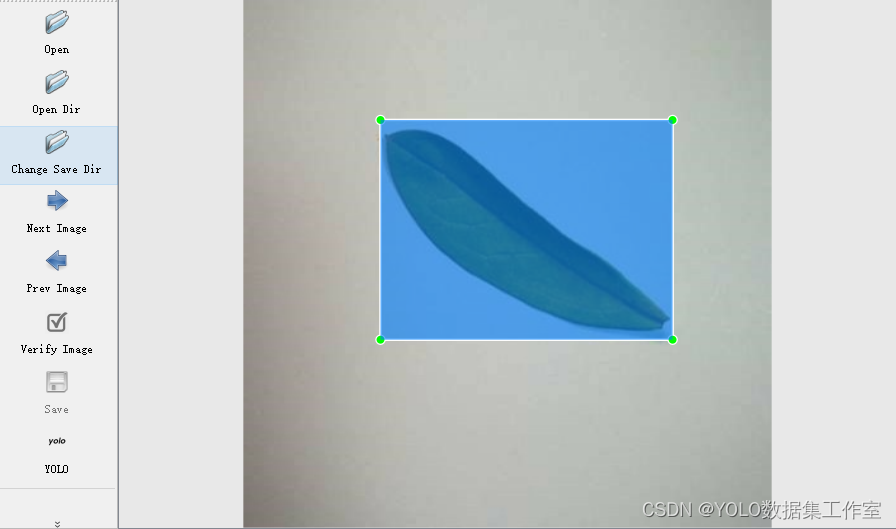
YOLO目标检测——树叶检测数据集下载分享【含对应voc、coco和yolo三种格式标签】
实际项目应用:生物多样性研究、林业管理、环境监测和教育科研等方面数据集说明:树叶分类检测数据,真实场景的高质量图片数据,数据场景丰富,总共十个类别。标签说明:使用lableimg标注软件标注,标…...
ubuntu 20通过docker安装onlyoffice,并配置https访问
目录 一、安装docker (一)更新包列表和安装依赖项 (二)添加Docker的官方GPG密钥 (三)添加Docker存储库 (四)安装Docker (五)启动Docker服务并设置它随系…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
