线性代数本质系列(二)矩阵乘法与复合线性变换,行列式,三维空间线性变换
本系列文章将从下面不同角度解析线性代数的本质,本文是本系列第二篇
向量究竟是什么?
向量的线性组合,基与线性相关
矩阵与线性相关
矩阵乘法与复合线性变换
三维空间中的线性变换
行列式
逆矩阵,列空间,秩与零空间
克莱姆法则
非方阵
点积与对偶性
叉积
以线性变换眼光看叉积
基变换
特征向量与特征值
抽象向量空间
快速计算二阶矩阵特征值
张量,协变与逆变和秩
文章目录
- 矩阵乘法与复合线性变换
- 三维空间中的线性变换
- 行列式
矩阵乘法与复合线性变换
我们已经知道矩阵是一种线性变换,现在对基向量连续施加两种线性变换,例如,先旋转,再剪切,其实,这在整体上可以看作是一种新的变换,这个新的变换被称为前两种独立变换的“复合变换”。
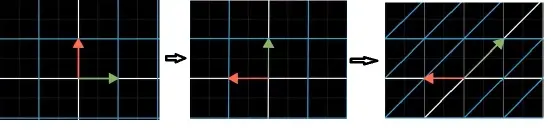
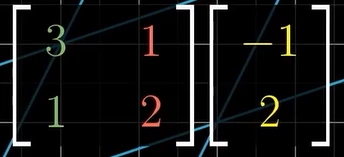
这个复合变换的矩阵可以通过追踪基向量的坐标得到,如上图所示,变换后的 i ⃗ \vec{i} i坐标 [ 1 1 ] \begin{bmatrix} 1\\ 1 \end{bmatrix} [11],变换后的 j ⃗ \vec{j} j坐标 [ − 1 0 ] \begin{bmatrix} -1\\ 0 \end{bmatrix} [−10],那么该复合变换矩阵就可以表示为: [ 1 − 1 1 0 ] \begin{bmatrix} 1 & -1\\ 1 & 0 \end{bmatrix} [11−10],当我们求一个向量经过复合变换后的坐标时,可以通过下图右边公式那样直接使用复合变换矩阵,而不需要像下图左边那样对向量连续施加两次单独的变换。

更一般地,对于矩阵乘法,我们就有了新的认识:他的几何意义是先施加一个变换,再施加另一个变换,施加顺序从右到左,顺序不同得到的结果也不同。

推广到更一般地数学含义: g ( f ( x ) ) g( f( x)) g(f(x))
根据前面章节学习到的知识,要想求线性变换对向量的作用,首先要得到变换后的基向量的坐标,让我们来看一个例子,假设连续施加两个线性变换 M 1 M_{1} M1和 M 2 M_{2} M2。
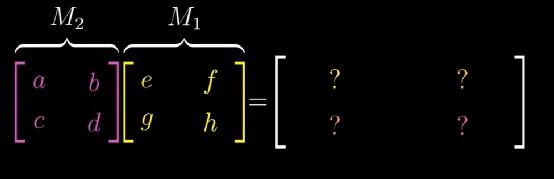
要想跟踪 i ⃗ \vec{i} i的去向,先看 M 1 M_{1} M1的第一列,这是经过 M 1 M_{1} M1变换后 i ⃗ \vec{i} i首先到达的地方: [ e g ] \begin{bmatrix} e\\ g \end{bmatrix} [eg],然后新的 i ⃗ \vec{i} i要经过 M 2 M_{2} M2的变换后到达最终目的地:
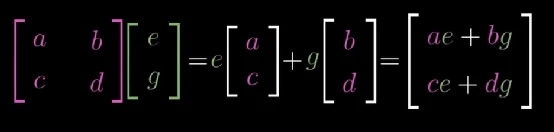
该结果作为复合矩阵的第一列, j ⃗ \vec{j} j经过同样的变换过程到达最终目的地,结果为复合变换矩阵第二列,复合变换的最终结果为:
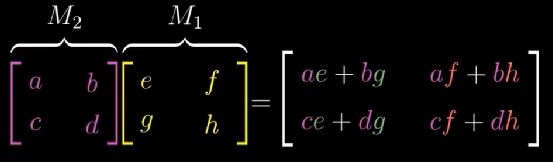
看,这不就是课堂上老师教的矩阵乘法计算规则嘛,只不过我们是从几何的角度推出来的。
大家可以从几何的角度来自行分析一下矩阵乘法的法则:
交换律: M 1 M 2 ≠ M 2 M 1 M_{1} M_{2} \neq M_{2} M_{1} M1M2=M2M1
结合率:(AB)C=A(BC)
三维空间中的线性变换
前面一直在讨论二维情况,也就是将二维向量映射成二维向量,其实,只要掌握了二维线性变换的核心本质,就能轻松的扩展到更高维的空间中。
三维空间变换以三维向量为输入,以三维向量为输出,和二维向量一样,一个线性变换是在操纵三维空间中所有的点,变换后保持空间中网格线等距且原点不变。

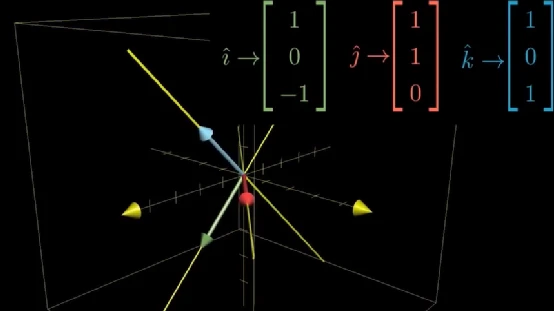
与二维一样,三维线性变换也是由基向量的去向完全决定,只不过基向量由 i ⃗ \vec{i} i, j ⃗ \vec{j} j变成了 i ⃗ \vec{i} i, j ⃗ \vec{j} j, k ⃗ \vec{k} k,例如,我们得到变换后三个基向量的坐标,那么由三个新的基向量组成矩阵就是三维线性变换矩阵 [ 1 1 1 0 1 0 − 1 0 1 ] \begin{bmatrix} 1 & 1 & 1\\ 0 & 1 & 0\\ -1 & 0 & 1 \end{bmatrix} 10−1110101 。
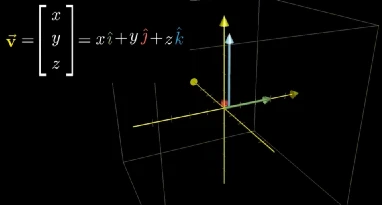
要想计算一个向量经过上面的三维变换后的新坐标,同样可以参照二维空间的计算方式,结果向量是基向量的线性组合。
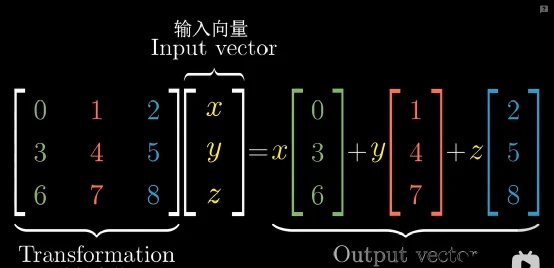
同理两个三维矩阵的相乘也可以合并成一个复合变换矩阵,三维变换在计算机图形学中有着广泛的应用。
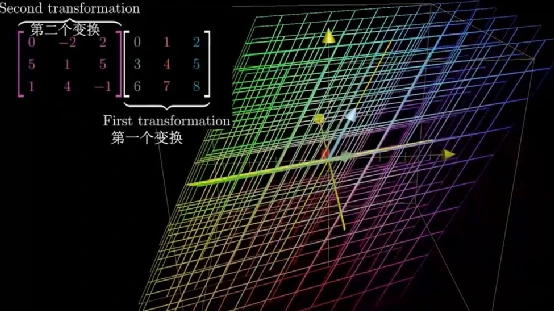
三维矩阵的乘法同样遵循二维矩阵乘法的思路。
行列式
前面我们从几何的角度对线性变换有了很直观的认识,其中有的线性变换对空间向外拉伸,有的则是将空间向内挤压。
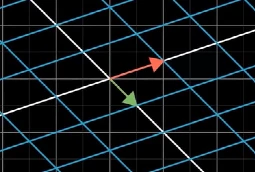
向内挤压
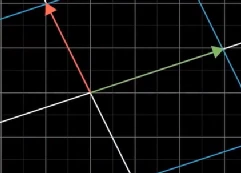
向外拉伸
有一种方法对于理解这些线性变换很有用,那就是准确测量向内挤压了多少,向外拉伸了多少,更具体地讲就是计算出一个区域增大或减少的比例。
让我们来看一个例子,假设一个线性变换矩阵 [ 3 0 0 2 ] \begin{bmatrix} 3 & 0\\ 0 & 2 \end{bmatrix} [3002],变换前基向量形成的四边形面积为1。
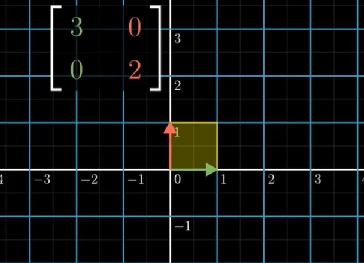
变换后,如下图,基向量形成一个2*3的矩形,面积为6
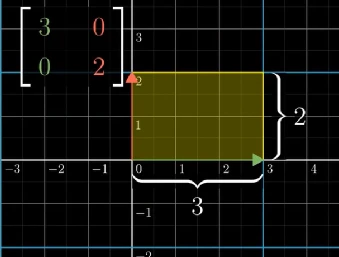
所以我们说这个变换将基向量形成的方格拉伸了6倍,根据线性变换的性质,如下图,所有可形成的区域都被拉伸了同样的大小。
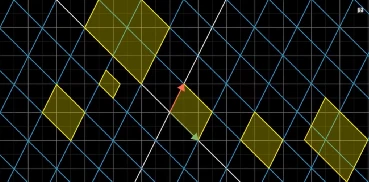
现在,我们要抛出一个重磅信息:这个面积的变化的比例值就是该线性变换矩阵的行列式,这就是行列式的几何意义。

如果行列式值大于1,则代表该线性变换矩阵将一个区域进行拉伸,大于0且小于1的数代表缩小,负数代表反方向缩放。
注意,如果一个线性变换矩阵的行列式为0,则代表该变换将一个区域压缩成了一条线或者是一个点,从几何意义上讲,也就是说该变换将空间压缩到了更小的维度上,这在我们后面判断线性方程组是否有解提供了重要依据。

同理,三维线性变换的行列式代表的则是体积的变换比例,如下图,一个以初始基向量形成的111的立方体经过线性变换后该体积变成了如下图的大小。
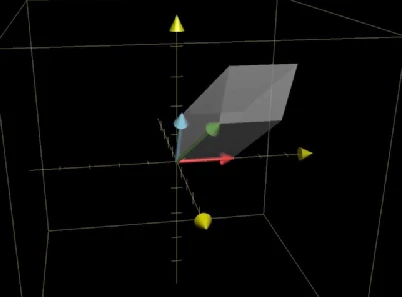
三维变换矩阵的行列式为0,代表空间被压缩成了一个面,或者一个点,如果行列式是负数,说明空间定向已经发生改变,不能用右手定则描述基向量之间的关系。
前面说了行列式的几何意义,那如何求一个矩阵的行列式呢?
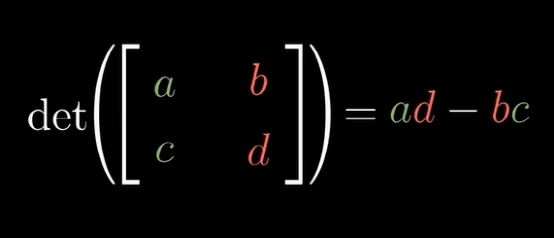
上图是一个行列式的计算公式,那它的几何意义是什么呢?如下图,假设给定一个特殊矩阵 [ a 0 0 d ] \begin{bmatrix} a & 0\\ 0 & d \end{bmatrix} [a00d], i ⃗ \vec{i} i被缩放了a倍, j ⃗ \vec{j} j被缩放了d倍,变换前后面积缩放了ad倍,这正符合行列式计算公式的结果。
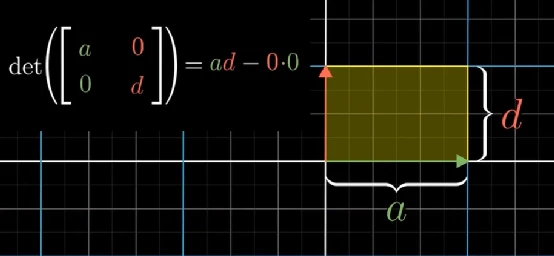
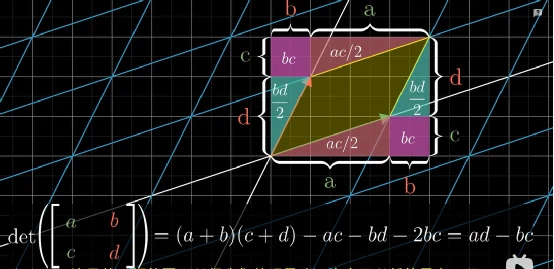
前面我们给出了一个特殊的例子,但推广到更一般的矩阵,也是满足上面公式的。
相关文章:

线性代数本质系列(二)矩阵乘法与复合线性变换,行列式,三维空间线性变换
本系列文章将从下面不同角度解析线性代数的本质,本文是本系列第二篇 向量究竟是什么? 向量的线性组合,基与线性相关 矩阵与线性相关 矩阵乘法与复合线性变换 三维空间中的线性变换 行列式 逆矩阵,列空间,秩与零空间 克…...

Linux-CentOS重要模块
软件包管理器:CentOS使用Yum(Yellowdog Updater, Modified)作为其包管理器。Yum提供了一种方便的方式来安装、更新和删除软件包,并自动解决依赖关系。 RPM:RPM(RPM Package Manager)是CentOS中…...
posix定时器的使用
POSIX定时器是基于POSIX标准定义的一组函数,用于实现在Linux系统中创建和管理定时器。POSIX定时器提供了一种相对较高的精度,可用于实现毫秒级别的定时功能。 POSIX定时器的主要函数包括: timer_create():用于创建一个定时器对象…...

安科瑞煤矿电力监控系统的研究与应用
摘要:作为一个巨大的能源消耗国家,我国每年对煤炭的市场需求巨大。煤炭作为我国点力气和供暖企业的重要原材料,煤矿的开采过程存在着难以消除的风险,我国的煤炭安全问题长期困扰着相关企业和监督部门,也受到社会的广泛…...
)
高教社杯数模竞赛特辑论文篇-2023年A题:基于机理分析法的定日镜场优化设计模型(附获奖论文及MATLAB代码实现)
目录 摘要 一、 问题重述 1 . 1 问题背景 1 . 2 问题要求 二、 问题分析...
缩点+图论路径网络流:1114T4
http://cplusoj.com/d/senior/p/SS231114D 重新梳理一下题目 我们先建图 x → y x\to y x→y,然后对点分类:原串出现点,原串未出现点。 假如我们对一个原串出现点进行了操作,那么它剩余所有出边我们立刻去操作必然没有影响。所…...
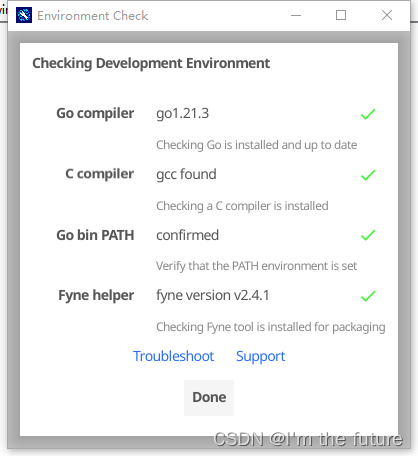
Go语言fyne开发桌面应用程序-环境安装
环境安装 参考https://developer.fyne.io/started/#prerequisites网站 之前的文章介绍了如何安装GO语言这里不在叙述 msys2 首先安装msys2,https://www.msys2.org/ 开始菜单打开MSYS2 执行 $ pacman -Syu$ pacman -S git mingw-w64-x86_64-toolchain注意&#…...
JavaWeb——CSS3的使用
目录 1. CSS概述 2. CSS引入方式 3. CSS颜色显示 4. CSS选择器 4.1. 元素(标签)选择器 4.2. id选择器 4.3. 类选择器 4.4. 三者优先级 5. 盒子模型 1. CSS概述 CSS,全称为“Cascading Style Sheets”,中文译为“层叠样式…...

AR导览小程序开发方案
一、背景介绍 随着科技的不断发展,虚拟现实(VR)和增强现实(AR)技术逐渐被应用于各个领域。其中,AR导览小程序作为一种新兴的导览方式,以其独特的视觉体验和互动性受到了广泛的关注。AR导览小程…...
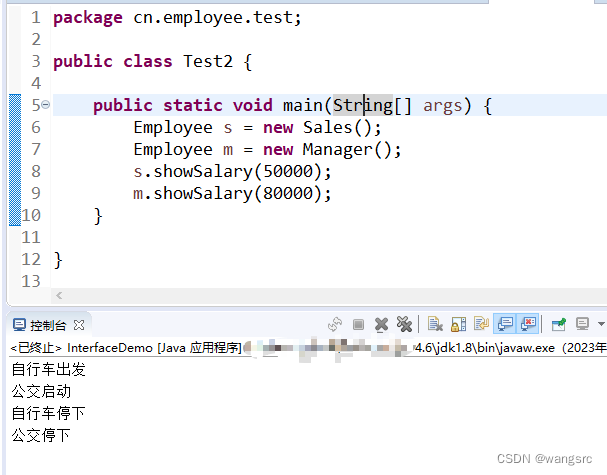
继承、多态
复习 需求: 编写一个抽象类:职员Employee,其中定义showSalary(int s)抽象方法;编写Employee的子类,分别是销售员Sales和经理Manager,分别在子类中实现对父类抽象方法的重写,并编写测试类Test查看输出结果 package cn.…...
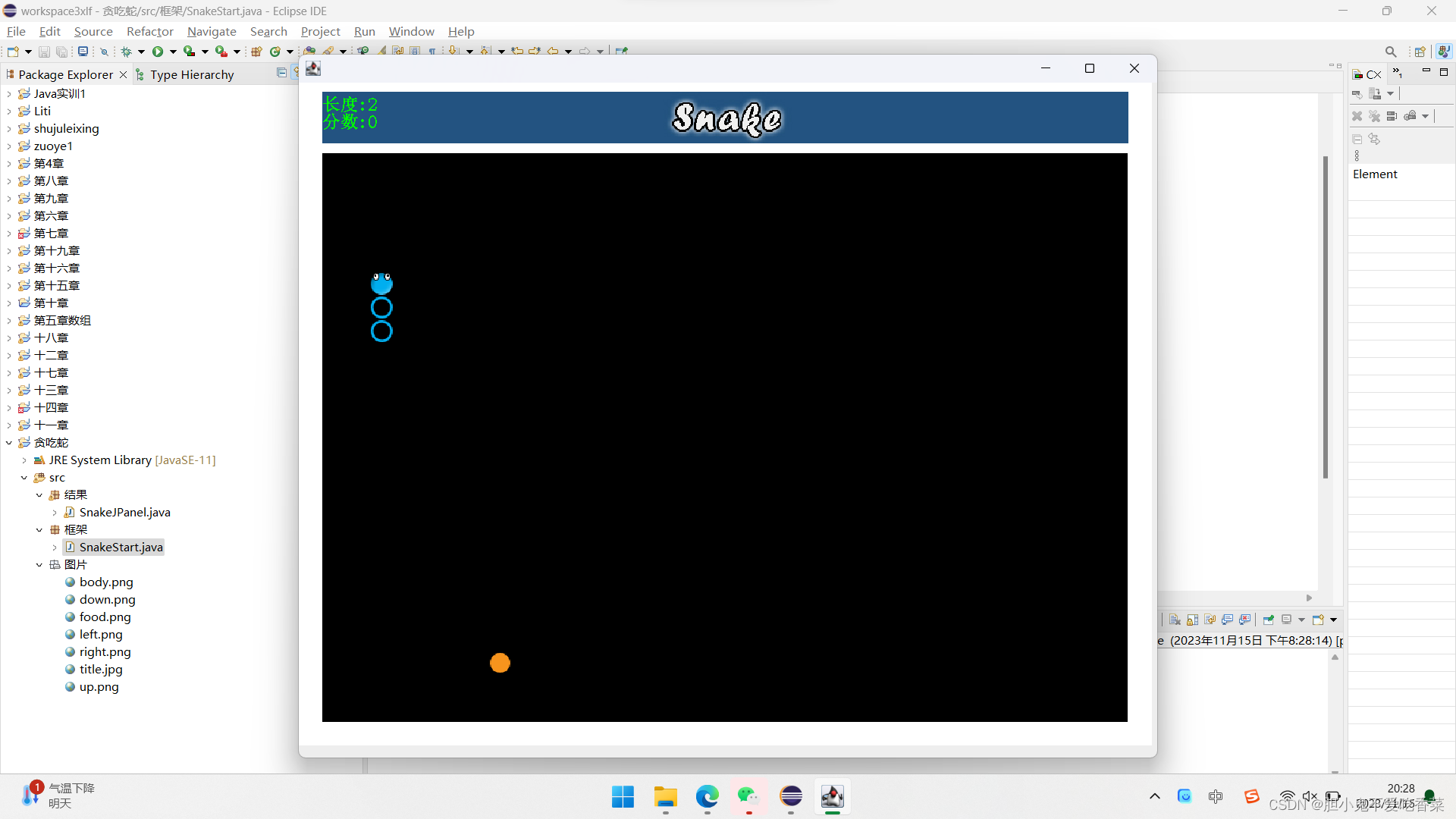
贪吃蛇小游戏代码
框架区 package 结果;import java.awt.Color; import java.awt.EventQueue; import java.awt.Font; import java.awt.Frame; import java.awt.Graphics; import java.awt.Image; import java.util.ArrayList; import java.util.List; import java.util.Random;import javax.s…...
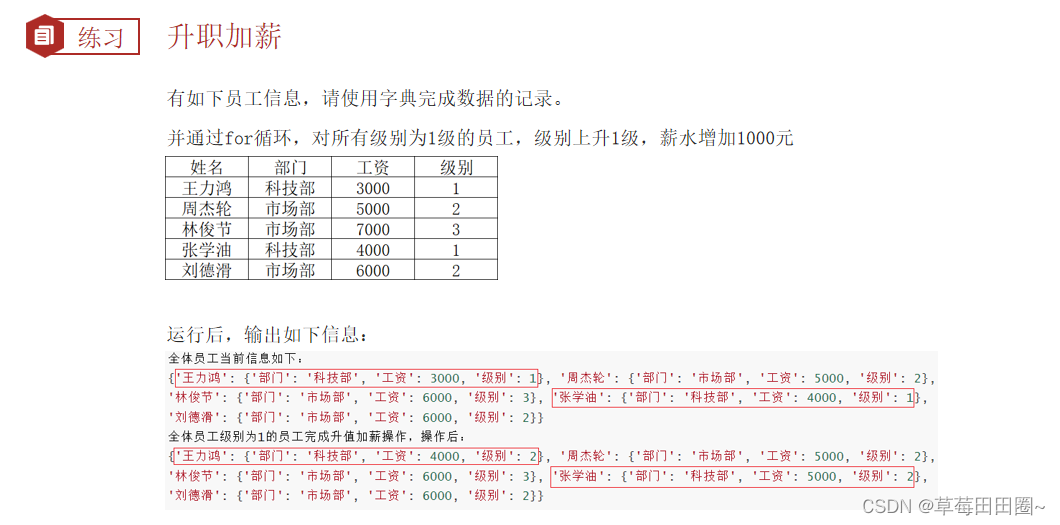
Python数据容器(字典)
字典 1.字典的定义2.字典数据的获取3.字典的嵌套4.嵌套字典的内容获取5.字典的常用操作6.常用操作总结7.遍历字典8.练习 1.字典的定义 同样使用{},不过存储的元素是一个一个的:键值对,语法如下 # 定义字典字面量 {key:value,key:value,...,…...
餐饮展示小程序的作用是什么
餐饮是市场重要的组成部分,尤其是我国八大菜系,各类细分菜数量非常多,并分布在全国,各类大小品牌餐饮商家数量也非常庞大,每个城市的商业街都是一个接一个餐厅,酒类、酒店多样。 餐饮行业经营痛点比较明显…...

33、Flink 的Table API 和 SQL 中的时区
Flink 系列文章 1、Flink 部署、概念介绍、source、transformation、sink使用示例、四大基石介绍和示例等系列综合文章链接 13、Flink 的table api与sql的基本概念、通用api介绍及入门示例 14、Flink 的table api与sql之数据类型: 内置数据类型以及它们的属性 15、Flink 的ta…...

Origin:科研绘图与学术图表绘制从入门到精通
文章目录 一、引言二、安装和启动Origin三、创建和保存图表四、深入学习Origin绘图功能五、应用Origin进行科研绘图和学术图表绘制六、总结与建议《Origin科研绘图与学术图表绘制从入门到精通》亮点内容简介作者简介目录获取方式 一、引言 Origin是一款功能强大的数据分析和科…...

腾讯云标准型SA4服务器AMD处理器性能测评
腾讯云服务器标准型SA4实例CPU采用AMD处理器,新一代腾讯云自研星星海双路服务器,搭配AMD EPYC Genoa处理器,内存采用最新 DDR5,默认网络优化,最高内网收发能力达4500万pps,最高内网带宽可支持100Gbps。阿腾…...
)
LeetCode 2656. K 个元素的最大和:一次遍历(附Python一行版代码)
【LetMeFly】2656.K 个元素的最大和:一次遍历(附Python一行版代码) 力扣题目链接:https://leetcode.cn/problems/maximum-sum-with-exactly-k-elements/ 给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。你需要执行以下操…...

element-ui中Form表单使用自定义验证规则
data() {const validatePass (rule, value, callback) > {if (value.length < 3) {callback(new Error("密码不能小于3位"));} else {callback();}};return {rules: {password: [{ required: true, trigger: "blur", validator: validatePass },]}}…...

android源码添加adb host支持
本文开始参考在 android 上使用 adb client-CSDN博客,在shell中已经可以使用。但当我想在app中用 String command "/data/local/tmp/adb -s 307ef90dc8128844 shell ls";StringBuilder output new StringBuilder();try {Process process Runtime.getR…...

学习c#的第二天
目录 C# 基本语法 using 关键字 class 关键字 C# 中的注释 成员变量 成员函数 类的实例化 标识符 C# 关键字 C# 基本语法 C# 是一种面向对象的编程语言。在面向对象的程序设计方法中,程序由各种相互交互的对象组成。相同种类的对象通常具有相同的类型&…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
