最优化基础(一)
最优化基础(一)1
最优化问题的数学模型
通俗地说,所谓最优化问题,就是求一个多元函数在某个给定集合上的极值. 几乎所有类型的最优化问题都可以用下面的数学模型来描述:
m i n f ( x ) s . t . x ∈ Ω min\ f({x})\\ s.t. \ {x}\in \Omega min f(x)s.t. x∈Ω
这里, Ω \Omega Ω是某个给定的集合(称为可行集或可行域), f ( x ) f(\mathbf{x}) f(x)是定义在集合 Ω \Omega Ω上的实值函数,称为目标函数. 此外,在以上模型中, x = ( x 1 , x 2 , ⋯ , x n ) T x=(x_1,x_2,\cdots,x_n)^T x=(x1,x2,⋯,xn)T通常称为决策变量, s.t. 是subject to (受限于) 的缩写.
人们通常按照可行集的性质对最优化问题进行一个大致的分类:
- 线性规划和非线性规划. — 可行集是有限维空间中的一个子集;
- 组合优化或网络规划. — 可行集中的元素是有限的;
- 动态规划. — 可行集是一个依赖时间的决策序列;
- 最优控制. — 可行集是无穷维空间中的一个连续子集.
在工程设计中有着重要应用的非线性规划,其数学模型为
m i n f ( x ) s . t . h i ( x ) = 0 , i = 1 , ⋯ , l , g i ( x ) ≥ 0 , i = 1 , ⋯ , m , \begin{aligned} &min& & f(x)\\ &s.t. && h_i(x)=0,\ i=1,\cdots,l,\\ &&&g_i(x)\geq0,\ i=1,\cdots,m, \end{aligned} mins.t.f(x)hi(x)=0, i=1,⋯,l,gi(x)≥0, i=1,⋯,m,
其中, f ( x ) , h i ( x ) , g i ( x ) f(x),h_i(x),g_i(x) f(x),hi(x),gi(x)都是定义在 R n \mathbb{R}^n Rn上连续可微的多元实值函数, 且至少有一个是非线性的. 记
E = { i : h i ( x ) = 0 } , I = { i : h i ( x ) ≥ 0 } E=\{i:h_i(x)=0\},\ I=\{i:h_i(x)\geq0\} E={i:hi(x)=0}, I={i:hi(x)≥0}
若指标集$E\cup I=\emptyset $称之为无约束优化问题,否则称为约束优化问题.
此外,通常把目标函数为二次函数而约束函数都是线性函数的优化问题称为二次规划;而目标函数和约束函数都是线性函数的优化问题称为线性规划.
马昌凤. 最优化方法及其Matlab程序设计[M]. 科学出版社, 2010. ↩︎
相关文章:
)
最优化基础(一)
最优化基础(一)1 最优化问题的数学模型 通俗地说,所谓最优化问题,就是求一个多元函数在某个给定集合上的极值. 几乎所有类型的最优化问题都可以用下面的数学模型来描述: m i n f ( x ) s . t . x ∈ Ω min\ f({x})\\ s.t. \ {…...

基于JavaWeb+SpringBoot+Vue医疗器械商城微信小程序系统的设计和实现
基于JavaWebSpringBootVue医疗器械商城微信小程序系统的设计和实现 源码获取入口前言主要技术系统设计功能截图Lun文目录订阅经典源码专栏Java项目精品实战案例《500套》 源码获取 源码获取入口 前言 摘 要 目前医疗器械行业作为医药行业的一个分支,发展十分迅速。…...

java程序中为什么经常使用tomcat
该疑问的产生场景: 原来接触的ssm项目需要在项目配置中设置tomcat,至于为什么要设置tomcat不清楚,只了解需要配置tomcat后项目才能启动。接触的springboot在项目配置中不需要配置tomcat,原因是springboot框架内置了tomcat…...

大带宽服务器需要选择哪些节点
选择大带宽服务器节点需要考虑以下几个因素: 地理位置:选择距离用户较近的节点,可以降低延迟,提高响应速度。 网络质量:大带宽服务器节点应该有良好的网络质量,稳定可靠,能够提供高速的网络传输…...
)
CSS 属性学习笔记(入门)
1. 选择器 CSS选择器用于选择要样式化的HTML元素。以下是一些常见的选择器: 元素选择器 p {color: blue; }描述: 选择所有 <p> 元素,并将文本颜色设置为蓝色。 类选择器 .highlight {background-color: yellow; }描述:…...

[Android]使用View Binding 替代findViewById
1.配置 build.gradle文件中添加配置,然后同步。 android {...buildFeatures {viewBinding true} } 2.用 View Binding 类来访问布局中的视图 在Activity代码的顶部导入生成的 View Binding 类: import com.example.yourapp.databinding.ActivityMai…...

Pytest UI自动化测试实战实例
环境准备 序号库/插件/工具安装命令1确保您已经安装了python3.x2配置python3pycharmselenium2开发环境3安装pytest库 pip install pytest 4安装pytest -html 报告插件pip install pytest-html5安装pypiwin32库(用来模拟按键)pip install pypiwin32 6安装openpyxl解析excel文…...

软件测试/测试开发丨接口自动化测试学习笔记,多环境自动切换
点此获取更多相关资料 本文为霍格沃兹测试开发学社学员学习笔记分享 原文链接:https://ceshiren.com/t/topic/28026 多环境介绍 环境使用场景备注dev开发环境开发自测QA测试环境QA日常测试preprod预发布环境回归测试、产品验测试prod线上环境用户使用的环境 通过环…...

Spring-IoC与DI入门案例
IoC入门案例 IoC入门案例思路分析 管理什么?(Service与Dao)如何将被管理的对象告知IoC容器?(配置)被管理的对象交给IoC容器,如何获取到IoC容器?(接口)IoC容…...
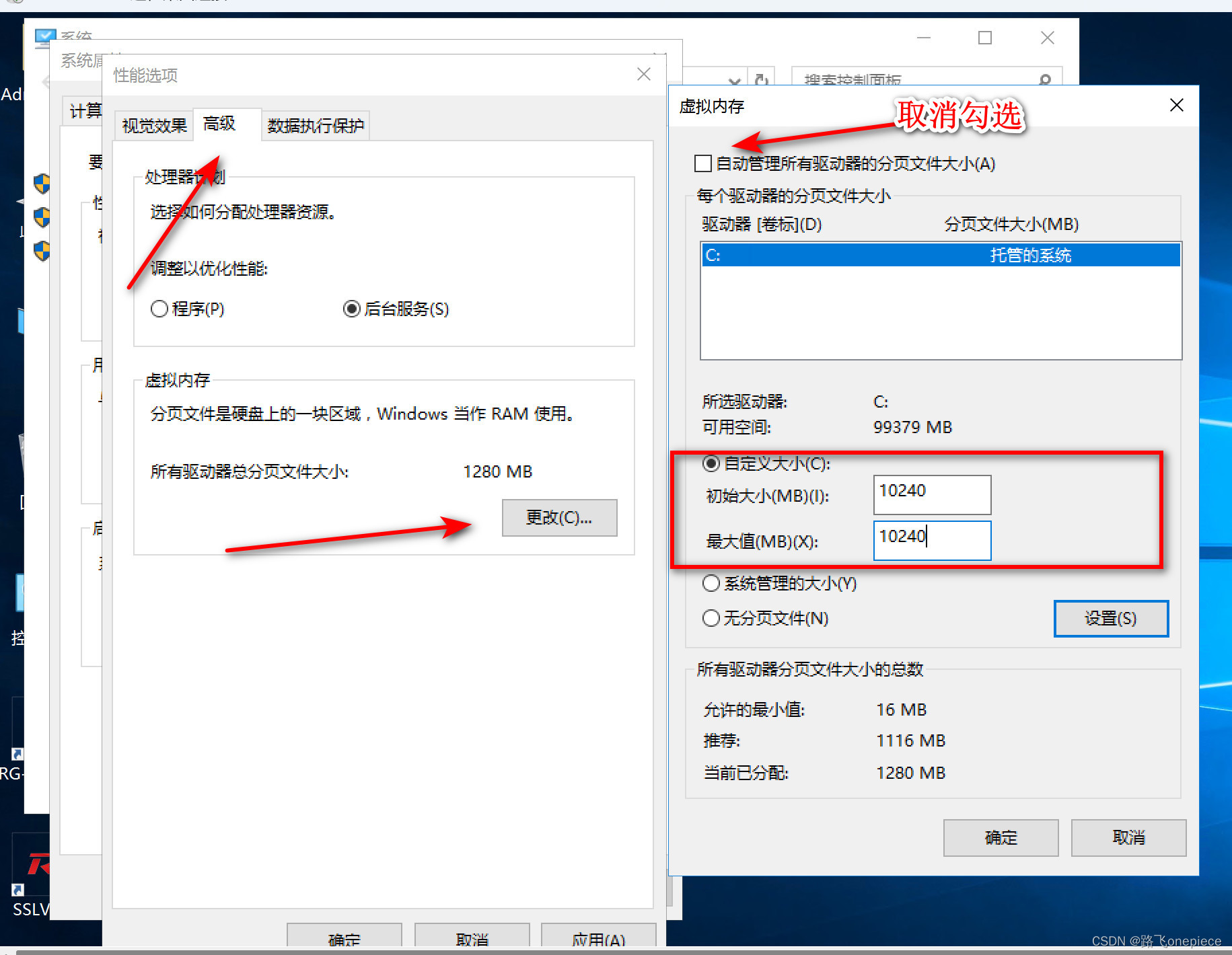
windows虚拟内存自定义分配以及mysql错误:Row size too large (> 8126)
文章目录 虚拟内存概要windows-server配置虚拟内存技术名词解释关于mysql错误Row size too large (> 8126)问题分析解决办法 虚拟内存概要 虚拟内存别称虚拟存储器(Virtual Memory)。电脑中所运行的程序均需经由内存执行,若执行的程序占用…...

自动备份pgsql数据库
bat文件中的内容: PATH D:\Program Files\PostgreSQL\13\bin;D:\Program Files\7-Zip set PGPASSWORD**** pg_dump -h 8.134.151.187 -p 5466 -U sky -d mip_db --schema-only -f D:\DB\backup\%TODAY%-schema-mip_db_ali.sql pg_dump -h 8.134.151.187 -p 5466…...

networkx使用draw画图报错:TypeError: ‘_AxesStack‘ object is not callable
一、问题描述 在使用networkx的draw绘图时nx.draw(g,posnx.spring_layout(g)),报错:TypeError: _AxesStack object is not callable 二、原因 可能是当前python环境下的networkx和matplotlib的版本不匹配。我报错时的networkx2.8,matplotl…...

tcpdump 常用命令
wireshark抓包抓取服务器10.20.1.101上的包,使用网络接口wlan ./tcpdump -vvv host 192.168.137.142 and 10.20.1.101 and ! port 23 -w rtmp.cap ./tcpdump -vvv host port 9013 -w ppt.cap...

Linux 下安装 Maven 3.8.8【详细步骤】
前提条件:安装 jdk,详见 安装jdk1.8 # 下载(地址可能会因为版本更新无效,到时候直接去官网找下载地址) wget https://dlcdn.apache.org/maven/maven-3/3.8.8/binaries/apache-maven-3.8.8-bin.tar.gz# 解压 tar -zxvf apache-maven-3.8.8-bin.tar.gz# 修改环境变量 vi /e…...
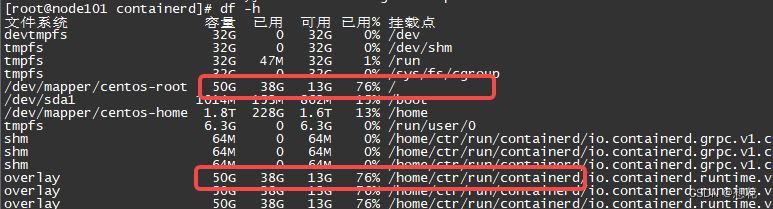
报错资源不足,k8s使用containerd运行容器修改挂载点根目录换成/home
运行k8s一段时间发现存储不足报错 发现这里用的是根路径的挂载,修改一下...

JS代码其实可以这样写
给大家推荐一个实用面试题库 1、前端面试题库 (面试必备) 推荐:★★★★★ 地址:web前端面试题库 日常工作中,我确实经常去帮大家review代码,长期以来,我发现有些个功能函数,JS其实可以稍微调整一下,或者换个方式来处理,代码就会看起来更清晰,更简洁,…...

day14-文件系统工作流程分析
1.内核启动文件系统后,文件系统的工作流程 1.参数的接收 2.参数的解析 3.参数的应用 问题: 1. UBOOT 传给 KERNEL 的参数是以tagglist进行的 KERNEL 传给 文件系统(busybox)的参数是以什么进行的? 2. 在整个文件系统中都需…...

kubectl 常用命令搜集 —— 筑梦之路
集群信息: 1. 显示 Kubernetes 版本:kubectl version 2. 显示集群信息:kubectl cluster-info 3. 列出集群中的所有节点:kubectl get nodes 4. 查看一个具体的节点详情:kubectl describe node <node-name> 5.…...

计算3D目标框的NMS
3D障碍物目标框(中心点坐标XYZ、长宽高lwh、朝向角theta)的非极大值抑制 #include <iostream> #include <vector> #include <algorithm> #include <opencv2/opencv.hpp>// 定义3D目标框的结构体 struct BoundingBox3D {double …...
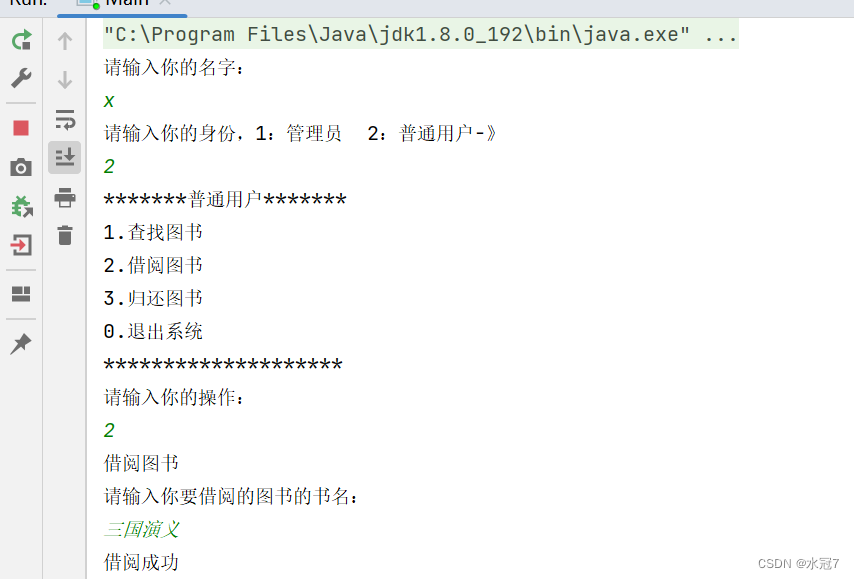
【Java实现图书管理系统】
图书管理系统 1. 设计背景2. 设计思路3. 模块展示代码演示3.1 Book类3.2 BookList类(书架类)3.4 用户类 - User类3.5 子类管理员类 -- AdminUser类3.6 子类普通用户类 -- NormalUser类3.7 操作接口3.8 操作类3.8.1 查找操作 -- FindOperation类3.8.2 增加…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
