CSDN每日一题学习训练——Python版(简化路径,不同的二叉搜索树)
版本说明
当前版本号[20231116]。
| 版本 | 修改说明 |
|---|---|
| 20231116 | 初版 |
目录
文章目录
- 版本说明
- 目录
- 简化路径
- 题目
- 解题思路
- 代码思路
- 参考代码
- 不同的二叉搜索树
- 题目
- 解题思路
- 代码思路
- 参考代码
简化路径
题目
给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 ‘/’ 开头),请你将其转化为更加简洁的规范路径。
在 Unix 风格的文件系统中,一个点(.)表示当前目录本身;此外,两个点 (…) 表示将目录切换到上一级(指向父目录);两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠(即,‘//’)都被视为单个斜杠 ‘/’ 。 对于此问题,任何其他格式的点(例如,‘…’)均被视为文件/目录名称。
请注意,返回的 规范路径 必须遵循下述格式:
始终以斜杠 ‘/’ 开头。
两个目录名之间必须只有一个斜杠 ‘/’ 。
最后一个目录名(如果存在)不能 以 ‘/’ 结尾。
此外,路径仅包含从根目录到目标文件或目录的路径上的目录(即,不含 ‘.’ 或 ‘…’)。
返回简化后得到的 规范路径 。
示例 1:
输入:path = “/home/”
输出:“/home”
解释:注意,最后一个目录名后面没有斜杠。
示例 2:
输入:path = “/…/”
输出:“/”
解释:从根目录向上一级是不可行的,因为根目录是你可以到达的最高级。
示例 3:
输入:path = “/home//foo/”
输出:“/home/foo”
解释:在规范路径中,多个连续斜杠需要用一个斜杠替换。
示例 4:
输入:path = “/a/./b/…/…/c/”
输出:“/c”
提示:
1 <= path.length <= 3000
path 由英文字母,数字,‘.’,‘/’ 或 ‘_’ 组成。
path 是一个有效的 Unix 风格绝对路径。
解题思路
解题思路:
- 创建一个空列表 result,用于存储简化后的路径。
- 将输入的路径字符串 path 按照斜杠 ‘/’ 进行分割,得到一个列表 plist。
- 遍历 plist 中的每个元素 pos。
- 如果 pos 不为空,则进行以下判断:
- 如果 pos 等于 ‘…’,表示需要返回上一级目录。尝试从 result 中弹出最后一个元素(即返回上一级目录)。如果 result 为空,则将其重置为空列表。
- 如果 pos 不等于 ‘.’,表示当前目录或文件名有效。将其添加到 result 列表中。
- 如果 pos 不为空,则进行以下判断:
- 使用 join() 方法将 result 列表中的元素用斜杠 ‘/’ 连接起来,并在前面加上一个斜杠作为根目录。
- 返回简化后的规范路径。
代码思路
-
先定义了一个名为
Solution的类,并在其中实现了一个名为simplifyPath的方法。该方法接受一个字符串类型的参数path,表示要简化的文件路径。def simplifyPath(self, path): -
在方法内部,首先定义了一个空列表
result,用于存储简化后的路径。然后,使用split('/')方法将输入的路径按照斜杠分割成一个列表plist,其中每个元素表示路径中的一个目录或文件名。result = [] # 初始化结果列表plist = path.split('/') # 将路径按照斜杠分割成列表 -
接下来,使用一个循环遍历
plist中的每个元素。如果当前元素不为空,则进行以下判断: -
-
如果当前元素为
..,表示需要返回上一级目录。此时,尝试从result中弹出最后一个元素(即返回上一级目录)。如果result为空,则将其重置为空列表。for pos in plist: # 遍历列表中的每个元素if pos: # 如果元素不为空if pos == '..': # 如果元素为'..',表示返回上一级目录try:result.pop() # 弹出结果列表中最后一个元素except:result = [] # 如果结果列表为空,则将其重置为空列表 -
如果当前元素不为
.,表示当前目录或文件名有效。将其添加到result列表中。elif pos != '.': # 如果元素不为'.',表示当前目录result.append(pos) # 将当前目录添加到结果列表中
-
-
最后,使用
join()方法将result列表中的元素用斜杠连接起来,并在前面加上一个斜杠作为根目录。最终返回简化后的路径。return '/' + '/'.join(result) # 将结果列表中的元素用斜杠连接起来,并在前面加上一个斜杠作为根目录 -
在代码的最后,创建了一个
Solution类的实例s,并调用其simplifyPath方法,传入一个示例路径/home/,并将结果打印输出。
s = Solution() # 创建Solution类的实例
print(s.simplifyPath(path="/home/")) # 调用simplifyPath方法,传入路径参数,并打印结果
参考代码
这段代码主要是使用栈来处理路径中的目录和文件名。
class Solution(object):def simplifyPath(self, path):""":type path: str:rtype: str"""result = []plist = path.split('/')for pos in plist:if pos:if pos == '..':try:result.pop()except:result = []elif pos != '.':result.append(pos)return '/'+'/'.join(result)
# %%
s = Solution()
print(s.simplifyPath(path = "/home/"))
不同的二叉搜索树
题目
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
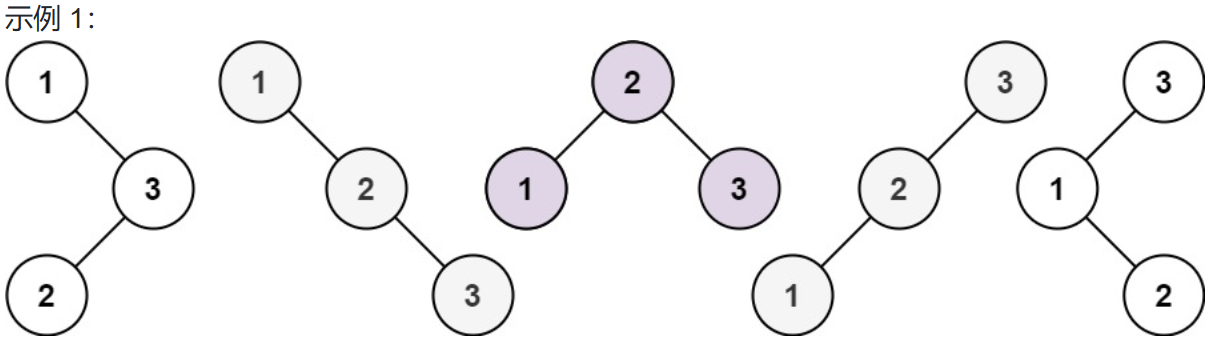
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
提示:
1 <= n <= 19
解题思路
-
这个问题可以使用动态规划来解决。我们可以定义一个数组dp,其中dp[i]表示由i个节点组成的二叉搜索树的种数。根据题目要求,我们可以得到以下状态转移方程:
dp[i] = Σ(dp[j-1] * dp[i-j]) (j=1,2,...,i) -
这个方程的含义是,对于每个节点i,它有左子树和右子树,左子树的节点数为j-1,右子树的节点数为i-j。因此,我们需要遍历所有可能的j值,计算出对应的二叉搜索树的种数,并将它们累加起来。
代码思路
-
初始化一个长度为n+1的动态规划数组dp,初始值为0。
# 初始化动态规划数组,长度为n+1,初始值为0dp = [0] * (n + 1) -
当节点数为0时,只有一种可能,即空树,所以将dp[0]设为1。
-
当节点数为1时,只有一种可能,即只有一个节点的树,所以将dp[1]设为1。
# 当节点数为0时,只有一种可能,即空树dp[0] = 1# 当节点数为1时,只有一种可能,即只有一个节点的树dp[1] = 1 -
从第2个节点开始遍历到第n个节点,对于每个节点level,遍历所有可能的根节点root。
# 从第2个节点开始遍历到第n个节点for level in range(2, n + 1):# 对于每个节点,遍历所有可能的根节点for root in range(1, level + 1): -
根据组合数公式,计算当前节点数下,以root为根节点的二叉搜索树的数量。具体计算公式为:dp[level] += dp[level - root] * dp[root - 1]。
# 根据组合数公式,计算当前节点数下,以root为根节点的二叉搜索树的数量dp[level] += dp[level - root] * dp[root - 1] -
返回给定节点数下的二叉搜索树数量,即dp[n]。
# 返回给定节点数下的二叉搜索树数量return dp[n] -
创建Solution对象s,并调用numTrees方法,传入节点数n=3,计算节点数为3的二叉搜索树数量,并打印结果。
# 创建Solution对象
s = Solution()
# 调用numTrees方法,计算节点数为3的二叉搜索树数量,并打印结果
print(s.numTrees(n = 3))参考代码
这段代码是一个计算给定节点数的二叉搜索树数量的函数。它使用了动态规划的方法,通过遍历每个节点和所有可能的根节点,计算出以当前节点为根节点的二叉搜索树的数量。最后返回给定节点数下的二叉搜索树数量。
class Solution(object):def numTrees(self, n):""":type n: int:rtype: int"""dp = [0] * (n + 1)dp[0] = 1dp[1] = 1for level in range(2, n + 1):for root in range(1, level + 1):dp[level] += dp[level - root] * dp[root - 1]return dp[n]
# %%
s = Solution()
print(s.numTrees(n = 3))
相关文章:

CSDN每日一题学习训练——Python版(简化路径,不同的二叉搜索树)
版本说明 当前版本号[20231116]。 版本修改说明20231116初版 目录 文章目录 版本说明目录简化路径题目解题思路代码思路参考代码 不同的二叉搜索树题目解题思路代码思路参考代码 简化路径 题目 给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路…...

milvus集合管理
一、创建集合 集合由一个或多个分区组成。在创建新集合时,Milvus会创建一个默认分区_default 1.准备模式 需要创建的集合必须包含一个主键字段和一个向量字段。INT64和String是主键字段支持的数据类型。 首先,准备必要的参数,包括字段模式、…...
基于SSM的教学管理系统设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...
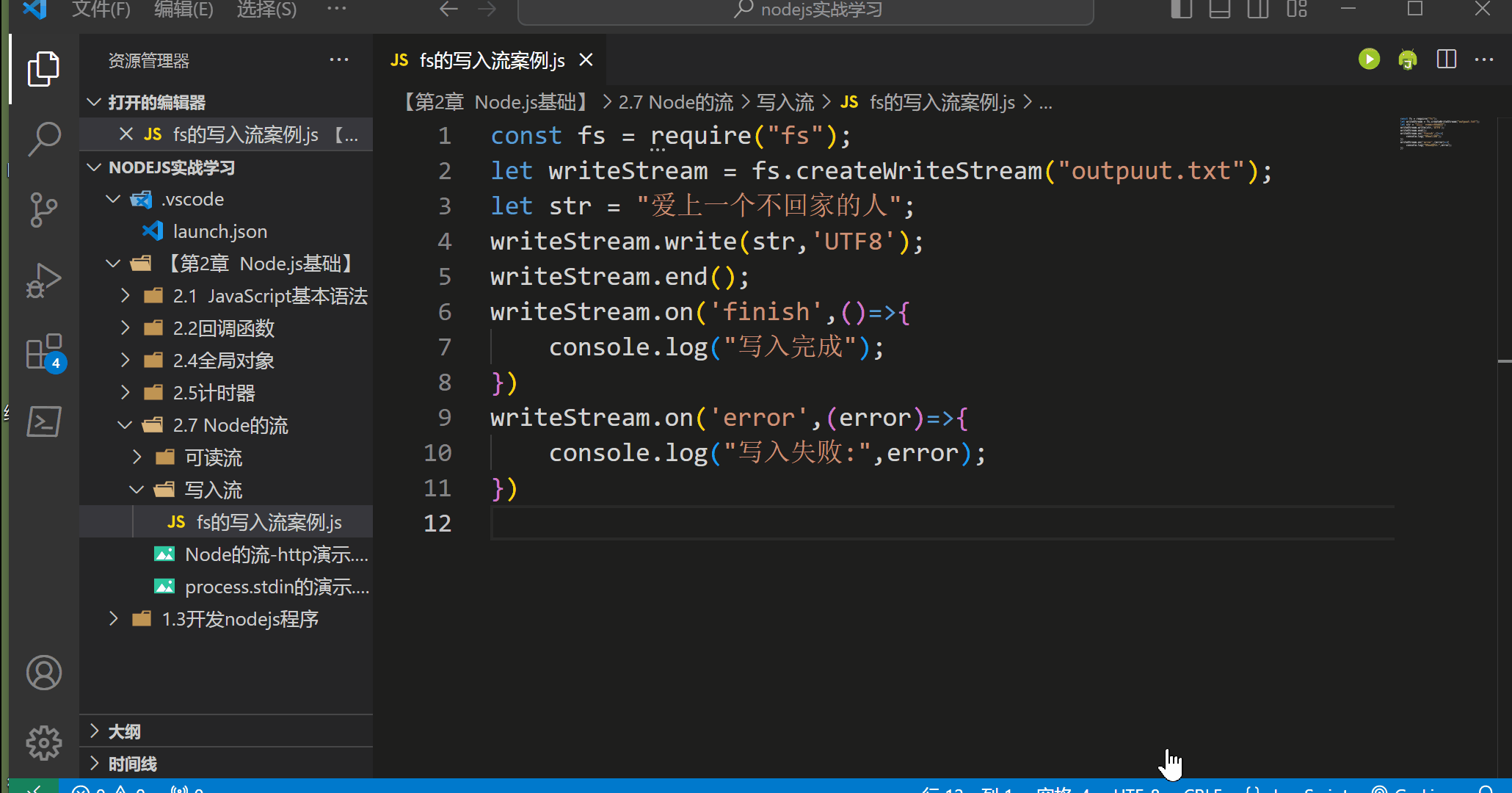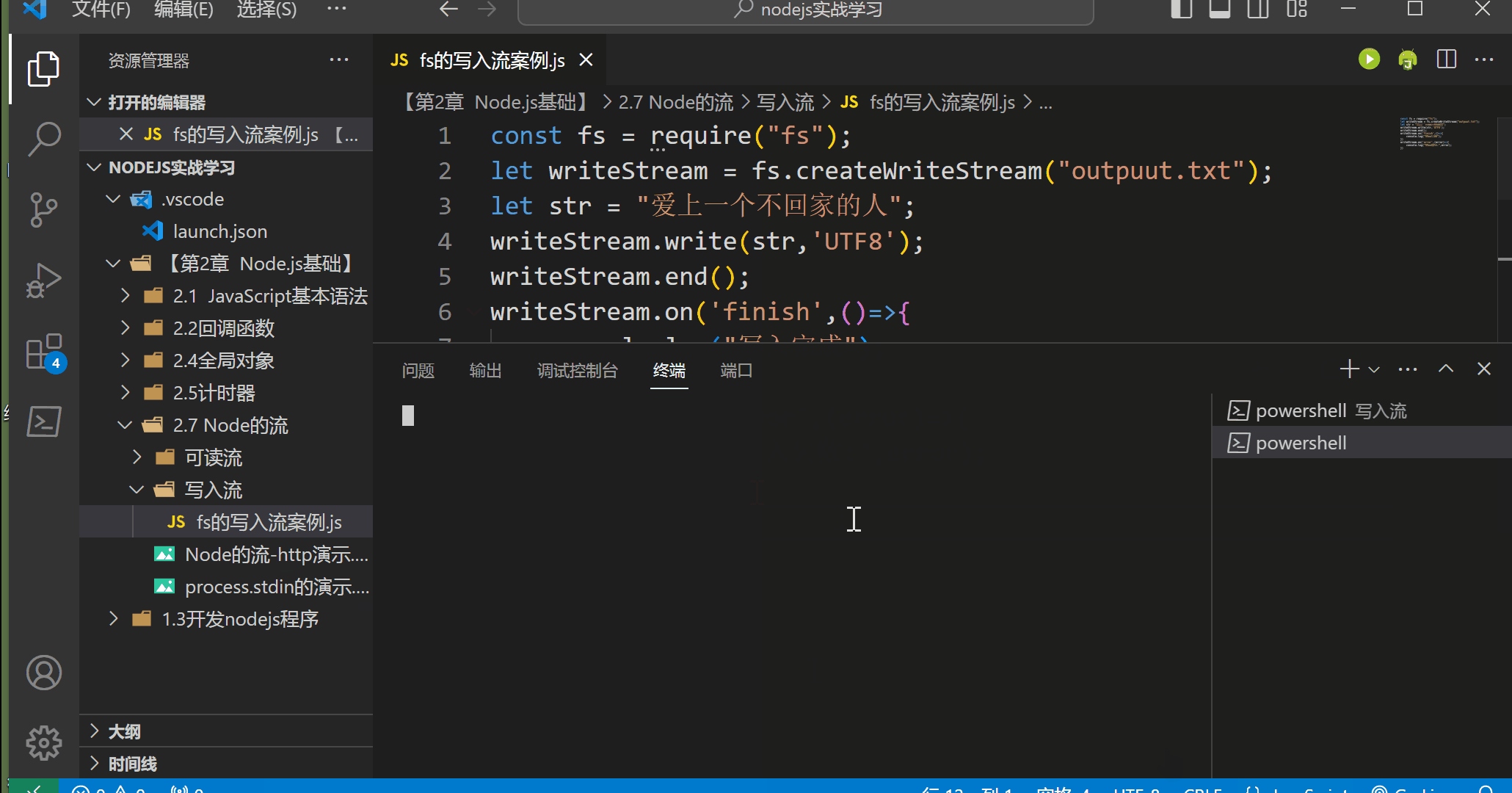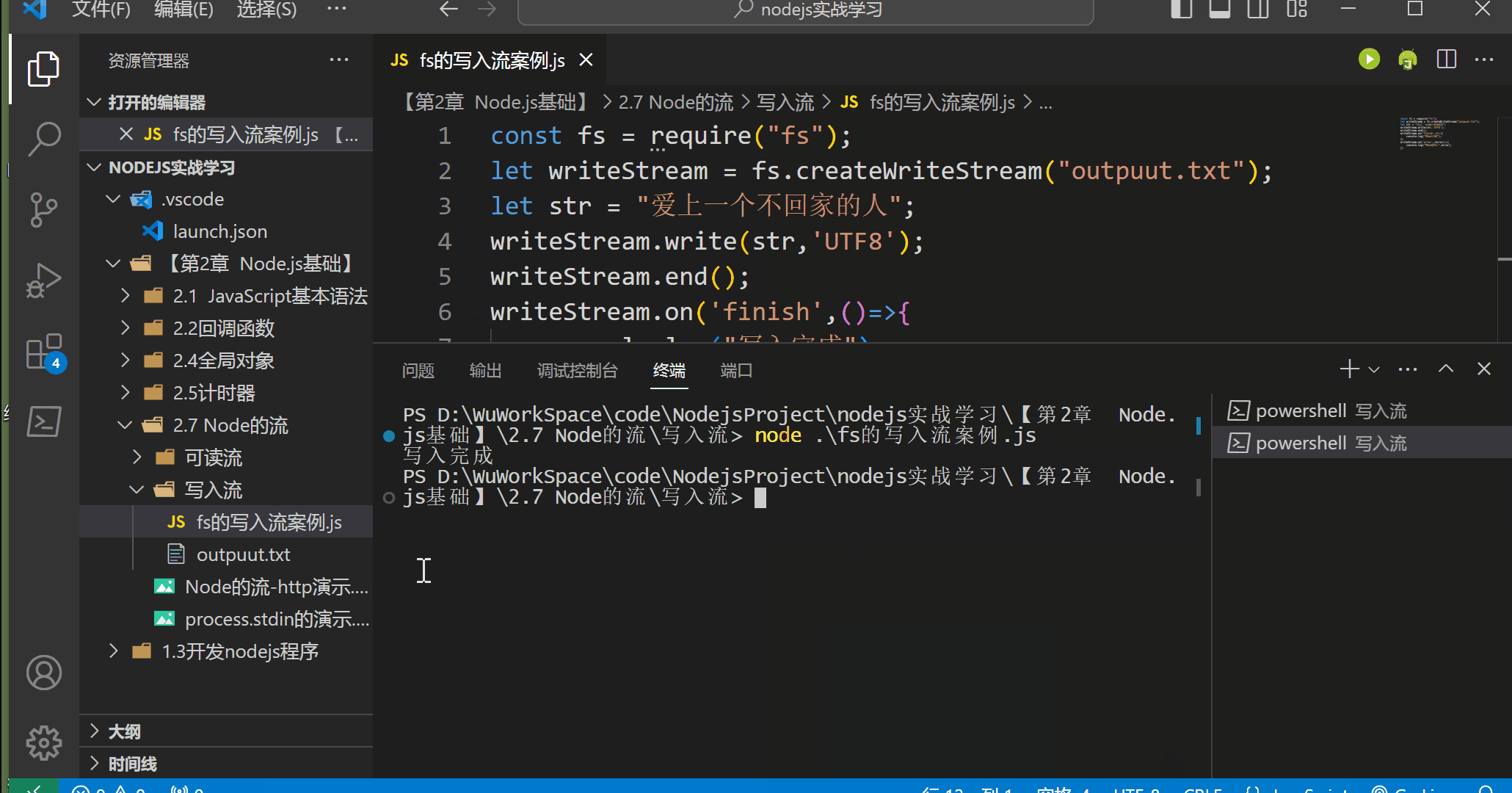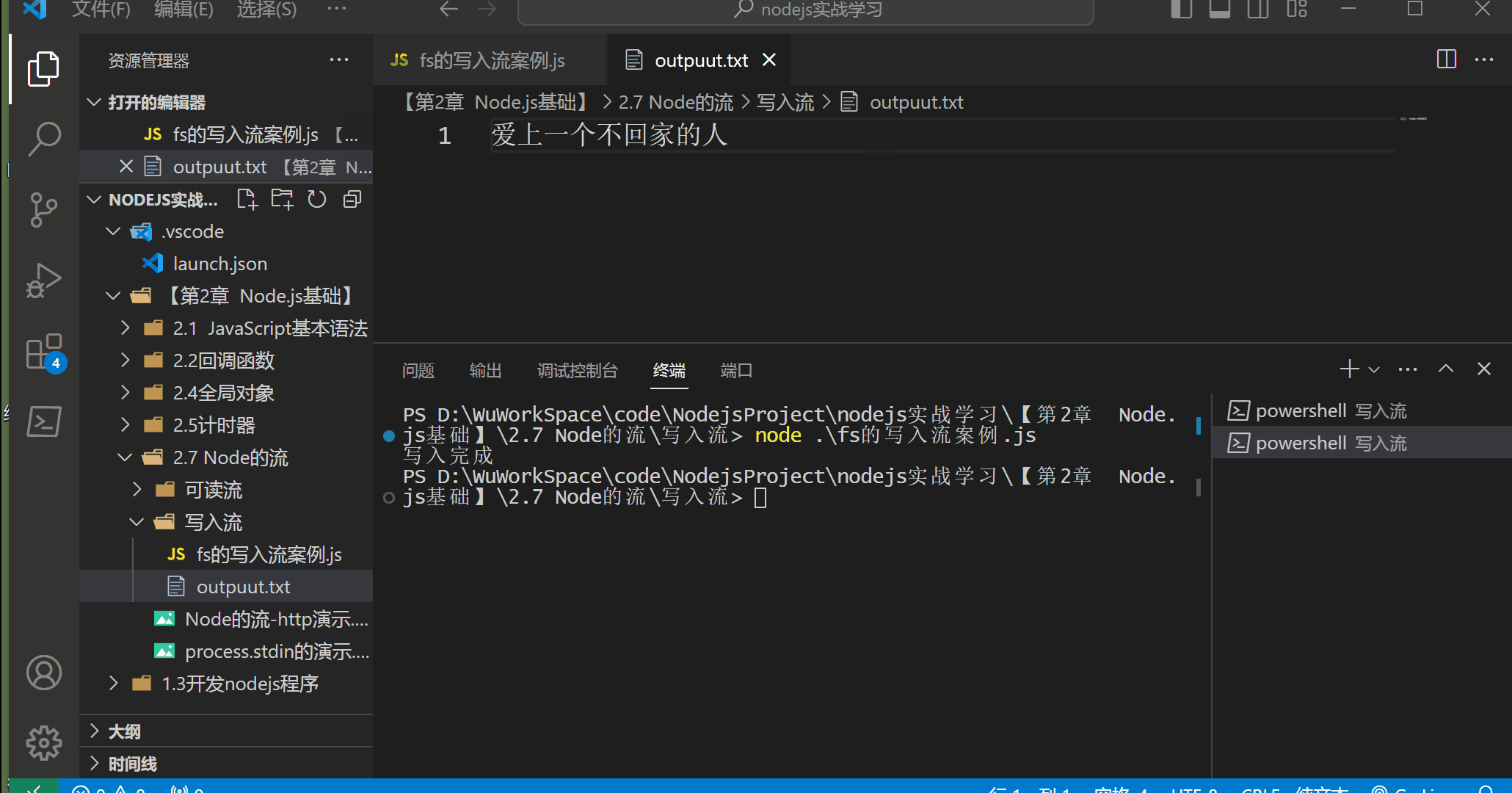
【第2章 Node.js基础】2.7 Node.js 的流(一)可写流
🌈可写流 🚀什么是可写流 可写流是对数据被写入的目的地的一种抽象。 所有可写流都实现了 stream.Writable类定义的接口。 可写流的例子包括,也都是实现了可写流接口的双工流 客户端的 HTTP 请求、服务器的HTTP 响应、fs 的写入流、zlib…...
【kerberos】使用 curl 访问受 Kerberos HTTP SPNEGO 保护的 URL
前言: 大数据集群集成 Kerberos 后,很多 WEBUI 打开都会提示输入用户名和密码。由于我想获取 flink 任务的详情,且KNOX 并不支持Flink api,查看KNOX 直接的列表:https://docs.cloudera.com/cdp-private-cloud-base/7.…...
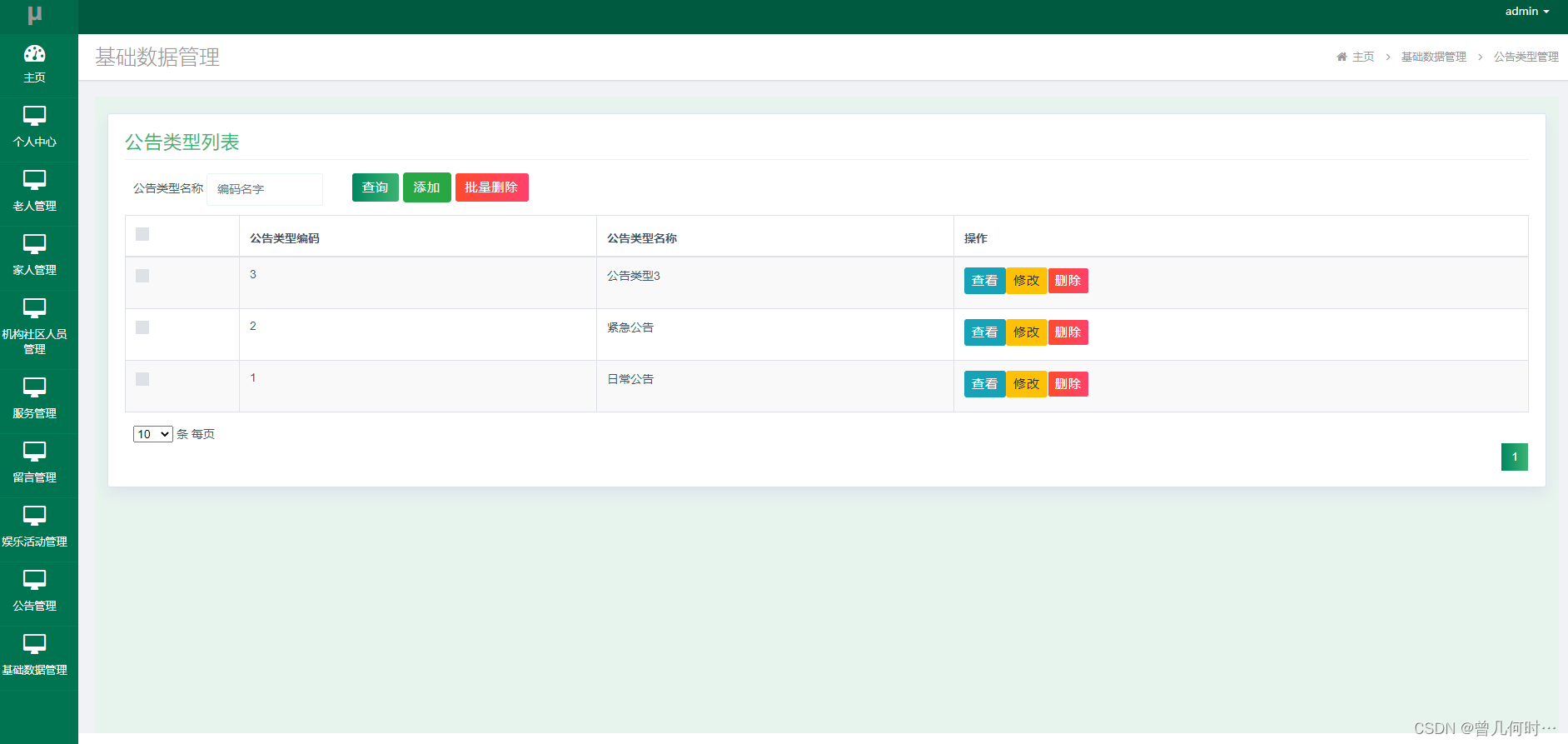
基于SSM的智慧养老平台设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...
图像生成colab集合
不过colab会做检测,一般文生图算法是基本很难跑起来的。 https://github.com/camenduruhttps://github.com/camenduru这哥们有很多colab。 1.stable-diffusion-webui https://colab.research.google.com/drive/1Iy-xW9t1-OQWhb0hNxueGij8phCyluOh#scrollTow3KNZ-…...
SpringBoot整合Quartz示例
数据表 加不加无所谓,如果需要重启服务器后重新执行所有JOB就把sql加上 如果不加表 将application.properties中的quartz数据库配置去掉 自己执行自己的逻辑来就好,大不了每次启动之后重新加载自己的逻辑 链接:https://pan.baidu.com/s/1KqOPYMfI4eHcEMxt5Bmt…...

物联网AI MicroPython学习之语法 I2C总线
学物联网,来万物简单IoT物联网!! I2C 介绍 模块功能: I2C Master设备驱动 接口说明 I2C - 构建硬件I2C对象 函数原型:I2C(id, scl, sda, freq)参数说明: 参数类型必选参数?说明idintYI2C外设ÿ…...

RocketMQ的适用场景有哪些?
程序员的公众号:源1024,获取更多资料,无加密无套路! 最近整理了一波电子书籍资料,包含《Effective Java中文版 第2版》《深入JAVA虚拟机》,《重构改善既有代码设计》,《MySQL高性能-第3版》&…...

ubuntu启动转圈,无法进入登录界面
安装卸载搜狗拼音输入法相关东西后出现启动转圈问题 当前使用的是lightdm,按网上说去切换成gdm3 (1)要在刚进入系统没显示圈圈和ubuntu时长按shift进入gurb。 (2)选择Ubuntu高级选项,enter (3)…...
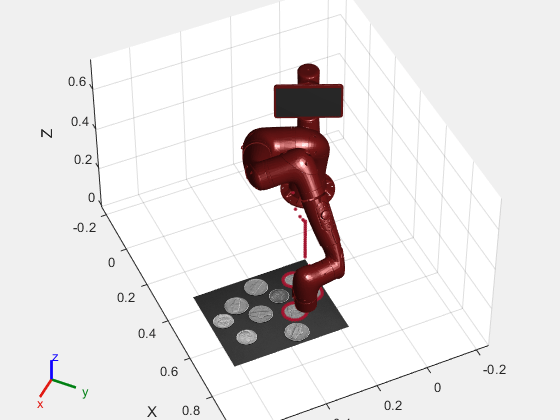
MATLAB 机械臂逆运动学进行轨迹控制建模
系列文章目录 文章目录 系列文章目录前言一、模型概览1.1 Target Pose Generation 目标姿势生成1.2 Inverse Kinematics 逆运动学1.3 Manipulator Dynamics 机械手动力学1.4 Pose Measurement 姿势测量 二、机械手定义三、生成航点四、模型设置五、模拟机械手运动六、将结果可视…...

【计算机组成原理】定点加法、减法运算
系列文章目录 绘制出纯整数(1字节)和纯小数的数轴 将十进制数20.59375,转换成754标准的32位浮点数的二进制存储格式 用双符号位补码求 x 0.1010011, y -0.1001010, 分别求出 x y, x - y,并判溢出...

scp 跨服务器传输命令,把一个服务器上的文件复制传到当前服务器目录下
要将一个服务器上的文件复制到当前服务器的目录下,可以使用 scp 命令进行跨服务器传输。以下是具体的命令格式: 复制 scp usernamesource_server:/path/to/source_file destination_directory username: 远程服务器的用户名。 source_server: 远程服务…...

【python基础】用户输入和while循环详解
文章目录 一. 函数input()的工作原理1. 编写清晰的程序2. 使用int()来获取数值输入3. 求模运算符 二. while循环简介1. 使用while循环2. 让用户选择何时退出3. 使用标志4. 使用break退出循环5. 在循环中使用continue 三. 使用while循环处理列表和字典1. 在列表之间移动元素2. 删…...
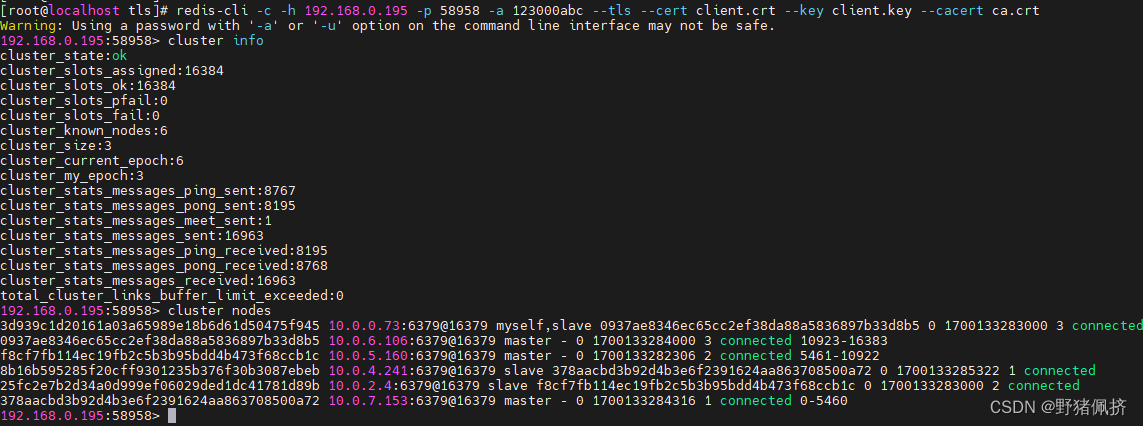
k8s-部署Redis-cluster(TLS)
helm pull bitnami/redis-cluster v8.3.8拉取源码生成证书 git clone https://github.com/redis/redis.git #文档 https://redis.io/docs/management/security/encryption/#getting-started生成你的TLS证书用官网的工具生成 1 Run ./utils/gen-test-certs.sh 生成根CA和服务…...

计算机毕业设计选题推荐-幼儿园管理微信小程序/安卓APP-项目实战
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

ElasticStack日志分析平台-ES 集群、Kibana与Kafka
一、Elasticsearch 1、介绍: Elasticsearch 是一个开源的分布式搜索和分析引擎,Logstash 和 Beats 收集的数据可以存储在 Elasticsearch 中进行搜索和分析。 Elasticsearch为所有类型的数据提供近乎实时的搜索和分析:一旦数据被索引&#…...
微机原理_10
一、单项选择题(本大题共15小题,每小题3分,共45分。在每小题给出的四个备选项中,选出一个正确的答案。) 1,将二进制数110110.01转换为十六进制为() A. 66.1H B. 36.4H C. 66.4 D. 36.2 2,一台计算机的字长是4个字节,含义是() A.能处理的最大…...
第八章:SpringMVC程序开发)
(SpringBoot)第八章:SpringMVC程序开发
文章目录 一:Spring MVC概述(1)什么是Spring MVC(2)什么是MVC(3)Spring MVC和SpringBoot(4)如何学习Spring MVC二:Spring MVC创建和连接(1)Spring MVC项目创建(2)@RequestMapping注解三:Spring MVC处理参数(1)传递简单参数(2)传递对象(3)@RequestParam:重…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...
