解读CRC校验计算
个人随笔 (Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu)
参考:http://www.sunshine2k.de/articles/coding/crc/understanding_crc.html
参考:https://en.wikipedia.org/wiki/Cyclic_redundancy_check
参考:https://www.cnblogs.com/yikoulinux/p/14952297.html
参考:https://crccalc.com/
CRC校验定义:
循环冗余校验码(CRC – Cyclic Redundancy Checksum),简称循环码,是一种常用的、具有检错、纠错能力的校验码,在早期的通信中运用广泛。
循环冗余校验码常用于外存储器和计算机同步通信的数据校验。
A cyclic redundancy check (CRC) is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to digital data.
最简单的错误检验方法,奇偶检验,实际上是一个1bit的CRC,它使用生成多项式x+1(0b11),被成为CRC-1。
The simplest error-detection system, the parity bit, is in fact a 1-bit CRC: it uses the generator polynomial x + 1 (two terms),[3] and has the name CRC-1.
关于CRC校验的理解:
CRC校验的思路是,把一个串作为一个长的数值,附加某段校验码后,形成一个更长的数值串,对该数值串求余运算时能够整除;从而来校验内容未被篡改;
求余运算和每一位的数值都相关,所以校验码会受其每一位修改的影响;
另外,能被整除的概率,和补取的校验码段长度相关,且通常只有一个取值是能整除的,对于1字节校验码来说,概率是1/256,对于4字节校验码来说,概率是1/2^32,校验正确率还是比较高的;
被附加的某段校验码就称之为CRC校验码。
按照这个校验思路,举个10进制的例子:
例如1位校验码,对9求余,1000这个数值校验时,先补全一位0,10000%9,得到值1111,余数1;
如果要整除,就要9-1,补一个8在后面;10008 % 9 可以整除。所以1000后面的CRC校验码就为8。
实际求余的计算,为了提升校验效率,采用的模二除法:
对于模二除法,与算术除法不同的是每一位除的结果不影响其他位,即不向上借位,所以实际上相当于二进制中的逻辑异或运算。
0 mod 1 = 1 --> 0 ^ 1 = 1
1 mod 0 = 1 --> 1 ^ 0 = 1
0 mod 0 = 0 --> 0 ^ 0 = 0
1 mod 1 = 0 --> 1 ^ 1 = 0
另外,模二加法,模二减法与这个规律也一致,也与异或效果一致
0 + 1 = 0 - 1 = 1
1 + 0 = 1 - 0 =1
0 + 0 = 0 - 0 = 0
1 + 1 = 1 - 1 = 0
模二乘法不同,和 按位与& 结果一致 1 * 1 = 1 --> 1 & 1 = 1
对于异或算法来说:满足交换律,三者还能互为求值,非常适合互为计算(ps. 简单加密解密值非常适合)
a ^ b = b ^ a = c
a ^ c = c ^ a = b
b ^ c = c ^ b = a
这样来说,一个串str如果要获得它的CRC校验串,流程就是:
a. 对该串str补二进制0,补0的长度为crc校验码的二进制长度
b. 对补0后的串进行模二除法,获取到余数,余数就是补值 ( 0 ^ a = b --> b ^ a = 0)
c. 把补值放到该串str的后面,作为CRC校验码
对于所使用的除数,多项式规律为:
crc8 常用 x^8 + x^2 + x + 1,首位是比较对齐用,剩余值为 0x07,二进制逆序为 0xE0
crc16 常用 x^16 + x^15 + x^2 + 1,首位是比较对齐用,剩余值为 0x8005,二进制逆序为0xA001
crc32 常用 x^32 + x^26 + x^23 + x^22 + x^16 + x^12 + x^11 + x^10 + x^8 + x^7 + x^5 + x^4 + x^2 + x + 1,首位用于比较对齐,剩余值为 0x04C11DB7,二进制逆序为0xEDB88320
对于CRC的计算简化:
CRC计算时,一般都是使用查表法计算的;
假设一个字符串长度是一个字节,当明确多项式除数之后,那么它的CRC校验值,只可能有256中相对应,也即可以查表得到。
那么对于一个实际字符串来说,可以看作由一个1字节串,1字节串连接组成的长串;
计算时:
a. 把第一个字节的crc值获取到之后,带入到下一个字节的计算中;
b. 把crc首个字节与当前字节合并,合成值查表,获取到一个新的crc值,再把上一个crc的剩余字节移位后合并到crc新值上,得到合并后的值;
c. 依次类推,等到字符串末尾时,就获取到了最终的crc值;
CRC参数:
CRC的关键必选的参数是width和polynomial;CRC校验宽度width,例如8字节,16字节,32字节,标识了产生CRC校验值的位宽;CRC多项式polynomial,例如crc8常用的 x8+x2+x+1,是crc校验所使用的除数。
除了关键必选参数外,crc扩展出了initVal初始值,xorValue结果xor值,refect-in输入值位镜像, refect-out输出值位镜像参数,增加了crc校验计算的复杂度;
综上这些参数的设定,也被分别应用到不同的领域,不同的场景。
8字节的一个例子:
对于8字节的计算,参考如下
unsigned char charcrc8(const unsigned char ch, bool reflect=false){unsigned char crc = ch;if (!reflect){const unsigned char polynomial = 0x07;for (int i=0; i<8; i++){if ((crc & 0x80) != 0)crc = (crc << 1) ^ polynomial;elsecrc <<= 1;}}else{const unsigned char polynomial = 0xE0;for (int i=0; i<8; i++){if ((crc & 0x1) != 0)crc = (crc >> 1) ^ polynomial;elsecrc >>= 1;}}return crc;
}
unsigned char calccrc8(const char* str, int count, unsigned char init = 0, bool reflect=false, unsigned char xorcrc = 0){unsigned char crc = init;for (int i=0; i<count; i++){crc = charcrc8(str[i] ^ crc, reflect); }return crc ^ xorcrc;
}
简单的调用例子:
int main(int argc, char** argv)
{const char* str="123";if (argc >= 2) str = argv[1];for (int i=0; i<256; i++){printf("(%d->0x%02x-0x%02x) ", i, charcrc8(i), charcrc8(i, true));}printf("\n\n");printf("<%s> crc8 is 0x%02x, with reflect 0x%02x\n", str, calccrc8(str, strlen(str)), calccrc8(str, strlen(str), 0, true));return 0;
}
再附一些参考地址:
crc在线计算:https://crccalc.com/
crc计算方法:http://www.sunshine2k.de/articles/coding/crc/understanding_crc.html
reflect-table如何构建出来:https://stackoverflow.com/questions/28656471/how-to-configure-calculation-of-crc-table
crc在线计算:http://www.sunshine2k.de/coding/javascript/crc/crc_js.html
个人随笔 (Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu)
相关文章:

解读CRC校验计算
个人随笔 (Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu) 参考:http://www.sunshine2k.de/articles/coding/crc/understanding_crc.html 参考:https://en.wikipedia.org/wiki/Cyclic_redundancy_check 参考:https://www.cnblogs.com/…...
深入理解Spring MVC下
上一篇博客从理论概念上来梳理Spring MVC相关知识,此篇博客将通过spring官网提供showcase代码为例子,详细介绍showcase代码中包含的各个例子是如何实现的。官网的showcase代码包含的主要例子包括,Demo地址:Mapping Requests&#…...

【Linux】ssh-keygen不需要回车,自动生成密钥,批量免密操作!
使用命令ssh-keygen 需要手动敲击回车,才会生成密钥,如下代码所示 [rootlocalhost ~]# ssh-keygen Generating public/private rsa key pair. Enter file in which to save the key (/root/.ssh/id_rsa): Enter passphrase (empty for no passphrase):…...

C/C++开发,无可避免的内存管理(篇四)-智能指针备选
一、智能指针 采用C/C开发堆内存管理无论是底层开发还是上层应用,无论是开发新手,还是多年的老手,都会不自觉中招,尤其是那些不是自己一手经历的代码,要追溯问题出在哪里更是个麻烦事。C/C程序常常会遇到程序突然退出&…...
VMware ESXi给虚拟机扩容
用ESXi管理的虚拟机硬盘空间不够了,讲一下如何进行扩容。 一、查看现状 通过如下三个命令,可以查看硬盘情况,可以看到只有500G,已经用了45%。这次我们再扩容500G。 df -Th lsblk fdisk -lIDE磁盘的文件名为 /de…...
认识STM32和如何构建STM32工程
STM32介绍什么是单片机单片机(Single-Chip Microcomputer)是一种集成电路芯片,把具有数据处理能力的中央处理器CPU、随机存储器RAM、只读存储器ROM、多种/0口和中断系统、定时器/计数器等功能(可能还包括显示驱动电路、脉宽调制电路、模拟多路转换器、A/D转换器等电…...

RabbitMQ延迟队列
目录 一、概念 二、使用场景 三、RabbitMQ 中的 TTL (一)队列设置 TTL (二)消息设置 TTL (三)两者的区别 四、整合SpringBoot实现延迟队列 (一)创建项目 (二&am…...
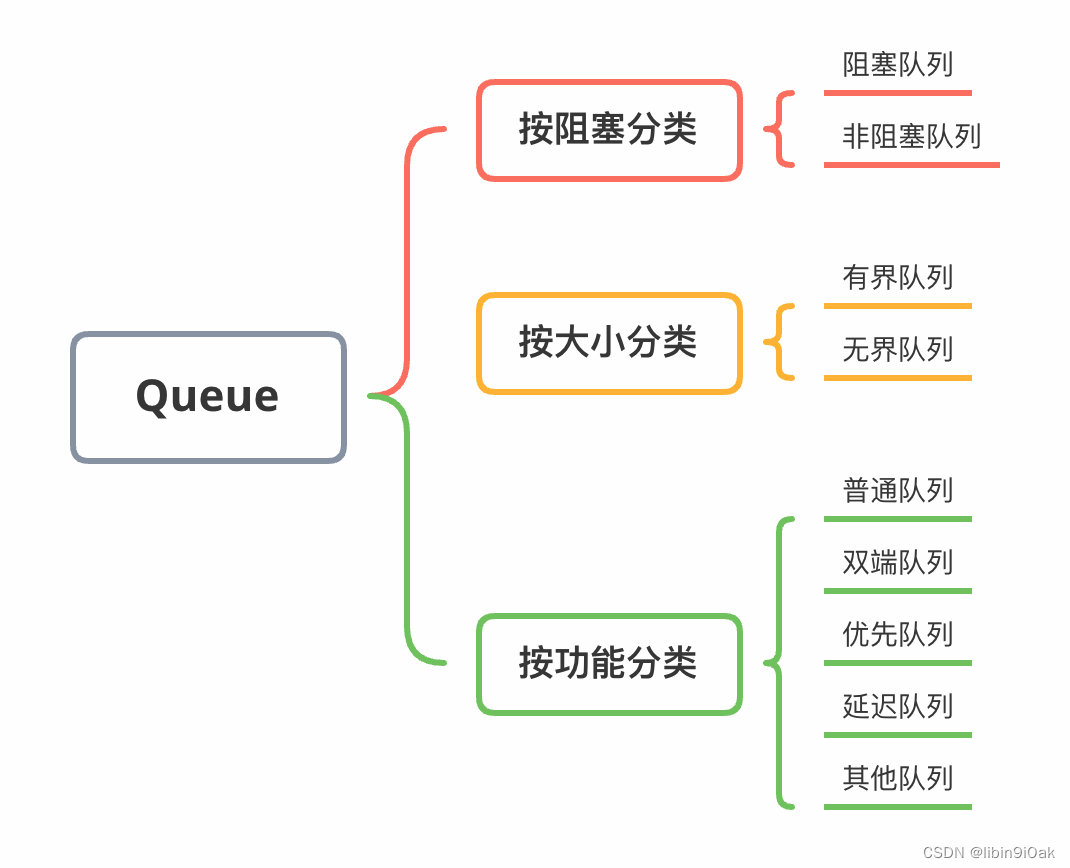
Java中常用的七种队列你了解多少?
文章目录Java中常用的七种队列你了解多少?ArrayBlockingQueue队列如何使用?添加元素到队列获取队列中的元素遍历队列LinkedBlockingQueue队列如何使用?1. 创建SynchronousQueue对象2. 添加元素到队列3. 获取队列中的元素4. 遍历队列SynchronousQueue队列…...
)
<Java获取时间日期工具类>常见八种场景(一)
一:自定义时间日期工具类常用的八种方式(整理): 0,getTimeSecondNum:时间日期转成秒数,常用于大小比较 1,getLastYearMonthLastDay:获取去年当月最后一天的时间日期 2,getLastYearM…...

接上一篇 对多个模型环形旋转进行优化 指定旋转位置
using System.Collections; using System.Collections.Generic; using UnityEngine; using DG.Tweening; public class ModelAnimal : MonoBehaviour { //记录鼠标滑动 public Vector2 lastPos;//鼠标上次位置 Vector2 currPos;//鼠标当前位置 Vector2 offset;//两次位置的偏移…...
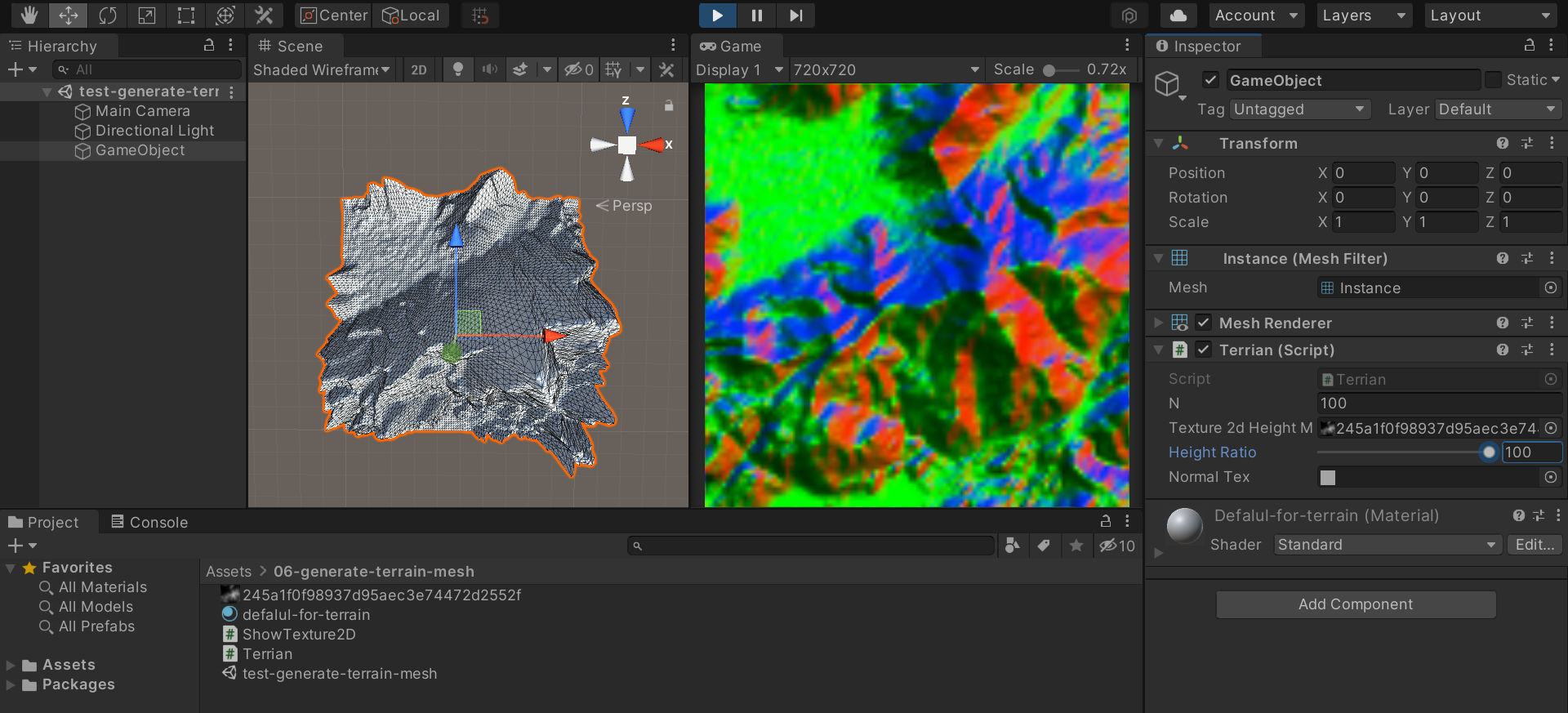
Unity中获取地形的法线
序之前,生成了地形图:(42条消息) 从灰度图到地形图_averagePerson的博客-CSDN博客那末,地形的法线贴图怎么获取?大概分为两个部分吧,先拿到法线数据,再画到纹理中去。关于法线计算Unity - Scripting API: M…...
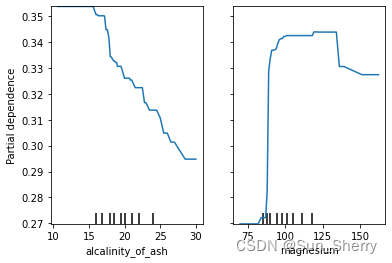
模型解释性:PFI、PDP、ICE等包的用法
本篇主要介绍几种其他较常用的模型解释性方法。 1. Permutation Feature Importance(PFI) 1.1 算法原理 置换特征重要性(Permutation Feature Importance)的概念很简单,其衡量特征重要性的方法如下:计算特征改变后模型预测误差的增加。如果打乱该特征的…...
)
spring常见面试题(2023最新)
目录前言1.spring是什么2.spring的设计核心是什么3.IOC和AOP面试题4.spring的优点和缺点5.spring中bean的作用域6.spring中bean的注入方式7.BeanFactory 和 ApplicationContext有什么区别?8.循环依赖的情况,怎么解决?9.spring中单例Bean是线程…...

华为OD机试题,用 Java 解【压缩报文还原】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...
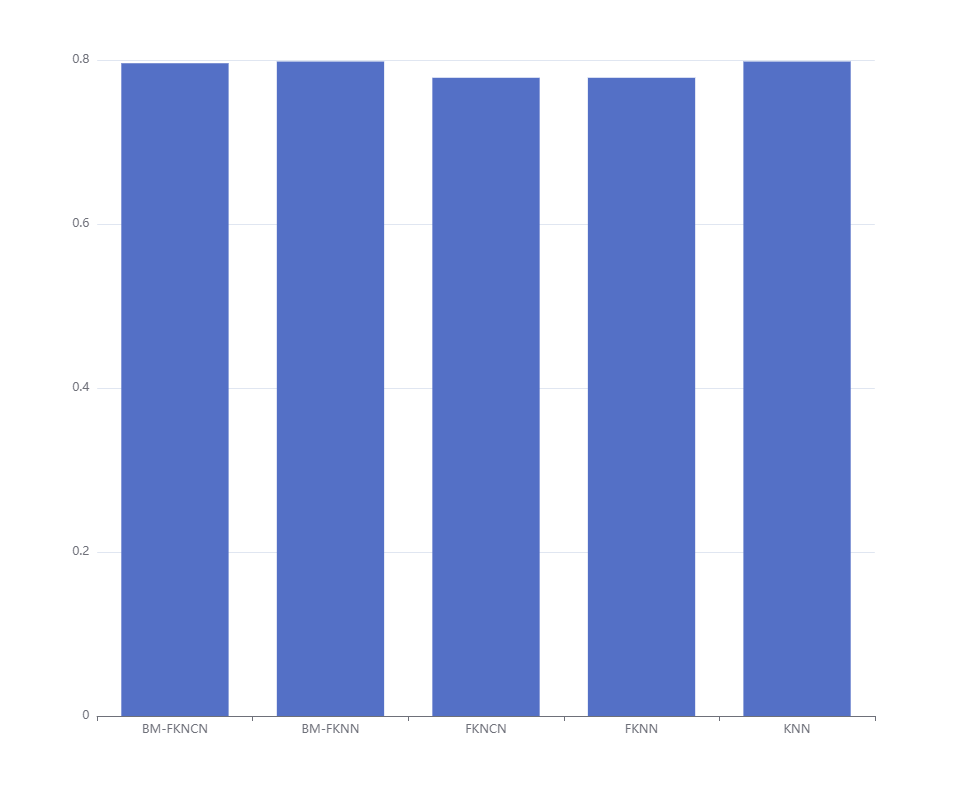
机器学习-BM-FKNCN、BM-FKNN等分类器对比实验
目录 一、简介和环境准备 二、算法简介 2.1四种方法类: 2.1.1FKNN 2.1.2FKNCN 2.1.3BM-FKNN 2.1.3BM-FKNCN 2.2数据预处理 2.3输出视图 2.4调用各种方法看准确率 2.4.1BM-FKNCN 2.4.2BM-FKNN 2.4.3FKNCN 2.4.4FKNN 2.4.5KNN 一、简介和环境准备 k…...

ChatGPT火了,对话式人工智能还能干嘛?
身兼数职的ChatGPT 从2022火到了2023 连日来一直是各大平台的热议对象 其实除了写诗、敲代码、处理文档 以ChatGPT为代表的 对话式人工智能 还有更重要的工作要做 对话式AI与聊天机器人 相信大多数人…...
)
十一、操作数栈的特点(Operand Sstack)
1.每一个独立的栈帧中除了包含局部变量表以外,还包含一个后进先出的操作数栈,也可以称之为表达式栈。 2.操作数栈,在方法执行过程中,根据字节码指令,往栈中写入数据,或提取数据,即入栈ÿ…...

拆解瑞幸新用户激活流程,如何让用户“动”起来?
Aha时刻 一个产品的拉新环节,是多种方式并存的;新用户可能来自于商务搭建了新的渠道,运营策划了新的活动,企划发布了新的广告,销售谈下了新的客户,市场推广了新的群体,以及产品本身的口碑传播,功能更新带来的自然流量。 这是一个群策群力的环节,不同的团队背负不同的K…...
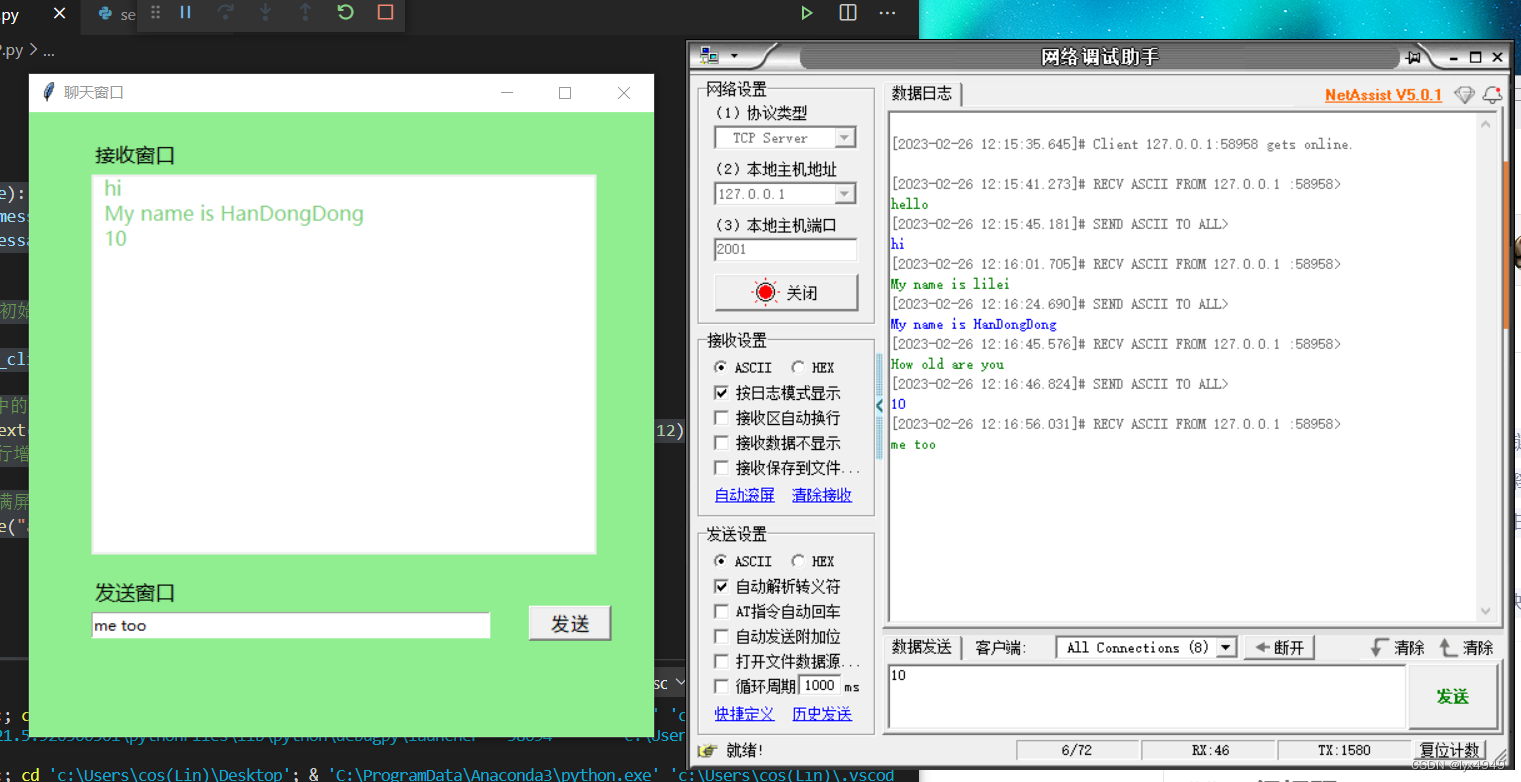
tkinter界面的TCP通信/开启线程等待接收数据
前言 用简洁的语言写一个可以与TCP客户端实时通信的界面。之前做了一个项目是要与PLC进行信息交互的界面,在测试的时候就利用TCP客户端来实验,文末会附上TCP客户端。本文分为三部分,第一部分是在界面向TCP发送数据,第二部分是接收…...

华为OD机试题,用 Java 解【任务混部】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
