【献给过去的自己】栈实现计算器(C语言)
背景
记得在刚学C语言时,写了一篇栈实现计算器-CSDN博客文章。偶然间看到了文章的阅读量以及评论,居然有1.7w的展现和多条博友的点评,反馈。
现在回过头来看,的确有许多不严谨的地方,毕竟当时分享文章时,还未毕业。理论和思维还不够严谨。但是我还依稀记得,班级上当时写出这个程序的同学,稀疏可数。所以在当时,还是有骄傲的资本的。本着对技术精益求精的态度,再通过本篇文章希望能够帮助刚接触C语言的朋友,也是给过去的自己一个满意的答复~
规则
对于一个表达式,我们应该如何去识别它呢?当时,老师和我们说,按照如下规则进行解析即可。

当时我们并不懂这个规则的由来,只知道按照这个规则去编程即可。再后来的工作中,因为考《软件设计师》资格证,了解到上述的规则,其实就是后缀表达式。同理还有前缀表达式,中缀表达式。
中缀表达式
中缀表达式就是我们常用的一种算数表示方式。它的特点是操作符以中缀的方式处于操作数中间。但是中缀表达比较适合人类计算,对于计算机而言过于复杂。前缀表达式和后缀表达式对于计算机而言,更加友好。
因此,我们想用程序实现计算器功能,有两种方式:
中缀表达式--> 前缀表达式-->计算
中缀表达式--> 后缀表达式-->计算
前缀表达式
前缀表达式的运算符位于两个操作数之前,又称为前缀记法或波兰式。比如表达式(中缀)5+4,前缀表达式+ 5 4。因此使用前缀表达式进行计算,需要两个步骤。
-
如何将中缀表达式转换为前缀表达式
-
计算机如何识别前缀表达式并计算
中缀表达式转换前缀表达式
根据文中描述,中缀表达式转换为前缀表达式的规则如下:
-
初始化两个栈:运算符栈S1和存储中间结果的栈S2;
-
从右至左扫描中缀表达式;
-
遇到操作数时,将其压入S2;
-
遇到运算符时,比较其与S1栈顶运算符的优先级;
-
如果S1为空,或栈顶运算符为右括号
),则将此运算符入栈; -
否则,若优先级比栈顶运算符的较高或相等,也将运算符压入S1;
-
否则,将S1栈顶的运算符弹出并压入到S2,再次转到
4.1与S1中新的栈顶运算符相比较;
-
-
遇到括号时:
-
如果是右括号
),则直接压入S1; -
如果是左括号
(,则依次弹出S1栈顶的运算符,并压入S2,直到遇到右括号为止,此时将这一对括号丢弃;
-
-
重复步骤
2至5,直到表达式的最左边; -
将S1中剩余的运算符依次弹出并压入S2;
-
依次弹出S2中的元素并输出,结果即为中缀表达式对应的前缀表达式。
虽然规则很复杂,但是编码难度并不是很大,大家可以按照自己的技术能力尝试一下。
分析思路
我们以表达式1+(2+3)*4-5举例。
1. 因为输入表达式是字符串,后续我们需要从右往左扫描表达式,因此首先需要将字符串表达式中的运算符和操作数进行区分,可以用整型数组如下图:

2. 根据2至5规则,进行分析。


3. 弹出S2中的数据元素:- + 1 * + 2 3 4 5;
代码示例
我的代码示例如下:
#include<stdlib.h>
#include<stdio.h>
#include<string.h>
#include<stdint.h>
#include<stdbool.h>#define STACK_LEN 1024/** 中缀表达式栈*/
static int32_t g_infix_expression[1024] = {0};/** 前缀表达式栈*/
static int32_t g_prefix_expression[1024] = {0};/** 后缀表达式栈*/
static int32_t g_suffix_expression[1024] = {0};/*** @brief 将输入的字符串表达式转换为中缀表达式** @param [in] expression 字符串表达式* @return int 0 成功 non-0 失败* */
int expression2infix(const char* expression)
{if(expression == NULL){printf("input error\n");return -1;}int dataTmp = 0; //表达式中的操作数bool dataFlag = false; // 操作数标识,表示当前是否有数据需要入栈const char* ptr = expression;int32_t* infix_index = g_infix_expression;printf("expression = %s\n",expression);while(*ptr != '\0'){/** 字符为数字*/if('0' <= *ptr && *ptr <= '9'){dataTmp = dataTmp*10 +(*ptr - '0');dataFlag = true;}/**字符为操作符或括号*/else if(*ptr == '+' || *ptr == '-' || *ptr == '*' || *ptr == '/' || *ptr == '(' || *ptr == ')'){if(dataFlag == true){*(infix_index++) = dataTmp;dataFlag = false;dataTmp = 0;}*(infix_index++) = *ptr;}else{printf("wrong exptrssion\n");return -1;}ptr++;}/**将最后一个操作数,入栈*/if(dataFlag == true){*(infix_index++) = dataTmp;dataFlag = false;dataTmp = 0;}return 0;
}/*** @brief 将中缀表达式转换为前缀表达式** @return int 0 成功 non-0 失败* */
int infix2prefixExpression()
{/**初始化运算符栈和中间结果栈*/int32_t stack_s1[STACK_LEN] = {0};int32_t stack_s1_top = 0;int32_t stack_s2[STACK_LEN] = {0};int32_t stack_s2_top = 0; int32_t * index = g_infix_expression;/**获取中缀表达式最右侧操作数*/while(*(index+1) != 0){index++;}while(index != g_infix_expression){/** 操作符*/if(*index == '+' || *index == '-' || *index == '*' || *index == '/'){while(true){/**S1为空,或栈顶运算符为右括号),则将此运算符入栈*/if(stack_s1_top == 0 || stack_s1[stack_s1_top-1] == ')' || stack_s1[stack_s1_top-1] == '-'|| stack_s1[stack_s1_top-1] == '+'){stack_s1[stack_s1_top++] = *index;break;}stack_s2[stack_s2_top++] = stack_s1[stack_s1_top-1];stack_s1[stack_s1_top-1] = 0;stack_s1_top = stack_s1_top -1;}}/**左括号* 则依次弹出S1栈顶的运算符,并压入S2,直到遇到右括号为止*/else if(*index == '('){while(true){/**异常*/if(stack_s1_top == 0){printf("infix experssion worong\n");return -1;}/**遇到右括号,丢弃括号*/if(stack_s1[stack_s1_top-1] == ')'){stack_s1[stack_s1_top-1] = 0;stack_s1_top = stack_s1_top -1;break;}/**其它符号需要入栈S2*/else{stack_s2[stack_s2_top++] = stack_s1[stack_s1_top-1];stack_s1[stack_s1_top-1] = 0;stack_s1_top--;}}}/**右括号* 直接入运算符栈s1*/else if(*index == ')'){stack_s1[stack_s1_top++] = *index;}/** 操作数* 直接加入栈s2*/else{stack_s2[stack_s2_top++] = *index;}index--;
#if 0printf("==============\n");printf("stack_s1=");for(int i = 0 ; i < stack_s1_top; i++){(stack_s1[i] > 9) ? (printf("%c ",stack_s1[i])):(printf("%d ",stack_s1[i]));}printf("\n");printf("stack_s2=");for(int i = 0 ; i < stack_s2_top; i++){(stack_s2[i] > 9) ? (printf("%c ",stack_s2[i])):(printf("%d ",stack_s2[i]));}printf("\n");
#endif }/**将最左侧操作数压入s2*/stack_s2[stack_s2_top++] = *index;/**将s1中的符号压入s2*/for(int i = stack_s1_top - 1; i >= 0; i-- ){stack_s2[stack_s2_top++] = stack_s1[i];stack_s1[i] = 0; }/**将s2中的数据弹出,放入前缀表达式栈中*/for(int i = 0 ; stack_s2_top > 0; i++,stack_s2_top--){g_prefix_expression[i] = stack_s2[stack_s2_top-1];}return 0;
}int main(int argc,char* argv[])
{if(argc != 2){printf("please input experssion\n");return -1;}int32_t iRet = 0;iRet = expression2infix(argv[1]);if(iRet == 0){for(int i = 0 ; i < STACK_LEN && g_infix_expression[i] != 0; i++){if(g_infix_expression[i] == '+' || g_infix_expression[i] == '-' || g_infix_expression[i] == '*' || g_infix_expression[i] == '/'){printf("%c ",g_infix_expression[i]);}else{printf("%d ",g_infix_expression[i]);}}printf("\n");}iRet = infix2prefixExpression();if(iRet == 0){for(int i = 0 ; i < STACK_LEN && g_prefix_expression[i] != 0; i++){if(g_infix_expression[i] == '+' || g_infix_expression[i] == '-' || g_infix_expression[i] == '*' || g_infix_expression[i] == '/'){printf("%c ",g_infix_expression[i]);}else{printf("%d ",g_infix_expression[i]);}}printf("\n");}prefixExpressionCaculate();return 0;
}
前缀表达式计算
前缀表达式的计算规则如下:
-
从右至左扫描表达式;
-
遇到数字,压入栈中;
-
遇到运算符,弹出栈顶的两个数,并用运算符对这两个数做相应的计算,并将结果入栈;
-
重复上述
2,3步骤,直到表达式最左端,最后的值为表达式的结果。
分析思路
以上述后缀表达式举例:- + 1 * + 2 3 4 5。

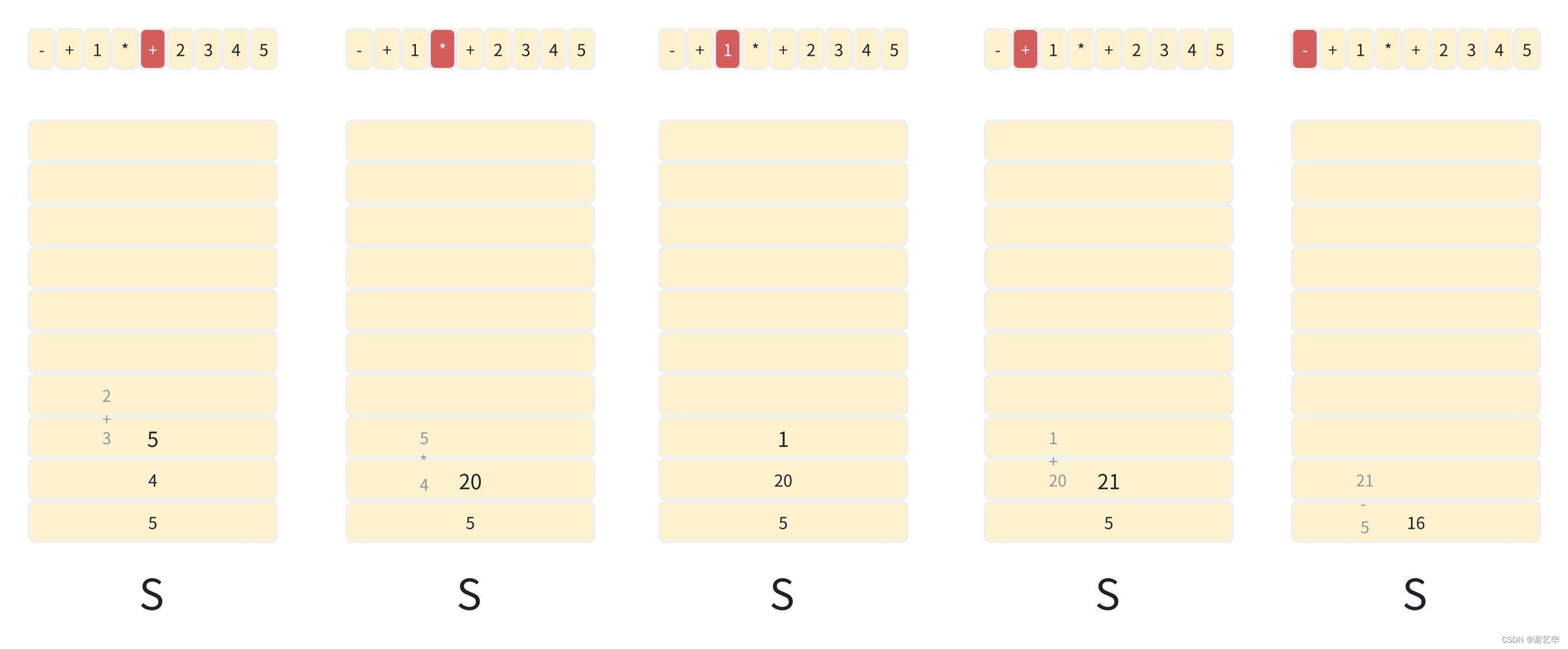
得出结果为16。
代码示例
新增prefixExpressionCaculate接口。代码如下:
/*** @brief 将前缀表达式进行计算** @return int 0 成功 non-0 失败* */
int prefixExpressionCaculate()
{/**结果栈*/int32_t stack[1024] = {0};int32_t stack_len = 0;/**临时结果*/int32_t tmpResult = 0;int32_t data1 = 0;int32_t data2 = 0;/**获取后缀表达式的最右侧操作数*/int32_t* index = g_prefix_expression;while(*(index+1) != 0){index++;}while(index >= g_prefix_expression){/**弹出栈顶的两个数,并用运算符对这两个数做相应的计算,并将结果入栈*/if(*index == '+' || *index == '-' || *index == '*' || *index == '/'){data1 = stack[stack_len-1];data2 = stack[stack_len-2];if(*index == '+'){tmpResult = data1 + data2;}else if(*index == '-'){tmpResult = data1 - data2;}else if(*index == '*'){tmpResult = data1 * data2;}else if(*index == '/'){tmpResult = data1 / data2;}else{printf("worng prefixExperssion\n");return -1;}stack[stack_len-1] = 0;stack[stack_len-2] = tmpResult;stack_len --;}/**遇到数字,压栈*/else{stack[stack_len] = *index;stack_len ++;}index --;}printf("result = %d\n",stack[0]);return 0;
}演示

后缀表达式
后缀表达式与前缀表达式类似,只是运算符位于两个相应操作数之后,后缀表达式也称为后缀记法或逆波兰式。同样,我们需要解决两个问题。
-
如何将中缀表达式转换为后缀表达式
-
后缀表达式的计算规则
中缀表达式转后缀表达式
根据文中描述,中缀表达式转换为后缀表达式的规则如下:
-
初始化两个栈:运算符栈S1和存储中间结果的栈S2;
-
从左至右扫描中缀表达式;
-
遇到操作数时,将其压入S2;
-
遇到运算符时,比较其与S1栈顶运算符的优先级;
-
如果S1为空,或栈顶运算符为左括号
(,则将此运算符入栈; -
否则,若优先级比栈顶运算符的高,也将运算符压入S1;(注意是必须为高,相同或低于都不行)
-
否则,将S1栈顶的运算符弹出并压入到S2,再次转到
4.2与S1中新的栈顶运算符相比较;
-
-
遇到括号时:
-
如果是左括号
(,则直接压入S1; -
如果是右括号
),则依次弹出S1栈顶的运算符,并压入S2,直到遇到左括号为止,此时将这一对括号丢弃;
-
-
重复步骤
2至5,直到表达式的最右边; -
将S1中剩余的运算符依次弹出并压入S2;
-
依次弹出S2中的元素并输出,结果即为中缀表达式对应的后缀表达式。
后缀表达式计算规则
后缀表达式的计算规则如下:
-
从左至右扫描表达式;
-
遇到数字,压入栈中;
-
遇到运算符,弹出栈顶的两个数,并用运算符对这两个数做相应的计算,并将结果入栈;
-
重复上述
2,3步骤,直到表达式最右端,最后的值为表达式的结果。
后缀表达式的代码示例可以参考前缀表达式的分析思路和代码,大家可以尝试编写。
总结
时间流逝,在竞争激烈的社会背景下,我们的身处IT行业,不断逼迫自己去学习,去成长。但是总会觉得自己做的还不够。为什么总是赶不上别人的脚步,陷入怀疑自我的处境。
朋友们,偶尔回头看看来时路上的自己,你会发现,你一直在成长,你的努力一直是正向反馈着你,不要轻视自己的努力。感谢csdn给予记录成长的平台,也感谢一直努力的自己。共勉~
参考文档
前缀表达式、中缀表达式和后缀表达式 - 乘月归 - 博客园
数据结构和算法(六):前缀、中缀、后缀表达式
相关文章:

【献给过去的自己】栈实现计算器(C语言)
背景 记得在刚学C语言时,写了一篇栈实现计算器-CSDN博客文章。偶然间看到了文章的阅读量以及评论,居然有1.7w的展现和多条博友的点评,反馈。 现在回过头来看,的确有许多不严谨的地方,毕竟当时分享文章时,还…...

如何利用ChatGPT撰写学术论文?
在阅读全文前请注意,本文是利用ChatGPT“辅助完成”而不是“帮写”学术论文,请一定要注意学术规范! 本文我将介绍如何使用清晰准确的“指令”让ChatGPT帮助我们在论文写作上提高效率,希望通过本文的指导,读者能够充分…...

【PG】PostgreSQL高可用方案repmgr管理之配置文件
1 配置文件 1.1 配置文件格式 repmgr.conf是一个纯文本文件,每行包含一个参数/值组合。 空格是无关紧要的(除了在带引号的参数值内),并且空行将被忽略。#将该行的其余部分指定为注释。不是简单标识符或数字的参数值应该用单引号…...

labelme自动标注工具
可以实现多图中相同目标的追踪,自动标注目标位置,速度极快,有需要评论...

【C++学习手札】模拟实现vector
🎬慕斯主页:修仙—别有洞天 ♈️今日夜电波:くちなしの言葉—みゆな 0:37━━━━━━️💟──────── 5:28 🔄 ◀️ ⏸ ▶️ ☰…...

Python将图片按照表格形式排列
图片按照表格的形式排列,可以使用图像处理库Pillow来实现 事例代码 from PIL import Image, ImageDraw# 创建一个画布,用来存放排列后的图片 canvas Image.new(RGB, (800, 600), white)# 读取图片 im1 Image.open(image1.jpg) im2 Image.open(image…...

Linux 简要命令记录
1、设置时区: #设为上海: timedatectl set-timezone Asia/Shanghai #搜索特定时区 timedatectl list-timezone2、修改时间: #设定系统时间 date -s "2023-11-16 22:30:00" #同步写入BIOS hwclock -w3、fdisk分区 rootheihei:~# …...

深度学习与深度强化学习
1. 深度学习中卷积层的作用是什么?全连接层的作用是什么?二者有什么联系和区别? 在深度学习中,卷积层(Convolutional Layer)和全连接层(Fully Connected Layer)是神经网络中常见的两…...

C++函数重载中形参是引用类型和常量引用类型的调用方法
void fun(int &a) {cout<<"调用func(int &a)<<endl; }void fun(const int &a) {cout<<"调用func(const int &a)<<endl; }int main() {// 1.调用引用类型的函数int a10;func(a);// 2.调用常量引用类型的函数,因为…...
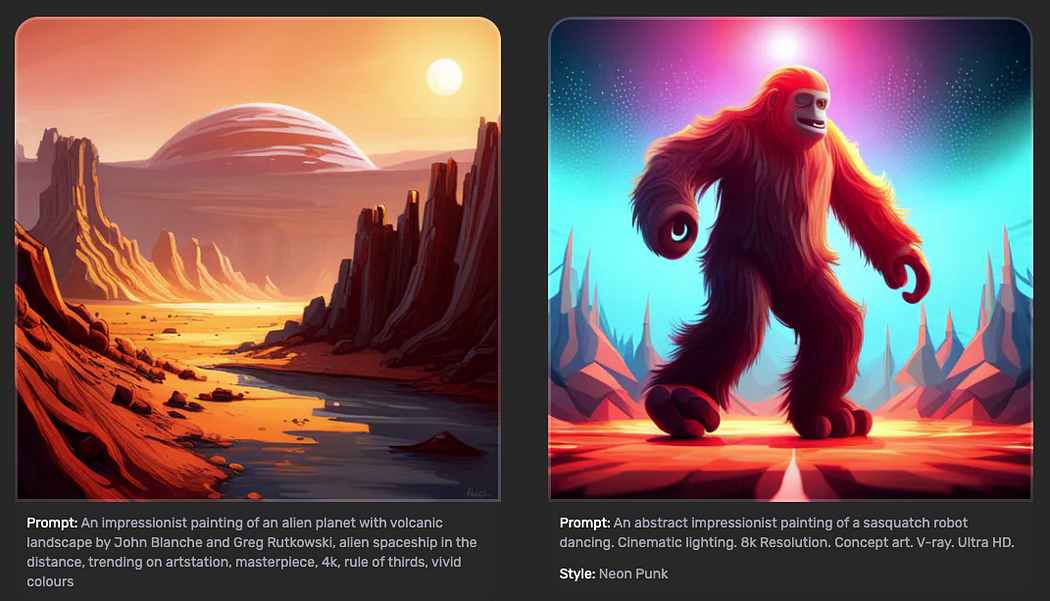
Quest 3期间Sui上游戏处理了数百万笔交易
Sui固有的可扩展性和低且可预测的gas费使其成为Web3游戏的理想平台。在Quest 3中,参与的游戏项目处理了数百万笔交易,这毫无疑问地展示了Sui卓越的能力。 Quest 3的主题是游戏,让开发者有机会向潜在玩家介绍他们激动人心的创作。鼓励这些玩家…...

Python中如何定义类、基类、函数和变量?
在Python中,定义类、基类、函数和变量是非常常见的操作。以下是简单的示例: 定义类: class Animal:def __init__(self, name):self.name namedef make_sound(self):passclass Dog(Animal):def make_sound(self):return "Woof!"上…...
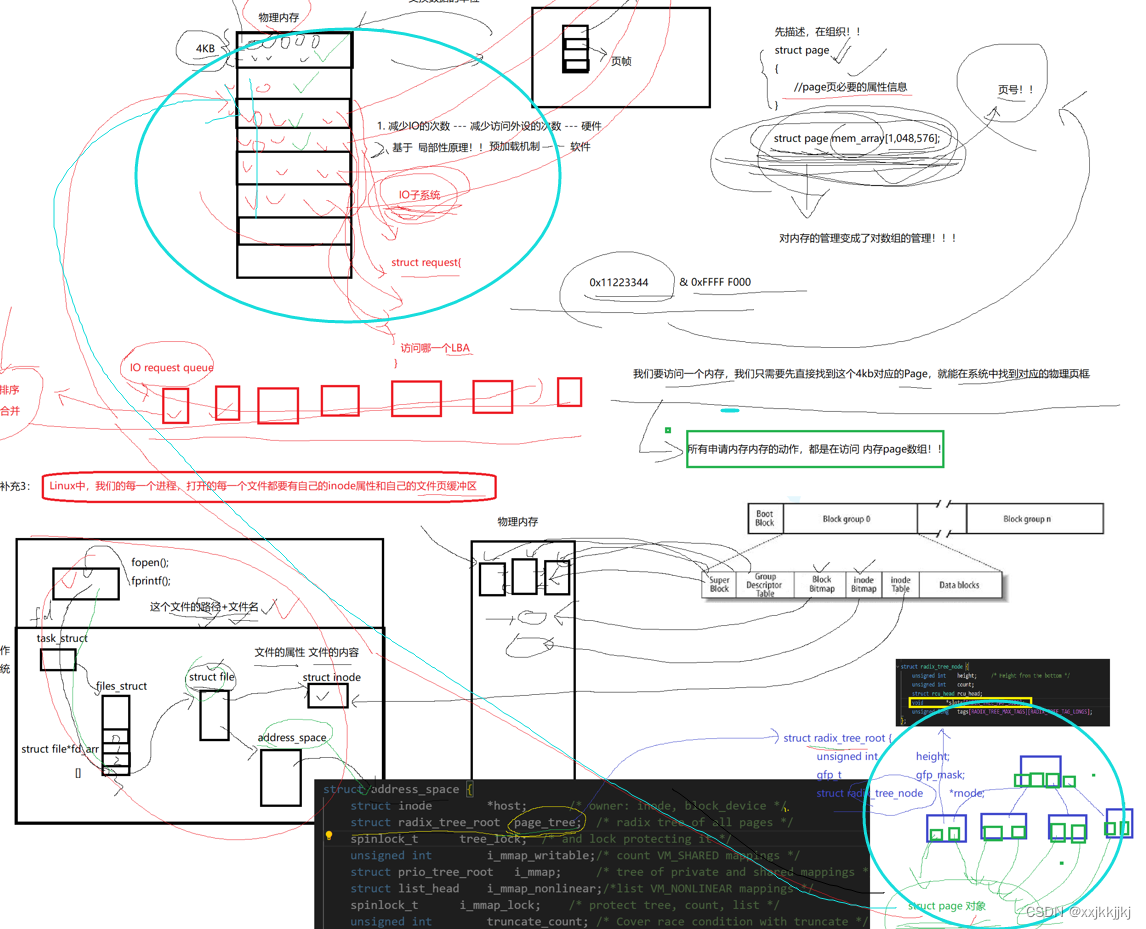
打开文件 和 文件系统的文件产生关联
补充1:硬件级别磁盘和内存之间数据交互的基本单位 OS的内存管理 内存的本质是对数据临时存/取,把内存看成很大的缓冲区 物理内存和磁盘交互的单位是4KB,磁盘中未被打开的文件数据块也是4KB,所以磁盘中页帧也是4KB,内存…...
【Rust】快速教程——模块mod与跨文件
前言 道尊:没有办法,你的法力已经消失,我的法力所剩无几,除非咱们重新修行,在这个世界里取得更多法力之后,或许有办法下降。——《拔魔》 \;\\\;\\\; 目录 前言跨文件mod多文件mod 跨文件mod //my_mod.rs…...
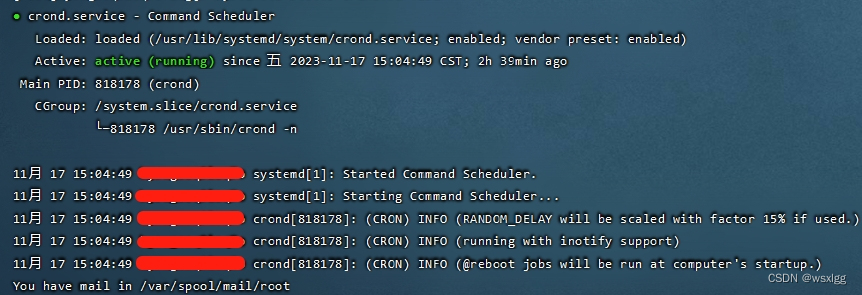
crontab定时任务是否执行
centos查看 crontab 是否启动 systemctl status crond.service 查看cron服务的启动状态 systemctl start crond.service 启动cron服务[命令没有提示] systemctl stop crond.service 停止cron服务[命令没有提示] systemctl restart crond.service 重启cron服务[命令没有提示] s…...

MATLAB程序设计:牛顿迭代法
function xnewton(x0,e,N,fx) %输入x0,误差限e,迭代次数N和函数Fx k1; while k<Nif subs(diff(fx),x0)0disp("输出奇异标志");break;endx1x0-subs(fx,x0)/subs(diff(fx),x0);if abs(x1-x0)<ebreak;endx0x1;kk1; end if k<Ndisp(x1); elsedisp("迭代失败…...

B031-网络编程 Socket Http TomCat
目录 计算机网络网络编程相关术语IP地址ip的概念InerAdress的了解与测试 端口URLTCP、UDP和7层架构TCPUDPTCP与UDP的区别和联系TCP的3次握手七层架构 Socket编程服务端代码客户端代码 http协议概念Http报文 Tomcat模拟 计算机网络 见文档 网络编程相关术语 见文档 IP地址 …...

gRPC之metadata
1、metadata 服务间使用 Http 相互调用时,经常会设置一些业务自定义 header 如时间戳、trace信息等,gRPC使用 HTTP/2 协议自然也是支持的,gRPC 通过 google.golang.org/grpc/metadata 包内的 MD 类型提供相关的功能接口。 1.1 类型定义 /…...
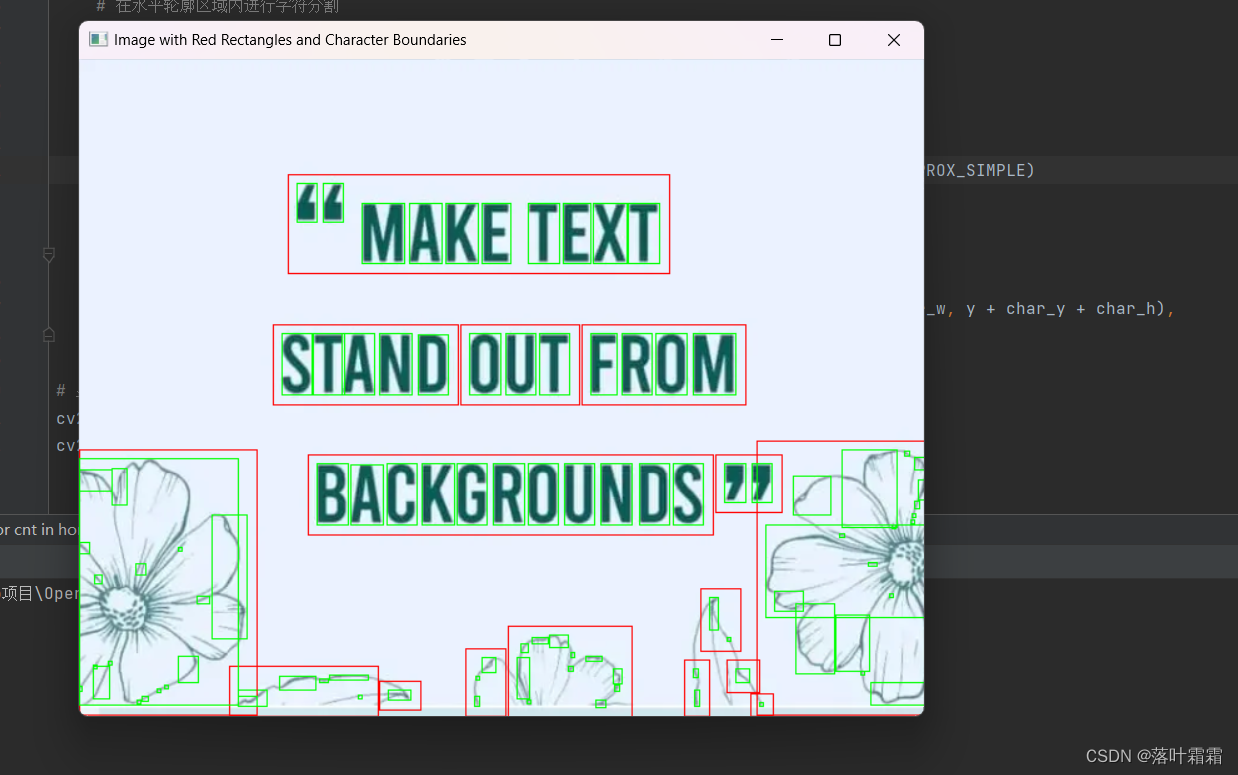
【OpenCV实现图像:OpenCV进行OCR字符分割】
文章目录 概要基本概念读入图像图像二值化小结 概要 在处理OCR(Optical Character Recognition,光学字符识别)时,利用传统的图像处理方法进行字符切分仍然是一种有效的途径。即便当前计算机视觉领域主导的是卷积神经网络…...

景联文科技入选量子位智库《中国AIGC数据标注产业全景报告》数据标注行业代表机构
量子位智库《中国AIGC数据标注产业全景报告》中指出,数据标注处于重新洗牌时期,更高质量、专业化的数据标注成为刚需。未来五年,国内AI基础数据服务将达到百亿规模,年复合增长率在27%左右。 基于数据基础设施建设、大模型/AI技术理…...
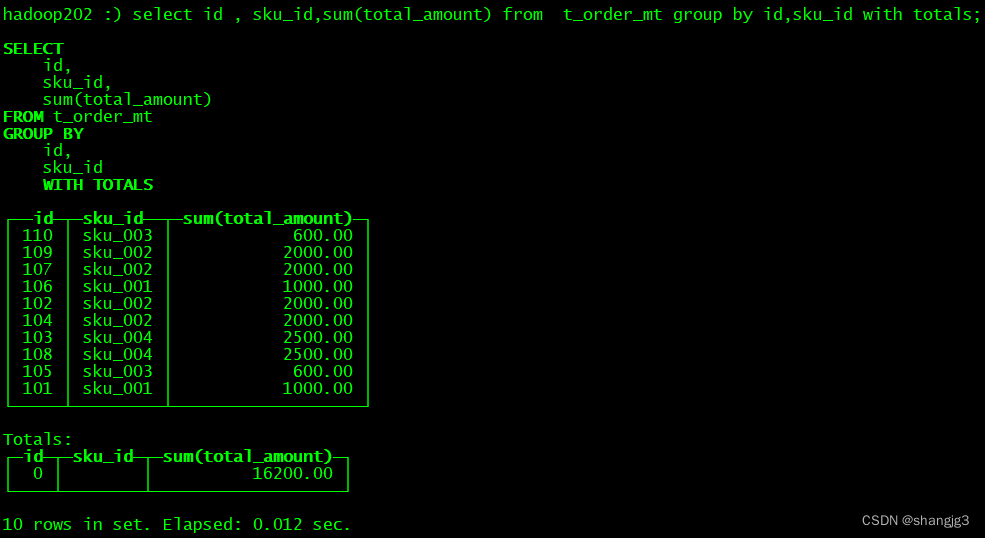
ClickHouse SQL操作
基本上来说传统关系型数据库(以MySQL为例)的SQL语句,ClickHouse基本都支持,这里不会从头讲解SQL语法只介绍ClickHouse与标准SQL(MySQL)不一致的地方。 1 Insert 基本与标准SQL(MySQL)…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...
