剑指offer --- 用两个栈实现队列的先进先出特性
目录
前言
一、读懂题目
二、思路分析
三、代码呈现
总结
前言
当我们需要实现队列的先进先出特性时,可以使用栈来模拟队列的行为。本文将介绍如何使用两个栈来实现队列,并给出具体的思路和代码实现。
一、读懂题目
题目:用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead,分别完成在队列尾部插入结点和在队列头部删除结点的功能。
当我们需要利用栈来实现队列先进先出的特性时,考虑到单个栈对存入的一组数据push后再逐位pop取出,对应的序列和输入的顺序相反,那我们是否可以用两个栈,抽象类似于负负得正的手法,使得top位逐个取出得到的序列和插入时是相同的?
二、思路分析
首先基础类定义如下,我们只需要补充里面 appendTail 和 deleteHead 两函数的定义即可:
// 用两个栈实现队列
template<typename T>
class MyQueue
{
public:void appendTail(const T& n);T deleteHead();
private:stack<T> st1;stack<T> st2;};为了便于表示和说明,设定一组数据 {a, b, c, d, e} 作为测试序列。
我们看到两个栈都可存储数据,那我们不妨先将数据全部存入st1中,那么根据栈先进后出的特性,两栈中数据的存储此时应该是这样的:
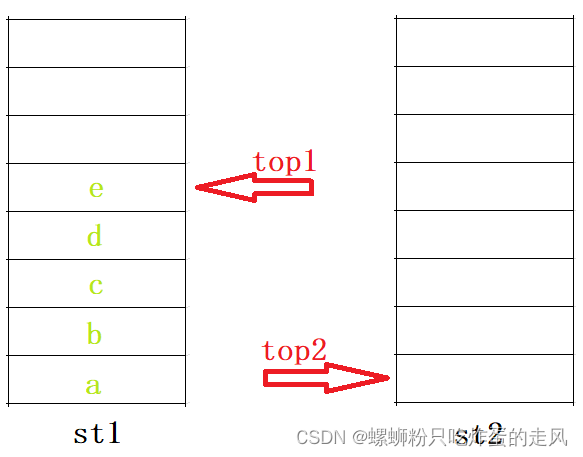
既然我们想到试试“负负得正”这种方法,那要是把st1中的元素再一 一取出放入st2中,是不是相当于把序列的顺序调转再调转,这样当我们不断取 st2.top() 时,最后按照取出的序列就是原来顺序的初始序列!
我们模拟一下这个过程:
1)对st1执行两次取首压入st2中:
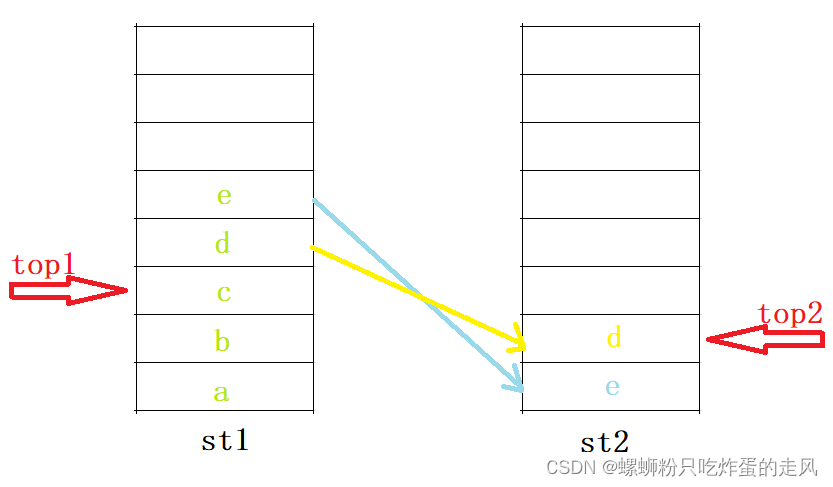
2)将剩余元素从st1中全部压入st2中,此时st1为空:
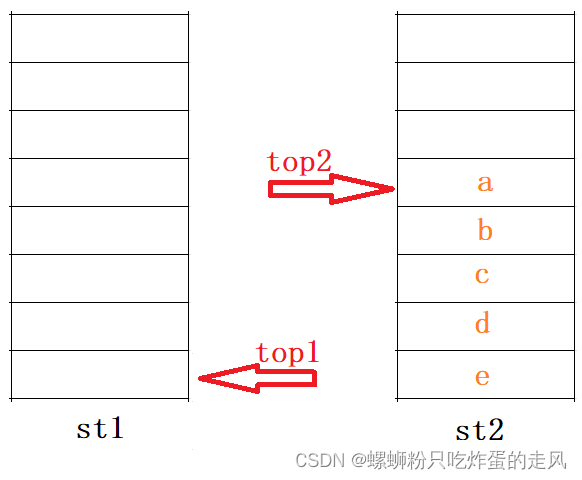
3)最后每当该模拟队列执行一次 front() 操作就返回 top2 所指向的值,每次 pop() 就从 st2 取出栈顶元素(前提是st1为空),直到 st2 栈为空:
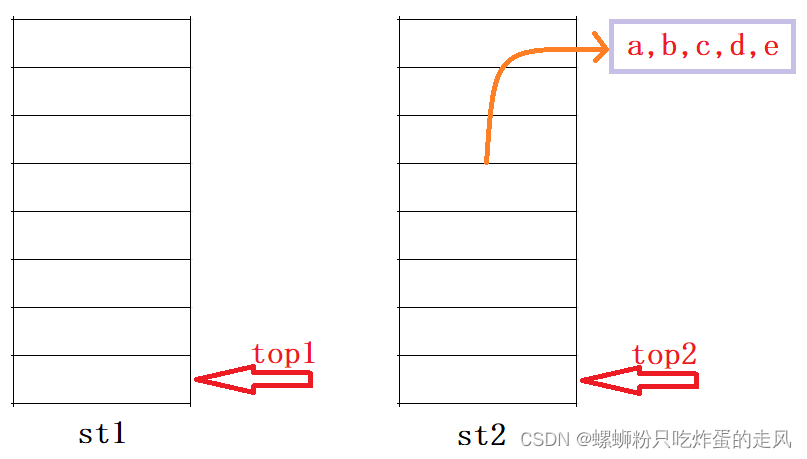
那如果在执行 front() 过程中,夹杂着新的push()指令,应该将新元素放入st1还是st2呢?如果st1不为空,要先将st1全部按照上面的规则移入st2后再插入还是先放入st1栈顶,再统一移入st2呢?
首先我们明确每个元素都需要经历“负负得正”的过程,所以首先新加元素肯定要先经过st1才能进入st2中。那是否需要st1及时清空呢?
我们不妨以 {a, b, c, d}, {e} 模拟两批次对模拟队列执行push()指令:
假定我们在每批操作结束就将该批的元素依次弹出并置入st2中,那么当需要输入上面第二组(即{e})时,st1和st2的存储情况如下:
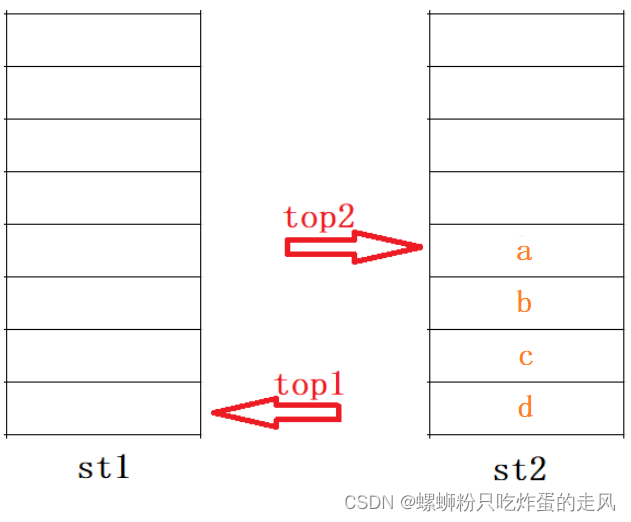
接下来该插入第二批数据了,但是实际功能调用过程中,不可能每次单批次插入操作之间是连续的,中间可能会有删除队列中已有元素的操作,所以我们不妨在两次 push() 指令中间加一句 pop_front() 指令,那么当接着执行一次pop_front() 指令时,对于st2而言应该将 a 元素剔除。同时我们注意到 a 元素正如我们所料位于st2的栈顶,当 st2.pop() 操作执行时,取出 a 元素,符合队列先进先出的特性。此时st1为空,st2顶部元素为b,如下图:
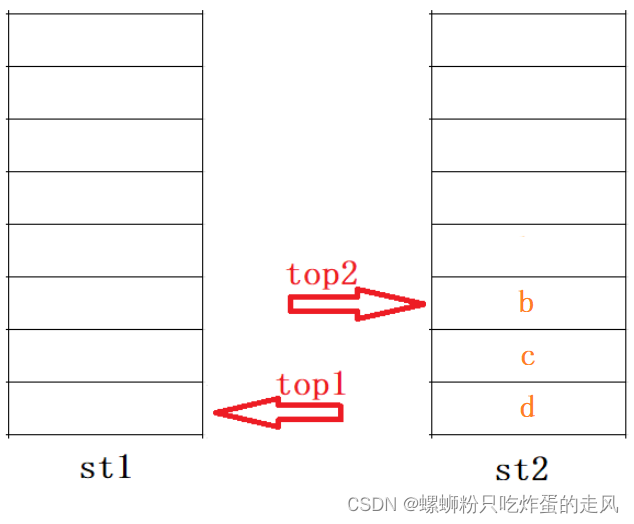
下一步我们进行第二批插入,将元素 e 执行 push() 操作时,显然 e 需要先进st1中,所以st1中此时不为空,元素e即为st1栈顶元素:
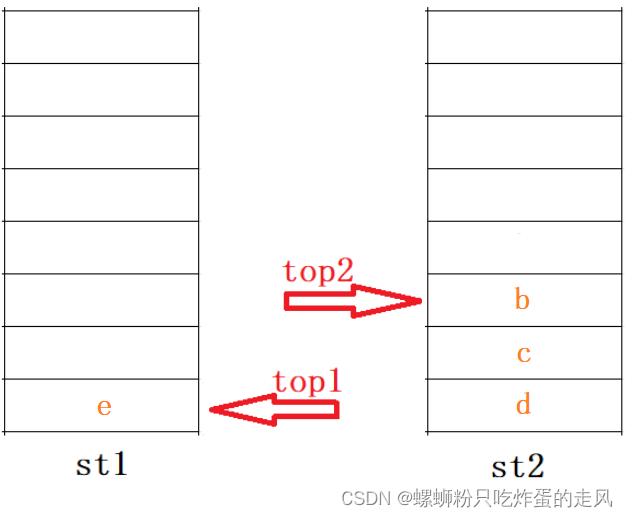
那么此时我们要不要把st1中的所有元素(这里仅有 e )顺手植入st2中呢?
1)如果移入st2中:
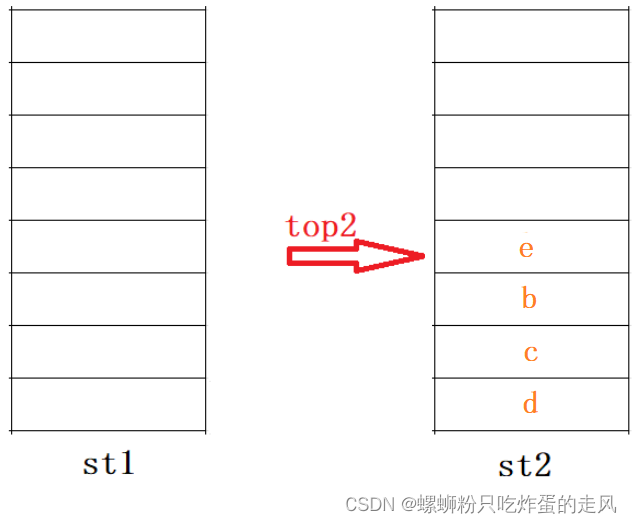
现在面临一个问题:如果我们一次性取出st2中的元素,亦或是仅取st2栈顶元素执行 st2.pop() 来获得理想的队列头,却发现得到的结果并不满足我们的设计需求,两轮输入的总序列为 {a, b, c, d, e} ,而取出序列为 {a, e, ... },显然不符合先进先出的原则。
那是否意味着第二批的输入元素应该先保存在st1中,并非单批输入结束后就将其接着压入st2中,那为什么首批输入的数据就可以直接经st1后全部置入st2呢?
难道因为开始时候 st2 为空吗?那如果后续其他批次插入时,也遵循 st2 为空后再将 st1 中所有元素置于 st2 中,会不会发生这样的冲突?
不妨我们按照这样的设计思路进行测试:
首先给出部分功能的此思路代码:
1)清空 st1 容器功能代码
template<typename T>
void MyQueue<T>::appendOver()
{if (st2.empty()) // 只有满足st2为空才清空st1{while (!st1.empty()){st2.push(st1.top());st1.pop();}}
}2)模拟 front() , push() 和 pop() 的函数功能
template<typename T>
T& MyQueue<T>::front()
{if (!st1.empty()){appendOver();}assert(!st2.empty());return st2.top();
}template<typename T>
void MyQueue<T>::appendTail(const T& n)
{st1.push(n);
}template<typename T>
T MyQueue<T>::deleteHead()
{assert(!empty()); // 不能同时为空if (st2.empty()){appendOver();}T tmp_poped = st2.top();st2.pop();return tmp_poped;
}3)实际测试代码
void test1()
{MyQueue<int> mq;// queue.push()模拟尾插for (int i = 10; i > 0; i--){mq.appendTail(i);} // 1 2 3 4 5 6 7 8 9 10 右侧栈顶// queue.front()模拟取首元素// appendTail()--push()模拟入队列操作// deleteHead()--pop()模拟删除队列首元素mq.deleteHead(); // st1中:空 st2中:1 2 3 4 5 6 7 8 9 右侧栈顶mq.appendTail(100); // st1中:100 st2中:1 2 3 4 5 6 7 8 9 右侧栈顶// 由于st2不为空,st1中元素不发生迁移// 经过上面两步 st1中:100 st2中:1 2 3 4 5 6 7 8 9// 假设我们再进行一组类似操作mq.deleteHead(); // st1中:100 st2中:1 2 3 4 5 6 7 8 右侧栈顶mq.appendTail(55); // st1中:55 100 st2中:1 2 3 4 5 6 7 8 右侧栈顶int val = mq.deleteHead(); // st1中:55 100 st2中:1 2 3 4 5 6 7 右侧栈顶printf("val = %d\n", val); // 8PopAndPrintMyQueue<int>(mq);
}按理来说结果应该和各行代码后面的理想推测相同,我们看看最后两行执行结果:
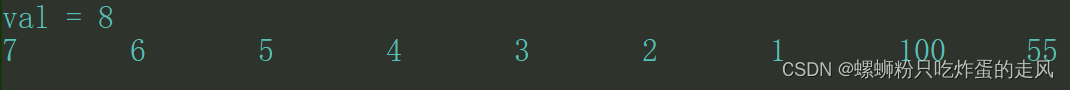 可以看到和我们推测的结果完全一致,我们不仅在上面完成了一组插入删除后,额外执行了一组插入和删除操作,最后打印整个模拟队列中剩余元素时,呈现的结果和传入的顺序也相同,同样可以采用其他各种操作,统计每次取出的元素组成的序列是否满足先进先出的特性,结果终究是符合的。
可以看到和我们推测的结果完全一致,我们不仅在上面完成了一组插入删除后,额外执行了一组插入和删除操作,最后打印整个模拟队列中剩余元素时,呈现的结果和传入的顺序也相同,同样可以采用其他各种操作,统计每次取出的元素组成的序列是否满足先进先出的特性,结果终究是符合的。
三、代码呈现
下面直接给出代码:
// 用两个栈实现队列
template<typename T>
class MyQueue
{
public:void appendTail(const T& n);T deleteHead();T& front();bool empty();
private:void appendOver(); // 将st1中元素的全部移入st2中 --- 前提:st2不为空stack<T> st1;stack<T> st2;};template<typename T>
void MyQueue<T>::appendTail(const T& n)
{st1.push(n);
}template<typename T>
void MyQueue<T>::appendOver()
{if (st2.empty()) // 只有满足st2为空才清空st1{while (!st1.empty()){st2.push(st1.top());st1.pop();}}
}template<typename T>
bool MyQueue<T>::empty()
{if (st1.empty() && st2.empty()){return true;}return false;
}template<typename T>
T MyQueue<T>::deleteHead()
{assert(!empty()); // 不能同时为空if (st2.empty()){appendOver();}T tmp_poped = st2.top();st2.pop();return tmp_poped;
}template<typename T>
T& MyQueue<T>::front()
{if (st2.empty()){appendOver();}assert(!st2.empty());return st2.top();
}template<typename T>
void PopAndPrintMyQueue(MyQueue<T>& my_q)
{while (!(my_q.empty())){cout << my_q.front() << "\t";my_q.deleteHead();}cout << endl;
}void test1()
{MyQueue<int> mq;// queue.push()模拟尾插for (int i = 10; i > 0; i--){mq.appendTail(i);} // 1 2 3 4 5 6 7 8 9 10 右侧栈顶// queue.front()模拟取首元素// appendTail()--push()模拟入队列操作// deleteHead()--pop()模拟删除队列首元素mq.deleteHead(); // st1中:空 st2中:1 2 3 4 5 6 7 8 9 右侧栈顶mq.appendTail(100); // st1中:100 st2中:1 2 3 4 5 6 7 8 9 右侧栈顶// 由于st2不为空,st1中元素不发生迁移// 经过上面两步 st1中:100 st2中:1 2 3 4 5 6 7 8 9// 假设我们再进行一组类似操作mq.deleteHead(); // st1中:100 st2中:1 2 3 4 5 6 7 8 右侧栈顶mq.appendTail(55); // st1中:55 100 st2中:1 2 3 4 5 6 7 8 右侧栈顶int val = mq.deleteHead(); // st1中:55 100 st2中:1 2 3 4 5 6 7 右侧栈顶printf("val = %d\n", val); // 8PopAndPrintMyQueue<int>(mq);
}
值得注意的是,上面对重要功能的安全性检查中,下面两种写法其本质是相同的:
// 1.
if (st2.empty())
{appendOver();
}
assert(!st2.empty());// 2.
assert(!empty()); // 不能同时为空
if (st2.empty())
{appendOver();
}总结
本文详细介绍了如何利用栈来实现队列的先进先出特性。通过使用两个栈,我们可以将插入的顺序和取出的顺序保持一致。文章讨论了具体的实现思路,并通过代码实例进行了测试。通过测试结果,我们验证了模拟队列的各种操作都满足先进先出的特性。这种使用栈实现队列的方法在实际应用中具有重要的意义。
相关文章:
剑指offer --- 用两个栈实现队列的先进先出特性
目录 前言 一、读懂题目 二、思路分析 三、代码呈现 总结 前言 当我们需要实现队列的先进先出特性时,可以使用栈来模拟队列的行为。本文将介绍如何使用两个栈来实现队列,并给出具体的思路和代码实现。 一、读懂题目 题目:用两个栈实现一…...
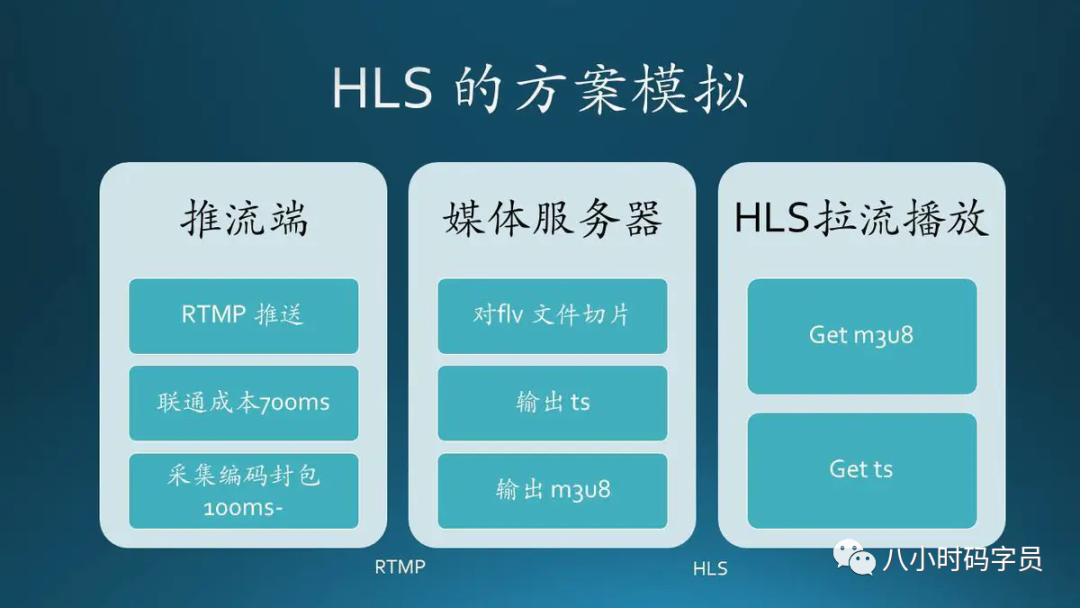
流媒体协议
◆ RTP(Real-time Transport Protocol),实时传输协议。 ◆ RTCP(Real-time Transport Control Protocol),实时传输控制协议。 ◆ RTSP(Real Time Streaming Protocol),实时流协议。 ◆ RTMP(Real Time Messaging Protocol),实时…...
ClickHouse的分片和副本
1.副本 副本的目的主要是保障数据的高可用性,即使一台ClickHouse节点宕机,那么也可以从其他服务器获得相同的数据。 Data Replication | ClickHouse Docs 1.1 副本写入流程 1.2 配置步骤 (1)启动zookeeper集群 (2&…...
)
C语言编程陷阱(五)
陷阱21:不要使用逗号运算符代替分号 C语言中,我们可以使用分号来结束一个语句,比如a = b;,这样可以让编译器知道语句的边界,以及执行的顺序。但是,如果我们想要在一个语句中执行多个表达式,就可以使用逗号运算符,比如a = (b = c, c + 1);,这样可以让编译器按照从左到右…...

chardet检测文件编码,使用生成器逐行读取文件
detect_encoding 函数使用 chardet 来检测文件的编码。然后,在 process_large_file 函数中,根据检测到的编码方式打开文件。这样,你就能够更准确地处理不同编码的文件。 import chardetdef detect_encoding(file_path):with open(file_path,…...

html所有标签和DOCTYPE的总结
一、DOCTYPE 1. 意义 DOCTYPE是一种标准通用标记语言的文档类型声明,告诉标准通用标记语言解析器它应该使用什么样的文档类型定义来解析文档。 2. 应用 现在,我们需要告诉标准通用标记语言解析器,我们接下去要用html来编写代码了。 <…...
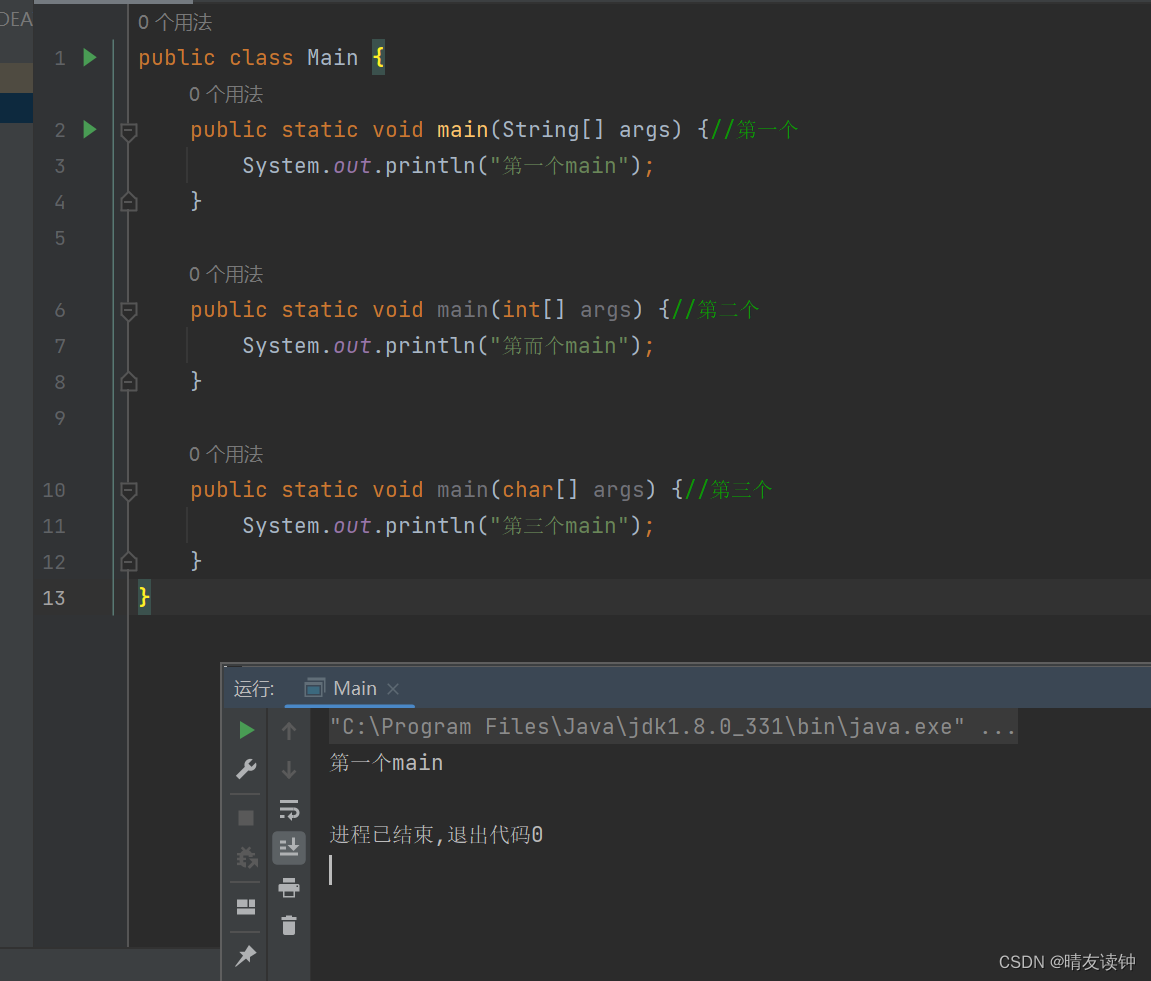
2023年11月15号期中测验判断题(Java)
1-1 局部变量可以与成员变量重名。 正确答案:T 解释: 局部变量可以和成员变量重名,通常,为了区分局部变量和成员变量,会使用this关键字(C称this指针,python是self关键字)来特别声…...
基于 selenium 实现网站图片采集
写在前面 有小伙伴选题,简单整理理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意,永不停息。所有其它的路都是不完整的,是人的逃避方式,是对…...

vue3相关内容
ref声明/赋值 操作基本类型数据 string number // 引入方法 import {ref} from vue // 声明变量 const name ref(A) // 修改值 name.value Breactive声明/赋值 操作引用类型数据 array object proxy不能直接赋值,会破坏响应式对象 // 引入方法 import {reacti…...

AWTK实现汽车仪表Cluster/DashBoard嵌入式GUI开发(七):FreeRTOS移植
前言: 一般的GUI工程都需要一个操作系统,可能是linux,重量级的,也可能是FreeRTOS,轻量级的。 一句话理解那就是工程就是FreeRTOS task任务的集合。 一个main函数可以看到大框架: 很显然,除了第一个是硬件配置的初始化,中间最重要的部分就是要创建任务,把AWTK的应用…...
《洛谷深入浅出进阶篇》P1995 程序自动分析——并查集,离散化
上链接:P1955 [NOI2015] 程序自动分析 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)https://www.luogu.com.cn/problem/P1955 上题干: 首先给你一个整数t,代表t次操作。 每一次操作包含以下内容: 1.给你一个整数n,让…...

基于单片机的自动循迹小车(论文+源码)
1.系统设计 此次基于单片机的自动循迹小车的设计系统,结合循迹模块来共同完成本次设计,实现小车的循迹功能,其其整体框架如图2.1所示。其中,采用STC89C52单片机来作为核心控制器,负责将各个传感器等模块链接起来&…...

linux系统中安装python到指定目录
Linux系统中安装python 下载Python源码包 根据服务器系统和需要的Python版本,在Python官网下载对应的Python源码包。 安装依赖(需要权限) yum install gcc gcc-c patch libffi-devel python-devel zlib-devel bzip2-devel openssl-devel…...
分布式事务 - seata安装
分布式事务 - seata 一、本地事务与分布式事务 1.1、本地事务 本地事务,也就是传统的单机事务。在传统数据库事务中,必须要满足四个原则(ACID)。 1.2、分布式事务 分布式事务,就是指不是在单个服务或单个数据库架构…...
CentOS to 浪潮信息 KeyarchOS 迁移体验与优化建议
浪潮信息KeyarchOS简介 KeyarchOS即云峦操作系统(简称KOS), 是浪潮信息研发的一款面向政企、金融等企业级用户的 Linux 服务器操作系统。它基于Linux内核、龙蜥等开源技术,支持x86、ARM 等主流架构处理器,其稳定性、安全性、兼容性和性能等核心能力均已…...

Go解析soap数据和修改其中数据
一、解析soap数据 package main import ("fmt" "encoding/xml" ) type Envelope struct { XMLName xml.Name Header Header } type Header struct { XMLName xml.Name xml:"Header" Security Security xml:"Security" } type Secu…...

LeetCode98. Validate Binary Search Tree
文章目录 一、题目二、题解 一、题目 Given the root of a binary tree, determine if it is a valid binary search tree (BST). A valid BST is defined as follows: The left subtree of a node contains only nodes with keys less than the node’s key. The right sub…...

【LeetCode】206. 反转链表
206. 反转链表 难度:简单 题目 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例 1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1]示例 2: 输入:head [1,2] 输…...

飞天使-通过GET 和POST进案例演示
文章目录 GETPOST GET def index(request):# 在url中获取学号sno request.GET.get("sno", None)print("学号为:",sno)# 判断学号如果有值,执行查询if sno:results get_student_by_sno(sno)# 展示在页面return render(request, ind…...
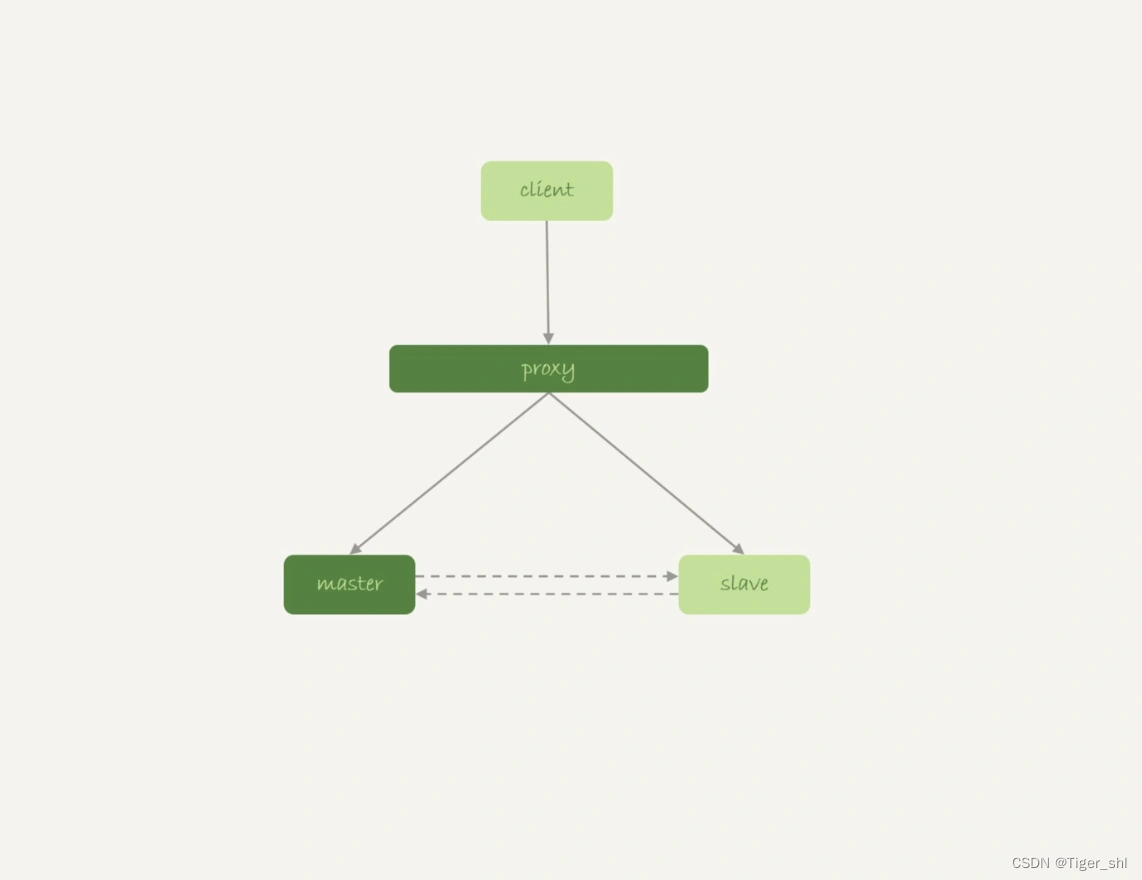
【MySql】12- 实践篇(十)
文章目录 1. 为什么临时表可以重名?1.1 临时表的特性1.2 临时表的应用1.3 为什么临时表可以重名?1.4 临时表和主备复制 2. MySql内部临时表使用场景2.1 union 执行流程2.2 group by 执行流程2.3 group by 优化方法 -- 索引2.4 group by 优化方法 -- 直接排序 3. Me…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
