【数据结构】图的简介(图的逻辑结构)
一.引例(哥尼斯堡七桥问题)
哥尼斯堡七桥问题是指在哥尼斯堡市(今属俄罗斯)的普雷格尔河(Pregel River)中,是否可以走遍每座桥一次且仅一次,最后回到起点的问题。这个问题被认为是图论的开端,也是数学史上著名的问题之一。
欧拉在解决这个问题时,将问题转化为了图论中的欧拉回路问题。他证明了如果一个图中有欧拉回路,那么这个图中每个顶点的度数都是偶数。反之,如果每个顶点的度数都是偶数,那么这个图中就存在欧拉回路。
因此,哥尼斯堡七桥问题的答案是否定的,因为哥尼斯堡的地图中有两个岛屿,这两个岛屿与其他地区相连的桥的数量都是奇数,因此这个图中不存在欧拉回路。
二.图的逻辑结构
1.图的定义
图是由顶点的有穷非空集合和顶点之间边的几何组成。
通常表示为:G=(V,E)
注:
1)G表示一个图
2)V是图G中顶点的集合
3)E是图G中顶点之间边的集合
4)在线性表中,元素的个数可以为0,称之为空表;在树中,元素的个数可以为0,称之为空树;但是在图中,顶点个数不能为0,可以没有边。
2.有向图与无向图
若顶点vi和vj之间的边没有方向,则称这条边为无向边,表示为(vi,vj)
如果图的任意两个顶点之间的边都是无向边,则称该图为无向图。
若顶点vi和vj之间的边有方向,则称这条边为有向边,表示为<vi,vj>
如果图的任意两个顶点之间的边都是有向边,则称该图为有向图。
3.图的基本术语
1)简单图
在图中,若不存在顶点到自身的边,且同一条边不重复出现。
注:数据结构中讨论的都是简单图
2)邻接/依附
无向图中,对于任意两个顶点vi和vj,若存在边(vi,vj),则称顶点vi和顶点vj互为邻接点,同时称边(vi,vj)依附于顶点vi和顶点vj。
有向图中,对于任意两个顶点vi和vj,若存在弧<vi,vj>,则称顶点vi邻接到顶点vj,顶点vj邻接自顶点vi,同时称弧<vi,vj>依附于顶点vi和顶点vj。
3)无向完全图/有向完全图
无向完全图:
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。
含有n个顶点的无向完全图中边的个数:
n*(n-1)/2
有向完全图:
在有向图中,如果任意两个顶点之间都存在方向相反的两条弧,则称该图为有向完全图。
含有n个顶点的有向完全图中边的个数:
n*(n-1)
4)稀疏图/稠密图
稀疏图:边数很少的图
稠密图:边数很多的图
5)度
无向图:TD(v)
入度:ID(v)
出度:OD(v)
6)度与边数的关系
所有顶点的度之和=边数*2
入度=出度=边数
7)权/网
权:对边赋予的有意义的数值量
(从一个顶点到另一个顶点所需要付出的代价)
网:边上带权的图
8)路径长度
非带权图:边的个数
带权图:各边权之和
9)简单回路
除了第一个顶点和最后一个顶点外,其余顶点不重复出现的回路。
10)连通图
图中任意两个顶点都是联通的
11)连通分量
非连通图的极大连通子图
12)强连通图
在有向图中,堆图中任意一对顶点vi和vj(i!=j),若从顶点vi到顶点vj和从顶点vj到顶点vi均有路径
13)生成树
n个顶点的连通图G的生成树是包含G中全部顶点的一个极小连通子图
含有n-1条边
生成树不是唯一的
14)生成森林
在非连通图中,由每个连通分量都可以得到一棵生成树,这些连通分量的生成树就组成了一个非连通图的生成森林。
4.不同结构中逻辑关系的对比
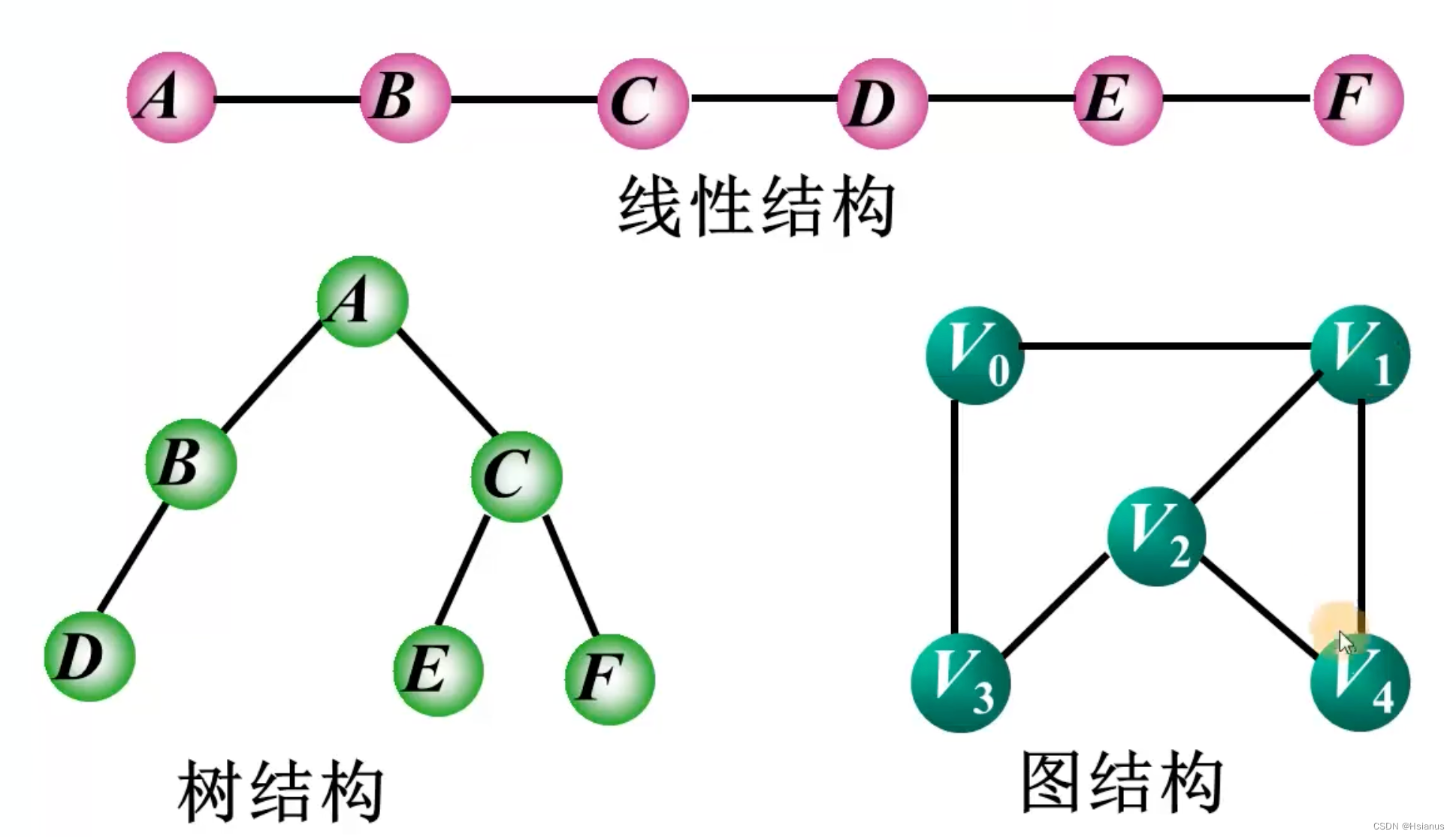
在线性结构中,数据元素之间仅具有线性关系。
在树结构中,结点之间具有层次关系。
在图结构中,任意两个顶点之间都可能有关系。
在线性结构中,元素之间的关系为前驱和后继。
在树结构中,结点之间的关系为双亲和孩子。
在图结构中,顶点之间的关系为邻接。
三.图的抽象数据类型定义
ADT Graph
Data
顶点的有穷非空集合和边的集合
Operation
初始
销毁
深度优先搜索
广度优先搜索
相关文章:

【数据结构】图的简介(图的逻辑结构)
一.引例(哥尼斯堡七桥问题) 哥尼斯堡七桥问题是指在哥尼斯堡市(今属俄罗斯)的普雷格尔河(Pregel River)中,是否可以走遍每座桥一次且仅一次,最后回到起点的问题。这个问题被认为是图…...

2342.数位和相等数对的最大和
题目来源: leetcode题目,网址:2342. 数位和相等数对的最大和 - 力扣(LeetCode) 解题思路: 哈希表,根据数位和分组后,计算每组中最大两个数之和,然后返回最大值即可。…...

关于Spring Bean的一些总结
一、Spring Bean的生命周期 Spring中的Bean生命周期是指一个Bean从被创建、初始化,到被使用,再到被销毁的整个过程。在Spring容器管理的Bean中,生命周期的管理主要通过回调方法和事件监听来实现。以下是Spring Bean的生命周期的主要阶段和回…...
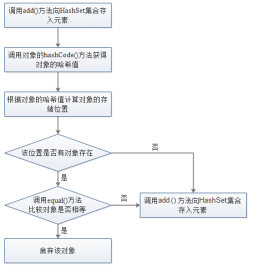
6.2 List和Set接口
1. List接口 List接口继承自Collection接口,List接口实例中允许存储重复的元素,所有的元素以线性方式进行存储。在程序中可以通过索引访问List接口实例中存储的元素。另外,List接口实例中存储的元素是有序的,即元素的存入顺序和取…...

2023数维杯国际赛数学建模D题完整论文分享!
大家好,终于完成了2023年第九届数维杯国际大学生数学建模挑战赛D题The Mathematics of Laundry Cleaning(洗衣清洁的数学原理)的完整论文啦。 D论文共43页,一些修改说明10页,正文25页,附录8页。 D题第一问…...
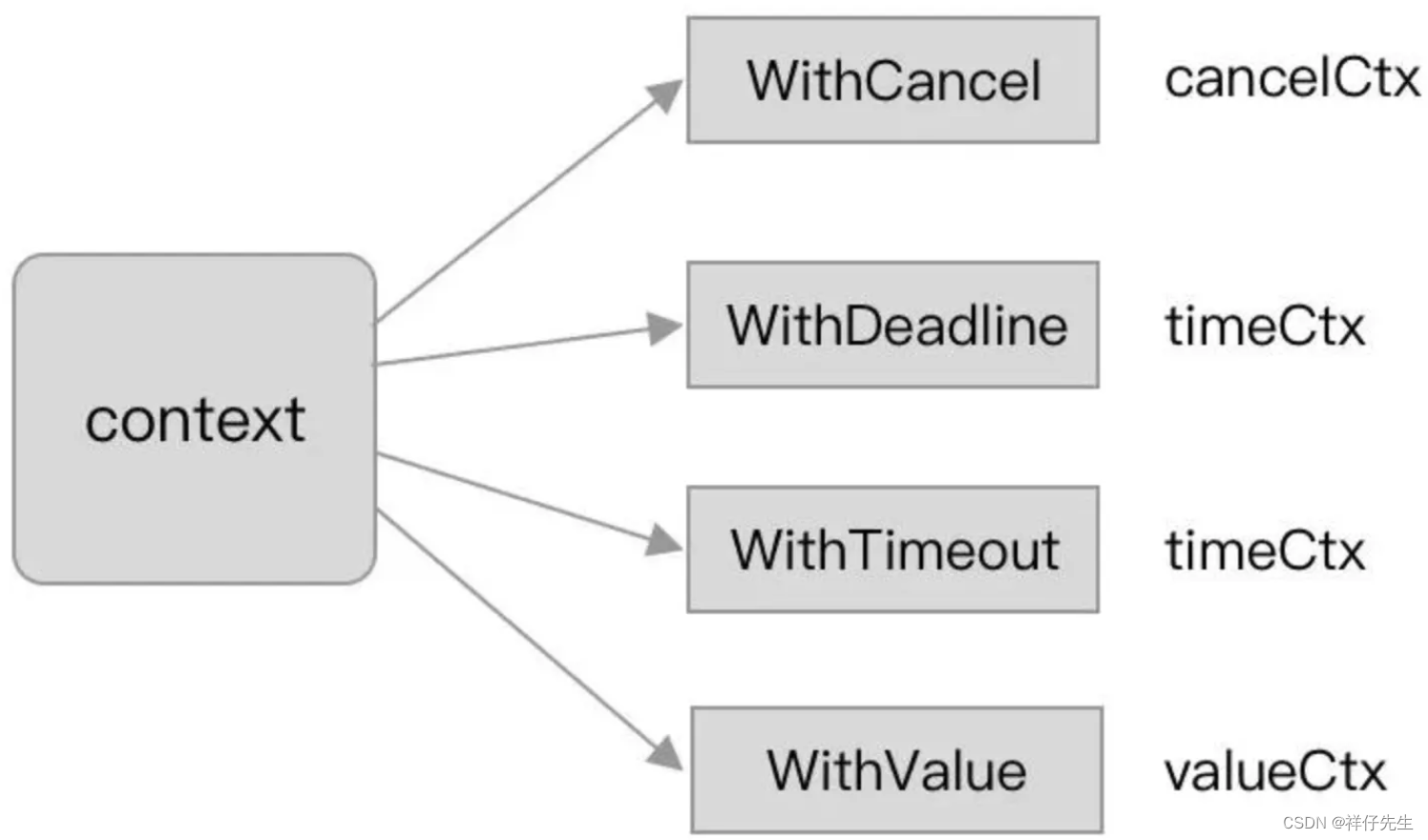
golang中context使用总结
一、context使用注意事项 在使用context时,有一些需要注意的事项,以及一些与性能优化相关的建议: 避免滥用context传递数据:context的主要目的是传递请求范围的数据和取消信号,而不是用于传递全局状态或大量数据。滥用…...
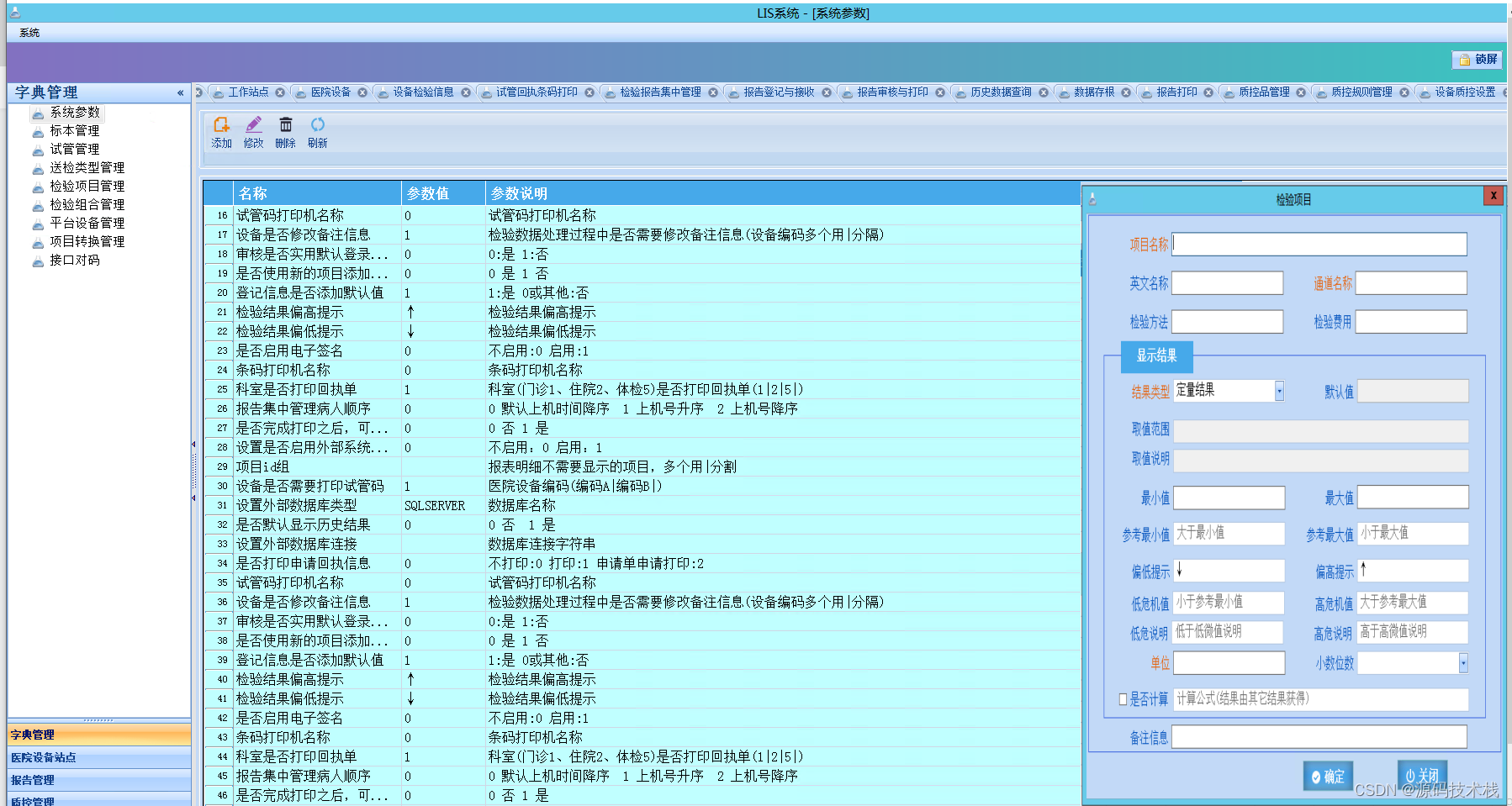
医院数字化LIS(检验信息系统)源码
临床检验信息管理系统(LIS)是利用计算机连接医疗设备,通过计算机信息处理技术,将医院检验科或实验室的临床检验数据进行自动收集、存储、处理、提取、传输和交换,满足所有授权用户的功能需求。 一、系统概述 1.LIS&am…...

挑战单芯片NOA,这款“All in one”方案或将改变主流市场走向
随着降本增效、电子架构升级(尤其是跨域计算、多域融合等概念)以及供应链减复(降低电子物料的SKU)的需求愈加明确,对于车载计算赛道,也带来新的变化。 比如,去年9月,英伟达率先发布下…...

CODING DevOps产品认证笔记
1.敏捷&精益&瀑布概述 1.1 敏捷软件开发 第一章敏捷软件开发背景 背景:乌卡时代 易变性:当今世界的变化越来越多越来越快,越来越不可预测。不确定性:历史上的任何一个时代所带来的经验已经无法为当今世界的所有变化提供参照。复杂性:事物间的…...

信息系统项目管理师 第四版 第5章 信息系统工程
1.软件工程 1.1.架构设计 1.2.需求分析 1.3.软件设计 1.4.软件实现 1.5.部署交互 1.6.过程管理 2.数据工程 2.1.数据建模 2.2.数据标准化 2.3.数据运维 2.4.数据开发利用 2.5.数据库安全 3.系统集成 3.1.集成基础 3.2.网络集成 3.3.数据集成 3.4.软件集成 3.…...

对话芯动科技 | 助力云游戏 4K级服务器显卡的探索与创新
2021年芯动科技推出了基于IMG BXT GPU IP的风华1号显卡。单块风华1号显卡可在台式机和云游戏中实现4K级别的性能,渲染能力达到5 TFLOPS,如果在服务器中同时运行两块显卡,性能还可翻倍。该显卡是为不断扩大的安卓云游戏市场量身定制的…...

[HTML]Web前端开发技术1,meta,HBuilder等——喵喵画网页
希望你开心,希望你健康,希望你幸福,希望你点赞! 最后的最后,关注喵,关注喵,关注喵,大大会看到更多有趣的博客哦!!! 喵喵喵,你对我真的…...

网上申请的电信卡能用多长时间?可以长期使用吗?
我们在网上总能看到一些关于流量卡的广告,都是19元,29元100多g的套餐,乍一看这些套餐非常便宜,但是小编提醒大家一定要注意优惠期。 网上的流量卡套餐,都是由基础套餐额外赠送充值送话费等内容组成,…...

交换机的工作原理
局域网交换技术是数据链路层上的技术,就是转发数据帧。在数据通信中,所有交换设备都执行两个基本操作: 交换数据帧生成并维护交换地址表 交换数据帧 交换机根据数据帧的MAC地址(物理地址)进行数据帧的转发操作。交换…...
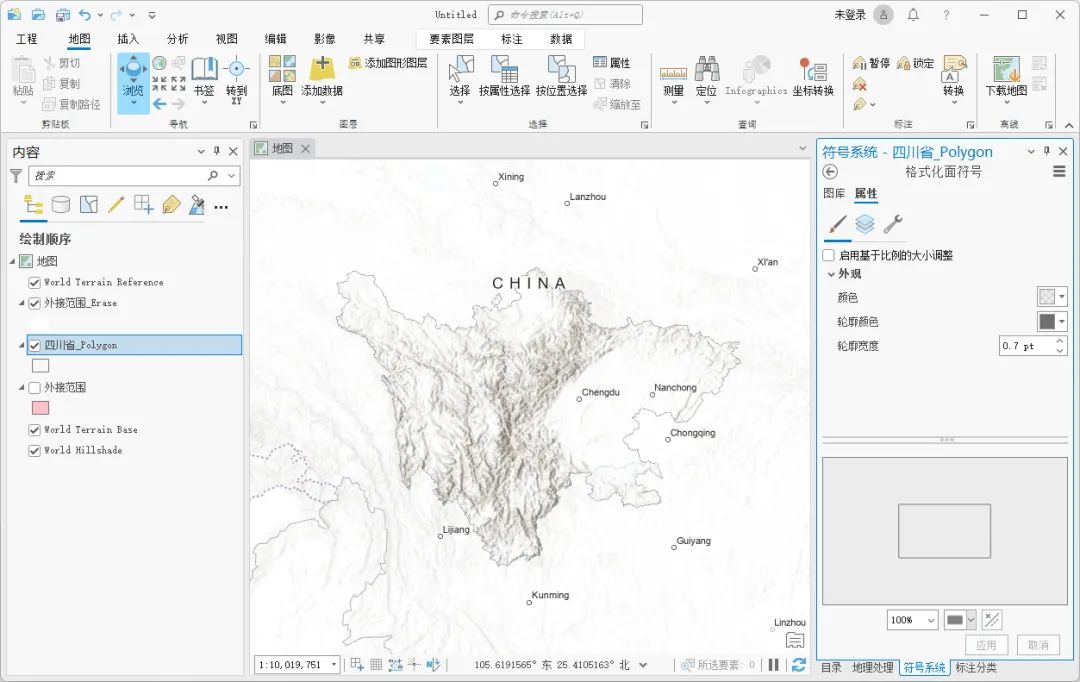
如何使用ArcGIS Pro制作粉饰效果
在地图上,如果某个部分比较重要,直接的制图不能将其凸显出来,如果想要突出显示重要部分,可以通过粉饰效果来实现,这里为大家介绍一下方法,希望能对你有所帮助。 数据来源 本教程所使用的数据是从水经微图…...

CSS滚动捕获 scroll-snap-align
CSS滚动捕获 scroll-snap-align 看到 align, 就条件反射想到对齐方式, 嗯猜对了. 不过要先看一下若干名词介绍 scroll-snap-align 指定了盒子的 snap position, 即盒子 snap area 和滚动容器的 snapport 的对齐方式. 这个属性是定义在滚动元素上, 而不是滚动容器上 语法 这个…...
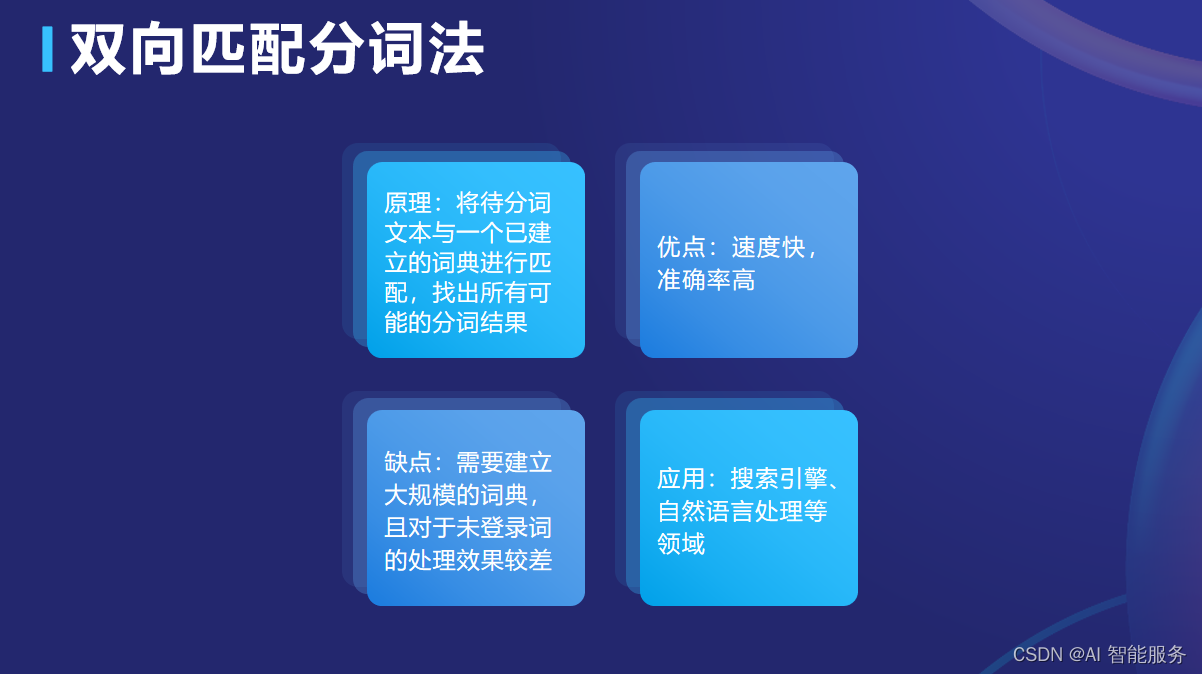
基础课8——中文分词
中文分词指的是将一个汉字序列切分成一个一个单独的词。分词就是将连续的字序列按照一定的规范重新组合成词序列的过程。在英文的行文中,单词之间是以空格作为自然分界符的,而中文只是字、句和段能通过明显的分界符来简单划界,唯独词没有一个…...

OpenHarmony应用开发入门教程(一、开篇)
前言 华为正式宣布2024年发布的华为鸿蒙OS Next版将不再兼容安卓系统。这一重大改变,预示着华为鸿蒙OS即将进入一个全新的阶段。 都说科技无国界,这是骗人的鬼话。谷歌的安卓12.0系统早已发布,但是自从受到美影响,谷歌就拒绝再向…...

vue侦听器详解及代码
在 Vue 中,我们可以使用侦听器(watcher)来监听数据的变化,并在数据发生变化时执行相应的操作。Vue 提供了 watch 选项来定义侦听器,并可以使用 vm.$watch 方法来创建侦听器。 下面是一个简单的示例,我们监…...

Python爬虫的七个常用技巧总结,这些你一定得知道!
文章目录 前言1、基本抓取网页2、使用代理IP3、Cookies处理4、伪装成浏览器5、验证码的处理6、gzip压缩7、多线程并发抓取关于Python技术储备一、Python所有方向的学习路线二、Python基础学习视频三、精品Python学习书籍四、Python工具包项目源码合集①Python工具包②Python实战…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...
