【算法-哈希表2】快乐数 和 两数之和
今天,带来哈希表相关算法的讲解。文中不足错漏之处望请斧正!
理论基础点这里
1. 快乐数
分析题意
出题者已经把题意明确告诉我们了:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
题意转化
怎么理解?
如果我们替换平方和的过程中, 发现当前的数字之前已经出现过, 那我们就陷入了无限循环.
如果没有把题意转化过来, 就会手足无措了.
解决思路
那我们只需要不断重复替换平方和的过程, 再同时判断平方和之前是否出现过:
- 没出现过: 继续重复替换
- 出现过: 陷入无限循环, 结束
编程实现
取每位上的数
关于取十进制数上的每位, 可以再谈谈.
如, 要取1234中的每位数.
1234 % 10 = 4 //取到最后一位
1234 /= 10; //去掉最后一位
123 % 10 = 3 //取到倒数第二位
123 /= 10; //去掉最后一位
12 % 10 = 4 //取到倒数第三位
12 /= 10; //去掉最后一位
1 % 10 = 4 //取到倒数第四位
1 /= 10; //去掉最后一位
//最终1234变为0,结束
如果是二进制, 八进制, 只需要mod8即可.
class Solution {
public:// 可能替换的过程可能一直循环:// 如果当前得到的数之前已经得到过, 则会无限循环; 反之不会bool isHappy(int n) {unordered_set<int> appearedNum;while (n != 1) {int sum = getSqureSum(n);// 只要当前的数之前没出现过, 就代表可能这个数能变到1if (appearedNum.find(sum) == appearedNum.end()) {appearedNum.insert(sum);} else { // 反之不可能变到1return false;}n = sum;}return true;}
private:int getSqureSum(int n) {int sum = 0;while (n) {sum += pow(n % 10, 2);n /= 10;}return sum;}
};
2. 两数之和
分析题意
*很好理解, 无需分析.
题意转化
找到 x 和 y, 满足 x + y = target.
解决思路
一层遍历获取 x, 查找nums内是否有这样的 y 满足 y = target - x.
关于查找:
- for暴力查找 – O(n)
- 哈希快速查找 – O(1)
查找某个元素在某个集合中是否用过, 这是哈希的绝活; 而且题目要求返回下标. 综合这两点, 我们用 unordered_map, 存储键值对的哈希表.
编程实现
class Solution {
public:// 找到 x 和 y, 满足 x + y = targetvector<int> twoSum(vector<int>& nums, int target) {unordered_map<int, int> numsMap; // <value, index>// 一层遍历获取 x, 查找nums内是否有这样的 y 满足 y = target - xfor (int i = 0; i < nums.size(); ++i) {int x = nums[i];int y = target - x;auto iter = numsMap.find(y);if (iter != numsMap.end()) {int i1 = i;int i2 = iter->first;return {i, iter->second};} else {numsMap.insert(pair<int, int>(nums[i], i));}}return {};}
};
今天的分享就到这里了,感谢您能看到这里。
这里是培根的blog,期待与你共同进步!
相关文章:

【算法-哈希表2】快乐数 和 两数之和
今天,带来哈希表相关算法的讲解。文中不足错漏之处望请斧正! 理论基础点这里 1. 快乐数 分析题意 出题者已经把题意明确告诉我们了: 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程直到这个数变为 1&am…...

MR外包团队:MR、XR混合现实技术应用于游戏、培训,心理咨询、教育成为一种创新的各行业MR、XR形式!
随着VR、AR、XR、MR混合现实等技术逐渐应用于游戏开发、心理咨询、培训、教育各个领域,为教育、培训、心理咨询等行业带来了全新的可能性。MR、XR游戏开发、心理咨询是利用虚拟现实技术模拟真实场景,让学生身临其境地参与学习和体验,从而提高…...

【P1008 [NOIP1998 普及组] 三连击】
[NOIP1998 普及组] 三连击 题目背景 本题为提交答案题,您可以写程序或手算在本机上算出答案后,直接提交答案文本,也可提交答案生成程序。 题目描述 将 1 , 2 , … , 9 1, 2, \ldots , 9 1,2,…,9 共 9 9 9 个数分成 3 3 3 组ÿ…...
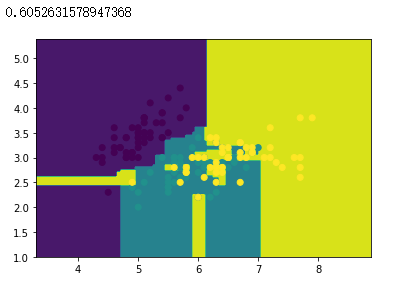
机器学习算法——集成学习
目录 1. Bagging 1. Bagging Bagging(bootstrap aggregating:自举汇聚法)也叫装袋法,其思想是通过将许多相互独立的学习器的结果进行结合,从而提高整体学习器的泛化能力,是一种并行集成学习方法。 工作流…...
java springboot在当前测试类中添加临时属性 不影响application和其他范围
目前 我们的属性基本都写在 application.yml 里面了 但是 如果 我们只是想做一下临时变量的测试 有没有办法实现呢? 显然是有的 这里 我们还是先在application.yml中去写一个 test属性 下面加个prop 然后 我们尝试在测试类中 获取一下这个属性 直接用 Value 读取…...

原型网络Prototypical Network的python代码逐行解释,新手小白也可学会!!由于工作量大,准备整8个系列完事,-----系列5
文章目录 前言一、原始程序---计算原型,开始训练,计算损失二、每一行代码的详细解释2.1 粗略分析2.2 每一行代码详细分析 前言 承接系列4,此部分属于原型类中的计算原型,开始训练,计算损失函数。 一、原始程序—计算原…...

milvus数据库的数据管理-插入数据
一、插入数据 1.准备数据 数据必须与数据库中定义的字段元数据一致,与集合的模式匹配 import random data [[i for i in range(2000)],[str(i) for i in range(2000)],[i for i in range(10000, 12000)],[[random.random() for _ in range(2)] for _ in range(2…...
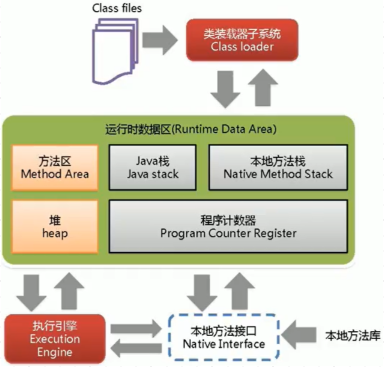
系列一、请谈谈你对JVM的理解?Java8的虚拟机有什么更新?
一、请谈谈你对JVM的理解?Java8的虚拟机有什么更新? JVM是Java虚拟机的意思。它是建立在操作系统之上的,由类加载器子系统、本地方法栈、Java栈、程序计数器、方法区、堆、本地方法库、本地方法接口、执行引擎组成。 (1࿰…...

恕我直言,大模型对齐可能无法解决安全问题,我们都被表象误导了
是否听说过“伪对齐”这一概念? 在大型语言模型(LLM)的评估中,研究者发现了一个引人注目的现象:当面对多项选择题和开放式问题时,模型的表现存在显著差异。这一差异根源在于模型对复杂概念的理解不够全面&…...

Apache Airflow (九) :Airflow Operators及案例之BashOperator及调度Shell命令及脚本
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你大数据的个人空间-豹…...
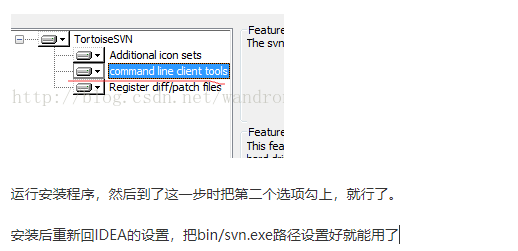
IJ中配置TortoiseSVN插件:
文章目录 一、报错情况:二、配置TortoiseSVN插件: 一、报错情况: 由于公司电脑加密,TortoiseSVN菜单没有提交和更新按钮,所以需要使用IJ的SVN进行代码相关操作 二、配置TortoiseSVN插件: 需要设置一个svn.…...

个人实现在线支付,一种另类的在线支付解决方案
Hi, I’m Shendi 个人实现在线支付,一种另类的在线支付解决方案 个人实现在线支付的方式 对于在线支付,最多的是接入微信与支付宝。但都需要营业执照,不适用于个人。 当然,可以去办理一个个体工商户,但对我这种小额收…...

浅谈智能安全配电装置应用在银行配电系统中
【摘要】银行是国家重点安全保护部分,关系到社会资金的稳定,也是消防重点单位。消防安全是银行工作的重要组成部分。在银行配电系统中应用智能安全配电装置,可以提高银行的智能控制水平,有效预防电气火灾。 【关键词】银行&#…...
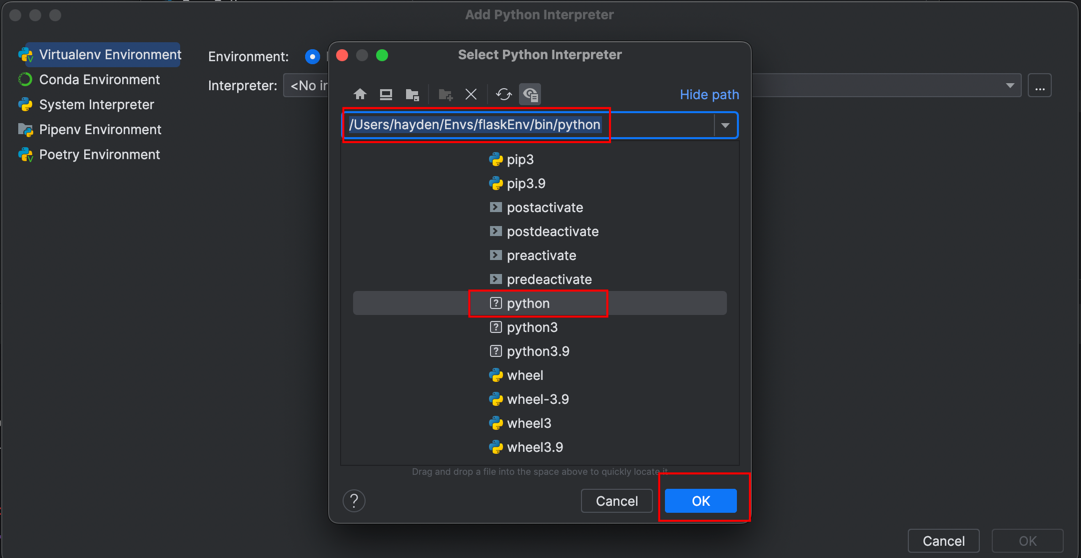
macOS下如何使用Flask进行开发
👨🏻💻 热爱摄影的程序员 👨🏻🎨 喜欢编码的设计师 🧕🏻 擅长设计的剪辑师 🧑🏻🏫 一位高冷无情的编码爱好者 大家好,我是全栈工…...
记一次服务器配置文件获取OSS
一、漏洞原因 由于网站登录口未做双因子校验,导致可以通过暴力破解获取管理员账号,成功进入系统;未对上传的格式和内容进行校验,可以任意文件上传获取服务器权限;由于服务器上配置信息,可以进一步获取数据库权限和OSS管理权限。二、漏洞成果 弱口令获取网站的管理员权限通…...

合众汽车选用风河Wind River Linux系统
导读合众新能源汽车股份有限公司近日选择了Wind River Linux 用于开发合众智能安全汽车平台。 合众智能安全汽车平台(Hozon Automo-tive Intelligent Security Vehicle Plat-form)是一个面向高性能服务网关及车辆控制调度的硬件与软件框架,将于2024年中开始投入量产…...
)
PTA平台-2023年软件设计综合实践_5(指针及引用)
第一题 6-1 调和平均 - C/C 指针及引用 函数hmean()用于计算整数x和y的调和平均数,结果应保存在指针r所指向的浮点数对象中。当xy等于0时,函数返回0表示无法计算,否则返回1。数学上,两个数x和y的调和平均数 z 2xy/(xy) 。 直接…...

智慧卫生间
智慧卫生间 获取ApiKey/SecretKey获取Access_token获取卫生间实时数据返回说明 获取ApiKey/SecretKey ApiKey/SecretKey采用 线下获取的方式,手动分配。 获取Access_token 向授权服务地址http://xxxxxx:12345/token(示意)发送post请求,并在data中带上…...
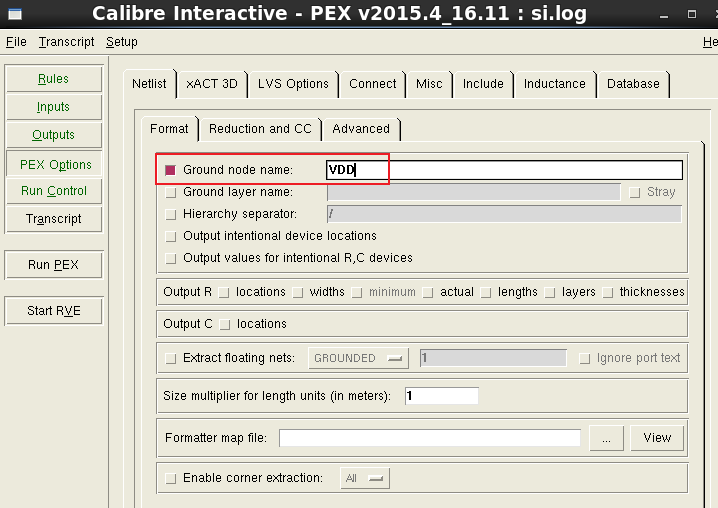
Cadence virtuoso drc lvs pex 无法输入
问题描述:在PEX中的PEX options中 Ground node name 无法输入内容。 在save runset的时候也出现无法输入名称的情况 解决办法: copy一个.bashrc文件到自己的工作目录下 打开.bashrc文件 在.bashrc中加一行代码:unset XMODIFIERS 在终端sour…...
, 分析调用链, 编写POC)
反序列化漏洞(2), 分析调用链, 编写POC
反序列化漏洞(2), 反序列化调用链分析 一, 编写php漏洞脚本 http://192.168.112.200/security/unserial/ustest.php <?php class Tiger{public $string;protected $var;public function __toString(){return $this->string;}public function boss($value){eval($valu…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
