Win10安装mediapipe的步骤
我之前想自己安装mediapipe包进行人体检测的学习，但整了好几个月都不行，这次终于让我整好了，我的python版本为python = 3.7.1。
注意，不要直接用pip install mediapipe 进行安装，我之前这样安装的，mediapipe安装好了，但是所需要的opencv-contrib-python安装失败。
一、安装mediapipe
首先安装opencv-contrib-python
pip install opencv-contrib-python -i https://pypi.douban.com/simple/，但安装失败，
在https://pypi.tuna.tsinghua.edu.cn/simple/opencv-contrib-python/中下载对应的版本，我下载的是opencv_contrib_python-3.4.10.35-cp37-cp37m-win_amd64.whl
然后再pycharm的控制端输入，必须把opencv_contrib_python-3.4.10.35-cp37-cp37m-win_amd64.whl放在你终端对应的路径，之后运行
pip install opencv_contrib_python-4.5.5.62-cp36-abi3-win_amd64.whl
就安装好了。
安装mediapipe
pip install mediapipe
经过这两步mediapipe就安装好了
二、其他的报错
TypeError: create_bool(): incompatible function arguments.
The following argument types are supported:
1. (arg0: bool) -> mediapipe.python._framework_bindings.packet.Packet
那么这个问题就是你所使用的第三方库发生了变动，可能是添加了新的功能**，需要减少或者添加参数**，而我的原因就是由于mediapipe更新之后对于mediapipe.solutions.pose.Pose类的调用需要添加一个参数enable_segmentation
相关文章：
Win10安装mediapipe的步骤
我之前想自己安装mediapipe包进行人体检测的学习，但整了好几个月都不行，这次终于让我整好了，我的python版本为python 3.7.1。注意，不要直接用pip install mediapipe 进行安装，我之前这样安装的，mediapipe安…...
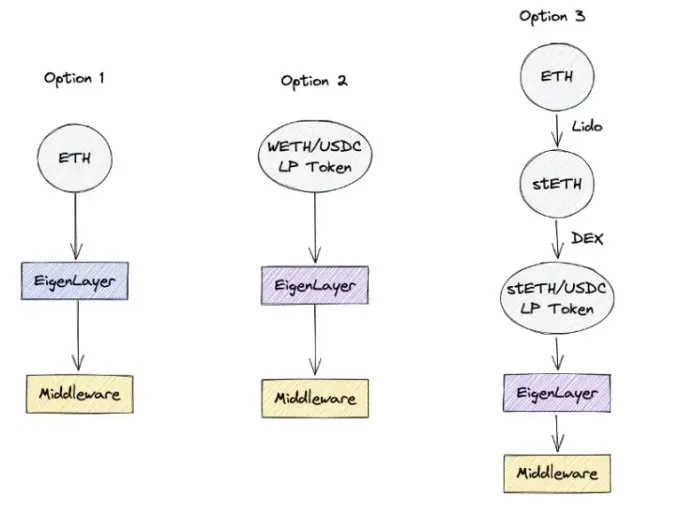
项目调研丨以太坊再质押项目EigenLayer白皮书四大看点（内附完整版中文白皮书）
北京时间2月21日下午，被众多一线投研机构视为2023年以太坊最重要的创新，有可能开启以太坊新叙事方向的项目Eigenlayer终于披露了其第一版白皮书。EigenLayer是以太坊的再质押集，允许共识层ETH质押者选择验证构建在以太坊生态系统之上的新软件…...
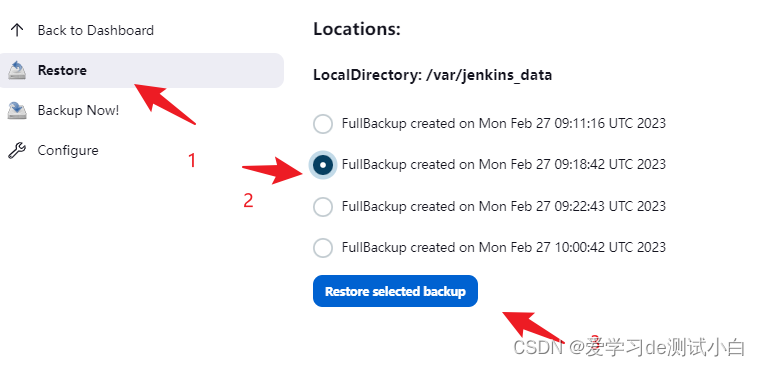
51-Jenkins-Periodic Backup插件实现Jenkins备份
Periodic Backup插件实现Jenkins备份前言目录结构插件备份安装插件使用插件前言 本篇来学习下使用Periodic Backup插件实现Jenkins备份 目录结构 Jenkins的所有数据都是存放在文件中的，所以，Jenins备份其实就是备份Jenkins_HOME目录。 Jenkins_Home目…...
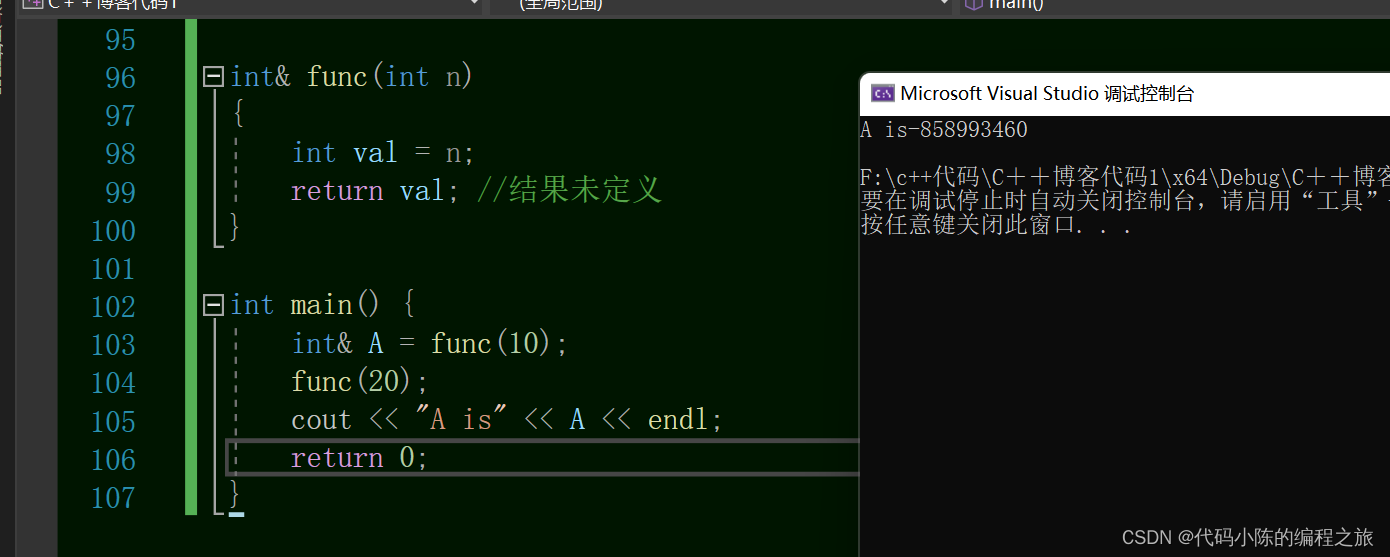
C++之入门之引用，内联函数
一、引用 1、引用的概念 在C中，引用的本质其实就是给一个已经存在的变量”起别名“。也就是说，引用与它所引用的对象共用一块空间。（同一块空间的多个名字） 就比如说，李逵又叫黑旋风，而黑旋风就是指李逵…...
linux kprobe使用
使用场景 监控某个内核函数是否被调用获取某个内核函数耗费的时间获取某个内核函数的入参获取某个内核函数的调用栈（dump_stack()）获取某个内核函数的返回值 参数传递规则 x86平台对pt_regs的定义 arch/x86/include/asm/ptrace.h // i386架构 #ifdef…...
2023年超全前端面试题-背完稳稳拿offer（欢迎补充）
HTML、CSS相关 HTML5 HTML5新特性 增强了表单，input新增了一些type： color----定义调色板 tel-----定义包含电话号码的输入域 email—定义包含email地址的输入域 search–定义搜索域 number–定义包含数值的输入域 date----定义选取日、月、年的输入域…...
python之web自动化测试框架
梳理下搭建web自动化框架的流程： 创建目录： cases：存放测试用例，unittest框架要求用例名必须以test开头，所以命名test_case.py test_case.py代码如下：继承unittest.TestCase类下面的方法setupclass(),te…...
算法笔记（十五）—— 动态规划（暴力递归到动态规划）习题训练！
通过递归到记忆化搜索再到严格表结构的动态规划 递归方法的评价：1. 单可变参数的维度；2. 可变参数的个数 记忆化搜索 在暴力递归中会存在很多的重复计算，可以使用存储结构来实现空间换时间。 严格表结构的动态规划 整理位置之间的依赖关系…...
云原生架构基础概念及应用办法
什么是云原生？ 云原生是一种基于容器、微服务和自动化运维的软件开发和部署方法。它可以使应用程序更加高效、可靠和可扩展，适用于各种不同的云平台。 如果要更直接通俗的来解释下上面的概念。 云原生更准确来说就是一种文化，是一种潮流&a…...
RedisTemplate 的基本使用手把手教
下载实例源码 使用步骤 1、引入 spring-boot-starter-data-redis 依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId> </dependency>2、在 application.yml 配置 R…...
Hbase -- Compact工具梳理
1. 背景 当前，线上HBase集群的自动Major Compact是关闭的，我们选择在凌晨业务空闲的时候进行手动触发Major Compact，Compact工具就是在运维平台上对资源组、RS、表进行Major Compact。目前线上有2种版本的Compact程序：Compact_v1…...
【java代码审计】SQL注入
1 原理 没有正确的对用户的输入进行检查，将用户的输入以拼接的方式带入到SQL语句中，导致SQL注入。 2 产生SQL注入的原因 2.1 JDBC拼接不当造成SQL注入 前置知识： JDBC执行SQL语句的两种方式： PrepareStatement：会对…...
前置知识-辛 Runge-Kutta 方法
1.3.3 辛 Runge-Kutta 方法 将方程 ( 1.10.2 ) (1.10 .2) (1.10.2) 改写为 d z d x =...
require 与 import 两种引入模块方式到底有什么区别？
关于JavaScript 的模块化规范，可以移步至： 【JavaScript高级】模块化规范「一文让你彻底搞懂前端模块化规范 & 区别」 下面进入正题 require 与 import 两种引入模块方式，到底有什么区别呢？ 大致可以分为以下几个方面&#…...
软考信息系统监理师备考建议
用好备考方法，两三个月就可以过的。信息系统监理师备考最好以教材和历年真题为主，教学视频模拟题为辅。考试介绍与复习建议：考试设置的科目包括：（1）信息系统工程监理基础知识，考试时间150分钟&a…...
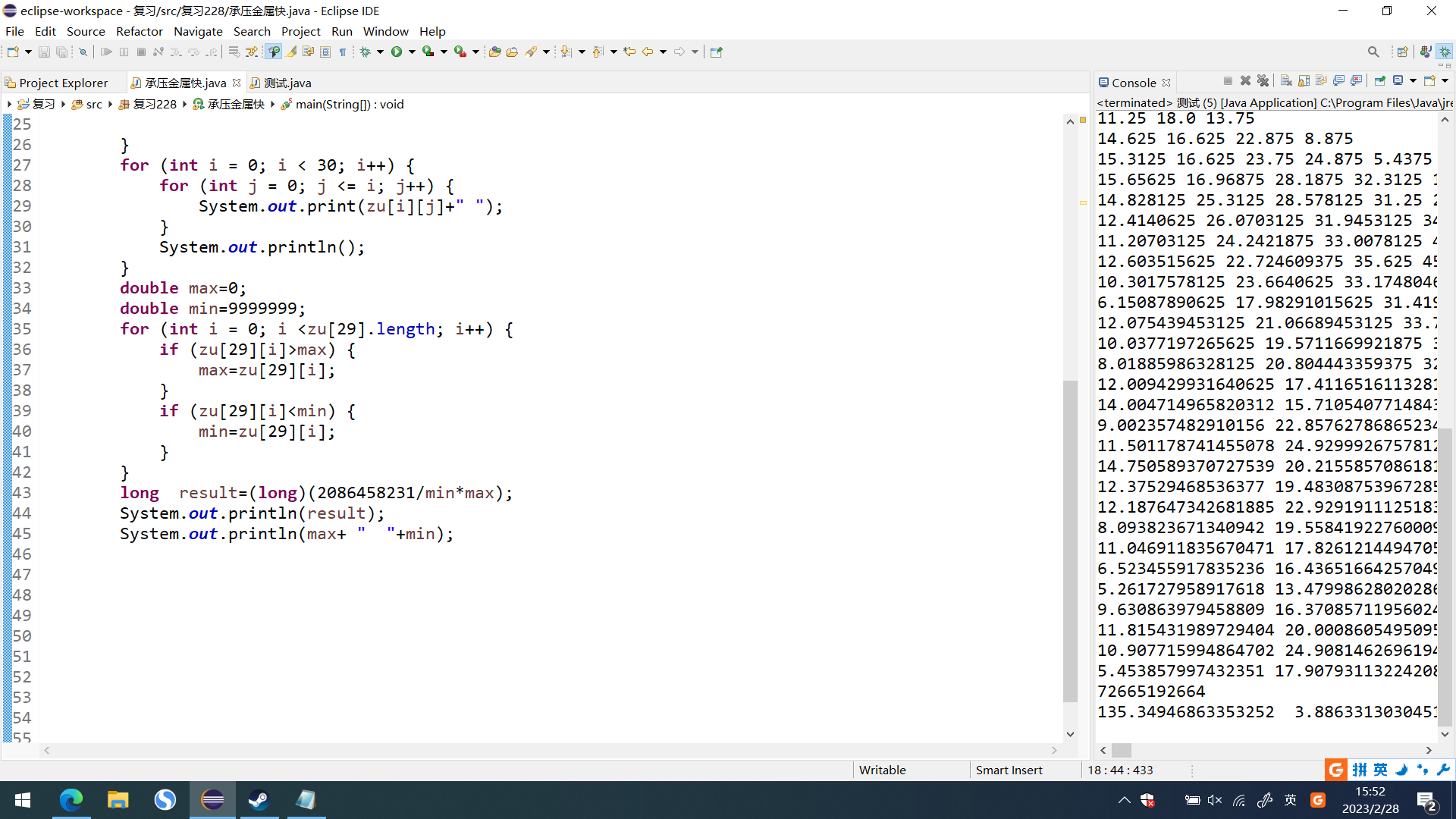
第八届蓝桥杯省赛——4承压计算（二维数组，嵌套循环）
题目：X星球的高科技实验室中整齐地堆放着某批珍贵金属原料。每块金属原料的外形、尺寸完全一致，但重量不同。金属材料被严格地堆放成金字塔形。7 5 8 7 8 8 9 2 7 2 8 1 4 9 1 8 1 8 8 4 1 7 9 6 1 4 5 4 5 6 5 5 6 9 5 6 5 5 4 7 9 3 5 5 1 7 5 7 9 7 4…...
【ECNU】3645. 莫干山奇遇（C++）
目录 题目 输入格式 输出格式 样例 提示 思路 代码 题目 单点时限: 2.0 sec 内存限制: 512 MB 出题人当然是希望出的题目有关 oxx，于是想方设法给题目配上一些有关 oxx 的背景故事，使得它看起来不那么无趣。但有的时候却无法引入合适的小姐姐&…...
为什么需要学习shell、shell的作用
课程基于B站于超课程笔记 03 Shebang的正确玩法_哔哩哔哩_bilibili P1 shell的作用 P2 shell执行命令的流程 P3 Shebang的正确玩法 什么是shell及组成 shell概念 shelll组成 Shebang概念 /bin/sh /bin/bash一样，都是指向一个bash解释器 [rootlocalhost ~]#…...
pgsql-Create_ALTER_GRANT_REVOKE命令语法
pgsql-Create_ALTER_GRANT_REVOKE命令语法 资料 语法约定 CREATE ROLE ALTER ROLE GRANT授权 REVOKE回收授权 权限类型说明 语法约定 下面的约定被用于命令的大纲：方括弧（[和]）表示可选的部分（在 Tcl 命令里，使…...
【linux】：进程概念
文章目录 冯诺依曼体系结构一：操作系统二: 进程总结冯诺依曼体系结构 我们常见的计算机，如笔记本。我们不常见的计算机，如服务器，大部分都遵守冯诺依曼体系。 冯诺依曼体系如下图： 那么输入设备有哪些呢？…...
golang循环变量捕获问题
在 Go 语言中，当在循环中启动协程（goroutine）时，如果在协程闭包中直接引用循环变量，可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下： 问题背景 看这个代码片段： fo…...
C++：std::is_convertible
C++标志库中提供is_convertible，可以测试一种类型是否可以转换为另一只类型： template <class From, class To> struct is_convertible; 使用举例： #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...
django filter 统计数量 按属性去重
在Django中，如果你想要根据某个属性对查询集进行去重并统计数量，你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求： 方法1：使用annotate()和Count 假设你有一个模型Item，并且你想…...
P3 QT项目----记事本（3.8）
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...
Cloudflare 从 Nginx 到 Pingora：性能、效率与安全的全面升级
在互联网的快速发展中，高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司，近期做出了一个重大技术决策：弃用长期使用的 Nginx，转而采用其内部开发…...
Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言，以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天，异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时，会出现小数部分被截断的情况。典型错误模式如下： void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...
在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）
考察一般的三次多项式，以r为参数： p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]； 此多项式的根为： 尽管看起来这个多项式是特殊的，其实一般的三次多项式都是可以通过线性变换化为这个形式…...
代码规范和架构【立芯理论一】（2025.06.08）
1、代码规范的目标 代码简洁精炼、美观，可持续性好高效率高复用，可移植性好高内聚，低耦合没有冗余规范性，代码有规可循，可以看出自己当时的思考过程特殊排版，特殊语法，特殊指令，必须…...