当前位置： 首页 > news >正文

react antd下拉选择框选项内容换行

news 2026/2/9 16:06:07

下拉框选项字太多，默认样式是超出就省略号，需求要换行全展示，选完在选择框里还是要省略的

.less:

.aaaDropdown {:global {.ant-select-dropdown-menu-item {white-space: pre-line !important;word-break: break-all !important;}}
}

html部分：

<Select dropdownClassName={styles.aaaDropdown}>

相关文章：

react antd下拉选择框选项内容换行

下拉框选项字太多&#xff0c;默认样式是超出就省略号&#xff0c;需求要换行全展示&#xff0c;选完在选择框里还是要省略的 .less: .aaaDropdown {:global {.ant-select-dropdown-menu-item {white-space: pre-line !important;word-break: break-all !important;}} } html…...

编程日记 2023/11/19 1:13:23

图像分类(一) 全面解读复现AlexNet

解读 论文原文&#xff1a;http://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf Abstract-摘要 翻译 我们训练了一个庞大的深层卷积神经网络&#xff0c;将ImageNet LSVRC-2010比赛中的120万张高分辨率图像分为1000个不…...

编程日记 2023/11/19 1:12:22

JAXB实现XML和Bean相互转换

目录 XML和Bean转换工具简介JAXB简介Java Bean类XMLUtil工具类 另一篇转换方式 xstream实现xml和java bean 互相转换 XML和Bean转换工具简介 Java中实现XML和Bean的转换的方式或插件有以下几种&#xff1a; JAXB&#xff08;Java Architecture for XML Binding&#xff09;&…...

编程日记 2023/11/19 1:09:19

视频剪辑技巧：简单步骤，批量剪辑并随机分割视频

随着社交媒体平台的广泛普及和视频制作需求的急剧增加&#xff0c;视频剪辑已经成为了当今社会一项不可或缺的技能。然而&#xff0c;对于许多初学者来说&#xff0c;视频剪辑可能是一项令人望而生畏的复杂任务。可能会面临各种困难&#xff0c;如如何选择合适的软件和硬件、如…...

编程日记 2023/11/19 1:08:18

Vue3-shallowRef 和 shallowReactive函数（浅层次的响应式）

Vue3-shallowRef 和 shallowReactive函数&#xff08;浅层次的响应式&#xff09; shallowRef函数 功能&#xff1a;只给基本数据类型添加响应式。如果是对象&#xff0c;则不会支持响应式&#xff0c;层成也不会创建Proxy对象。ref和shallowRef在基本数据类型上是没有区别的…...

编程日记 2023/11/19 1:07:17

ExoPlayer架构详解与源码分析（8）——Loader

系列文章目录 ExoPlayer架构详解与源码分析&#xff08;1&#xff09;——前言 ExoPlayer架构详解与源码分析&#xff08;2&#xff09;——Player ExoPlayer架构详解与源码分析&#xff08;3&#xff09;——Timeline ExoPlayer架构详解与源码分析&#xff08;4&#xff09;—…...

编程日记 2023/11/19 1:06:15

ExoPlayer架构详解与源码分析（9）——TsExtractor

系列文章目录 ExoPlayer架构详解与源码分析&#xff08;1&#xff09;——前言 ExoPlayer架构详解与源码分析&#xff08;2&#xff09;——Player ExoPlayer架构详解与源码分析&#xff08;3&#xff09;——Timeline ExoPlayer架构详解与源码分析&#xff08;4&#xff09;—…...

编程日记 2023/11/19 1:05:14

【Python 千题 —— 基础篇】输出列表方差

题目描述 题目描述 输出列表的方差。题中有一个包含数字的列表 [10, 39, 13, 48, 32, 10, 9]&#xff0c;使用 for 循环获得这个列表中所有项的方差。 输入描述 无输入。 输出描述 输出列表的方差。 示例 示例 ① 输出&#xff1a; 列表的方差是&#xff1a;228.0代码…...

编程日记 2023/11/19 1:03:12

【Spring总结】基于配置的方式来写Spring

本篇文章是对这两天所学的内容做一个总结&#xff0c;涵盖我这两天写的所有笔记&#xff1a; 【Spring】 Spring中的IoC&#xff08;控制反转&#xff09;【Spring】Spring中的DI&#xff08;依赖注入&#xff09;Dependence Import【Spring】bean的基础配置【Spring】bean的实…...

编程日记 2023/11/19 1:02:10

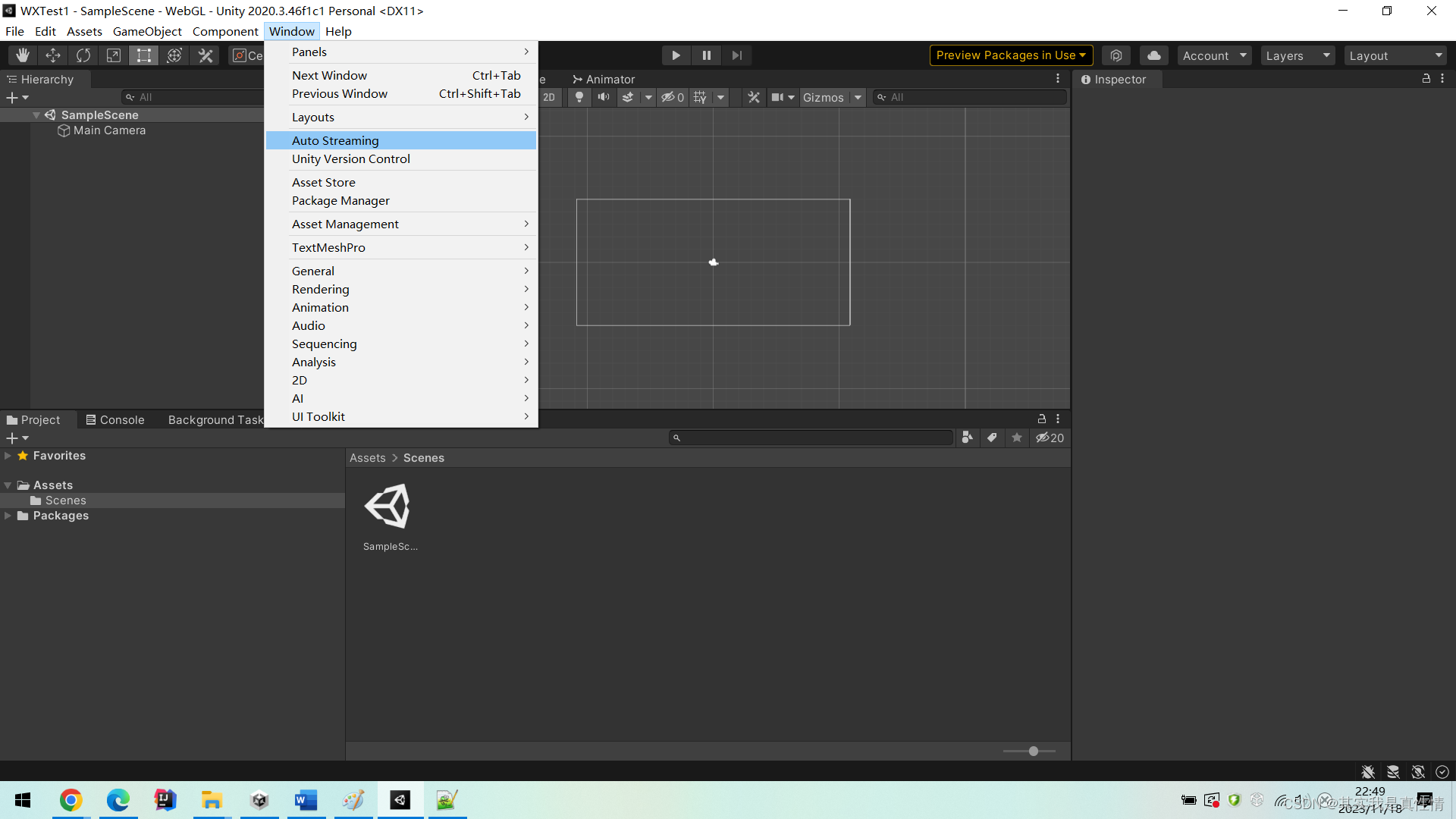
Unity在Windows选项下没有Auto Streaming

Unity在Windows选项下没有Auto Streaming Unity Auto Streaming插件按网上说的不太好使最终解决方案 Unity Auto Streaming插件 我用的版本是个人版免费版&#xff0c;版本号是&#xff1a;2021.2.5f1c1&#xff0c;我的里边Windows下看不到Auto Streaming选项,就像下边这张图…...

编程日记 2023/11/19 1:01:09

下厨房网站月度最佳栏目菜谱数据获取及分析

目录 概要 源数据获取 写Python代码爬取数据 Scala介绍与数据处理 1.Sacla介绍...

编程日记 2023/11/19 1:00:06

【Java 进阶篇】深入理解 JQuery 事件绑定：标准方式

在前端开发中&#xff0c;处理用户与页面的交互是至关重要的一部分。JQuery作为一个广泛应用的JavaScript库&#xff0c;为我们提供了简便而强大的事件绑定机制&#xff0c;使得我们能够更加灵活地响应用户的行为。本篇博客将深入解析 JQuery 的标准事件绑定方式&#xff0c;为…...

编程日记 2023/11/19 0:59:05

某app c++层3处魔改md5详解

hello everybody,本期是安卓逆向so层魔改md5教学,干货满满,可以细细品味,重点介绍的是so层魔改md5的处理. 常见的魔改md5有: 1:明文加密前处理 2:改初始化魔数 3:改k表中的值 4:改循环左移的次数 本期遇到的是124.且循环左移的次数是动态的,需要前面的加密结果处理生成 目录…...

编程日记 2023/11/19 0:58:04

安装MongoDB

查看MongoDB版本可以执行如下命令 mongod --version 如果是Ubuntu&#xff0c;则直接安装 sudo apt-get install -y mongodb如果是其他&#xff0c;比如Amazon Linux2。 查看Linux系统发行版类型 grep ^NAME /etc/*release 如果是 Amazon Linux 2&#xff0c;则创建一个r…...

编程日记 2023/11/19 0:57:03

C++加持让python程序插上翅膀——利用pybind11进行c++和python联合编程示例

目录 0、前言1、安装 pybind11库c侧python侧 2、C引入bybind11vs增加相关依赖及设置cpp中添加头文件及导出模块cpp中添加numpy相关数据结构的接收和返回编译生成dll后改成导出模块同名文件的.pyd 3、python调用c4、C引入bybind11 0、前言 在当今的计算机视觉和机器学习领域&am…...

编程日记 2023/11/19 0:56:03

ubuntu20.04安装cv2

查看ubuntu的版本 cat /etc/lsb-release DISTRIB_IDUbuntu DISTRIB_RELEASE20.04 DISTRIB_CODENAMEfocal DISTRIB_DESCRIPTION"Ubuntu 20.04.3 LTS"更改镜像源 cp /etc/apt/sources.list /etc/apt/sources.list.bak cat > /etc/apt/sources.listdeb http://mirr…...

编程日记 2023/11/19 0:54:00

Android 13.0 recovery出厂时清理中字体大小的修改

1.前言 在13.0的系统rom定制化开发中，在recovery模块也是系统中比较重要的模块，比如恢复出厂设置，recovery ota升级， 清理缓存等等，在一些1080p的设备，但是density只是240这样的设备，会在恢复出厂设置的时候，显示的字体有点小， 产品要求需要将正在清理的字体调大点，这…...

编程日记 2023/11/19 0:51:59

spring+pom-注意多重依赖时的兼容问题[java.lang.NoSuchMethodError]

背景&#xff1a; 项目中同时引入了依赖A和依赖B&#xff0c;而这两个依赖都依赖于项目C&#xff0c;但它们指定的C版本不一致&#xff0c;导致运行时出现了错误。 报错如&#xff1a; java.lang.NoSuchMethodError 解决方案&#xff1a; 需要在项目pom文件中引入依赖C并指定需…...

编程日记 2023/11/19 0:50:58

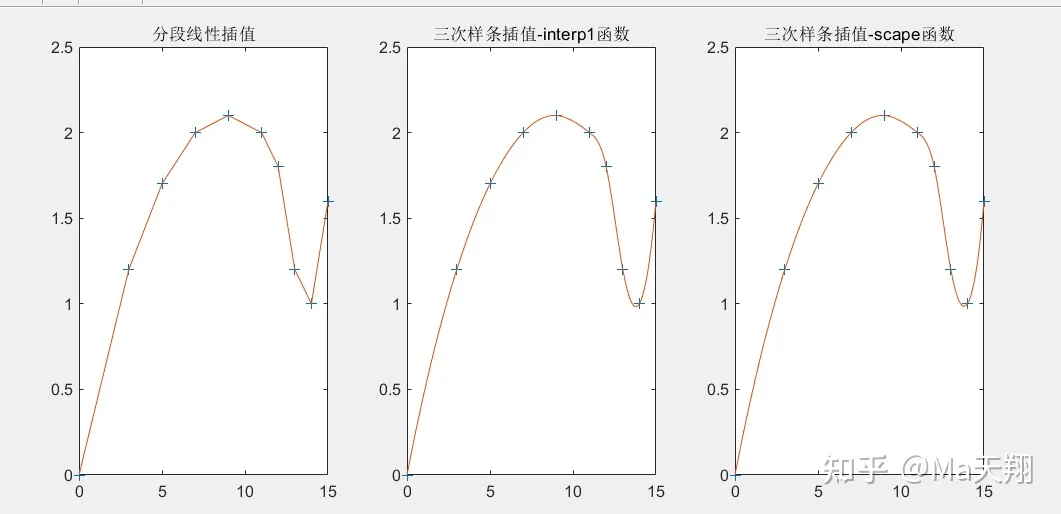
Matalab插值详解和源码

转载&#xff1a;Matalab插值详解和源码 - 知乎 (zhihu.com) 插值法 插值法又称“内插法”&#xff0c;是利用函数f (x)在某区间中已知的若干点的函数值&#xff0c;作出适当的特定函数&#xff0c;在区间的其他点上用这特定函数的值作为函数f (x)的近似值&#xff0c;这种方…...

编程日记 2023/11/19 0:49:57

Flask 接口

目录 前言 代码实现 简单接口实现 执行其它程序接口 携带参数访问接口 前言 有时候会想着开个一个接口来访问试试&#xff0c;这里就给出一个基础接口代码示例 代码实现 导入Flask模块&#xff0c;没安装Flask 模块需要进行 安装&#xff1a;pip install flask 使用镜…...

编程日记 2023/11/19 0:48:56

Chapter03-Authentication vulnerabilities

文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

编程新知 2026/2/7 4:57:53

遍历 Map 类型集合的方法汇总

1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

编程新知 2026/1/24 15:08:45

Go 语言接口详解

Go 语言接口详解 核心概念 接口定义 在 Go 语言中&#xff0c;接口是一种抽象类型&#xff0c;它定义了一组方法的集合&#xff1a; // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的&#xff1a; // 矩形结构体…...

编程新知 2026/1/4 5:19:25

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序

一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

编程新知 2025/11/26 13:15:57

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测；从基础到高级，涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等

&#x1f50d; 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术&#xff0c;可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势&#xff0c;还能有效评价重大生态工程…...

编程新知 2025/9/12 15:10:44

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统

目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索&#xff08;基于物理空间 广播范围&#xff09;2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

编程新知 2025/12/12 6:01:17

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00

解读《网络安全法》最新修订，把握网络安全新趋势

《网络安全法》自2017年施行以来&#xff0c;在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂&#xff0c;网络攻击、数据泄露等事件频发&#xff0c;现行法律已难以完全适应新的风险挑战。 2025年3月28日&#xff0c;国家网信办会同相关部门起草了《网络安全…...

编程新知 2026/1/31 4:40:38

解决：Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist

现象&#xff1a; android studio报错&#xff1a; [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决&#xff1a; 不要动CMakeLists.…...

编程新知 2025/12/15 0:46:42

掌握 HTTP 请求：理解 cURL GET 语法

cURL 是一个强大的命令行工具&#xff0c;用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中&#xff0c;cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

编程新知 2025/7/9 20:52:19