前端算法面试之堆排序-每日一练
如果对前端八股文感兴趣,可以留意公重号:码农补给站,总有你要的干货。

今天分享一个非常热门的算法--堆排序。堆的运用非常的广泛,例如,Python中的heapq模块提供了堆排序算法,可以用于实现优先队列;Java中的PriorityQueue类实现了堆队列,可以用于实现优先级任务队列;C++中的优先队列容器适配器提供了基于堆的优先队列实现。
还有前端开发特别熟悉的React框架中也用到了,其中使用堆来管理组件的渲染优先级。在React中,组件的渲染优先级被抽象为一种堆结构,称为“Fiber堆”。Fiber堆中的每个节点代表一个组件,组件的优先级越高,在渲染时越优先。
什么是堆呢?
堆分为大根堆和小根堆,大根堆的每个结点的值都大于等于其子结点的值,即该结点是该子树中的最大值。小根堆的每个结点的值都小于等于其子结点的值,即该结点是该子树中的最小值。
他们都是一种特殊的完全二叉树,物理存储结构一般是一个连续的线性数组。并且节点的下标和左右子节点的下标之间存在一定的关系。假设节点的下标为 i,那么它的左子节点的下标为 2i,右子节点的下标为 2i + 1。相反地,如果一个节点的下标为 j,那么它的父节点的下标为 j/2(向下取整)。
那如何利用堆进行排序呢
以大根堆为例,就两步,建堆和堆化。
第一步先建堆,然后将堆顶和数组的最后一位更换位置,数组的最后一个位置就是最大值了。堆的大小减一。
第二步,再调整堆,使其再次满足大根堆的定义。
重复上面两步,直到堆的大小为1。
下面用代码实现这两个过程
建堆
class Heap {constructor(data) {this.data = data;}build() {for (let i = 2; i < this.data.length; i++) {this.heapfyTop(i);}}heapfyTop(n) {while (n > 1 && this.data[n] > this.data[Math.floor(n / 2)]) {this.swap(n, Math.floor(n / 2));n = Math.floor(n / 2);}}swap(index1, index2) {const temp = this.data[index1];this.data[index1] = this.data[index2];this.data[index2] = temp;}
}
建堆有两种方法,这里先讲第一种。
建堆的过程有点像插入排序,假设第一个元素已经是一个大根堆,从第二个节点开始往后遍历,每个元素都往前面的大根堆中插入。直到遍历完整个数组的元素。完整的大根堆就建好了。
假设往大根堆中插入元素a,先将元素a放到数组的最后一个位置,然后比较a元素和其父元素的大小,如果大于父元素,就将两个元素的位置更换。这样a元素就有了新的父元素。然后继续比较a 元素和其父元素的大小。直到a元素小于等于父元素,或者a元素变成了大根堆的堆顶。
这个比较的过程,就是大根堆堆化的过程
上面代码中,build函数作用是从数组的第二个元素开始往后遍历,每遍历一个元素,就调用一次heapfyTop 函数。heapfyTop 函数的作用是调整大根堆。遍历完整个数组,堆也就建好了。
数组元素从下标 1 开始
测试代码
const data = [-1, 21, 33, 5, 42, 123, 54, 65, 23, 33, 55];
const heap = new Heap(data);heap.build();console.log(heap.data);
// [
// -1, 123, 55, 65, 33,
// 42, 5, 54, 21, 23,
// 33
// ]
新建一个 Heap 类,然后调用 build 方法,并且将堆的内容打印出来。打印数组确实满足大根堆定义,没有问题。
堆排序
class Heap {//省略其他代码sort() {this.build2(); // 构建大顶堆let len = this.data.length - 1; // 数组长度减1,因为堆排序是从下标1开始while (len > 1) { // 当堆长度大于1时,继续排序this.swap(1, len); // 交换堆顶元素与堆尾元素len--; // 减小堆长度this.heapfyBelow(1, len); // 对新的堆顶元素进行调整}}heapfyBelow(n, end) { // 对下标为n的元素进行调整,使其满足大顶堆的性质,end为调整范围的上界// 是否是叶子节点while (n * 2 <= end) {let maxIndex = n; // 假设当前结点是最大值// 如果有左孩子,且左孩子的值比当前结点大,则将maxIndex更新为左孩子的下标if (n * 2 <= end && this.data[maxIndex] < this.data[n * 2]) maxIndex = n * 2;// 如果有右孩子,且右孩子的值比当前结点大,则将maxIndex更新为右孩子的下标if (n * 2 + 1 <= end && this.data[maxIndex] < this.data[n * 2 + 1]) maxIndex = n * 2 + 1;// 如果maxIndex没有发生变化,说明当前结点的值已经是最大值,调整结束if (maxIndex == n) break;// 否则,交换当前结点与maxIndex指向的结点this.swap(n, maxIndex);n = maxIndex; // 更新当前结点为新的maxIndex}}}
将堆顶元素和最后一个元素更换位置之后,堆的大小减一,并且需要重新调整堆的大小,所以代码中 len--,并且调用了this.heapfyBelow(1, len)。这也是一个堆调整的代码,与之前不同的是,这个代码是从上往下调整堆。不断地比较当前元素和子元素,如果有子元素比当前元素还大的,就更换位置。直到遍历到叶子节点,或者没有比当前元素更大的子节点。
为了方便调用者,sort 函数中直接调用了 build 函数,完成建堆的步骤。
测试代码
const data = [-1, 21, 33, 5, 42, 123, 54, 65, 23, 33, 55];
const heap = new Heap(data);
heap.sort();
console.log(heap.data);
// [
// -1, 5, 21, 23, 33,
// 33, 42, 54, 55, 65,
// 123
// ]
打印的数组有序,代码正确
完整代码
class Heap {constructor(data) {this.data = data;}build() {for (let i = 2; i < this.data.length; i++) {this.heapfyTop(i);}}sort() {this.build2();let len = this.data.length - 1;while (len > 1) {this.swap(1, len);len--;this.heapfyBelow(1, len);}}heapfyBelow(n, end) {// 是否是叶子节点while (n * 2 <= end) {let maxIndex = n;// 是否有左孩子if (n * 2 <= end && this.data[maxIndex] < this.data[n * 2]) maxIndex = n * 2;// 是否有右孩子if (n * 2 + 1 <= end && this.data[maxIndex] < this.data[n * 2 + 1]) maxIndex = n * 2 + 1;if (maxIndex == n) break;this.swap(n, maxIndex);n = maxIndex;}}heapfyTop(n) {while (n > 1 && this.data[n] > this.data[Math.floor(n / 2)]) {this.swap(n, Math.floor(n / 2));n = Math.floor(n / 2);}}swap(index1, index2) {const temp = this.data[index1];this.data[index1] = this.data[index2];this.data[index2] = temp;}
}const data = [-1, 21, 33, 5, 42, 123, 54, 65, 23, 33, 55];
const heap = new Heap(data);heap.sort();console.log(heap.data);
这是堆排序的完整代码,大家可以直接 copy 下来在本地跑一跑
总结
这篇文章分享了堆排序的概念讲解以及 JS 代码实现。堆排序是一种高效的排序算法,利用堆的特性进行排序。它的时间复杂度为O(nlogn),通过建堆和堆化的过程,可以将一个无序的数组转化为有序的数组。堆排序在实际应用中有广泛的应用,特别是在需要维护优先级队列的场景中非常有用。
下篇文章来分享建堆的另一种方式,以及堆的元素如何删除,并且分析堆排序的时间复杂度
作者:慢功夫
链接:https://juejin.cn/post/7300779513910132747
来源:稀土掘金
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
相关文章:

前端算法面试之堆排序-每日一练
如果对前端八股文感兴趣,可以留意公重号:码农补给站,总有你要的干货。 今天分享一个非常热门的算法--堆排序。堆的运用非常的广泛,例如,Python中的heapq模块提供了堆排序算法,可以用于实现优先队列…...
C++之set/multise容器
C之set/multise容器 set基本概念 set构造和赋值 #include <iostream> #include<set> using namespace std;void PrintfSet(set<int>&s) {for(set<int>::iterator it s.begin();it ! s.end();it){cout<<*it<<" ";}cout&l…...

本地部署AutoGPT
我们都了解ChatGPT,是Openai退出的基于GPT模型的新一代 AI助手,可以帮助解决我们在多个领域的问题。但是你会发现,在某些问题上,ChatGPT 需要经过不断的调教与沟通,才能得到接近正确的答案。对于你不太了解的领域领域&…...

ProtocolBuffers(protobuf)详解
目录 前言特点语法定义关键字JSON与Protocol Buffers互相转换gRPC与Protocol Buffers的关系 前言 Protocol Buffers(通常简称为protobuf)是Google公司开发的一种数据描述语言,它能够将结构化数据序列化,可用于数据存储、通信协议…...
HTTP 到 HTTPS 再到 HSTS 的转变
近些年,随着域名劫持、信息泄漏等网络安全事件的频繁发生,网站安全也变得越来越重要,也促成了网络传输协议从 HTTP 到 HTTPS 再到 HSTS 的转变。 HTTP HTTP(超文本传输协议) 是一种用于分布式、协作式和超媒体信息系…...
清华学霸告诉你:如何自学人工智能?
清华大学作为中国顶尖的学府之一,培养了许多优秀的人才,其中不乏在人工智能领域有所成就的学霸。通过一位清华学霸的经验分享,揭示如何自学人工智能,帮助你在这场科技浪潮中勇往直前。 一、夯实基础知识 数学基础:学习…...
Ubuntu 安装VMware Tools选项显示灰色,如何安装VMware Tools
切换apt源为阿里云: https://qq742971636.blog.csdn.net/article/details/134291339 只要你的网络没问题,你直接执行这几个命令,重启ubuntu虚拟机即可、 sudo dpkg --configure -a sudo apt-get autoremove open-vm-tools sudo apt-get ins…...

SpringBoot 2.x 实战仿B站高性能后端项目
SpringBoot 2.x 实战仿B站高性能后端项目 下栽の地止:请看文章末尾 通常SpringBoot新建项目,默认是集成了Maven,然后所有内容都在一个主模块中。 如果项目架构稍微复杂一点,就需要用到Maven多模块。 本文简单概述一下,…...
vscode文件夹折叠问题
今天发现一个vscode的文件夹显示的问题,首先是这样的,就是我的文件夹里又一个子文件夹,子文件夹里有一些文件,但是我发现无法折叠起这个子文件夹,总是显示全部的文件,这让我备份很难,具体参考 h…...
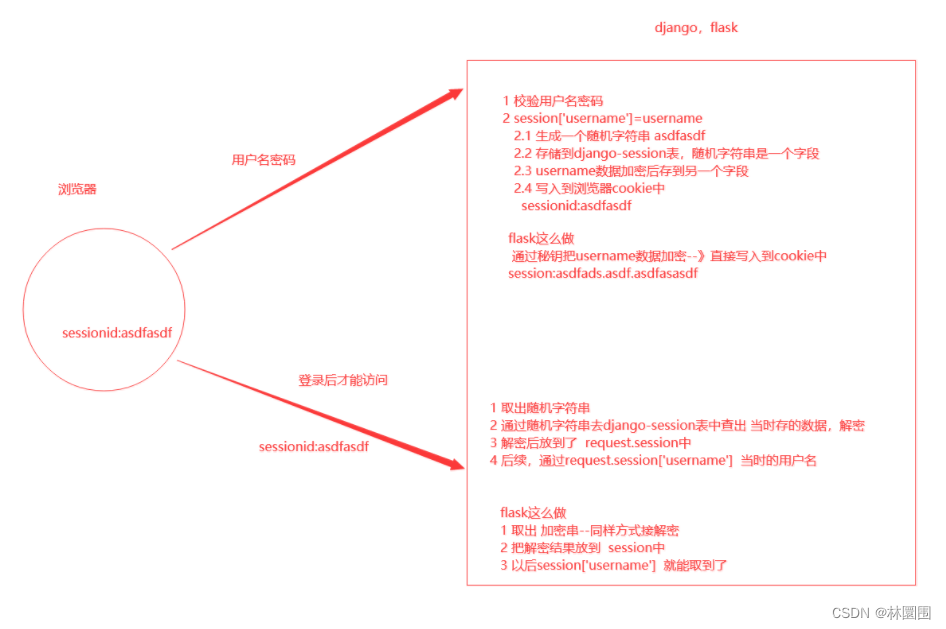
4-flask-cbv源码、Jinja2模板、请求响应、flask中的session、flask项目参考
1 flask中cbv源码 2 Jinja2模板 3 请求响应 4 flask中的session 5 flask项目参考 1 flask中cbv源码 ***flask的官网文档:***https://flask.palletsprojects.com/en/3.0.x/views/1 cbv源码执行流程1 请求来了,路由匹配成功---》执行ItemAPI.as_view(item…...
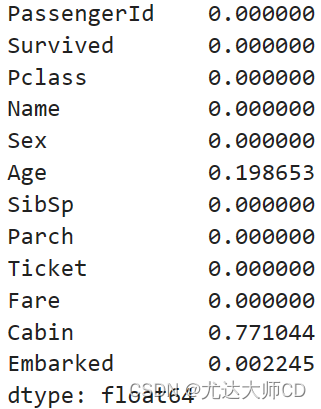
2.Pandas数据预处理
2.1 数据清洗 以titanic数据为例。 df pd.read_csv(titanic.csv) 2.1.1 缺失值 (1)缺失判断 df.isnull() (2)缺失统计 # 列缺失统计 df.isnull().sum(axis0) # 行缺失统计 df.isnull().sum(axis1) # 统计缺失率 df.isnu…...

C# IEnumerable<T>介绍
IEnumerable 是 C# 中的一个接口,它是 .NET Framework 中的集合类型的基础。任何实现了 IEnumerable 接口的对象都可以进行 foreach 迭代。 IEnumerable 只有一个方法,即 GetEnumerator,该方法返回一个 IEnumerator 对象。IEnumerator 对象用…...

九洲
《九洲》 作者/罗光记 九洲春色映朝阳, 洲渚风光似画廊。 柳絮飘飞花似雪, 九州繁华共锦裳。 水波荡漾鱼儿跃, 洲边鸟语唤晨光。 春风拂过千里岸, 九洲儿女笑语扬。...

基于Genio 700 (MT8390)芯片的AR智能眼镜方案
AR眼镜是一种具有前所未有发展机遇的设备,无论是显示效果、体积还是功能都有明显的提升。AR技术因其智能、实时、三维、多重交互和开放世界的特点备受关注。 AR眼镜集成了AR技术、语音识别、智能控制等多项高科技功能,可以帮助用户实现更加便捷、高效、个…...
锐捷OSPF认证
一、知识补充 1、基本概述 OSPF区域认证和端口认证是两种不同的认证机制,用于增强OSPF协议的安全性。 OSPF区域认证(OSPF Area Authentication):这种认证机制是基于区域的。在OSPF网络中,每个区域都可以配置一个区域…...

M2 Mac Xcode编译报错 ‘***.framework/‘ for architecture arm64
In /Users/fly/Project/Pods/YYKit/Vendor/WebP.framework/WebP(anim_decode.o), building for iOS Simulator, but linking in object file built for iOS, file /Users/fly/Project/Pods/YYKit/Vendor/WebP.framework/WebP for architecture arm64 这是我当时编译模拟器时报…...

Python算法题2023 输出123456789到98765432中完全不包含2023的数有多少
题目: 无输入,只需输出结果🤐 这个数字比较大,小伙伴们运行的时候要给代码一点耐心嗷つ﹏⊂ ,下面是思路,代码注释也很详细,大致看一下吧(^∀^●)…...
SpringBoot整合Thymeleaf
Thymeleaf 支持 HTML 原型,可以让前端工程师在浏览器中直接打开查看样式,也可以让后端工程师结合真实数据查看显示效果 Thymeleaf 除了展示基本的 HTML ,进行页面渲染之外,也可以作为一个 HTML 片段进行渲染,例如我们在…...

OpenAI的多函数调用(Multiple Function Calling)简介
我在六月份写了一篇关于GPT 函数调用(Function calling) 的博客https://blog.csdn.net/xindoo/article/details/131262670,其中介绍了函数调用的方法,但之前的函数调用,在一轮对话中只能调用一个函数。就在上周,OpenAI…...
在国内购买GPT服务前的一定要注意!!!
本人已经入坑GPT多日,从最开始的应用GPT到现在的自己研发GPT,聊聊我对使用ChatGPT的一些思考,有需要使用GPT的朋友或者正在使用GPT的朋友,一定要看完这篇文章,可能会比较露骨,也算是把国内知识库、AI的套路…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
