7.docker运行redis容器
1.准备redis的配置文件
从上一篇运行MySQL容器我们知道,需要给容器挂载数据卷,来持久化数据和配置,相应的redis也不例外。这里我们以redis6.0.8为例来实际说明下。
1.1 查找redis的配置文件redis.conf
下面这个网址有各种版本的配置文件供我们选择
https://redis.io/docs/management/config/
这里我们选择6.0的配置文件:由于篇幅问题,这里我就不再列出文件的具体内容了,可以自行查看。
https://raw.githubusercontent.com/redis/redis/6.0/redis.conf
1.2 修改配置文件redis.conf
- bind 注释掉,允许外部链接访问
- rotected-mode no ,不设置密码
- daemonize no 不允许守护运行(与docker -d 冲突)
1.3 确定容器数据卷的挂载目录
1.3.1 确定容器卷目录映射关系
将redis的数据卷挂载到宿主的以下目录:
- 配置文件
/data/redis/config/redis.conf:/etc/redis/redis.conf - 数据
/data/redis/data:/data
1.3.2 宿主机上修改好的redis.conf配置文件
2.运行redis容器
2.1 运行redis容器
docker run -p 6379:6379 --name myredis --privileged=true -v /data/redis/config/redis.conf:/etc/redis/redis.conf -v /data/redis/data:/data -d redis:6.0.8 redis-server /etc/redis/redis.conf

2.2 进入redis容器,验证使用
docker exec -it myredis /bin/bash
redis-cli
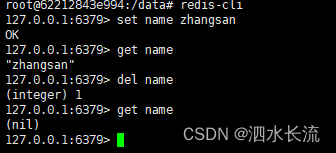
3.小结
到此为止,一个简单的单实例redis容器就启动成功了,是不是很简单啊。
注意,这里运行的redis容器仅供自己学习使用,不能用于生产,因为配置太简单,连最基本的哨兵模式都没有。
相关文章:

7.docker运行redis容器
1.准备redis的配置文件 从上一篇运行MySQL容器我们知道,需要给容器挂载数据卷,来持久化数据和配置,相应的redis也不例外。这里我们以redis6.0.8为例来实际说明下。 1.1 查找redis的配置文件redis.conf 下面这个网址有各种版本的配置文件供…...

unity教程
前言 伴随游戏行业的兴起,unity引擎的使用越来越普遍,本文章主要记录博主本人入门unity的相关记录大部分依赖siki学院进行整理。12 一、认识unity引擎? 1、Unity相关信息: Unity的诞生:https://www.jianshu.com/p/550…...

未定义与 ‘double‘ 类型的输入参数相对应的函数 ‘Link‘
报错 检查对函数"Link"得调用中是否缺失参数或参数数据类型不正确。 未定义与"double"类型的输入参数相对应的函数"Link"。 问题描述 网上搜了搜一般说是toolbox没有下载导致的,相当于调用的包本地没有。 但是我看看了 Robotics…...

为什么Transformer模型中使用Layer Normalization(Layer Norm)而不是Batch Normalization(BN)
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️ 👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
Vite - 配置 - 文件路径别名的配置
为什么要配置别名 别名的配置,主要作用是为了缩短代码中的导入路径。例如有如下的项目目录: project-name| -- src| -- a| --b| --c| --d| --e| -- abc.png| -- index.html| -- main.js如果想在 main.js 文件中使用 abc.png ,则使用的路径是 ࿱…...

phpStorm Xdebug调试 加FireFox浏览器
步骤1: [Xdebug] zend_extension“D:\phpstudy_pro\Extensions\php\php5.4.45nts\ext\php_xdebug.dll” xdebug.collect_params1 xdebug.collect_return1 xdebug.remote_enableOn xdebug.remote_hostlocalhost xdebug.remote_port9001 xdebug.remote_handlerdbgp ;…...

多维时序 | MATLAB实现PSO-BiGRU-Attention粒子群优化双向门控循环单元融合注意力机制的多变量时间序列预测
多维时序 | MATLAB实现PSO-BiGRU-Attention粒子群优化双向门控循环单元融合注意力机制的多变量时间序列预测 目录 多维时序 | MATLAB实现PSO-BiGRU-Attention粒子群优化双向门控循环单元融合注意力机制的多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 …...
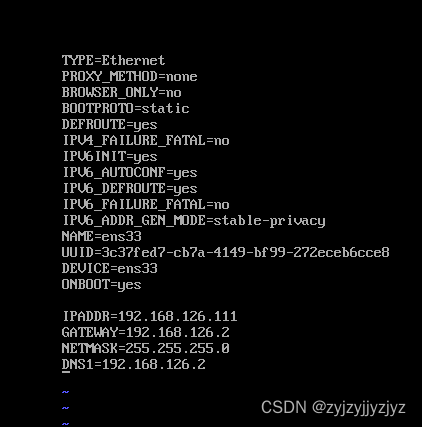
linux配置固定ip(两种方法)
首先刚下载的vm,刚创建的虚拟机,肯定是需要配置ip的 其次以前我的每次都是设置自动ip,这样每次登录都会自动获取ip地址,并且每次的ip都不相同。 ~方法: 开机登陆后 1)Cd /etc/sysconfig/network-scripts 2)Vi ifcf…...
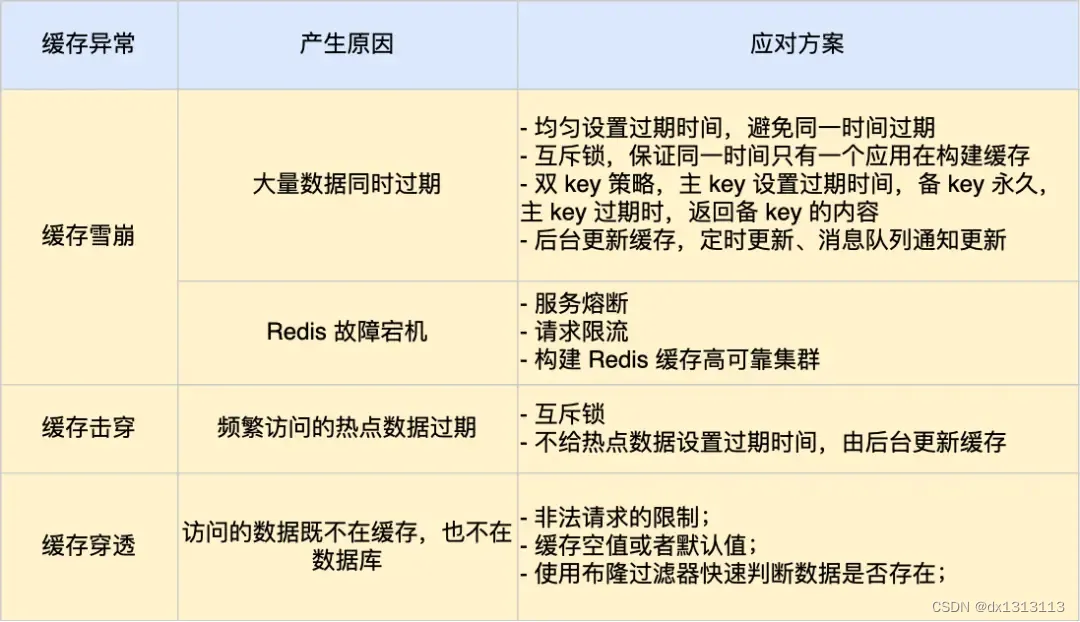
什么是缓存雪崩、击穿、穿透?
背景 数据一般是存储于数据库中,数据库中的数据都是存在磁盘上的,磁盘读写的速度相较于内存或者CPU中的寄存器来说是非常慢的了。 如果用户的请求都直接访问数据库的话,请求数量一上来,数据库很容易就崩溃了,所以为了…...

可以通过电脑远程控制安卓设备的软件
有些时候,我们需要用电脑远程控制安卓设备,比如远程维护门店设备、安卓系统的户外广告牌等等。我们来探索和比较几款允许用户通过电脑远程控制安卓设备的软件。 1、Splashtop Business Splashtop 是一种多功能远程访问解决方案,以其高性能流…...

HP惠普暗影精灵9笔记本电脑OMEN by HP Transcend 16英寸游戏本16-u0000原厂Windows11系统
惠普暗影9恢复出厂开箱状态,原装出厂Win11-22H2系统ISO镜像 下载链接:https://pan.baidu.com/s/17ftbBHEMFSEOw22tnYvPog?pwd91p1 提取码:91p1 适用型号:16-u0006TX、16-u0007TX、16-u0008TX、16-u0009TX、16-u0017TX 原厂系…...

vue2+elementUI 仿照SPC开发CPK分析工具
源码地址请访问 Vue CPK分析工具页面设计源码(支持左右可拖拽和表格可编辑、复制粘贴)仿照SPC开发-CSDN博客...
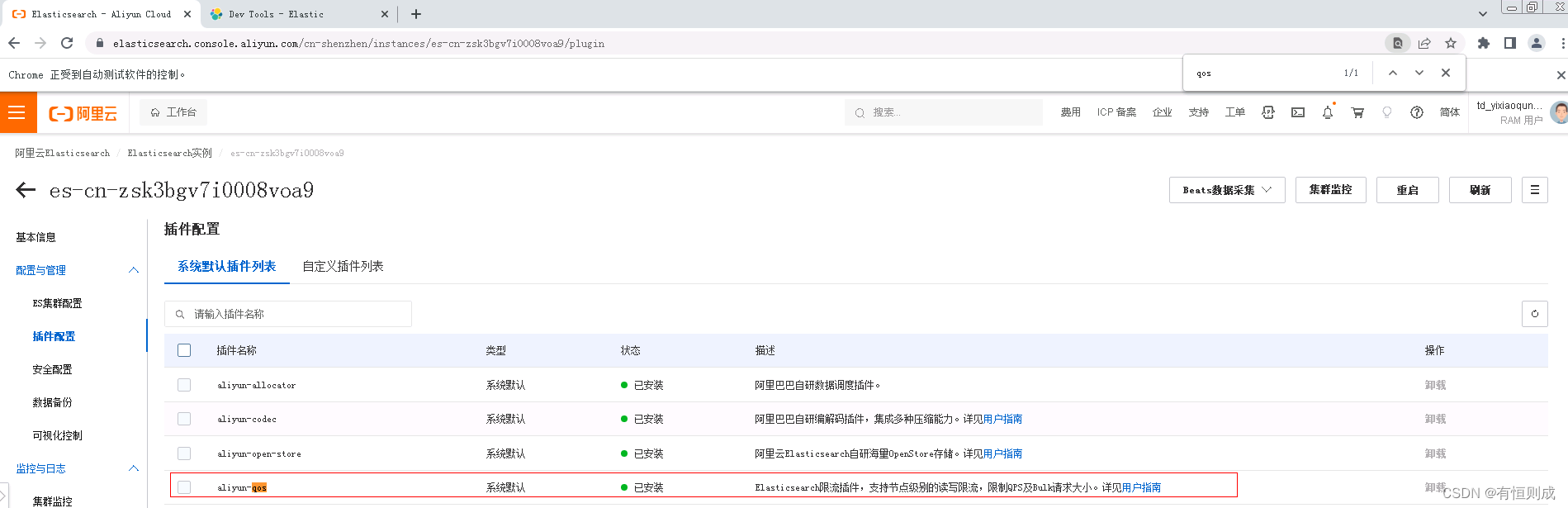
云ES使用集群限流插件(aliyun-qos)
aliyun-qos插件是阿里云Elasticsearch团队自研的插件,能够提高集群的稳定性。该插件能够实现集群级别的读写限流,在关键时刻对指定索引降级,将流量控制在合适范围内。例如当上游业务无法进行流量控制时,尤其对于读请求业务,可根据aliyun-qos插件设置的规则,按照业务的优先…...

2023.11.17 hadoop之HDFS进阶
目录 HDFS的机制 元数据简介 元数据存储流程:namenode 生成了多个edits文件和一个fsimage文件 edits和fsimage文件 SecondaryNameNode辅助NameNode的方式: HDFS的存储原理 写入数据原理: 发送写入请求,获取主节点同意,开始写入,写入完成 读取数据原理:发送读取请求,获取…...
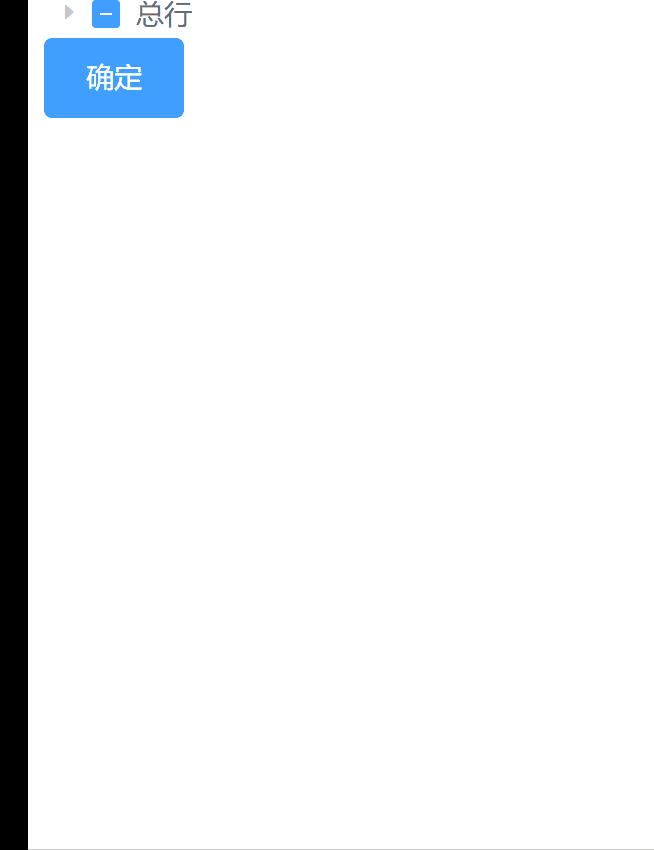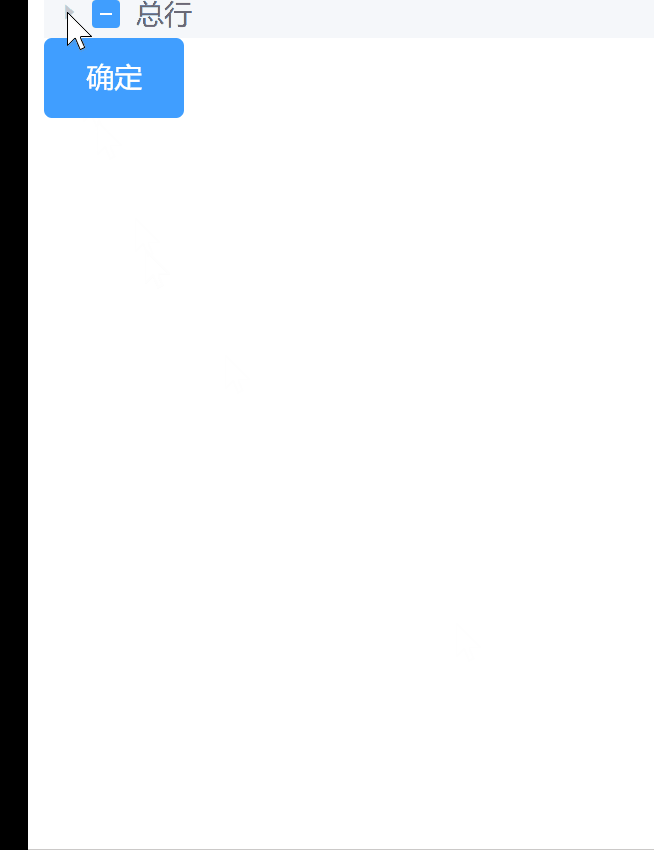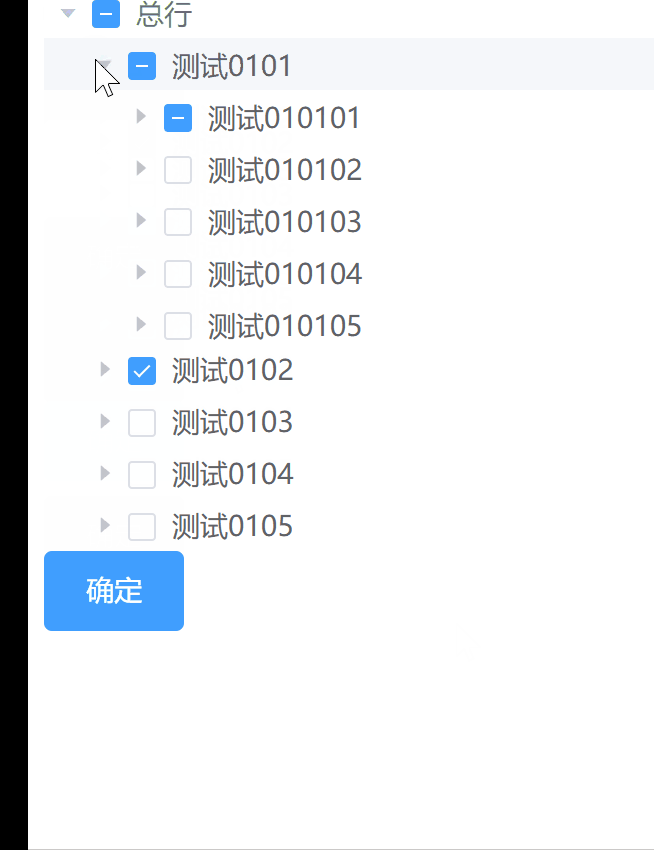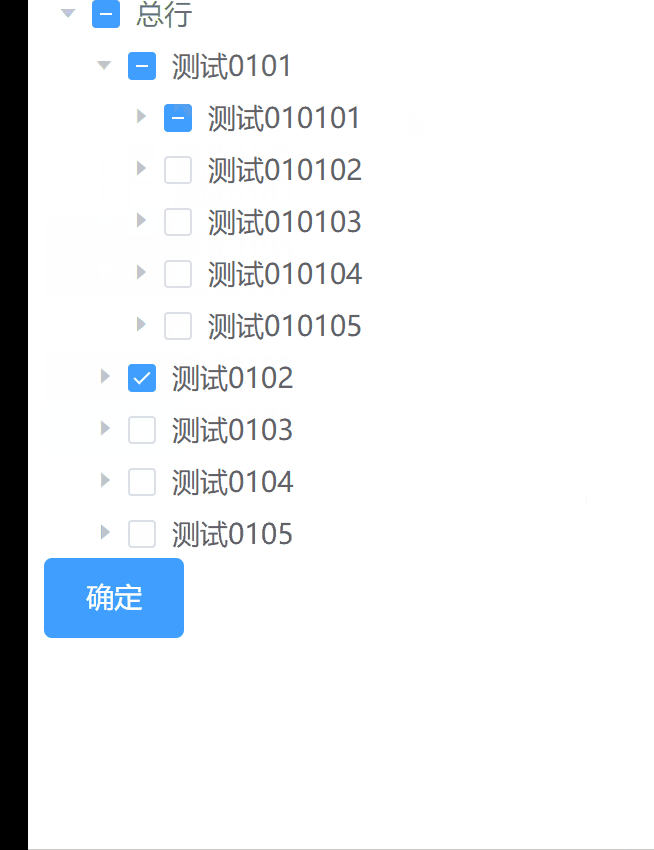
如何在el-tree懒加载并且包含下级的情况下进行数据回显-01
在项目中做需求,遇到一个比较棘手的问题,el-tree懒加载在包含下级的时候,需要做回显,将选中的数据再次勾选上,在处理这个需求的时候有两点是比较困难的: el-tree是懒加载的,包含下级需要一层一…...

系列六、JVM的内存结构【栈】
一、产生背景 由于跨平台性的设计,Java的指令都是根据栈来设计的,不同平台的CPU架构不同,所以不能设计为基于寄存器的。 二、概述 栈也叫栈内存,主管Java程序的运行,是在线程创建时创建,线程销毁时销毁&…...
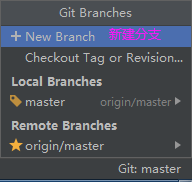
技巧篇:在Pycharm中配置集成Git
一、在Pycharm中配置集成Git 我们使用git需要先安装git工具,这里给出下载地址,下载后一路直接安装即可: https://git-for-windows.github.io/ 0. git中的一些常用词释义 Repository name: 仓库名称 Description(可选):…...
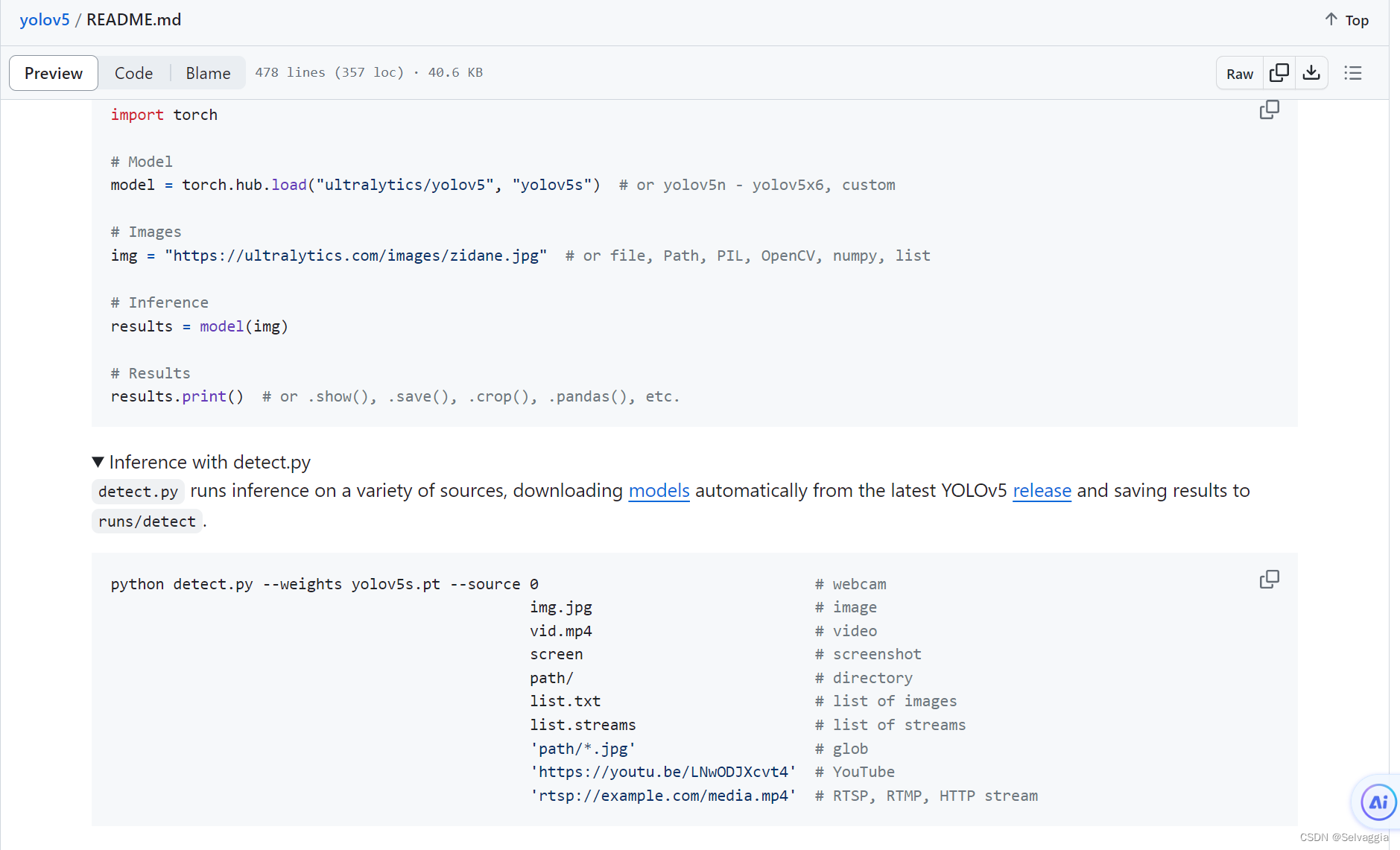
Yolov5
Yolov5 Anchor 1.Anchor是啥? anchor字面意思是锚,是个把船固定的东东(上图),anchor在计算机视觉中有锚点或锚框,目标检测中常出现的anchor box是锚框,表示固定的参考框…...
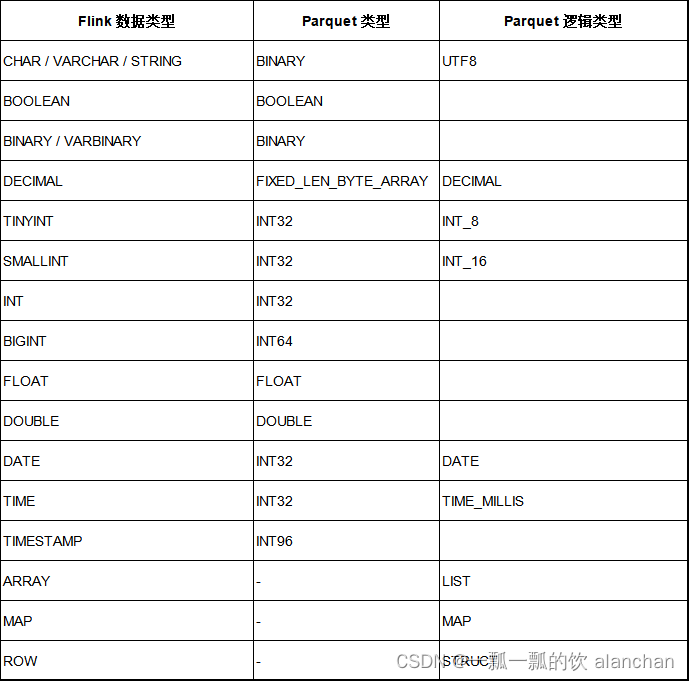
36、Flink 的 Formats 之Parquet 和 Orc Format
Flink 系列文章 1、Flink 部署、概念介绍、source、transformation、sink使用示例、四大基石介绍和示例等系列综合文章链接 13、Flink 的table api与sql的基本概念、通用api介绍及入门示例 14、Flink 的table api与sql之数据类型: 内置数据类型以及它们的属性 15、Flink 的ta…...
--安装)
Docker 笔记(一)--安装
Docker 笔记(一)–安装 记录Docker 安装操作记录,便于查询。 参考 链接: Docker 入门到实战教程(二)安装Docker链接: docker入门(利用docker部署web应用)链接: 阿里云容器镜像服务/镜像加速器/操作文档链接: 网易镜像中心链接: 阿里云镜像…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
