Apriori算法
Apriori算法由R. Agrawal和R. Srikant于1994年在数据集中寻找布尔关联规则的频繁项集。该算法的名称是Apriori,因为它使用了频繁项集属性的先验知识。我们应用迭代方法或逐层搜索,其中k-频繁项集用于找到k+1个项集。
为了提高频繁项集逐层生成的效率,使用了一个重要的属性Apriori属性,该属性有助于减少搜索空间。
Apriori属性
频繁项集的所有非空子集必须是频繁项集。Apriori算法的核心概念是支持度的反单调性。Apriori假设,
频繁项集的所有子集必须是频繁的(Apriori属性)。
如果一个项集是不频繁的,那么它的所有超集都是不频繁的。
在我们开始理解算法之前,可以看看前一篇文章中解释过的一些定义。
考虑以下数据集,我们将找到频繁项集并为其生成关联规则。
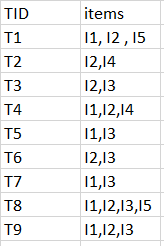
最小支持计数为2
最低置信度为60%
步骤1:K=1
(I)创建一个表,其中包含数据集中存在的每个项目的支持计数-称为C1(候选集)
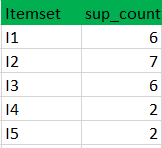
(II)将候选集合项的支持计数与最小支持计数进行比较(这里min_support=2,如果候选集合项的support_count小于min_support,则移除那些项)。这给了我们项集L1。
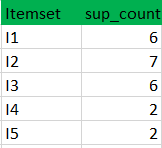
步骤2:K=2
- 使用L1生成候选集C2(这称为连接步骤)。连接Lk-1和Lk-1的条件是它应该具有共同的(K-2)个元素。
- 检查项目集的所有子集是否频繁,如果不频繁,则删除该项目集。({I1,I2}的示例子集是{I1},{I2},它们是频繁的。检查每个项集)
- 现在通过在dataset中搜索来找到这些项集的支持计数。
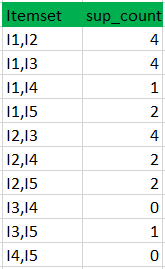
将候选(C2)支持计数与最小支持计数进行比较(这里min_support=2,如果候选集合项的support_count小于min_support,则移除那些项),这给出了项集合L2。
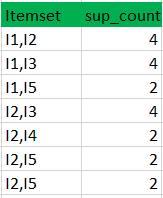
步骤3:
-
使用L2生成候选集合C3(连接步骤)。连接Lk-1和Lk-1的条件是它应该具有共同的(K-2)个元素。所以这里,对于L2,第一个元素应该匹配。
所以通过连接L2生成的项集是{I1,I2,I3}{I1,I2,I5}{I1,I3,I5}{I2,I3,I4}{I2,I4,I5}{I2,I3,I5} -
检查这些项集的所有子集是否都是频繁的,如果不是,则删除该项集。({I1,I2,I3}的子集是{I1,I2},{I2,I3},{I1,I3},它们是频繁的。对于{I2,I3,I4},子集{I3,I4}不是频繁的,因此将其移除。类似地检查每个项集)
-
通过在数据集中搜索来找到这些剩余项集的支持计数。
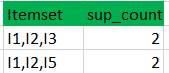
将候选(C3)支持计数与最小支持计数进行比较(这里min_support=2,如果候选集合项的support_count小于min_support,则移除那些项),这给出了项集合L3。
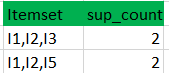
步骤4:
- 使用L3生成候选集合C4(连接步骤)。连接Lk-1和Lk-1(K=4)的条件是,它们应该具有(K-2)个共同元素。因此,对于L3,前两个元素(项目)应该匹配。
- 检查这些项集的所有子集是否频繁(这里通过连接L3形成的项集是{I1,I2,I3,I5},因此其子集包含{I1,I3,I5},这不是频繁的)。所以C4中没有项集
- 我们停在这里,因为没有进一步发现频繁项集
这样,我们就发现了所有的频繁项集。强关联规则的生成是目前研究的热点。为此,我们需要计算每个规则的置信度。
置信度
60%的置信度意味着60%的购买牛奶和面包的顾客也购买了黄油。
Confidence(A->B)=Support_count(A∪B)/Support_count(A)
因此,在这里,通过以任何频繁项集为例,我们将展示规则生成。
Itemset {I1, I2, I3} //from L3
SO rules can be
[I1^I2]=>[I3] //confidence = sup(I1^I2^I3)/sup(I1^I2) = 2/4*100=50%
[I1^I3]=>[I2] //confidence = sup(I1^I2^I3)/sup(I1^I3) = 2/4*100=50%
[I2^I3]=>[I1] //confidence = sup(I1^I2^I3)/sup(I2^I3) = 2/4*100=50%
[I1]=>[I2^I3] //confidence = sup(I1^I2^I3)/sup(I1) = 2/6*100=33%
[I2]=>[I1^I3] //confidence = sup(I1^I2^I3)/sup(I2) = 2/7*100=28%
[I3]=>[I1^I2] //confidence = sup(I1^I2^I3)/sup(I3) = 2/6*100=33%
因此,如果最小置信度为50%,则前3条规则可以被认为是强关联规则。
Apriori算法的局限性
Apriori算法可能很慢。主要的限制是需要时间来保持大量的候选集,具有非常频繁的项集,低的最小支持度或大的项集,即它不是一个有效的方法,用于大量的数据集。
例如,如果有104个来自频繁1-项集,则需要生成超过107个候选项到2-长度中,然后这些候选项将被测试和累积。此外,为了检测大小为100的频繁模式,即v1,v2… v100,必须生成2^100个候选项集,这导致候选项集生成的成本和时间浪费。因此,它将从候选项集中检查许多集合,并且它将多次重复地扫描数据库以寻找候选项集。当存储器容量有限且事务数量较多时,Apriori将非常低且效率低下。
[来源:https://arxiv.org/pdf/1403.3948.pdf]
相关文章:

Apriori算法
Apriori算法由R. Agrawal和R. Srikant于1994年在数据集中寻找布尔关联规则的频繁项集。该算法的名称是Apriori,因为它使用了频繁项集属性的先验知识。我们应用迭代方法或逐层搜索,其中k-频繁项集用于找到k1个项集。 为了提高频繁项集逐层生成的效率&…...

肖sir__linux讲解(2.1)
linux命令 cp 复制命令 a、cp 原文件名称 新文 件名称(不存在的文件) 案例:cp a k 截图: b.cp 原文件名称 原有文 件名称(存在的文件) 案例:cp a b 截图: c、cp 指定路径复制 格式ÿ…...

The ultimate UI kit and design system for Figma 组件库下载
Untitled UI 是世界上最大的 Figma UI 套件和设计系统。可以启动任何项目,为您节省数千小时,并祝您升级为专业设计师。 采用 100% 自动布局 5.0、变量、智能变体和 WCAG 可访问性精心制作。 900全局样式、变量:超级智能的全局颜色、排版和效…...

Selenium——利用input标签上传文件
Selenium利用input标签上传文件 完整流程 打开文件上传页面选择要上传的文件点击上传按钮确认文件上传成功介绍怎么方便的获取对应元素的Xpath或者Css 简单介绍 在使用Selenium进行浏览器自动化测试时,文件上传是一个常见的需求。而 标签就是实现文件上传功能的…...
C++初阶 日期类的实现(下)
目录 一、输入输出(>>,<<)重载的实现 1.1初始版 1.2友元并修改 1.2.1简单介绍下友元 1.2.2修改 1.3>>重载 二、条件判断操作符的实现 2.1操作符的实现 2.2!操作符的实现 2.3>操作符的实现 2.4>,<,<操作符的实现 三、日期-日期的实现 …...

大师学SwiftUI第16章 - UIKit框架集成
其它相关内容请见虚拟现实(VR)/增强现实(AR)&visionOS开发学习笔记 SwiftUI是一套新框架,因此并没有包含我们构建专业应用所需的所有工具。这意味着我们会需要求助于UIKit(移动设备)和AppKit(Mac电脑)等原…...
7.docker运行redis容器
1.准备redis的配置文件 从上一篇运行MySQL容器我们知道,需要给容器挂载数据卷,来持久化数据和配置,相应的redis也不例外。这里我们以redis6.0.8为例来实际说明下。 1.1 查找redis的配置文件redis.conf 下面这个网址有各种版本的配置文件供…...

unity教程
前言 伴随游戏行业的兴起,unity引擎的使用越来越普遍,本文章主要记录博主本人入门unity的相关记录大部分依赖siki学院进行整理。12 一、认识unity引擎? 1、Unity相关信息: Unity的诞生:https://www.jianshu.com/p/550…...

未定义与 ‘double‘ 类型的输入参数相对应的函数 ‘Link‘
报错 检查对函数"Link"得调用中是否缺失参数或参数数据类型不正确。 未定义与"double"类型的输入参数相对应的函数"Link"。 问题描述 网上搜了搜一般说是toolbox没有下载导致的,相当于调用的包本地没有。 但是我看看了 Robotics…...

为什么Transformer模型中使用Layer Normalization(Layer Norm)而不是Batch Normalization(BN)
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️ 👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
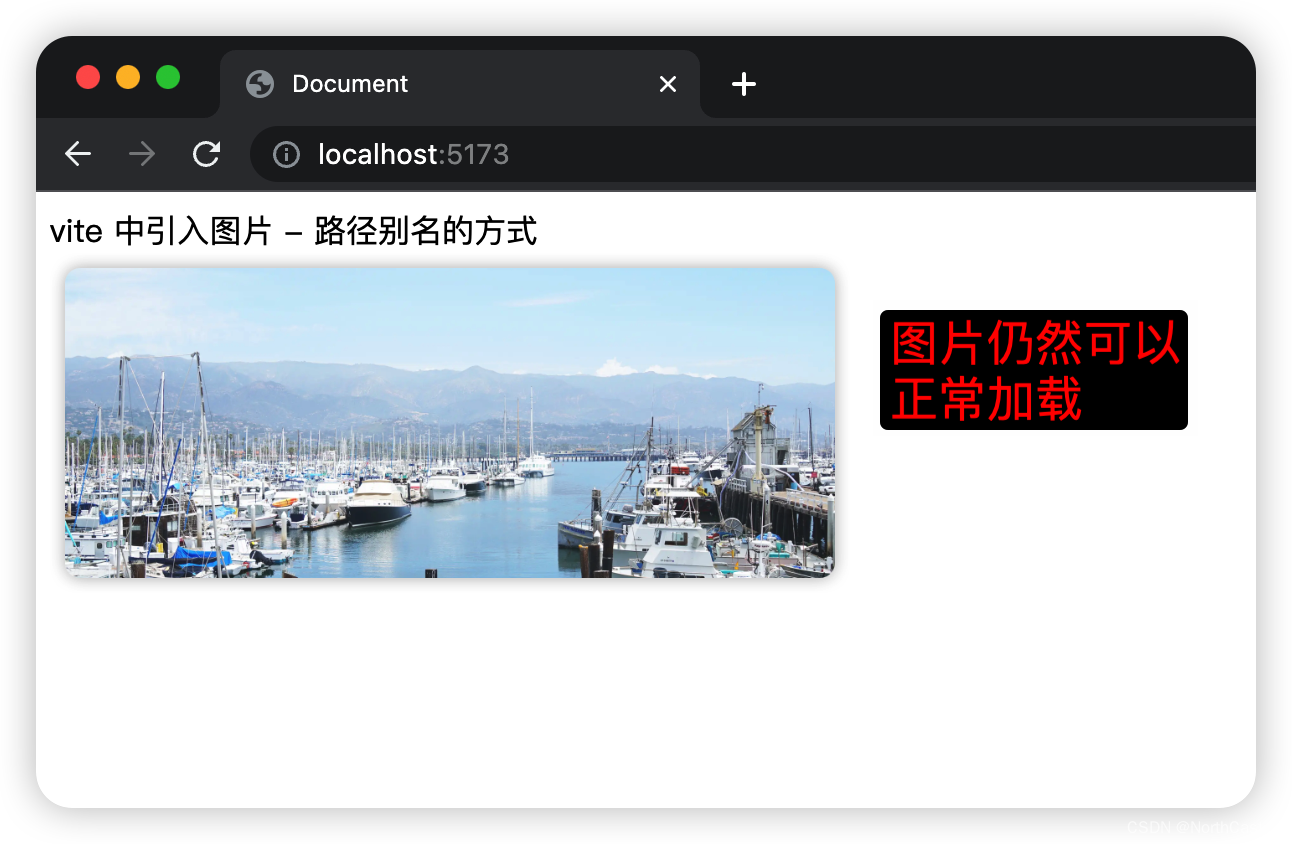
Vite - 配置 - 文件路径别名的配置
为什么要配置别名 别名的配置,主要作用是为了缩短代码中的导入路径。例如有如下的项目目录: project-name| -- src| -- a| --b| --c| --d| --e| -- abc.png| -- index.html| -- main.js如果想在 main.js 文件中使用 abc.png ,则使用的路径是 ࿱…...

phpStorm Xdebug调试 加FireFox浏览器
步骤1: [Xdebug] zend_extension“D:\phpstudy_pro\Extensions\php\php5.4.45nts\ext\php_xdebug.dll” xdebug.collect_params1 xdebug.collect_return1 xdebug.remote_enableOn xdebug.remote_hostlocalhost xdebug.remote_port9001 xdebug.remote_handlerdbgp ;…...

多维时序 | MATLAB实现PSO-BiGRU-Attention粒子群优化双向门控循环单元融合注意力机制的多变量时间序列预测
多维时序 | MATLAB实现PSO-BiGRU-Attention粒子群优化双向门控循环单元融合注意力机制的多变量时间序列预测 目录 多维时序 | MATLAB实现PSO-BiGRU-Attention粒子群优化双向门控循环单元融合注意力机制的多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 …...
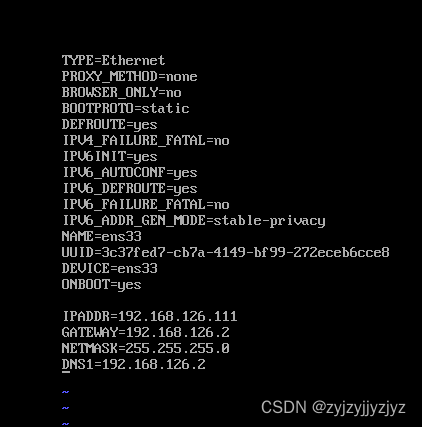
linux配置固定ip(两种方法)
首先刚下载的vm,刚创建的虚拟机,肯定是需要配置ip的 其次以前我的每次都是设置自动ip,这样每次登录都会自动获取ip地址,并且每次的ip都不相同。 ~方法: 开机登陆后 1)Cd /etc/sysconfig/network-scripts 2)Vi ifcf…...
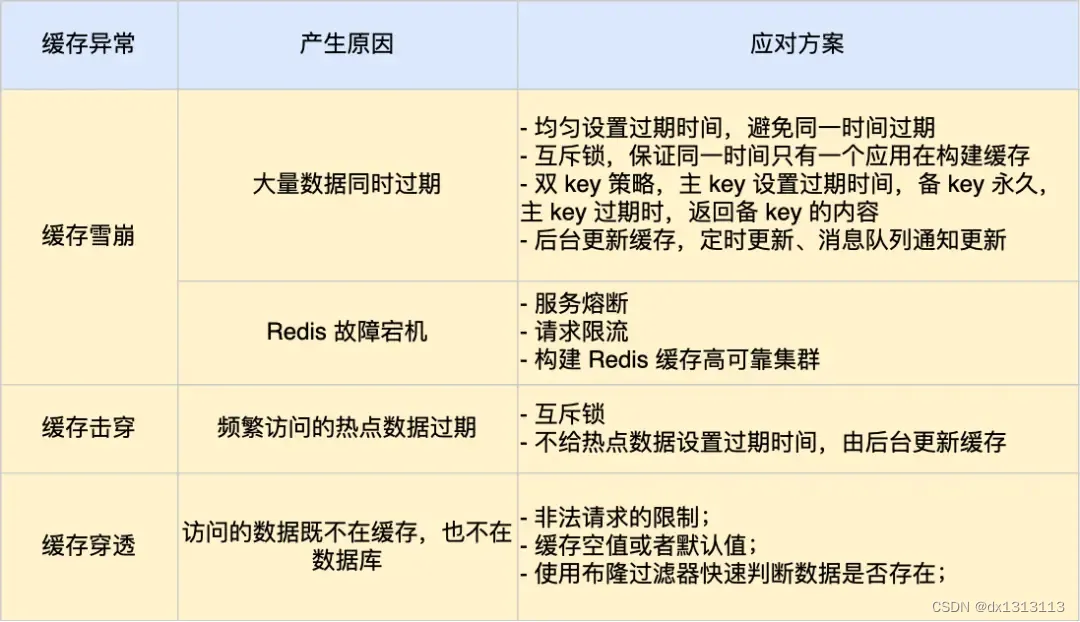
什么是缓存雪崩、击穿、穿透?
背景 数据一般是存储于数据库中,数据库中的数据都是存在磁盘上的,磁盘读写的速度相较于内存或者CPU中的寄存器来说是非常慢的了。 如果用户的请求都直接访问数据库的话,请求数量一上来,数据库很容易就崩溃了,所以为了…...

可以通过电脑远程控制安卓设备的软件
有些时候,我们需要用电脑远程控制安卓设备,比如远程维护门店设备、安卓系统的户外广告牌等等。我们来探索和比较几款允许用户通过电脑远程控制安卓设备的软件。 1、Splashtop Business Splashtop 是一种多功能远程访问解决方案,以其高性能流…...

HP惠普暗影精灵9笔记本电脑OMEN by HP Transcend 16英寸游戏本16-u0000原厂Windows11系统
惠普暗影9恢复出厂开箱状态,原装出厂Win11-22H2系统ISO镜像 下载链接:https://pan.baidu.com/s/17ftbBHEMFSEOw22tnYvPog?pwd91p1 提取码:91p1 适用型号:16-u0006TX、16-u0007TX、16-u0008TX、16-u0009TX、16-u0017TX 原厂系…...

vue2+elementUI 仿照SPC开发CPK分析工具
源码地址请访问 Vue CPK分析工具页面设计源码(支持左右可拖拽和表格可编辑、复制粘贴)仿照SPC开发-CSDN博客...
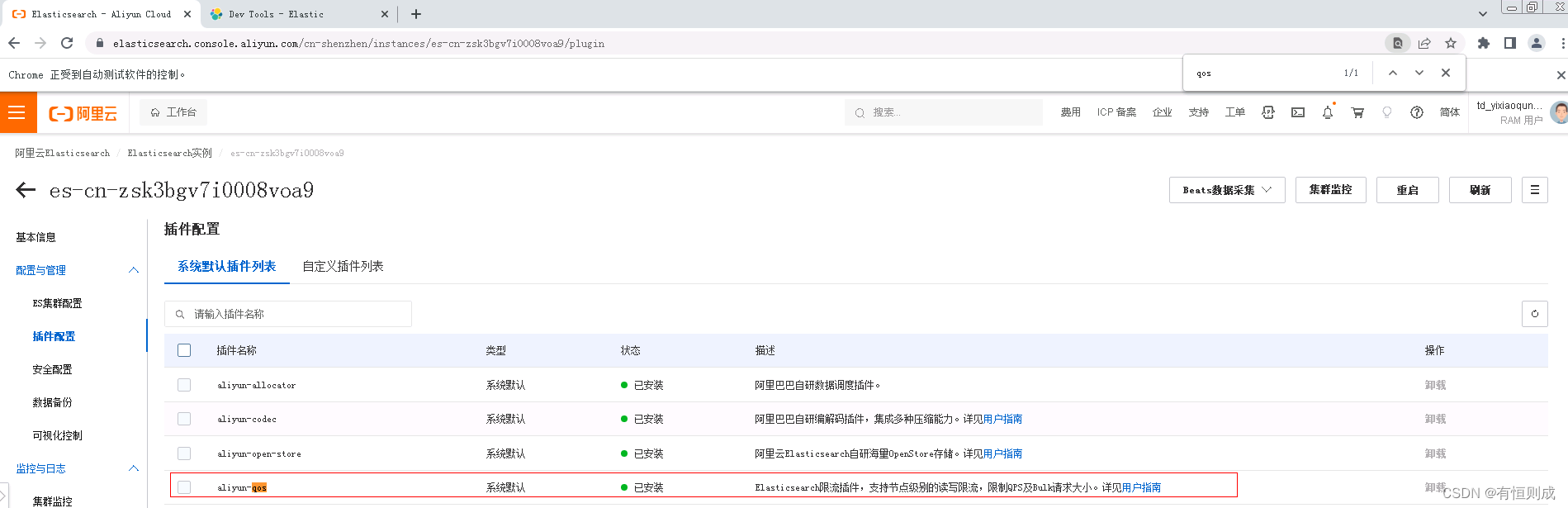
云ES使用集群限流插件(aliyun-qos)
aliyun-qos插件是阿里云Elasticsearch团队自研的插件,能够提高集群的稳定性。该插件能够实现集群级别的读写限流,在关键时刻对指定索引降级,将流量控制在合适范围内。例如当上游业务无法进行流量控制时,尤其对于读请求业务,可根据aliyun-qos插件设置的规则,按照业务的优先…...

2023.11.17 hadoop之HDFS进阶
目录 HDFS的机制 元数据简介 元数据存储流程:namenode 生成了多个edits文件和一个fsimage文件 edits和fsimage文件 SecondaryNameNode辅助NameNode的方式: HDFS的存储原理 写入数据原理: 发送写入请求,获取主节点同意,开始写入,写入完成 读取数据原理:发送读取请求,获取…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
