元宇宙3D云展厅应用到汽车销售的方案及特点
为了紧紧抓住年轻消费者的需求,汽车销售行业也正在经历一场深刻的变革。在这个变革的前沿,元宇宙3D汽车展厅作为一项全新技术闪亮登场,打破了传统汽车销售模式的限制,为消费者带来了前所未有的购车体验。
元宇宙3D汽车展厅采用了尖端的web3D开发建模和VR虚拟现实制作技术,将真实汽车展厅完整地呈现在虚拟世界中。消费者可以通过智能设备,在任何时间、任何地点参观这个虚拟展厅,感受其中的每一款车型的细腻之处。这种沉浸式的购车体验,让消费者能够更加直观地了解汽车的外观、内饰、配置等各个方面,为购车决策提供更全面的参考。
与传统的汽车销售模式相比,元宇宙3D汽车展厅极大地扩展了汽车销售的渠道和覆盖范围,不再受限于实体展厅的地理位置和开放时间。其次,通过web3D建模技术,消费者可以以更自由、更细致的方式探索车型,比如打开车门,进入车内驾驶区,实时变换不同演策款式,甚至还能提供线上试驾,无形中让产品更加形象地“介绍”给用户,充分拉近品牌与消费者内心之间的距离。
进入虚拟展厅后,用户可以开展自由探索,就如同进入线下门店一般,涵盖各系车型、实操指南等,全方位了解比亚迪品牌及其新能源车型。消费者还可以在展厅内体验定制化互动,通过虚拟平台了解产品细节和参数配置,其中也配备AI虚拟顾问,提供个性化解决方案。

元宇宙作为汽车线上虚拟营销空间,可提供沉漫式、互动式客户体验,助力消费者在虚拟环境中定制汽车。此外,它也可降低实体展厅成本,拓宽客户群体,提升客户满意度,推动汽车行业转型升级和在线销售业务发展。
元宇宙展厅可以设置互动游戏环节,提高观众的体验和参与度。例如,一些汽车企业可以设置赛车游戏环节,让观众在游戏中了解汽车性能和驾驶感受。这种互动游戏环节,可以提高品牌认知度和客户黏性,增强品牌形象和市场竞争力。
元宇宙展厅可以利用人工智能技术,提供个性化和差异化的服务,提高用户体验。例如,一些化妆品企业可以通过人脸识别技术,分析用户的肤质和需求,为用户提供定制化的化妆品建议。这种个性化和差异化的服务,可以提高用户满意度和忠诚度,增强品牌口碑和市场竞争力。
总之,元宇宙3D汽车展厅作为汽车企业的一次新尝试,更多的是一种对新兴营销方式的探索,区别于现实世界中的所见所闻,元宇宙给予了大众一种亦真亦幻的体验感,侧面激活了消费者的好奇心。为汽车销售行业注入新的活力。
相关文章:

元宇宙3D云展厅应用到汽车销售的方案及特点
为了紧紧抓住年轻消费者的需求,汽车销售行业也正在经历一场深刻的变革。在这个变革的前沿,元宇宙3D汽车展厅作为一项全新技术闪亮登场,打破了传统汽车销售模式的限制,为消费者带来了前所未有的购车体验。 元宇宙3D汽车展厅采用了尖…...
SourceTree修改Git密码
SourceTree用的好好的,无奈公司隔段时间强制更改电脑密码。更改完成后SourceTree无法使用,重新输入密码。VS的nuget也是。查资料虽然也能比较快的解决,但是。。。。在此转载记录下。 1. 找到 SourceTree 配置文件所在目录 ‘userhosts’ 目录…...

java中的深度复制和浅复制的BUG
刷题刷到LeetCode回溯DFS的算法题39题的时候,碰见一个Arraylist里面的bug,其中dfs函数里面的第一个if判断里面的语句 paths.add(path); path.clear();其中path是添加了path,但是添加之后path.clear(),导致原来添加到paths的path置为空数组,因为ArrayList的add只是把一个引用指…...

计算机毕业设计 基于SpringBoot的车辆网位置信息管理系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...

集软件库、论坛、社区、工具箱、积分商城、会员体系、在线商城一体的后台系统+HBuilderX 前端软件社区
集软件库、论坛、社区、工具箱、积分商城、会员体系、在线商城等多个功能于一体的全面后台系统加上强大的HBuilderX前端软件社区,为用户提供了全面的应用开发和交流平台 企业猫提供了完善的后台搭建服务,通过该服务,用户可以方便地搭建出所需…...
】)
【解决Qt编译报错:-1: warning: **.so, not found(try using -rpath or -rpath-link)】
[TOC](Qt调用opencv报错👎 warning: libopencv_flann.so.406, needed by **//libopencv_features2d.so, not found (try using -rpath or -rpath-link)) 最终提示使用-rpath,于是抱着试试看的方法改写.pro文件: QMAKE_LIBDIR_FLAGS -Wl,-r…...

关于数据mysql ->maxwell->kafka的数据传输
个人名片: 🐅作者简介:一名大三在校生,热爱生活,爱好敲码! \ 💅个人主页 🥇:holy-wangle ➡系列内容: 🖼️ tkinter前端窗口界面创建与优化 &…...

【linux】查看CPU的使用率
命令1:top top 总体系统信息 uptime:系统的运行时间和平均负载。tasks:当前运行的进程和线程数目。CPU:总体 CPU 使用率和各个核心的使用情况。内存(Memory):总体内存使用情况、可用内存和缓存…...
)
【系统稳定性】1.6 黑屏(三)
五,QNX启动异常 qnx启动异常无疑同样是灾难级的存在。qnx是目前座舱方案中主流的存在,如果qnx存在异常会导致host或la或其他娱乐世界offline。那么导致qnx的原因有很多,相应地,我们也有很多的排查手段。 5.1 以太网连接 座舱方案中目前还是多域的设计,那么多域之间的连…...
《使用EasyExcel在Excel中增加序号列的方法》
《使用EasyExcel在Excel中增加序号列的方法》 1、简介2、正文3、核心代码4、使用方法5、效果 1、简介 在处理Excel文件时,有时候需要为表格增加序号列。本文介绍了如何使用Java代码实现在Excel中增加序号列的功能,并提供了一个示例代码。 2、正文 在处理…...

【Linux】安全审计-audit
文章目录 一、audit简介二、开启auditd服务三、相关文件四、审计规则五、审计日志查询及分析附录1:auditctl -h附录2:systemcall 类型 参考文章: 1、安全-linux audit审计使用入门 2、audit详细使用配置 3、Linux-有哪些常见的System Call&a…...

Linux 之查看标准错误码工具
目录 1. Linux 之查看标准错误码工具 1. Linux 之查看标准错误码工具 $ sudo apt install moreutils$ errno -l EPERM 1 不允许的操作 ENOENT 2 没有那个文件或目录 ESRCH 3 没有那个进程 EINTR 4 被中断的系统调用 EIO 5 输入/输出错误 ENXIO 6 没有那个设备或地址 E2BIG 7 参…...

Git企业开发级讲解(五)
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、bug 分⽀二、删除临时分支三、小结 一、bug 分⽀ 假如我们现在正在 dev2 分⽀上进⾏开发…...

目录自动清洗
文章目录 前言一、需求分析二、操作步骤详解(标准章节)1. 提取文章目录2. 更改保存目录.txt3. 二级标题前面加4个空格4. 在章字和节字后面添加一个空格5. 在页码前面加上>符号6. 代码完全体 三、进阶一(有章无节小数二级标题)1…...

c++实现Any类,让一个类型指向其他任意类型
在c中,对于以上任务,容易想到的是一个基类类型指向其所有派生类。因此设计一个Any类,其里面有一个成员基类Base类,其派生类可以是数据date,但是你不知道date到底是什么东西,所以需要使用模版。所以其结构为…...
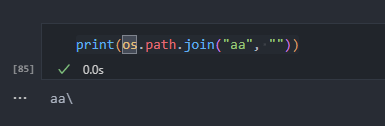
os.path.join函数用法
os.path.join()是Python中用于拼接文件路径的函数,它可以将多个字符串拼接成一个路径,并且会根据操作系统的规则自动使用合适的路径分隔符。 注:Linux用的是/分隔符,而Windows才用的是\。 该函数属于os.path模块,因此在…...

vscode Prettier配置
常用配置项: .prettierrc.json 是 Prettier 格式化工具的配置文件 {"printWidth": 200, // 指定行的最大长度"tabWidth": 2, // 指定缩进的空格数"useTabs": false, // 是否使用制表符进行缩进,默认为 false"singl…...
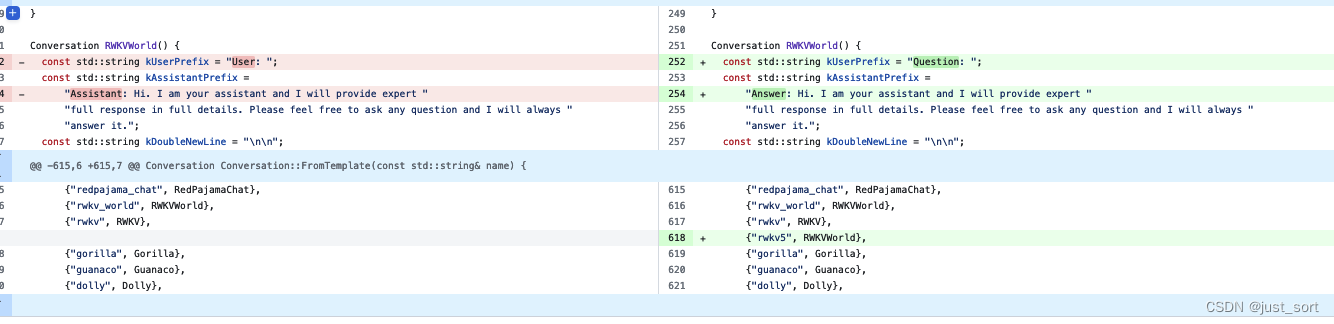
MLC-LLM 支持RWKV-5推理以及对RWKV-5的一些思考
自从2023年3月左右,chatgpt火热起来之后,我把关注的一些知乎帖子都记录到了这个markdown里面,:https://github.com/BBuf/how-to-optim-algorithm-in-cuda/tree/master/large-language-model-note ,从2023年3月左右到现…...
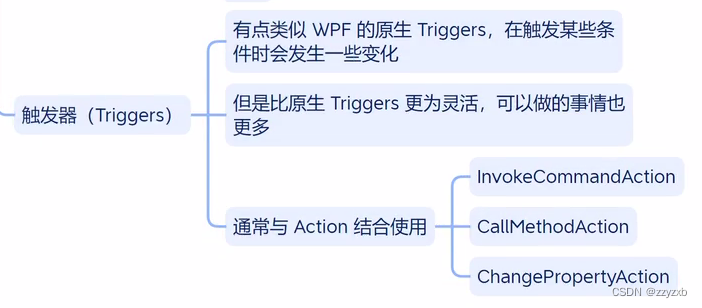
WPF中行为与触发器的概念及用法
完全来源于十月的寒流,感谢大佬讲解 一、行为 (Behaviors) behaviors的简单测试 <Window x:Class"Test_05.MainWindow"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winf…...

2023-2024华为ICT大赛-计算赛道-广东省省赛初赛-高职组-部分赛题分析【2023.11.18】
2023-2024华为ICT大赛 计算赛道 广东省 省赛 初赛 高职组 部分赛题 分析【2023.11.18】 文章目录 单选题tpcds模式中存在表customer,不能成功删除tpcds模式是( )以下哪个函数将圆转换成矩形( )下列哪个选项表示依赖该D…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
