C++知识点总结(6):高精度乘法真题代码
一、高精度数 × 低精度数
#include <iostream>
#include <cstring>
using namespace std;int main()
{// 存储并输入两个数字 char a_str[1005] = {};long long b;cin >> a_str >> b;// 特例先行:结果是0的情况if (a == 0 || b == 0){cout << 0;return 0;} // 转换第一个高精度数 int a[1005] = {};int len_a = strlen(a_str);for (int i = 0; i <= len_a-1; i++){a[len_a-i-1] = a_str[i] - 48;}// 计算int len_ans = len_a;long long ans[1005] = {};long long in = 0;for (int i = 0; i <= len_ans-1; i++){ans[i] = a[i] * b + in; // 存储数字 in = ans[i] / 10; // 得到进位 ans[i] %= 10; // 在对应的数位上保留实际得数的最后一位 }// 输出结果 while (in > 0) // 最高位处理 {ans[len_ans] = in % 10;len_ans++;in /= 10;}// 正常输出 for (int i = len_ans - 1; i >= 0; i--){cout << ans[i]; }return 0;
}二、高精度数 × 高精度数
#include <iostream>
#include <cstring>
using namespace std;int main()
{// 存储并输入两个数字 char a_str[1005] = {};char b_str[1005] = {};cin >> a_str >> b_str;// 转换高精度数 int a[1005] = {};int b[1005] = {};int len_a = strlen(a_str);int len_b = strlen(b_str);for (int i = 0; i <= len_a-1; i++){a[len_a-i-1] = a_str[i] - 48;}for (int i = 0; i <= len_b-1; i++){b[len_b-i-1] = b_str[i] - 48;}// 计算int ans[2010] = {};int in = 0;for (int j = 0; j <= len_b-1; j++){for (int i = 0; i <= len_a-1; i++){ans[i+j] = a[i] * b[j] + in + ans[i+j];in = ans[i+j] / 10;ans[i+j] %= 10; } // 最高位处理 ans[len_a+j] = in;in = 0; // 重置进位}// 正常输出int len_ans = len_a + len_b; // 结果的最大位数// 前导0while (ans[len_ans-1] == 0 && len_ans > 1){len_ans--;}for (int i = len_ans - 1; i >= 0; i--){cout << ans[i]; }return 0;
}三、高精度数的平方
#include <iostream>
#include <cstring>
using namespace std;int main()
{// 存储并输出两个数字 char a_str[1005] = {};char b_str[1005] = {};cin >> a_str;strcpy(b_str, a_str);// 转换高精度数 int a[1005] = {};int b[1005] = {};int len_a = strlen(a_str);int len_b = strlen(b_str);for (int i = 0; i <= len_a-1; i++){a[len_a-i-1] = a_str[i] - 48;}for (int i = 0; i <= len_b-1; i++){b[len_b-i-1] = b_str[i] - 48;}// 计算int ans[2010] = {};int in = 0;for (int j = 0; j <= len_b-1; j++){for (int i = 0; i <= len_a-1; i++){ans[i+j] = a[i] * b[j] + in + ans[i+j];in = ans[i+j] / 10;ans[i+j] %= 10; } // 最高位处理 ans[len_a+j] = in;in = 0; // 重置进位}// 正常输出int len_ans = len_a + len_b; // 结果的最大位数// 前导0while (ans[len_ans-1] == 0 && len_ans > 1){len_ans--;}for (int i = len_ans - 1; i >= 0; i--){cout << ans[i];}return 0;
}四、高精度阶乘
#include <iostream>
#include <cstring>
using namespace std;int main()
{// 输入int n;cin >> n;// 初始化计算相关变量 int in = 0;int ans[10005] = {1};int len_ans = 1;// 计算阶乘for (int num = 1; num < n; num++) // num是对应的因数 {// 高精度数 ×低精度数代码 for (int i = 0; i <= len_ans-1; i++) {ans[i] = ans[i] * num + in; // ans[i] = 上一轮的结果 * 下一个因数 + 上一次的进位 in = ans[i] / 10;ans[i] %= 10;}while (in){ans[len_ans] = in % 10;len_ans++;in /= 10;}}for (int i = 1; i <= len_ans; i++){cout << ans[i];}return 0;
} 建议结合课程学习:
戳进课程入口>>
相关文章:
:高精度乘法真题代码)
C++知识点总结(6):高精度乘法真题代码
一、高精度数 低精度数 #include <iostream> #include <cstring> using namespace std;int main() {// 存储并输入两个数字 char a_str[1005] {};long long b;cin >> a_str >> b;// 特例先行:结果是0的情况if (a 0 || b 0){cout <&…...

Polygon zkEVM的Dragon Fruit和Inca Berry升级
1. Polygon zkEVM的Dragon Fruit升级 2023年8月31日,Polygon zkEVM团队宣称启动了其Mainnet Beta的Dragon Fruit升级的10天timelock,预计将于2023年9月11日激活。 Dragon Fruit升级点有: 改进了网络支持了最新的以太坊opcode——PUSH0 1.…...

【计算机网络学习之路】网络基础1
文章目录 前言一. 计算机网络发展局域网和广域网 二. 网络协议三. OSI七层模型四. TCP/IP四层(五层)模型五. 计算机体系结构与网络协议栈六. 协议形式及局域网通信数据包封装与分用 七. 跨网络通信八. MAC地址与网络通信的理解结束语 前言 本系列文章是…...

HTTP/2.0协议详解
前言 HTTP/2.0:互联网通信的革新标准 随着互联网技术的飞速发展,HTTP协议作为互联网应用最广泛的通信协议,也在不断演进和优化。HTTP/2.0是HTTP协议的最新版本,它旨在提供更高效、更安全、更快速的互联网连接。 一、HTTP/2.0的优…...

Python中的Random模块详解:生成随机数与高级应用
在Python编程中,随机数生成是许多应用的基础之一。random模块为我们提供了生成伪随机数的丰富工具,从简单的随机数生成到复杂的应用场景,都有很多功能可以探索。本文将深入介绍random模块的各个方面,通过详实的示例代码࿰…...
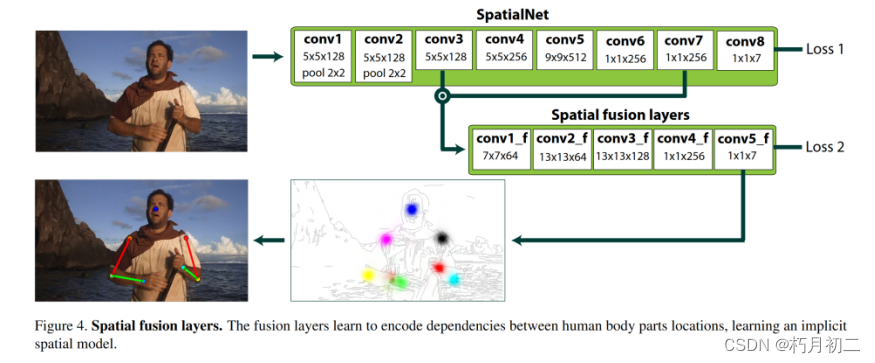
(论文阅读32/100)Flowing convnets for human pose estimation in videos
32.文献阅读笔记 简介 题目 Flowing convnets for human pose estimation in videos 作者 Tomas Pfister, James Charles, and Andrew Zisserman, ICCV, 2015. 原文链接 https://arxiv.org/pdf/1506.02897.pdf 关键词 Human Pose Estimation in Videos 研究问题 视频…...
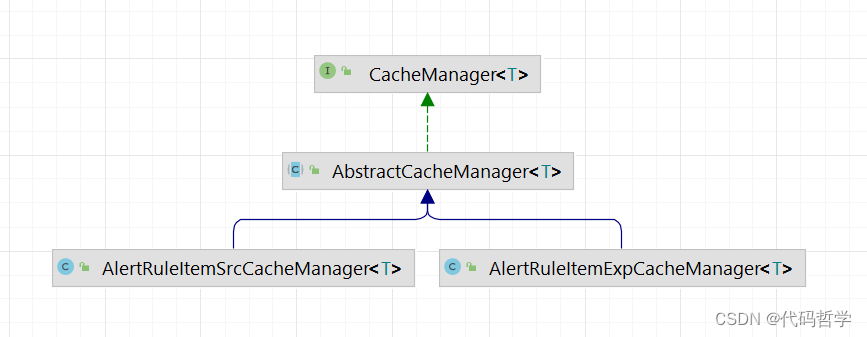
【设计一个缓存--针对各种类型的缓存】
设计一个缓存--针对各种类型的缓存 1. 设计顶层接口2. 设计抽象类 -- AbstractCacheManager3. 具体子类3.1 -- AlertRuleItemExpCacheManager3.2 -- AlertRuleItemSrcCacheManager 4. 类图关系 1. 设计顶层接口 // 定义为一个泛型接口,提供给抽象类使用 public interface Cach…...

Django部署时静态文件配置的坑
Django部署时静态文件配置配置的坑 近期有个需求是用django进行开发部署,结果发现静态文件配置的坑是真的多,另外网上很多的内容也讲不清楚原理,就是这样这样,又那样那样,进了不少坑,这里记录一下关于css,…...

Android---网络编程优化
网络请求操作是一个 App 的重要组成部分,程序大多数问题都是和网络请求有关。使用 OkHttp 框架后,可以通过 EventListener 来查看一次网络请求的详细情况。一次完整的网络请求会包含以下几个步骤。 也就是说,一次网络请求的操作是从 DNS 解析…...

《算法通关村——不简单的字符串转换问题》
《算法通关村——不简单的字符串转换问题》 8. 字符串转换整数 (atoi) 请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C 中的 atoi 函数)。 函数 myAtoi(string s) 的算法如下: 读入…...
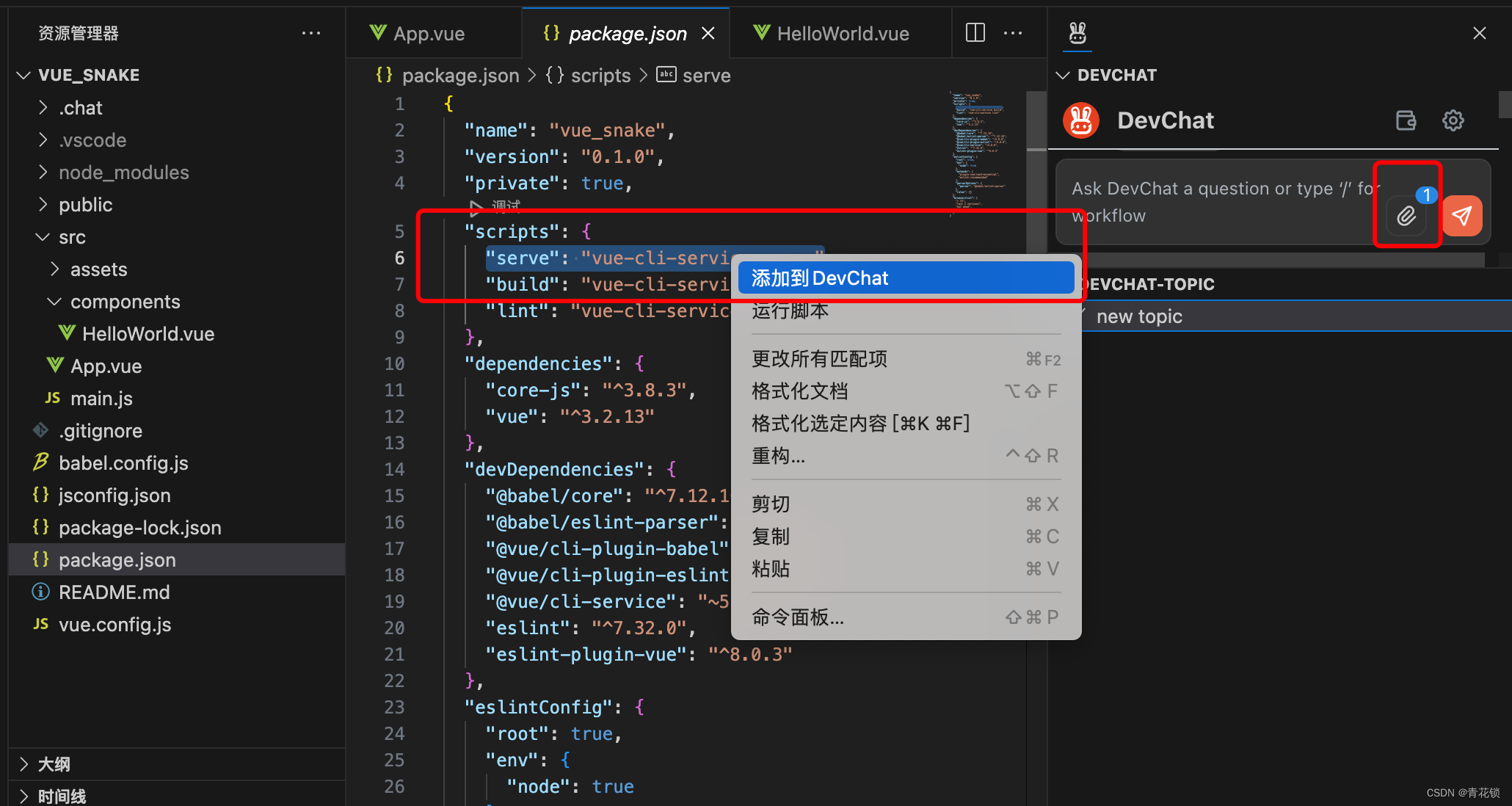
给VSCode插上一双AI的翅膀
#AI编程助手哪家好?DevChat“真”好用# 文章目录 前言一、安装DevChat1.1、访问地址1.2、注册1.3、在VSCode里安装DevChat插件1.3.1、未安装状态1.3.2、已安装状态 二、设置Access Key2.1. 点击左下角管理(“齿轮”图标)—命令面板ÿ…...

2023年亚太杯数学建模思路 - 案例:异常检测
文章目录 赛题思路一、简介 -- 关于异常检测异常检测监督学习 二、异常检测算法2. 箱线图分析3. 基于距离/密度4. 基于划分思想 建模资料 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 一、简介 – 关于异常…...
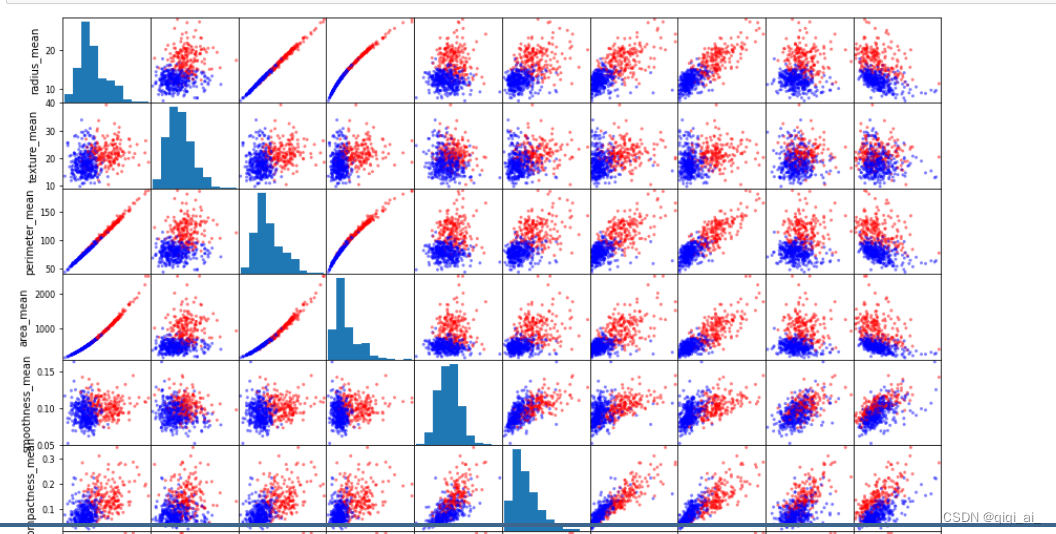
机器学习的医疗乳腺癌数据的乳腺癌疾病预测
项目视频讲解:基于机器学习的医疗乳腺癌数据的乳腺癌疾病预测 完整代码数据分享_哔哩哔哩_bilibili 效果演示: 代码: #第一步!导入我们需要的工具 import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns %matplotlib inlin…...

解析:什么是生成式AI?与其他类型的AI有何不同?
原创 | 文 BFT机器人 快速浏览一下头条新闻,你会发现生成式AI似乎无处不在。事实上,一些新闻标题甚至可能是通过生成式AI编写的,例如OpenAI旗下的ChatGPT,这个聊天机器人已经展现出了生成看起来像人类所写文本的惊人能力。 当人们…...

国产化项目改造:使用达梦数据库和东方通组件部署,前后端分离框架
前提:前后端分离前后端包都要用war包。 1、springboot后端改变war包 pom文件添加 <packaging>war</packaging>添加依赖,并且支持tomcat<!-- war包 --><dependency><groupId>org.springframework.boot</groupId><…...
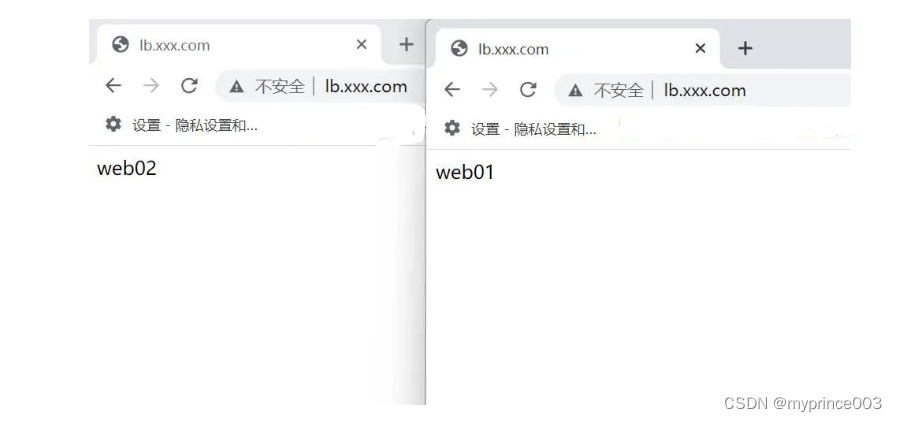
Nginx实现负载均衡
Nginx实现负载均衡 负载均衡的作用 1、解决单点故障,让web服务器构成一个集群 2、将请求平均下发给后端的web服务器 负载均衡的软硬件介绍 负载均衡软件: # nginx 四层负载均衡:stream(nginx 1.9版本以后有stream模块&#x…...
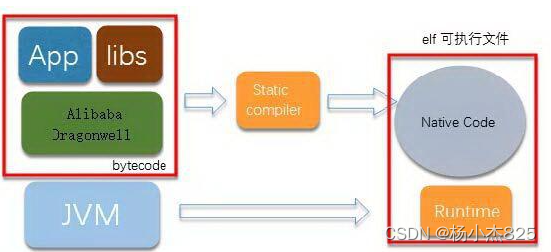
SpringCloud 2022有哪些变化
目录 前提条件 AOT支持 Spring Native支持 前提条件 Spring Cloud 2022.0.0是构建在Spring Framework 6.0和Spring Boot 3.0 之上的一S个主要版本。 JDK要求最低需要是Java 17J2EE要求最低需要Jakarta EE 9 AOT支持 Spring cloud 2022支持AOT编译,它是将程序源…...

如何快速本地搭建悟空CRM结合内网穿透工具高效远程办公
🌈个人主页:聆风吟 🔥系列专栏:数据结构、Cpolar杂谈 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. 无需公网IP,使用cpolar实现悟空CRM远程访问二. 通过公网来访问公司…...

Docker打包Python项目
1. 简介 Docker是一种开源的容器化平台,可以将应用程序及其依赖项打包到一个轻量级、可移植的容器中。通过使用Docker,可以简化Python项目的部署和运行,提高开发效率和应用程序的可移植性。 本文将介绍如何使用Docker来打包Python项目。我们…...

【Java并发编程一】并发与并行
为什么引入并发 摩尔定理逐渐失效,单核性能很难提升,通过组合多核性能来进一步满足实际需要,从而引入并发编程。在大部分场景下,并行是由于串行的,并行可以优化非关键节点的时间消耗。 并发的三大特性 原子性 某个…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
