当前位置： 首页 > news >正文

测不准原理

news 2026/2/9 16:52:38
  • 测不准原理

\begin{matrix} |\Psi>=\sum_n|\psi_n><\psi_n|\Psi>\\ =\sum_nc_n|\psi>\\ c_n=<\psi_n|\Psi>\\ =\int \psi_n^* \Psi dx \end{matrix}

算符的对易关系

  • commutation relation [\hat{A},\hat{B}]\equiv \hat{A}\hat{B}-\hat{B}\hat{A}

\begin{matrix} [r_a,p_a]=i\hbar\\ [r_a,p_b]=0\\ [p_a,p_b]=0\\ \end{matrix}

\begin{matrix} [L_x,L_y]=i\hbar L_z\\ [L_y,L_z]=i\hbar L_x\\ [L_z,L_z]=i\hbar L_y\\ \end{matrix}

\begin{matrix} [L_x,y]=i\hbar z\\ [L_y,z]=i\hbar x\\ [L_z,x]=i\hbar y\\ \end{matrix}

\begin{matrix} [L_x,z]=-i\hbar y\\ [L_y,x]=-i\hbar z\\ [L_z,y]=-i\hbar x\\ \end{matrix}

[L_i,r_i]=0

[L^2,L_x]=[L^2,L_y]=[L^2,L_z]=0

测不准原理的矢量推导

Schwarz inequality:|\langle\psi|\phi\rangle|^2\leq \langle\psi|\psi\rangle\langle\phi|\phi\rangle

设对易关系：AB-BA=iC

设一个新态：|\phi\rangle=(A+i\lambda B)|\psi\rangle

投影：\langle\psi|\phi\rangle=\langle\psi|A|\psi\rangle+i\lambda\langle\psi|B|\psi\rangle=\langle A\rangle+i\lambda \langle B\rangle

那么有：|\langle\psi|\phi\rangle|^2=\langle A\rangle^2+\lambda^2\langle B\rangle^2

\langle\phi|\phi\rangle=\langle\psi|(A^+-i\lambda B^+)(A+i\lambda B)\psi\rangle=\langle A^2\rangle+\lambda^2\langle B^2\rangle-\lambda\langle C\rangle

代回Schwarz inequality 即可证明：\Delta A\Delta B\geq \frac{\langle C\rangle}{2}

相关文章：

测不准原理

测不准原理 算符的对易关系 commutation relation 测不准原理的矢量推导 Schwarz inequality: 设对易关系&#xff1a; 设一个新态&#xff1a; 投影&#xff1a; 那么有&#xff1a; 代回Schwarz inequality 即可证明&#xff1a;...

编程日记 2023/11/19 5:35:51

微机原理_12

一、单项选择题(本大题共15小题,每小题3分&#xff0c;共45分。在每小题给出的四个备选项中&#xff0c;选出一个正确的答案。〕 十进制正数56的 8位二进制补码是()。 A. 00011001 B. 10100110 C. 10011001 D. 00100110 若栈顶的物理地址为20100H&#xff0c;当执行完指令PUSH…...

编程日记 2023/11/19 5:34:51

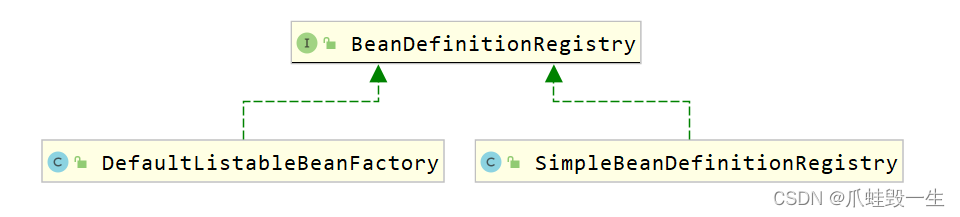
设计模式(5)-使用设计模式实现简易版springIoc

自定义简易版springIoc 1 spring使用回顾 自定义spring框架前&#xff0c;先回顾一下spring框架的使用&#xff0c;从而分析spring的核心&#xff0c;并对核心功能进行模拟。 数据访问层。定义UserDao接口及其子实现类 public interface UserDao {public void add(); }public…...

编程日记 2023/11/19 5:33:50

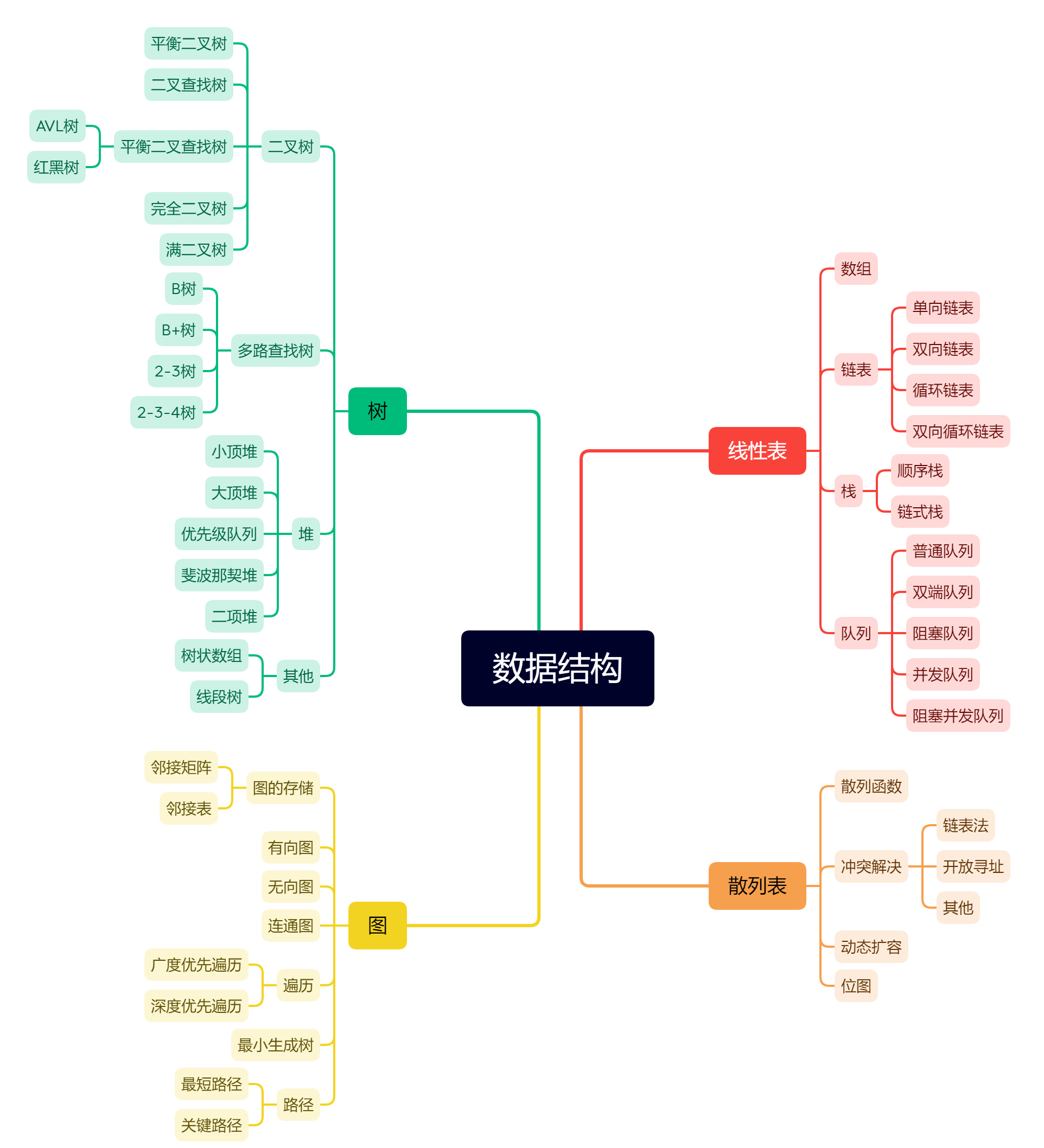
数据结构与集合源码

我是南城余&#xff01;阿里云开发者平台专家博士证书获得者&#xff01; 欢迎关注我的博客&#xff01;一同成长&#xff01; 一名从事运维开发的worker&#xff0c;记录分享学习。 专注于AI&#xff0c;运维开发&#xff0c;windows Linux 系统领域的分享&#xff01; 本…...

编程日记 2023/11/19 5:32:47

nodejs+vue面向中小学课堂教学辅助软件系统的设计与实现-微信小程序-安卓-python-PHP-计算机毕业设计

主要功能有&#xff0c;管理员通过后台会对此教学辅助进行审核&#xff0c;管理员在还可以进行首页、个人中心、学生管理、教师管理、班级信息管理、科目名称管理、课程信息管理、教学资料管理、作业信息管理、作业提交管理、作业成绩管理、在线考试管理、试题管理、考试管理、…...

编程日记 2023/11/19 5:31:46

智能配电系统解决方案

智能配电系统解决方案是一种集成了先进技术和智能化功能的配电系统&#xff0c;它能够提高电力系统的效率、可靠性和安全性。力安科技智能配电系统解决方案依托电易云-智慧电力物联网&#xff0c;具体实施的方案如下&#xff1a; 智能化设备和传感器&#xff1a;采用智能化的开…...

编程日记 2023/11/19 5:30:45

Python基础入门---conda 如何管理依赖包以及复制相同环境的

文章目录 创建虚拟环境：创建虚拟环境并指定Python版本：安装依赖包：从环境导出依赖包清单：从依赖包清单创建环境：复制环境：移植环境：在Conda中，你可以使用conda create命令来创建和管理虚拟环境，而使用conda install命令来安装和管理依赖包。以下是一些基本的命令和步骤…...

编程日记 2023/11/19 5:29:44

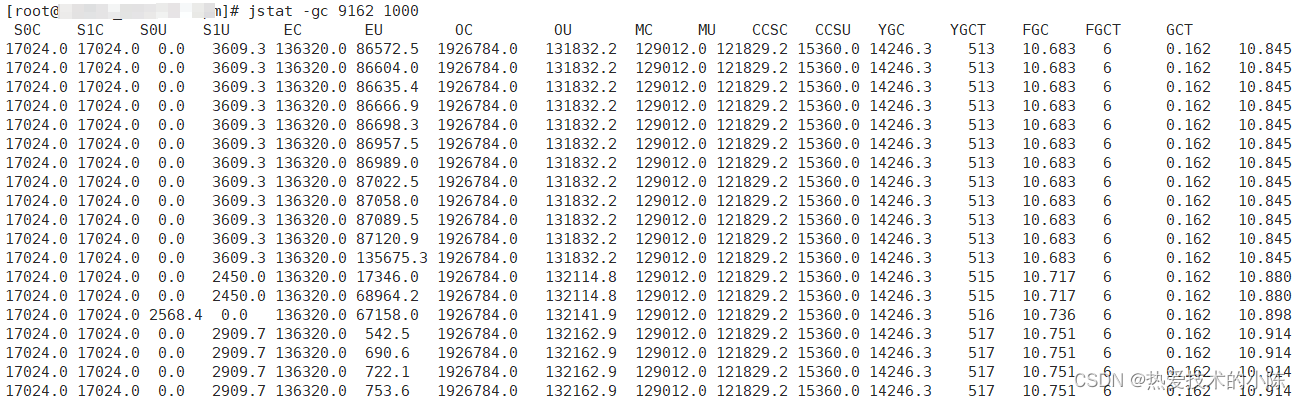
JVM jstat 查看内存新生代老年代回收情况，排查oom

jstat 命令 jstat - [-t] [-h] [ []] option&#xff1a;我们经常使用的选项有gc、gcutil vmid&#xff1a;java进程id interval&#xff1a;间隔时间&#xff0c;单位为毫秒 count&#xff1a;打印次数 每秒打印一次 jstat -gc 9162 1000S0C:年轻代第一个survivor的容量…...

编程日记 2023/11/19 5:28:43

Postman启动问题：Could not open Postman

Postman启动问题&#xff1a;Could not open Postman 状态&#xff0c;在单击Postman之后一直在转圈圈&#xff0c;无法正常启动。 细心的朋友会发现&#xff0c;右下角 会经常出现防火墙关闭等提示信息&#xff0c;表示该程序&#xff0c;在向外链接。 Error Could not open…...

编程日记 2023/11/19 5:27:42

Golang起步篇（Windows、Linux、mac三种系统安装配置go环境以及IDE推荐以及入门语法详细释义）

Golang起步篇 Golang起步篇一. 安装Go语言开发环境1. Wondows下搭建Go开发环境(1). 下载SDK工具包(2). 解压下载的压缩包&#xff0c;放到特定的目录下&#xff0c;我一般放在d:/programs下(路径不能有中文或者特殊符号如空格等)(3). 配置环境变量步骤1&#xff1a;先打开环境变…...

编程日记 2023/11/19 5:26:40

Error message “error:0308010C:digital envelope routines::unsupported“

1.降级到 Node.js v16。 您可以从 Node.js 的 website 重新安装当前的 LTS 版本。 您也可以使用 nvm。对于 Windows&#xff0c;请使用 nvm-windows。 2.启用传统 OpenSSL 提供程序。 在类 Unix 系统&#xff08;Linux、macOS、Git bash 等&#xff09;上&#xff1a; exp…...

编程日记 2023/11/19 5:25:39

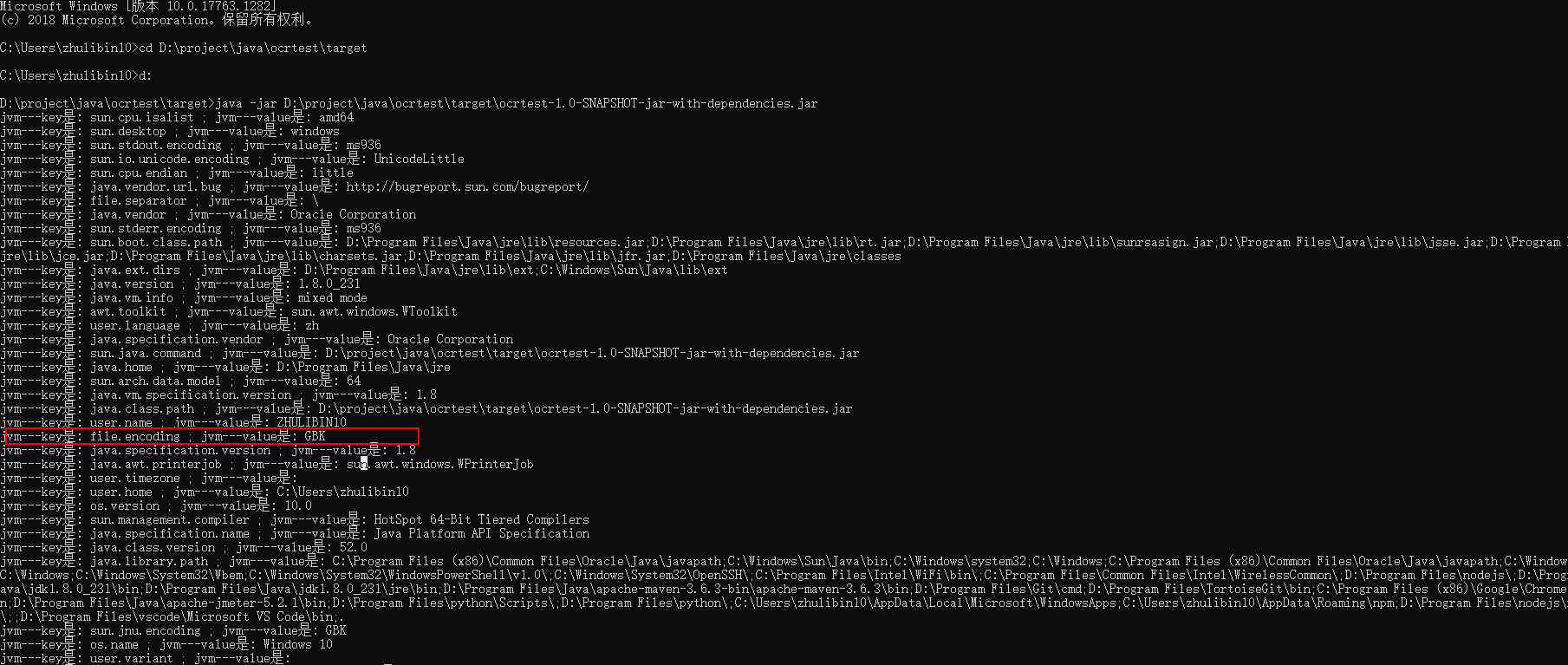
解决java在idea运行正常,但是打成jar包后中文乱码问题

目录 比如&#xff1a; 打包命令使用utf-8编码&#xff1a; 1.当在idea中编写的程序,运行一切正常.但是当被打成jar包时,执行的程序会中文乱码.产生问题的原因和解决方案是什么呢? 一.问题分析 分别使用idea和jar包形式打印出System中所有的jvm参数---代码如下: public static…...

编程日记 2023/11/19 5:24:38

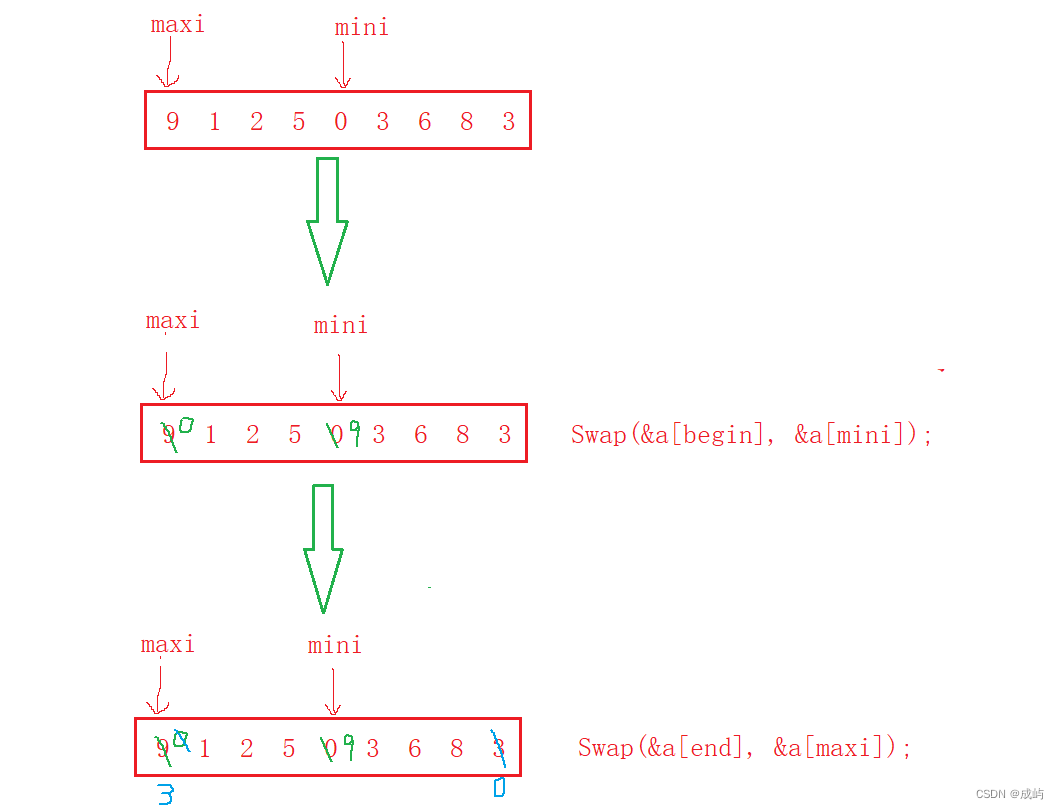
数据结构-插入排序+希尔排序+选择排序

目录 1.插入排序 插入排序的时间复杂度&#xff1a; 2.希尔排序 希尔排序的时间复杂度&#xff1a; 3.选择排序 选择排序的时间复杂度&#xff1a; 所谓排序&#xff0c;就是使一串记录&#xff0c;按照其中的某个或某些关键字的大小&#xff0c;递增或递减的排列起来的…...

编程日记 2023/11/19 5:23:37

微信小程序数据传递的方式-页面数据的存取

我们在把数据显示到页面的时候&#xff0c;为了实现良好的互动&#xff0c;都希望在用户点击某个栏目后&#xff0c;获取这个栏目的捆绑数据&#xff0c;然后执行后续的操作。 例如&#xff0c;从数据库里取出对应的记录后&#xff0c;显示在页面上&#xff0c;是一条条的大横条…...

编程日记 2023/11/19 5:22:35

Flutter 应用启动从闪屏页短暂黑屏再到第一个页面

由于应用初始状态启动会有白屏现象&#xff0c;便使用 flutter_native_splash 2.3.5 插件生成了启动相关的配置&#xff0c;并且按照示例使用了 import package:flutter_native_splash/flutter_native_splash.dart;void main() {WidgetsBinding widgetsBinding WidgetsFlutte…...

编程日记 2023/11/19 5:21:33

Linux+qt：获取.so自身的路径（利用dladdr）

目录 1、QDir::currentPath() 2、QAppllication::appllicationDirPath() 3、获取.so自身的路径&#xff08;利用dladdr&#xff09; Qt中&#xff0c;也有相关的接口获取程序的相关路径的。 先了解下相关的接口&#xff1a; 1、QDir::currentPath() &#xff08;1&#x…...

编程日记 2023/11/19 5:20:32

CSS特效014：模仿钟摆效果

CSS常用示例100专栏目录 本专栏记录的是经常使用的CSS示例与技巧&#xff0c;主要包含CSS布局&#xff0c;CSS特效&#xff0c;CSS花边信息三部分内容。其中CSS布局主要是列出一些常用的CSS布局信息点&#xff0c;CSS特效主要是一些动画示例&#xff0c;CSS花边是描述了一些CSS…...

编程日记 2023/11/19 5:19:30

计算机毕业设计选题推荐-个人健康微信小程序/安卓APP-项目实战

✨作者主页&#xff1a;IT研究室✨ 个人简介&#xff1a;曾从事计算机专业培训教学&#xff0c;擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Python…...

编程日记 2023/11/19 5:17:28

【自然语言处理（NLP）实战】LSTM网络实现中文文本情感分析（手把手与教学超详细）

目录 引言&#xff1a; 1.所有文件展示&#xff1a; 1.中文停用词数据&#xff08;hit_stopwords.txt)来源于&#xff1a; 2.其中data数据集为chinese_text_cnn-master.zip提取出的文件。点击链接进入github&#xff0c;点击Code、Download ZIP即可下载。 2.安装依赖库&am…...

编程日记 2023/11/19 5:16:27

迭代新品 | 第四代可燃气体监测仪，守护燃气管网安全快人一步

城市地下市政基础设施是城市有序运行的生命线&#xff0c;事关城市安全、健康运行和高质量发展。近年来&#xff0c;我国燃气事故多发、频发。2020、2021、2022 年分别发生燃气事故668、1140 起、802 起&#xff0c;造成92、106、66 人死亡&#xff0c;560、763、487 人受伤。尤…...

编程日记 2023/11/19 5:15:25

网络六边形受到攻击

大家读完觉得有帮助记得关注和点赞&#xff01;&#xff01;&#xff01; 抽象 现代智能交通系统 &#xff08;ITS&#xff09; 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 &#xff08;…...

编程新知 2026/2/8 5:22:04

Chapter03-Authentication vulnerabilities

文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

编程新知 2026/2/7 4:57:53

51c自动驾驶~合集58

我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留&#xff0c;CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制&#xff08;CCA-Attention&#xff09;&#xff0c;…...

编程新知 2026/2/5 4:25:15

【OSG学习笔记】Day 18: 碰撞检测与物理交互

物理引擎&#xff08;Physics Engine&#xff09; 物理引擎 是一种通过计算机模拟物理规律&#xff08;如力学、碰撞、重力、流体动力学等&#xff09;的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互&#xff0c;广泛应用于 游戏开发、动画制作、虚…...

编程新知 2026/2/4 2:08:30

DeepSeek 赋能智慧能源：微电网优化调度的智能革新路径

目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

编程新知 2025/11/20 2:48:44

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真

目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销&#xff0c;平衡网络负载&#xff0c;延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

编程新知 2026/2/6 5:38:46

Java如何权衡是使用无序的数组还是有序的数组

在 Java 中，选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南： ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

编程新知 2025/8/3 11:17:37

Qt Widget类解析与代码注释

#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码&#xff0c;写上注释 当然可以&#xff01;这段代码是 Qt …...

编程新知 2025/11/29 21:00:30

关于 WASM：1. WASM 基础原理

一、WASM 简介 1.1 WebAssembly 是什么&#xff1f; WebAssembly&#xff08;WASM&#xff09; 是一种能在现代浏览器中高效运行的二进制指令格式&#xff0c;它不是传统的编程语言&#xff0c;而是一种 低级字节码格式&#xff0c;可由高级语言&#xff08;如 C、C、Rust&am…...

编程新知 2025/11/19 10:53:07

【JavaSE】绘图与事件入门学习笔记

-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角&#xff0c;以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向&#xff0c;距离坐标原点x个像素;第二个是y坐标&#xff0c;表示当前位置为垂直方向&#xff0c;距离坐标原点y个像素。 坐标体系-像素 …...

编程新知 2025/12/19 20:46:15