数据结构-插入排序+希尔排序+选择排序
目录
1.插入排序
插入排序的时间复杂度:
2.希尔排序
希尔排序的时间复杂度:
3.选择排序
选择排序的时间复杂度:
所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。排序在生活中的作用很大,例如:某宝中的价格排行榜、销量排行榜,国内外的财富排行榜、院校排行榜等等,都是使用排序完成的。
下面我们看看常见的排序都有哪些:

1.插入排序
基本思想:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
实际中我们玩扑克牌时,就用了插入排序的思想:
插入排序的过程如下:
假设我们有如下一个数组:
具体实现代码如下:
while (end >= 0) {//挪数据if (tmp < a[end]){a[end + 1] = a[end];end--;}else{break;} } //交换数据 a[end + 1] = tmp;tmp中存放的是3,3小于10,10往后挪一位,3小于5,5往后挪一位......当end到2时,tmp小于2,退出循环,此时5 7 10都已经往后挪了一位,数组中的元素应该是:2 5 5 7 10,我们把tmp中存放的3和2后面的5交换即可。
以上只是一个数据的插入排序,要实现整个数组的排序,我们需要对数组的每个数据都往前插入排序一下:
void InsertSort(int* a, int n) {for (int i = 1; i < n; i++){int end = i - 1;int tmp = a[i];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;} }
插入排序的时间复杂度:
假设我们要排升序,当要排的数据刚好是降序时,时间复杂度最大,为O(N^2),因为此时排序的次数是等差数列。
当要排的数据刚好是升序的时候,是最好的情况,时间复杂度最小,但是我们在排之前并不知道数据是升序,所以至少要排N次,时间复杂度为O(N)。
总结一下:
时间复杂度(最好):O(N^2)
时间复杂度(最坏):O(N)
而我们之前学过的冒泡排序,时间复杂度是O(N^2),所以插入排序优于冒泡排序。
2.希尔排序
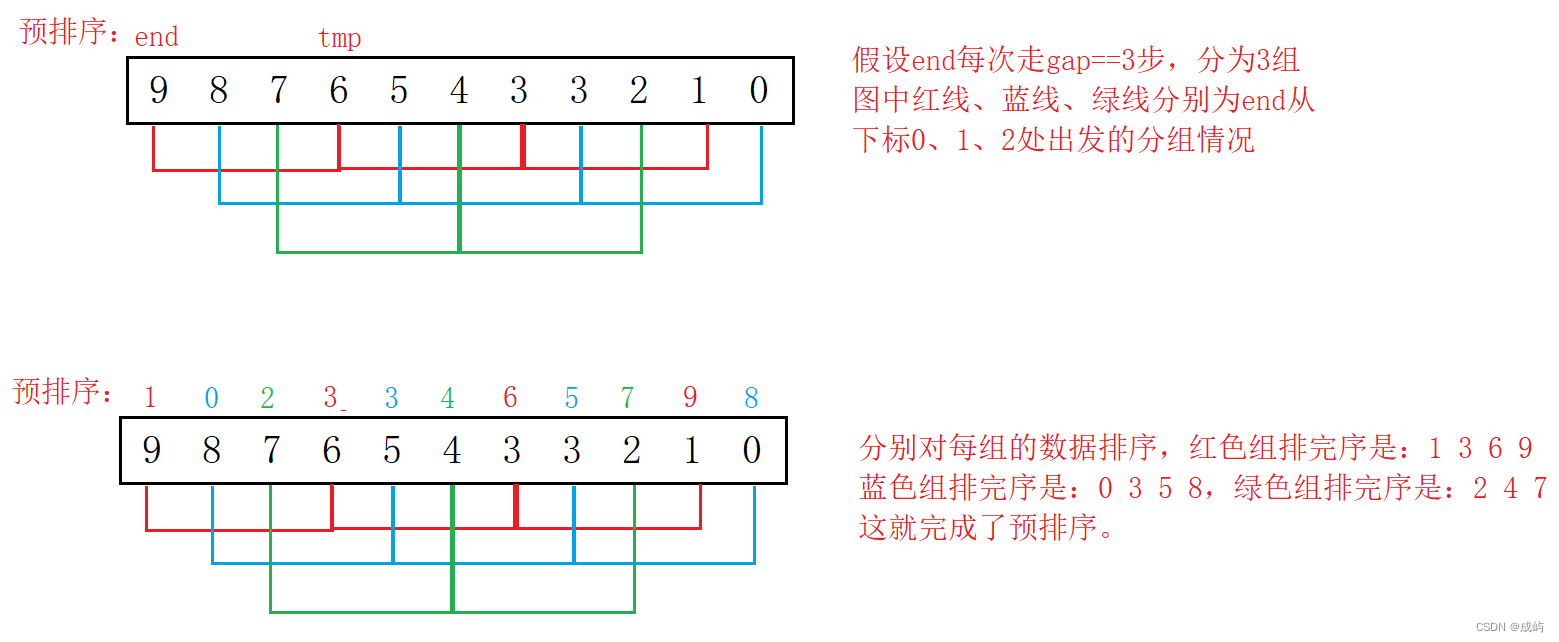
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数gap,把待排序文件中所有数据分成n/gap个组,所有距离为gap的数据分在同一组内,并对每一组内的数据进行排序,最后再进行一次gap=1的分组和排序。
希尔排序有两个过程:
1. 预排序 -- 使接近有序。
2. 插入排序
即先进行预排序是数据接近有序,然后使用一次插入排序,使数据有序。希尔排序实际就是对插入排序的优化。
预排序:
下面我们先来对红色组进行排序:
for (int i = 0; i < n - gap; i+=gap) {int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end = end - gap;}else{break;}}a[end + gap] = tmp; }注意下标 i 不能越界,所以 i < n - gap。
以上代码只能完成对红色组的排序,下面我们来将三个组都排好序:
只需在外面再加一层循环即可。
for (int j = 0; j < gap; j++) {for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end = end - gap;}else{break;}}a[end + gap] = tmp;} }这样三组数据都排好序,完成了预排序,但是上述代码有似乎还可以简化:
for (int i = 0; i < n - gap; i++) {int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end = end - gap;}else{break;}}a[end + gap] = tmp; }只需将i+=gap,改为i++即可,当i+=gap时,我们是将三组分开排序的,先排完红色组,再排蓝色组,最后排绿色组,而当i++时,我们是多组并排的方式,这样明显效率更高。
插入排序:
以上就是预排序的过程,预排序完,数据变成了:1 02 3 3 4 6 5 7 9 8,还需要一次插入排序,现在我们先来思考一个问题,gap的值只能给3吗?
当然不是,gap可以任意给值,只不过,给的值不同,预排序出来的数据次序就不同。
我们可以令gap=n,gap=gap/3+1, 这样每次使用的gap都在变化,而且能确保最后一次的gap一定是1,也就确保了最后一次一定进行的是插入排序。
最终代码如下:
void ShellSort(int* a, int n) {//gap > 1 预排序//gap = 1 直接插入排序int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}} }
希尔排序的时间复杂度:
希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些书中给出的希尔排序的时间复杂度都不固定:
《数据结构(C语言版)》--- 严蔚敏

《数据结构-用面相对象方法与C++描述》--- 殷人昆

3.选择排序
基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
选择排序过程如下图所示:
上图中是把待选数据遍历一遍,每次选出最小的数据放在前面,其实我们可以对其优化一下:把待选数据遍历一遍,每次同时选出最大和最小的数据,把最小的数据放在前面,最大的数据放在后面。
代码如下:
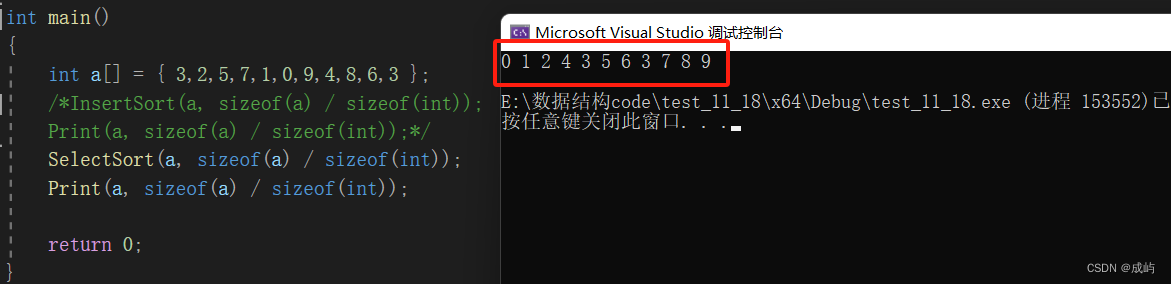
void Swap(int* p1, int* p2) {int tmp = *p1;*p1 = *p2;*p2 = tmp; } void SelectSort(int* a, int n) {int begin = 0;int end = n - 1;int mini = begin;int maxi = end;while (begin<end){for (int i = begin; i <= end; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[begin], &a[mini]);Swap(&a[end], &a[maxi]);begin++;end--;} }问题来了,上述代码对吗?
运行一下就会发现:
诶?不对啊,那到底哪里出错了呢?
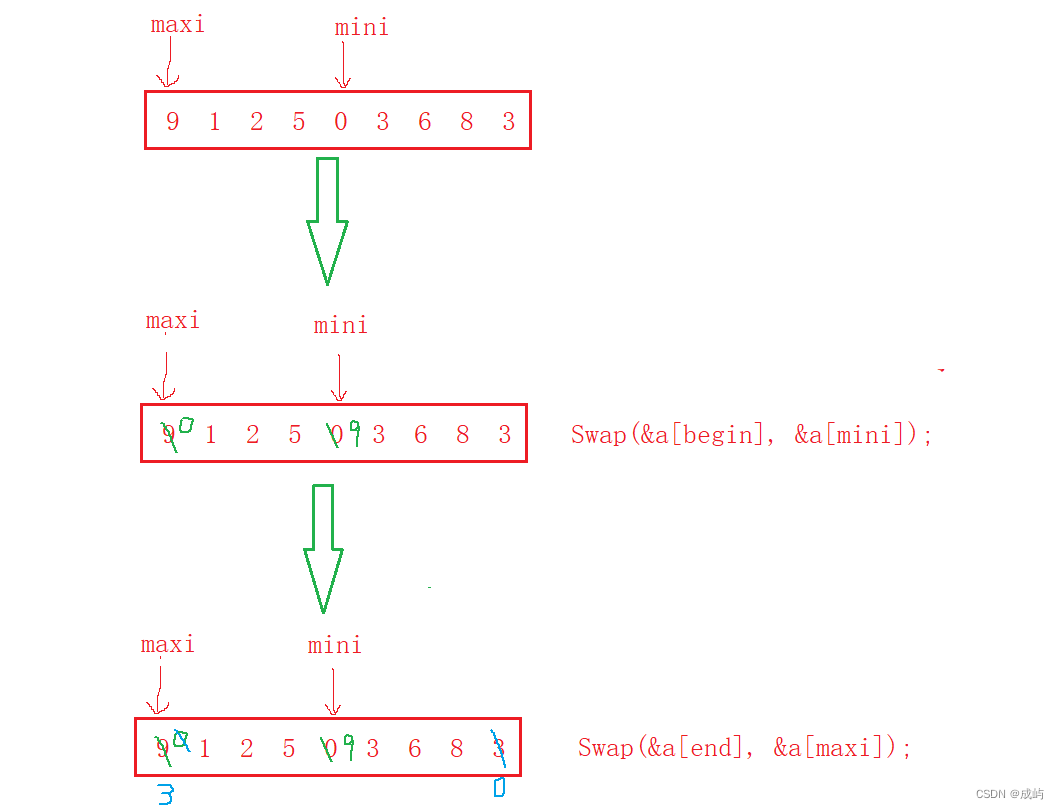
下面我们举个极端的例子:
经过遍历以后发现,最大数的下标maxi和begin重合了,那我们交换时就出现问题了,最小数0确实放在了前面,但是最大数的位置也变了,下面再想把最大数放在后面,此时的下标就不能再用了,所以我们在交换a[begin]和a[mini]的值后,要将最大数的下标更改:
void Swap(int* p1, int* p2) {int tmp = *p1;*p1 = *p2;*p2 = tmp; } void SelectSort(int* a, int n) {int begin = 0;int end = n - 1;while (begin < end){int mini = begin;int maxi = end;for (int i = begin; i <= end; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[begin], &a[mini]);//如果发生重叠,就更改下标if (begin == maxi){maxi = mini;}Swap(&a[end], &a[maxi]);begin++;end--;} }
选择排序的时间复杂度:
选择排序的时间复杂度很简单,就是O(N^2),它每排一个数据都要遍历后面的数据一遍,遍历次数是等差数列,前面的章节中学过,等差数列的时间复杂度是O(N^2),虽然上述的代码进行优化,将遍历次数减半为N^2/2,但是量级没变,还是O(N^2)。
今天就学习这三种排序,冒泡排序、堆排序在之前的章节中已经讲解过,下节我们继续学习快速排序和归并排序,未完待续。。。
相关文章:
数据结构-插入排序+希尔排序+选择排序
目录 1.插入排序 插入排序的时间复杂度: 2.希尔排序 希尔排序的时间复杂度: 3.选择排序 选择排序的时间复杂度: 所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的…...

微信小程序数据传递的方式-页面数据的存取
我们在把数据显示到页面的时候,为了实现良好的互动,都希望在用户点击某个栏目后,获取这个栏目的捆绑数据,然后执行后续的操作。 例如,从数据库里取出对应的记录后,显示在页面上,是一条条的大横条…...

Flutter 应用启动从闪屏页短暂黑屏再到第一个页面
由于应用初始状态启动会有白屏现象,便使用 flutter_native_splash 2.3.5 插件生成了启动相关的配置,并且按照示例使用了 import package:flutter_native_splash/flutter_native_splash.dart;void main() {WidgetsBinding widgetsBinding WidgetsFlutte…...
)
Linux+qt:获取.so自身的路径(利用dladdr)
目录 1、QDir::currentPath() 2、QAppllication::appllicationDirPath() 3、获取.so自身的路径(利用dladdr) Qt中,也有相关的接口获取程序的相关路径的。 先了解下相关的接口: 1、QDir::currentPath() (1&#x…...

CSS特效014:模仿钟摆效果
CSS常用示例100专栏目录 本专栏记录的是经常使用的CSS示例与技巧,主要包含CSS布局,CSS特效,CSS花边信息三部分内容。其中CSS布局主要是列出一些常用的CSS布局信息点,CSS特效主要是一些动画示例,CSS花边是描述了一些CSS…...

计算机毕业设计选题推荐-个人健康微信小程序/安卓APP-项目实战
✨作者主页:IT研究室✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Python…...

【自然语言处理(NLP)实战】LSTM网络实现中文文本情感分析(手把手与教学超详细)
目录 引言: 1.所有文件展示: 1.中文停用词数据(hit_stopwords.txt)来源于: 2.其中data数据集为chinese_text_cnn-master.zip提取出的文件。点击链接进入github,点击Code、Download ZIP即可下载。 2.安装依赖库&am…...

迭代新品 | 第四代可燃气体监测仪,守护燃气管网安全快人一步
城市地下市政基础设施是城市有序运行的生命线,事关城市安全、健康运行和高质量发展。近年来,我国燃气事故多发、频发。2020、2021、2022 年分别发生燃气事故668、1140 起、802 起,造成92、106、66 人死亡,560、763、487 人受伤。尤…...

【教3妹学编程-java基础6】详解父子类变量、代码块、构造函数执行顺序
-----------------第二天------------------------ 本文先论述父子类变量、代码块、构造函数执行顺序的结论, 然后通过举例论证,接着再扩展,彻底搞懂静态代码块、动态代码块、构造函数、父子类、类加载机制等知识体系。 温故而知新ÿ…...

深度学习中文汉字识别 计算机竞赛
文章目录 0 前言1 数据集合2 网络构建3 模型训练4 模型性能评估5 文字预测6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习中文汉字识别 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐…...
从零开始 通义千问大模型本地化到阿里云通义千问API调用
从零开始 通义千问大模型本地化到阿里云通义千问API调用 一、通义千问大模型介绍 何为“通义千问”? “通义千问大模型”是阿里云推出的一个超大规模的语言模型,具有强大的归纳和理解能力,可以处理各种自然语言处理任务,包括但…...
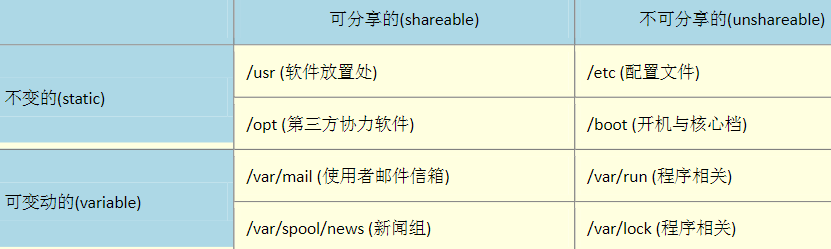
Linux(3):Linux 的文件权限与目录配置
把具有相同的账户放入到一个组里面,这个组就是这两个账户的 群组 。在访问资源(操作系统中计算机的资源)时,可以让这个组里面的所有用户都具有访问权限。 每个账号都可以有多个群组的支持。 在我们Liux 系统当中,默认的…...
Linux进程——exec族函数、exec族函数与fork函数的配合
exec族函数解析 作用 我们用fork函数创建新进程后,经常会在新进程中调用exec函数去执行另外一个程序。当进程调用exec函数时,该进程被完全替换为新程序。因为调用exec函数并不创建新进程,所以前后进程的ID并没有改变。 功能 在调用进程内部…...

客户端缓存技术
客户端缓存技术主要有以下几种: 内存缓存:客户端(如浏览器)会将请求到的资源(如HTML页面、图片文件等)存储在内存中,以便在再次访问相同资源时可以快速获取,减少向服务器的请求次数…...

Leetcode -2
Leetcode Leetcode -263.丑数Leetcode -268.丢失的数字 Leetcode -263.丑数 题目:丑数就是只包含质因数 2、3 和 5 的正整数。 给你一个整数 n ,请你判断 n 是否为 丑数 。如果是,返回 true ;否则,返回 false 。 示例…...
)
使用 DFS 轻松求解数独难题(C++ 的一个简单实现)
起因 都说懒惰是第一生产力,最近在玩数独游戏的时候,总会遇到拆解数独比较复杂的情况,就想着自己写个代码解题,解放双手。所以很快就写了一个简单的代码求解经典数独。拿来跑了几个最高难度的数独发现确实很爽!虽说是…...
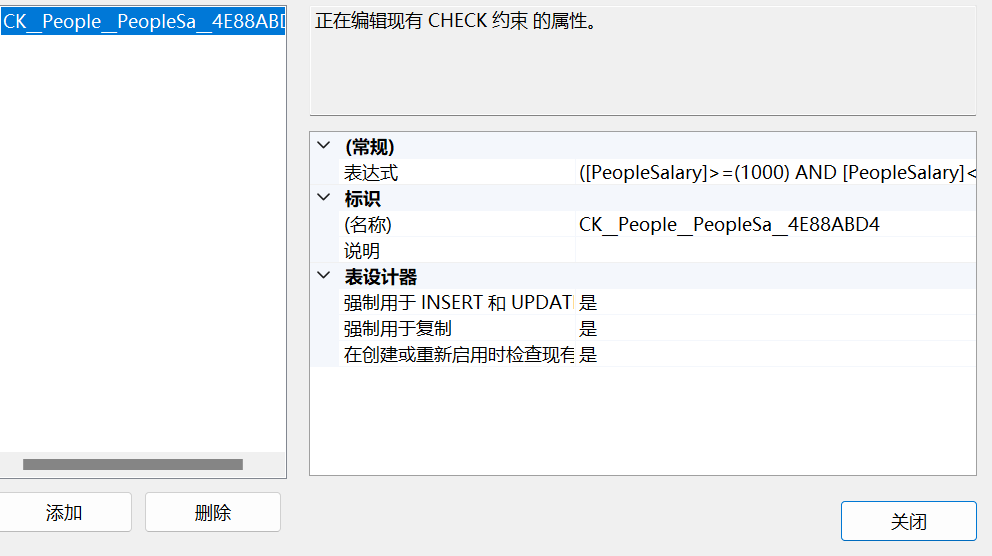
【SQL server】 表结构的约束和维护
表结构的约束和维护 修改表结构 (1)添加列 (2)删除列 (3)修改列alter table 表名 add 新列名 数据类型给员工表添加一列邮箱 alter table People add PeopleMail varchar(200)删除列 alter table People drop column PeopleMain修改列 alter table 表名 alter column 列名 数据…...

竞赛 题目:基于大数据的用户画像分析系统 数据分析 开题
文章目录 1 前言2 用户画像分析概述2.1 用户画像构建的相关技术2.2 标签体系2.3 标签优先级 3 实站 - 百货商场用户画像描述与价值分析3.1 数据格式3.2 数据预处理3.3 会员年龄构成3.4 订单占比 消费画像3.5 季度偏好画像3.6 会员用户画像与特征3.6.1 构建会员用户业务特征标签…...

Vue3-ref、reactive函数的watch
Vue3-ref、reactive函数的watch ref函数的watch 原理:监视某个属性的变化。当被监视的属性一旦发生改变时,执行某段代码。watch 属性中的数据需要具有响应式watch 属性可以使用箭头函数watch 属性可以监视一个或者多个响应式数据,并且可以配…...

【智能家居项目】FreeRTOS版本——多任务系统中使用DHT11 | 获取SNTP服务器时间 | 重新设计功能框架
🐱作者:一只大喵咪1201 🐱专栏:《智能家居项目》 🔥格言:你只管努力,剩下的交给时间! 目录 🍓多任务系统中使用DHT11🍅关闭调度器🍅使用中断 &am…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...