ai绘画部署教程
在部署AI绘画Web环境的过程中,你提供了一些关键步骤。以下是一些详细说明:
1. 克隆webui
首先,通过以下命令从GitHub上克隆webui的代码:
git clone https://github.com/AUTOMATIC1111/stable-diffusion-webui
这将下载webui的源代码到你的本地机器。
2. 创建虚拟Python环境
接下来,为了隔离项目的依赖,你创建了一个虚拟Python环境。这有助于确保项目所需的库和缓存文件不会混杂在全局Python环境中。
virtualenv cms
3. 激活虚拟环境
激活虚拟环境的命令如下:
F:\sd AI\py38\Scripts\activate.bat
这将使你进入虚拟环境,所有后续的Python包的安装都将在此环境中进行。
4. 安装CPU运算库(如果没有显卡)
如果你的系统没有显卡,需要安装支持CPU运算的库。在你的虚拟环境中运行以下命令:
pip install -i https://mirrors.aliyun.com/pypi/simple some-package torch torchvision torchaudio
5. 运行
直接运行webui-user.bat应该能够自动识别并启动应用程序。
6. 无显卡或CUDA
如果你的系统没有显卡或者不支持CUDA,你可以在webui-user.bat文件中进行修改,添加以下选项:
set COMMANDLINE_ARGS= --lowvram --precision full --no-half --skip-torch-cuda-test
这样可以确保应用程序在没有CUDA支持的情况下运行。
通过按照这些步骤,你应该能够成功部署AI绘画Web环境并运行应用程序。
相关文章:

ai绘画部署教程
在部署AI绘画Web环境的过程中,你提供了一些关键步骤。以下是一些详细说明: 1. 克隆webui 首先,通过以下命令从GitHub上克隆webui的代码: git clone https://github.com/AUTOMATIC1111/stable-diffusion-webui 这将下载webui的源…...

策略模式的应用——应对频繁的需求变更
秋招结束后,间接性堕落了一段时间,学习几乎停止下来了。内心甚是焦灼,感觉生活很无趣!为了在参加工作后能够快速上手和成为一名优秀的中级开发者,从这篇文章开始将不断学习优秀的编码经验,学习是永无止境的…...

qt-C++笔记之treeWidget初次使用
qt-C笔记之treeWidget初次使用 code review! 文章目录 qt-C笔记之treeWidget初次使用1.运行2.文件结构3.main.cpp4.widget.h5.widget.cpp6.widget.ui7.main.qrc8.qt_widget_test.pro9.options.png 1.运行 2.文件结构 3.main.cpp 代码 #include "widget.h"#include…...

SQL零基础入门教程,贼拉详细!贼拉简单! 速通数据库期末考!(八)
FULL OUTER JOIN 除了前面讲到的 INNER JOIN(内连接)、LEFT JOIN(左连接)、RIGHT JOIN(右连接),还有另外一种关联方式,即 FULL OUTER JOIN(全外连接) FULL O…...
)
C语言编程陷阱(八)
陷阱36:不要使用指针作为函数的返回值 有时候,我们可能想要用一个函数来返回一个指针,比如返回一个动态分配的内存,或者返回一个数组的某个元素的地址。但是,如果我们不小心,我们可能会犯一个很常见的错误,就是返回一个局部变量的地址。例如,看看下面的代码: #inclu…...
客户端性能优化实践
背景 双十一大促时,客户客服那边反馈商品信息加载卡顿,在不断有订单咨询时,甚至出现了商品信息一直处于加载状态的情况,显然,在这种高峰期接待客户时,是没法进行正常的接待工作的。 起初,页面一…...

mysql使用--表达式和函数
1.表达式 如:11,一般包含操作数,运算符。 _1.操作数 MYSQL中最常用的操作数有以下几种 (1).常数 (2).列名,针对某个具体的表,它的列名可被当作表达式的一部分 (3).函数调用 一个函数用于完成某个特定的功能。比如NOW()…...
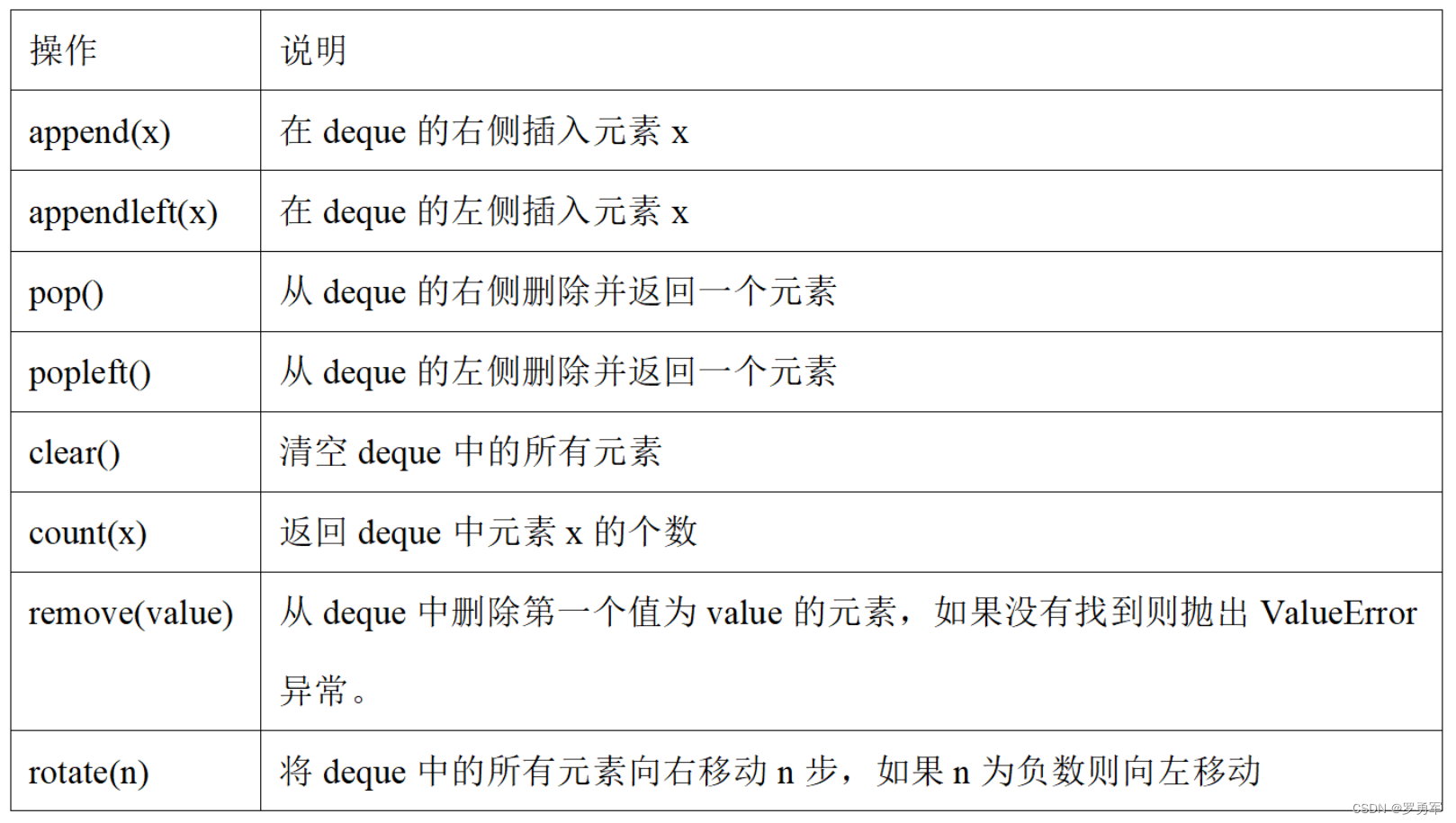
<蓝桥杯软件赛>零基础备赛20周--第6周--数组和队列
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集 20周的完整安排请点击:20周计划 每周发1个博客,共20周(读者可以按…...

软件开发、网络空间安全、人工智能三个方向的就业和前景怎么样?哪个方向更值得学习?
软件开发、网络空间安全、人工智能这三个方向都是当前及未来的热门领域,每个领域都有各自的就业前景和价值,以下是对这三个方向的分析: 1、软件开发: 就业前景:随着信息化的加速,软件开发的需求日益增长。…...

新增文章分类
pojo.Category package com.lin.springboot01.pojo;import jakarta.validation.constraints.NotEmpty; import lombok.Data;import java.time.LocalDateTime;Data public class Category {private Integer id;//主键NotEmptyprivate String categoryName;//分类名称NotEmptypr…...

选硬币该用动态规划
选硬币: 现有面值分别为1角1分,5分,1分的硬币,请给出找1角5分钱的最佳方案。 #include <iostream> #include <vector>std::vector<int> findChange(int amount) {std::vector<int> coins {11, 5, 1}; /…...

LeetCode 2342. 数位和相等数对的最大和:哈希表
【LetMeFly】2342.数位和相等数对的最大和:哈希表 力扣题目链接:https://leetcode.cn/problems/max-sum-of-a-pair-with-equal-sum-of-digits/ 给你一个下标从 0 开始的数组 nums ,数组中的元素都是 正 整数。请你选出两个下标 i 和 j&…...
Vulkan渲染引擎开发教程 一、开发环境搭建
一 安装 Vulkan SDK Vulkan SDK 就是我们要搞的图形接口 首先到官网下载SDK并安装 https://vulkan.lunarg.com/sdk/home 二 安装 GLFW 窗口库 GLFW是个跨平台的小型窗口库,也就是显示窗口,图形的载体 去主页下载并安装,https://www.glfw.…...
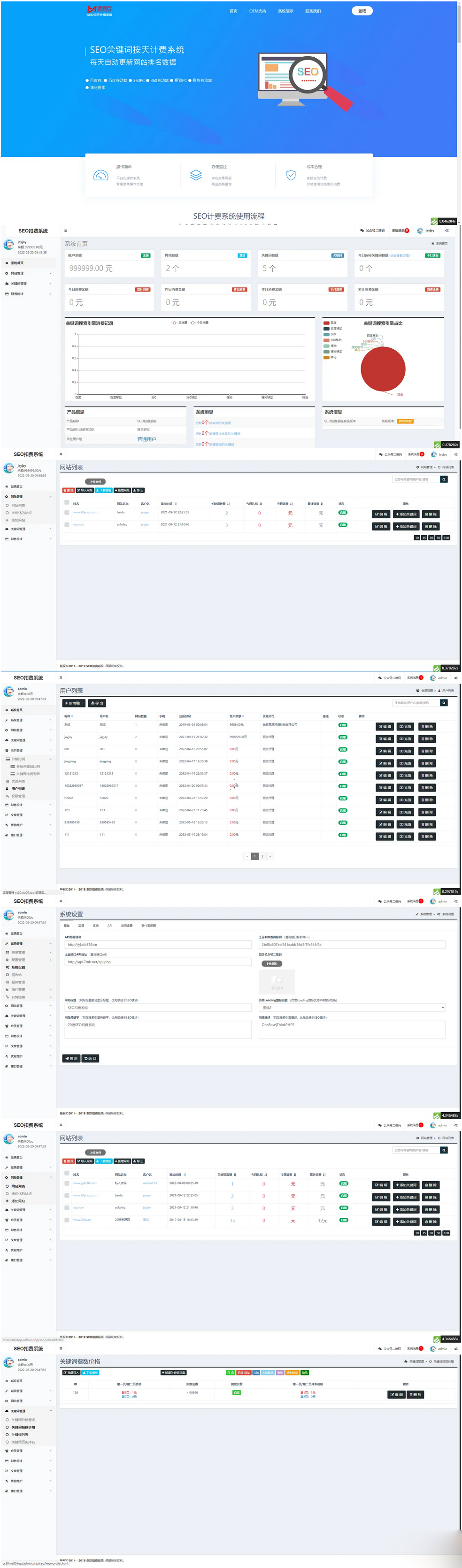
(带教程)商业版SEO关键词按天计费系统:关键词排名优化、代理服务、手机自适应及搭建教程
源码简介: 1、会员管理: 该系统分为三个级别的会员流程:总站管理员、代理与会员(会员有普通会员、中级会员和高级会员三个等级)。总站管理员可以添加代理用户并为其充值余额,代理用户可以为普通用户充值余…...
IDEA 快捷键汇总
目录 1、altinsert 2、ctrl/ 3、altenter 4、alt回车 5、ctrlD 6、ctrlaltL 7、ctrl点击 8、alt左键向下拉 9、ctrlaltv 10、ctrlaltwint 1、altinsert 快速创建代码,可以快速创建类中get set tostring等方法 2、ctrl/ 单行注释 3、altenter…...

目标检测YOLO实战应用案例100讲-基于机器视觉的水稻病虫害监测预警
目录 前言 国内外研究现状 国外研究现状 国内研究现状 2 相关理论与技术...

OrthoNets:正交信道注意网络
文章目录 摘要1、简介2、相关工作3、方法4、实验设置及结果5、论述6、结论摘要 链接:https://arxiv.org/pdf/2311.03071v2.pdf 设计有效的通道注意力机制要求人们找到一种有损压缩方法,以实现最佳特征表示。尽管该领域近年来取得了进展,但仍然存在一个未解决的问题。FcaNet…...
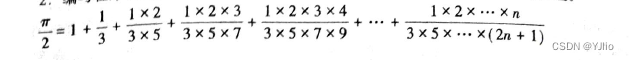
C_12练习题
一、单项选择题(本大题共20小题,每小题2分,共40分。在每小题给出的四个备选项中,选出一个正确的答案,并将所选项前的字母填写在答题纸的相应位置上。) C 风格的注释,也称块注释或多行注释,以()…...

导航守卫有哪三种?
导航守卫主要分为三种: 全局前置守卫:使用 router.beforeEach 注册,作用是在路由切换开始前进行拦截和处理,可以用来进行一些全局的权限校验、登录状态检查等操作。 全局解析守卫:使用 beforeResolve 注册,…...

强烈 推荐 13 个 Web前端在线代码IDE
codesandbox.io(国外,提供免费空间) 网址:https://codesandbox.io/ CodeSandbox 专注于构建完整的 Web 应用程序,支持多种流行的前端框架和库,例如 React、Vue 和 Angular。它提供了一系列增强的功能&…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

欢乐熊大话蓝牙知识17:多连接 BLE 怎么设计服务不会乱?分层思维来救场!
多连接 BLE 怎么设计服务不会乱?分层思维来救场! 作者按: 你是不是也遇到过 BLE 多连接时,调试现场像网吧“掉线风暴”? 温度传感器连上了,心率带丢了;一边 OTA 更新,一边通知卡壳。…...

AI书签管理工具开发全记录(十八):书签导入导出
文章目录 AI书签管理工具开发全记录(十八):书签导入导出1.前言 📝2.书签结构分析 📖3.书签示例 📑4.书签文件结构定义描述 🔣4.1. 整体文档结构4.2. 核心元素类型4.3. 层级关系4.…...
