记录一些涉及到界的题
文章目录
- coppersmith的一些相关知识
- 题1 [N1CTF 2023] e2W@rmup
- 题2 [ACTF 2023] midRSA
- 题3 [qsnctf 2023]
- 浅记一下
coppersmith的一些相关知识
上界 X = c e i l ( 1 2 ∗ N β 2 d − ϵ ) X = ceil(\frac{1}{2} * N^{\frac{\beta^2}{d} - \epsilon}) X=ceil(21∗Ndβ2−ϵ) (向上取整)
分别对应于coppersmith中small_roots(X,beta,espilon)的各个参数
官方文档

X:所求根的上界
beta ( β ) (\beta) (β):限定因子,满足 b > = N β b >= N^{\beta} b>=Nβ,默认值为1 (所以此情况下b = N)。
(找到 f(x) = 0 的一个解,使它在模 n 的某个因子时成立,此时这里说的某个因子即为b,在rsa中n = p * q,只有两个因子,故此时的b即p或q。一般我们遇到的题中p,q位数都是相等的,故beta可取0.5,但更多情况下我们并不知道p,q哪个大,所以保险起见beta通常取0.4) (可以取两位小数吗,有待存疑,得去验证一下。)
epsilon ( ϵ ) (\epsilon) (ϵ):限定因子,默认值为 β / 8 \beta / 8 β/8 = 1/8 = 0.1
d:f(x)的度,高位攻击中d = 1
在方程F(x),模数N确认的情况下,我们可以通过增加 β \beta β 的取值或减小 ϵ \epsilon ϵ 的取值,使得X取到更优的上界。
测试后发现是可以取两位小数的 (虽然官方文档中是一位小数)
并且可以得到以下结论:
p,q 512bit ---- 未知227bit , coppersmith定理可求解 (0.38 <= beta <= 0.44)
p,q 512bit ---- 未知248bit , coppersmith定理可求解 (0.40 <= beta <= 0.49, epsilon = 0.01)
p,q 512bit ---- 未知250bit , coppersmith定理可求解 (beta = 0.5, epsilon = 0.01 , p进行求解且p > q)
p,q1024bit — 未知554bit , coppersmith定理可求解 (0.38 <= beta <= 0.44)
p,q1024bit — 未知496bit , coppersmith定理可求解 (0.40 <= beta <= 0.49, epsilon = 0.01)
p,q1024bit ----未知500bit , coppersmith定理可求解 (beta = 0.5, epsilon = 0.01 , p进行求解且p > q)
(好巧不巧,正好两倍关系,很好的一个结果)
但其实可以发现得到的结果和最上面的公式并不是我们以为的一对一关系,公式只是给我们一个大概值,要得到最终的实际结果更多的是靠我们自己去调beta和epsilon
题1 [N1CTF 2023] e2W@rmup
题目描述:
import hashlib
import ecdsa
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from Crypto.Util.number import *
from secret import flagdef gen():curve = ecdsa.NIST256p.generatororder = curve.order()d = randint(1, order-1)while d.bit_length() != 256:d = randint(1, order-1)pubkey = ecdsa.ecdsa.Public_key(curve, curve * d)privkey = ecdsa.ecdsa.Private_key(pubkey, d)return pubkey, privkey, ddef nonce_gen(msg, d):msg_bin = bin(msg)[2:].zfill(256)d_bin = bin(d)[2:].zfill(256)nonce = int(msg_bin[:128] + d_bin[:128], 2)return noncedef sign(msg, privkey, d):msg_hash = bytes_to_long(hashlib.sha256(msg).digest())nonce = nonce_gen(msg_hash, d)sig = privkey.sign(msg_hash, nonce)s, r = sig.s, sig.rreturn s, rpk, sk, d = gen()
msg = b'welcome to n1ctf2023!'
s, r = sign(msg, sk, d)
print(f's = {s}')
print(f'r = {r}')m = pad(flag, 16)
aes = AES.new(long_to_bytes(d), mode=AES.MODE_ECB)
cipher = aes.encrypt(m)
print(f'cipher = {cipher}')"""
s = 98064531907276862129345013436610988187051831712632166876574510656675679745081
r = 9821122129422509893435671316433203251343263825232865092134497361752993786340
cipher = b'\xf3#\xff\x17\xdf\xbb\xc0\xc6v\x1bg\xc7\x8a6\xf2\xdf~\x12\xd8]\xc5\x02Ot\x99\x9f\xf7\xf3\x98\xbc\x045\x08\xfb\xce1@e\xbcg[I\xd1\xbf\xf8\xea\n-'
"""
题目分析:
s = ( h ( m ) + d ∗ r ) ∗ k − 1 d = d h ∗ 2 128 + d l d ( m ) = m h ∗ 2 128 + m l k = m h ∗ 2 128 + d h ⇒ s = ( h ( m ) + ( d h ∗ 2 128 + d l ) ∗ r ) ∗ ( m h ∗ 2 128 + d h ) − 1 ⇒ d l = ( s ∗ r − 1 − 2 128 ) ∗ d h + ( s ∗ m h ∗ 2 128 − h ( m ) ) ∗ r − 1 d l ≡ A ∗ d h + B m o d q 其 中 b i t s ( d l ) = b i t s ( d h ) = b i t s ( q ) / / 2 b i t s ( A ) = b i t s ( B ) = b i t s ( q ) s = (h(m) + d * r) * k^{-1}\\ d = d_h * 2 ^ {128} + d_l\\ d(m) = m_h * 2 ^ {128} + m_l\\ k = m_h * 2^{128} + d_h\\ \Rightarrow s = (h(m) + (d_h * 2^{128} + d_l)* r) * (m_h * 2 ^ {128} + d_h)^{-1}\\ \Rightarrow d_l = (s * r^{-1} - 2 ^{128}) * d_h + (s * m_h * 2 ^ {128} - h(m)) * r ^{-1}\\ d_l \equiv A * d_h + B \mod q\\ 其中bits(d_l) = bits(d_h) = bits(q) // 2\\ bits(A) = bits(B) = bits(q)\\ s=(h(m)+d∗r)∗k−1d=dh∗2128+dld(m)=mh∗2128+mlk=mh∗2128+dh⇒s=(h(m)+(dh∗2128+dl)∗r)∗(mh∗2128+dh)−1⇒dl=(s∗r−1−2128)∗dh+(s∗mh∗2128−h(m))∗r−1dl≡A∗dh+Bmodq其中bits(dl)=bits(dh)=bits(q)//2bits(A)=bits(B)=bits(q)
我开始是直接构造的,没得到想要的结果,可知是卡界了(所要求的目标向量超过了限度)
也可以通过高斯启发式判别
The Gaussian Heuristic 是对赫米特常数的进一步缩小定义:
L是n维格,高斯所期望的最短的长度是:
σ ( L ) = n 2 π e ( det L ) 1 / n \mathrm{\sigma(L)=\sqrt{\frac n{2\pi e}}~(\det L)^{1/n}} σ(L)=2πen (detL)1/n
高斯启发式表示,在一个“随机选择的格”中的最短非零向量满足
∣ ∣ ν shortest ∣ ∣ ≈ σ ( L ) ||\nu_\text{shortest }||\approx\sigma(\mathcal{L}) ∣∣νshortest ∣∣≈σ(L)
更精确地,假如确定了 ϵ > 0 \epsilon>0 ϵ>0,则当n足够大时的n维格L满足( 1 − ϵ ) σ ( L ) ≤ ∣ ∣ ν shortest ∣ ∣ ≤ ( 1 + ϵ ) σ ( L ) (1-\epsilon)\sigma(\mathrm{L})\leq||\nu_\text{shortest }||\leq(1+\epsilon)\sigma(\mathrm{L}) (1−ϵ)σ(L)≤∣∣νshortest ∣∣≤(1+ϵ)σ(L)
卡界了怎么办,可以通过爆破一位缩小目标向量,论文在此
x ∗ 2 127 + d l ′ ≡ A ∗ ( 1 ∗ 2 127 + d h ′ ) + B m o d q d l ′ ≡ A ∗ d h ′ + ( B + ( A − x ) ∗ 2 127 ) d l ′ ≡ A ∗ d h ′ + B B , 构 造 如 下 : ( q A 1 B B 2 127 ) x * 2^{127} + d_l' \equiv A * (1 * 2 ^{127} + d_h' ) + B \mod q\\ d_l' \equiv A * d_h' + (B + (A - x) * 2 ^{127})\\ d_l' \equiv A * d_h' + BB,构造如下:\\ \begin{pmatrix} q&&\\ A&1&\\ BB&&2^{127} \end{pmatrix} x∗2127+dl′≡A∗(1∗2127+dh′)+Bmodqdl′≡A∗dh′+(B+(A−x)∗2127)dl′≡A∗dh′+BB,构造如下:⎝⎛qABB12127⎠⎞
import hashlib
import ecdsa
from Crypto.Util.number import *
from gmpy2 import *
from Crypto.Cipher import AES
curve = ecdsa.NIST256p.generator
q = curve.order()
a=ecdsa.NIST256p.curve.a()
b=ecdsa.NIST256p.curve.b()
p=ecdsa.NIST256p.curve.p()
msg = b'welcome to n1ctf2023!'
msg_hash = bytes_to_long(hashlib.sha256(msg).digest())s = 98064531907276862129345013436610988187051831712632166876574510656675679745081
r = 9821122129422509893435671316433203251343263825232865092134497361752993786340
cipher = b'\xf3#\xff\x17\xdf\xbb\xc0\xc6v\x1bg\xc7\x8a6\xf2\xdf~\x12\xd8]\xc5\x02Ot\x99\x9f\xf7\xf3\x98\xbc\x045\x08\xfb\xce1@e\xbcg[I\xd1\xbf\xf8\xea\n-'y = 1 << 127
x = 1 << 127
A = (s * inverse(r,q) - 2 ** 128) % q
B = (s * (msg_hash // 2 ** 128) * 2 ** 128 - msg_hash) * inverse(r,q) % qBB = ((A * y - x) + B) % qM = matrix(ZZ,[[q,0,0],[A,1,0],[BB,0,2 ** 127]])L = M.LLL()[0]
d = (L[1] + y) * 2 ** 128 + L[0] + x
aes = AES.new(long_to_bytes(d), mode=AES.MODE_ECB)
print(aes.decrypt(cipher))
题2 [ACTF 2023] midRSA
题目描述:
from secret import flag
from Crypto.Util.number import *def genKey(nbits, dbits):bbits = (nbits // 2 - dbits) // 2while True:a = getRandomNBitInteger(dbits)b = getRandomNBitInteger(bbits)c = getRandomNBitInteger(bbits)p1 = a * b * c + 1if isPrime(p1):# print("p1 =", p1)breakwhile True:d = getRandomNBitInteger(dbits)p2 = b * c * d + 1if isPrime(p2):# print("p2 =", p2)breakwhile True:e = getRandomNBitInteger(bbits)f = getRandomNBitInteger(bbits)q1 = e * d * f + 1p3 = a * e * f + 1if isPrime(q1) and isPrime(p3):# print("p3 =", p3)# print("q1 =", q1)breakwhile True:d_ = getRandomNBitInteger(dbits)if GCD(a * b * c * d * e * f, d_) != 1:continuee_ = inverse(d_, a * b * c * d * e * f)k1 = (e_ * d_ - 1) // (a * b * c * d * e * f)assert e_ * d_ == (a * b * c * d * e * f) * k1 + 1q2 = k1 * e * f + 1q3 = k1 * b * c + 1if isPrime(q2) and isPrime(q3):# print("q2 =", q2)# print("q3 =", q3)# print("e =", e_)print("d =", d_)breakn1 = p1 * q1n2 = p2 * q2n3 = p3 * q3assert pow(pow(0xdeadbeef, e_, n1), d_, n1) == 0xdeadbeefassert pow(pow(0xdeadbeef, e_, n2), d_, n2) == 0xdeadbeefassert pow(pow(0xdeadbeef, e_, n3), d_, n3) == 0xdeadbeefreturn(e_, n1, n2, n3)nbits = 0x600
dbits = 0x240m = bytes_to_long(flag)
e, n1, n2, n3 = genKey(nbits, dbits)
c = pow(m, e, n1)print("c =", c)
print("e =", e)
print("n1 =", n1)
print("n2 =", n2)
print("n3 =", n3)# c = 598823083137858565473505718525815255620672892612784824187302545127574115000325539999824374357957135208478070797113625659118825530731575573239221853507638809719397849963861367352055486212696958923800593172417262351719477530809870735637329898331854130533160020420263724619225174940214193740379571953951059401685115164634005411478583529751890781498407518739069969017597521632392997743956791839564573371955246955738575593780508817401390102856295102225132502636316844
# e = 334726528702628887205076146544909357751287869200972341824248480332256143541098971600873722567713812425364296038771650383962046800505086167635487091757206238206029361844181642521606953049529231154613145553220809927001722518303114599682529196697410089598230645579658906203453435640824934159645602447676974027474924465177723434855318446073578465621382859962701578350462059764095163424218813852195709023435581237538699769359084386399099644884006684995755938605201771
# n1 = 621786427956510577894657745225233425730501124908354697121702414978035232119311662357181409283130180887720760732555757426221953950475736078765267856308595870951635246720750862259255389006679454647170476427262240270915881126875224574474706572728931213060252787326765271752969318854360970801540289807965575654629288558728966771231501959974533484678236051025940684114262451777094234017210230731492336480895879764397821363102224085859281971513276968559080593778873231
# n2 = 335133378611627373902246132362791381335635839627660359611198202073307340179794138179041524058800936207811546752188713855950891460382258433727589232119735602364790267515558352318957355100518427499530387075144776790492766973547088838586041648900788325902589777445641895775357091753360428198189998860317775077739054298868885308909495601041757108114540069950359802851809227248145281594107487276003206931533768902437356652676341735882783415106786497390475670647453821
# n3 = 220290953009399899705676642623181513318918775662713704923101352853965768389363281894663344270979715555659079125651553079702318700200824118622766698792556506368153467944348604006011828780474050012010677204862020009069971864222175380878120025727369117819196954091417740367068284457817961773989542151049465711430065838517386380261817772422927774945414543880659243592749932727798690742051285364898081188510009069286094647222933710799481899960520270189522155672272451
题目分析:
E ∗ D − k 1 ∗ n 1 = x E ∗ D − a ∗ n 2 = y E ∗ D − d ∗ n 3 = z a , d , k 1 , D − − d b i t s x , y , z − − n b i t s / / 2 + d b i t s E , n 1 , n 2 , n 3 − − n b i t s 一 开 始 会 想 到 构 造 如 下 : ( − k 1 , − a , − d , D ) ( n 1 n 2 n 3 E E E 2 768 ) = ( x , y , z , D ∗ 2 768 ) E * D - k_1 * n_1 = x\\ E * D - a * n_2 = y\\ E * D - d * n_3 = z\\ a,d,k_1,D -- dbits\\ x,y,z -- nbits//2 + dbits\\ E,n_1,n_2,n_3 -- nbits\\ 一开始会想到构造如下:\\ (-k_1,-a,-d,D)\begin{pmatrix} n_1&&&\\ &n_2&&\\ &&n_3&\\ E&E&E&2^{768} \end{pmatrix} = (x,y,z,D * 2^{768}) E∗D−k1∗n1=xE∗D−a∗n2=yE∗D−d∗n3=za,d,k1,D−−dbitsx,y,z−−nbits//2+dbitsE,n1,n2,n3−−nbits一开始会想到构造如下:(−k1,−a,−d,D)⎝⎜⎜⎛n1En2En3E2768⎠⎟⎟⎞=(x,y,z,D∗2768)
不过又没得到想要的结果,但长度相近,可以想到又是卡界了
用上面所构造的格测试后知道D位数最多573位,但这里577位,多了4位
这里使用爆破法,爆破D的前16位来扩大格的界(爆破14位能出,不过我这是提前知道了结果)
E ∗ ( D h ∗ 2 16 + D l ) − k 1 ∗ n 1 = x E ∗ 2 16 ∗ D h + E ∗ D l − k 1 ∗ n 1 = x E ∗ 2 16 ∗ D h + E ∗ D l − a ∗ n 2 = y E ∗ 2 16 ∗ D h + E ∗ D l − d ∗ n 3 = z 构 造 如 下 格 : ( 2 16 + d b i t s E 2 16 E 2 16 E 2 16 0 0 n 1 0 0 0 0 0 n 2 0 0 0 0 0 n 3 0 0 E D l E D l E D l 2 n b i t s / / 2 + d b i t s ) E * (D_h * 2 ^ {16} + D_l) - k_1 * n_1 = x\\ E * 2 ^ {16} * D_h + E * D_l - k_1 * n_1 = x\\ E * 2 ^ {16} * D_h + E * D_l - a * n_2 = y\\ E * 2 ^ {16} * D_h + E * D_l - d* n_3 = z\\ 构造如下格:\\ \begin{pmatrix} 2^{16 + dbits}&E2 ^ {16}&E2 ^ {16}&E2 ^ {16}&0\\ 0&n_1&0&0&0\\ 0&0&n_2&0&0\\ 0&0&0&n_3&0\\ 0& ED_l & ED_l &ED_l &2^{nbits//2 + dbits} \end{pmatrix} E∗(Dh∗216+Dl)−k1∗n1=xE∗216∗Dh+E∗Dl−k1∗n1=xE∗216∗Dh+E∗Dl−a∗n2=yE∗216∗Dh+E∗Dl−d∗n3=z构造如下格:⎝⎜⎜⎜⎜⎛216+dbits0000E216n100EDlE2160n20EDlE21600n3EDl00002nbits//2+dbits⎠⎟⎟⎟⎟⎞
from Crypto.Util.number import *
from tqdm import tqdmc = 598823083137858565473505718525815255620672892612784824187302545127574115000325539999824374357957135208478070797113625659118825530731575573239221853507638809719397849963861367352055486212696958923800593172417262351719477530809870735637329898331854130533160020420263724619225174940214193740379571953951059401685115164634005411478583529751890781498407518739069969017597521632392997743956791839564573371955246955738575593780508817401390102856295102225132502636316844
e = 334726528702628887205076146544909357751287869200972341824248480332256143541098971600873722567713812425364296038771650383962046800505086167635487091757206238206029361844181642521606953049529231154613145553220809927001722518303114599682529196697410089598230645579658906203453435640824934159645602447676974027474924465177723434855318446073578465621382859962701578350462059764095163424218813852195709023435581237538699769359084386399099644884006684995755938605201771
n1 = 621786427956510577894657745225233425730501124908354697121702414978035232119311662357181409283130180887720760732555757426221953950475736078765267856308595870951635246720750862259255389006679454647170476427262240270915881126875224574474706572728931213060252787326765271752969318854360970801540289807965575654629288558728966771231501959974533484678236051025940684114262451777094234017210230731492336480895879764397821363102224085859281971513276968559080593778873231
n2 = 335133378611627373902246132362791381335635839627660359611198202073307340179794138179041524058800936207811546752188713855950891460382258433727589232119735602364790267515558352318957355100518427499530387075144776790492766973547088838586041648900788325902589777445641895775357091753360428198189998860317775077739054298868885308909495601041757108114540069950359802851809227248145281594107487276003206931533768902437356652676341735882783415106786497390475670647453821
n3 = 220290953009399899705676642623181513318918775662713704923101352853965768389363281894663344270979715555659079125651553079702318700200824118622766698792556506368153467944348604006011828780474050012010677204862020009069971864222175380878120025727369117819196954091417740367068284457817961773989542151049465711430065838517386380261817772422927774945414543880659243592749932727798690742051285364898081188510009069286094647222933710799481899960520270189522155672272451
for dl in tqdm(range(2 ** 14)):edl = e * dlM = Matrix(ZZ,[[2 ^ (14 + 768),e * 2 ^ 14,e * 2 ^ 14,e * 2 ^ 14,0],[0,-n1,0,0,0],[0,0,-n2,0,0],[0,0,0,-n3,0],[0,edl,edl,edl,2 ^ (576 + 768)]])L = M.LLL()[0]if abs(L[-1]) != 2 ^ (576 + 768): continued=abs(L[0]//2^768) + dlm = long_to_bytes(ZZ(pow(c,d,n1)))if b'ACTF' in m:print(m,i)break#ACTF{5FFC427B-F14F-DCA0-C425-675B149890C2}
一开始是只爆破4位,没出,想了一下4位要均分到5行里面,每行分一位都分不到,所以不行,得多爆几位,最起码得10位吧,10位不行那就继续往上加,再加4位这就行了
题3 [qsnctf 2023]
题目描述:
from Crypto.Util.number import *
from secrets import flag, x, y, z
from sympy.ntheory import prevprime
from Crypto.Cipher import AES
from Crypto.Util.Padding import padRound = 32
q = 2 ** 256
for i in [x,y,z]:assert i.bit_length() == 256A = []
B = []
for i in range(Round):a = getRandomInteger(256)A.append(a)b = (a * x % q) >> (256 - 8)B.append(b)
print(A)
print(B)
'''
[3561678147813669042672186969104055553515262226168087322052560790885260761433, 17346407693442644010055116546363960164095133759884497841925887458500171929994, 10970839811545507511408260800883769581649579684426188079142754412064502787585, 109417222922540235139013912297145185193443712852193270682885305502867182588403, 88171850234002600580608014259219586239590114856448092326801813245774395730496, 5113619435362108938262679062561727235116615800676783173565082653599747645155, 54576089683044230333058389148818602636893918880220233916359714009830588044131, 46319652232696496987147414399965164805770427009639155019904825551069668519260, 92142202700489403870481152403139465532735056770434774464930082474517829581964, 9084526539780165183228300902059842905058839285187659313361650962576085292818, 89120115360204223476154240731792191817638074392691790750005020564226279037550, 108874944765319253896194176909539011617418473448207058050594223215460183828033, 48697630410338199345605370644643425030874923782845194702123578264330641464094, 90490831141215467713642375752174358047945797806394912036159392371419919773636, 5407847525945777533863763148921176292074562577253075889320641646783216244238, 95326999116234880776873896438659550308182265903511015349887289749187746932743, 13848646478536701368088661040908693291788138011605835864557858216170511016083, 12688154545015600072136788151484672710661959298941783293908174000377900727747, 103416430654164637952330806792686485956010294787748757584715063906414248209722, 36213989454986448247979083323211284869162879484215027121399406834805531673463, 83477199408920970502661396196378764693640078246444907844363833717275362253336, 54685544287120130615023910691215446521783587675140445694155062634358785975223, 57209914633582227771666953772776413914105217956486621477363100169491699389485, 60722705656546434007907580733214759241271810206392571495455413850603913610651, 62666312072142619643565102615355724228875566515181602729719018682721112131326, 17892029370519322177254795109531838575579273633357811419566887056272012019617, 23387537005911727415991488713130020055341902697712259630978747015670850612866, 57084096974333718635810536400151484653413307540676932220675888461543384910791, 64672020284448913361212245534680048800817888816777270292913433441383929287826, 30879668079119218442051482226185849538064516289533962210948424807374221747937, 67805294126621083377517953883639091568886644480832055617022550683600509359637, 80971248361778969534551851802629859076303703583702628504189145200772632698437]
[185, 121, 74, 192, 66, 208, 189, 5, 248, 216, 222, 49, 199, 122, 212, 109, 36, 135, 9, 43, 94, 192, 67, 176, 165, 34, 241, 27, 255, 216, 71, 156]
'''
q = prevprime(q)
print(q)
A = []
B = []
for i in range(Round+1):a = getRandomInteger(256)A.append(a)b = (a * y % q) & (2 ** 8 - 1)B.append(b)
print(A)
print(B)
'''
115792089237316195423570985008687907853269984665640564039457584007913129639747
[46504565744057869379592149118750005180204315285587793650459698458291497313095, 58007957093934046182693035826219870499452741234326847327688846747059237094075, 50185124619087453830679170251457196445767905313509337058697814870412730362947, 13460057838246434192804076595664204927155595158673092664009965681276162112064, 1701081975560116286696366369808334022446618430663926380667987754925635360535, 26884871731419084105623632272724863769910293366201375037286643905133449526668, 86148369125917615329995354501659454507150263427394081644953922899405044908942, 86965847264933041291798488655625963084424620038983026175910367027955449692128, 51359332101276868450990110421905601457823984827989287103931757850844231666586, 48796757902016638482644909388959646721244669665114474829651238484065619118952, 100070448202859232758452766870542683109402601193511866026529530855112793822109, 96580256984898125874774601478072811945116066886633284314860596683569097605765, 38808894076998102467847013020946201384521577320197543440467015636483307894892, 4134554141092625841029701614640247691101835437566908306546904884177729072687, 74873085435488619613395208820994521773265984299598688734149106712561237976724, 15654842239708870234259249156913701671624803564647865424705391694462101457862, 88322093034453332197643606249439750127876581478584569790806716889277489637972, 22499556277754006237442593359493863007223009260764163505327306701416065559119, 67089035688878297307085968283413144678391442218184879365509351597884743967932, 27674630243557284124557851587722479960748242794492773619925160133318279977692, 9119521864491019262790789925266797995577993021425216600126182732190292182948, 101288882073195598657612116292233377922026161322404160341330451374348438098216, 67804446744028818432860934046262550895247933787912806120088242004054790700495, 26086948144209799352019678059923693118044934151861294461002114985645656470189, 38144657569843600236424138168852321656171547769351620499893335164030638528328, 29607623036881080673594862278805535156351844098214001235565521439825687173709, 73322408962909922161031457562287596779866102699954700495813418822123077110802, 71841446787131237842866428647552570448973984694577468650052516966413175250298, 1230436323839997562475731649322922330998915952913300933165504728647309839568, 107223013661981482036189531938571461516528131559156846625598018135279924645933, 40439925178577390217639900040814034803597438472158408491211685077053585300286, 26978587850306490903937574562860250724695533954879823140348556476663322417613, 82195886203427304567763311291077205482622324404366375181470500496565215770146]
[115, 240, 228, 198, 160, 178, 214, 160, 96, 140, 89, 186, 159, 102, 192, 93, 135, 30, 17, 9, 138, 224, 109, 116, 76, 116, 180, 196, 121, 187, 210, 208, 14]
'''q = 2**256
A = []
B = []
for i in range(103):a = getRandomInteger(256)A.append(a)b = (a * z % q) >> (256 - 4)B.append(b)
print(A)
print(B)
'''
[56666422659665306957613341966104139188430887040369382699811066965734652038579, 41608423494025514337106193470276163502869431432921281068110444274310186909892, 95312645577996377489331859379729367791539181995403307071242251663306260824059, 114007089082826788908311397311915638668862713690403097281136795912671634293903, 77470602549297888428039543840134276433567854766634294661906479236200644990851, 67265570384781545307301479187933437206481537999752352862466291209724038113997, 101015220564168271842813302532972922828562060680762307341661161853013181455988, 73596220918173964622453801478597395507613363519777836354319778006747628725943, 80276240092293162850897330969848557221924558822619435206166856373482558821153, 60387041856575123107349887176488814324533329129026453912394888320971261329267, 37588667650535221417005569007639921039223353621264869144904381190769978830432, 30201673227033963823582196954697293400001560479877858941307825349312312395908, 46517796724693810353256110303591718873843585558937781709113232176049614134229, 110476911183528409932385631377040635032167229294859921626233104995069707326026, 33913880276956766352570275848477001195330941450588079882929631222080051897977, 108738411950576541236703456832793461013595057668683247592686862598082364613770, 87211442745029489881514515811064102429019356351722823450170249465088775249507, 39600946693670273230261533720839589755726946308581706825676138619972092199256, 4979886914346369664911891403751631037886315717549974065878536283157637402320, 22272529908653383795002294860870129574984518813560375272257703512940569602004, 100135751785995415247695765442899140606914076750888419237400306294448451415863, 85613534858376605408667291532701284666560850915689941354202786014968649139457, 38496246133430733988750968353732662162312705079114417415163071485082991344590, 55980481790171446152748793757788577465044360548729573345122559743628093363153, 71280277172994137969689292719624075379102489317199533126561191722460505314026, 110446223482446943024326135434573497276437669060614612856002207641927747194266, 16456085922385532110267651711339329146652084370610067373716816178321924748791, 101653629730678493695114228522885120593522618541788967122785214737946157867999, 74467527492811608068163160348674720595757862332879609098404557441577413104820, 41884843126443673947662657085537596879702074001592844509379139860812151553968, 29815687077578101251522932333124915023192910276895021601688368611558697857638, 44840628789800333625015337751638405696233468515566263356197320268202190223769, 102427595787595418722722430130631701884337456325150921017413824991597185452849, 2975107125099035075044003816426206055437890428466365543585422202932381886186, 94699511483779321185024950255977801474453881858185354369860946591141828290326, 31810607567540037649472765223870019465281477418301020106850480432511306591757, 75713781109794200255529510371465092460190607870508383754795316160075282283862, 55429849762380955520557448208384572772400405309708977900727750338226215580736, 71351843550447097631722656769410630908972124288367169285559142896305583201390, 84145371680533342029399999651802676680665442500082991947093355443249540103162, 18059328520840928370924328960454198116073475240703647573736616851363995779497, 83839387396741626377342400188482404639827411621171844172874897800772466334269, 25788978353065311499638204532308969267343091396798096623404684254370926606489, 46416171203559401945669998573205329748734005210989064607057470628982156110053, 42839223735347899899704913105525407073907314464785013094063759450820513757342, 88826657766811054515837039931572449230721258604658317309512814974116100196733, 53796508595019468595537500010909399217450133587528313928622717009905225347437, 56531378551320964008977461547054273860909442858252049481923559030063639435057, 48217679285988263588226655808041000825638438349841115697751615792350031644869, 64424297190010710116212288045994884168253983939992794298642423963632550451160, 46474911280506479688705284230861217499981118516937627597481370505066926962182, 64032029526907010327735757773865326038078238679652707012855320952596919166618, 5529383900219431454017233184818428510888383480088262580036064976358985800985, 69322608357555546086372761692837205200171798855109065251575534608627560525776, 76098979682650954216202311601813089916970156784884278240596741668163729505020, 91674126062289237651839995587104059408995800143522837051179562018281051100557, 90571390404208688843585603192800843878382529323359914123528861146103857760661, 72012664155317843790423022518639753138262519729890141457716216773019826138388, 66863180243825712563555363518892364864799935770917594234609418534062748300787, 5838945753982677965177087293687053018953448675487050703226841119623778529018, 4440280122867898274880560103713163505203269339591832639427292037957483435863, 113585052040012311817152621651926546174704034369418207806360593735979071392560, 96503008028224334771028807273628056037391407459560685791940303889130903300826, 67050454088005224845748627326789053425990922831763041158174139321910165797537, 56354656300386637831392267891729486882144501924180334206591055551662859511145, 108875538744684454340615686969559999736352047181969993978724550037003168200211, 105856150301241056513738964497224079598648612469774416566110150235952602587129, 103072133631485922917570773603973545510240103328265914435430955113182187850847, 105071449786380370702657927006338895312230491406739601631939501577997184496876, 101559564666645844079948496433098525970583827093303201782110972272082979410831, 45696832977481706385123240351386677526237953026854755659089774125668886575190, 92930863035601609905246064160817660898443604755800516139761871009073979122573, 7136157467487063026530735850363136522687472196852313490264738121297870888865, 62220552837071854508303645903133799707167271140998125870619424819338409845248, 71964156627499707284955744986659480338185350890617779236004729406075442337650, 56432954135882530785013240455908855171502152827770214700998108134515682426307, 24818258540494883741910232014072726664585493319546426193565346084848631309292, 68946604449180849807706382163388201284725162066731407078323925073762784383918, 78305860067531640486978712479618549593532447916095131216323237767823095149213, 40019412274222034245452650116905171509558126077504657023971877193155638952620, 6226049816877252622825028481234412013581804081798123571329306780957341285518, 72008834916679466207298598830558721788070004796890262626592503036925690499953, 24120184417962346330989331701326680837413020607663960631051474032512470756250, 106358126840983882959473879360172954895361540456426525458062716824086971706859, 96125062326106069117227627865988038851006615609777159985287487409738006940292, 33054514553432552301350757403482219452773112411443533998213496297361397155535, 41581969631676286214097564630767898944747546622643163224140263014954932195321, 22904365609725269502635057676962583581851475921482302591306344959978794545764, 64290237869656947632842147827818163107378784367086448814380499121557877108860, 30680084243764095315357070546550118749025091482163732007754607769361116153541, 13691292022145271355849518605344621718116294468846185203111794890637243685470, 25132284761110457596793743234989234799586919369754843892751414241493192284491, 12389505381820778753642609476404562621082110924974170017133920070419933455780, 71535924312884292159182314202796515340797288002505186265430063222078901533504, 12742977582401193716850400144097310370558409977576217736024733304490605337769, 75139886864475235332970108571588085544527733256425836467715638485512421268158, 106812400623906721014312287501764424395430875573845869345085033374152396156108, 91345106193584221920864389152087560188260652160092982315871571692181571481755, 65785148879985691725045496265911886841068140761050563941336015575029243383380, 1452703135528066004669796386925101704795733053841911703671961494738444465175, 44818107645190027629062089844645267760294751459286511227307352668787518517867, 26767624780451051554599928370950639364780468287039403780345758419855142782301, 73520682616655688427241752929498638616275480985470608873569998909405046919540]
[11, 14, 12, 1, 13, 15, 1, 14, 12, 12, 15, 6, 2, 15, 13, 15, 6, 6, 11, 12, 2, 9, 3, 15, 0, 14, 10, 10, 13, 10, 6, 13, 6, 9, 0, 4, 9, 0, 15, 5, 2, 13, 12, 12, 5, 11, 3, 3, 12, 13, 5, 5, 14, 15, 12, 10, 9, 6, 8, 5, 8, 4, 12, 1, 15, 1, 14, 11, 11, 14, 6, 10, 6, 3, 14, 10, 10, 14, 5, 15, 6, 4, 13, 1, 5, 4, 7, 4, 13, 7, 0, 14, 6, 7, 2, 14, 1, 14, 6, 9, 14, 4, 13]
'''
# enc
key = x ^ y ^ z
key = long_to_bytes(key)
aes = AES.new(key,mode = AES.MODE_ECB)
print(aes.encrypt(pad(flag,16)))
# b'\xda\xfc\xb7\x93\xfb\x9d\xbe\x82\xb3\xb5\x87`]}\x0b*\xd53AR\x8bb\xfeQ,\xd9\xff\xf6\n\xa2\x1b)H\\\xf24>E\xac+\x01\xf3)F\x8c\xee\xb8j\x18zb\xa8\x8b\xba\xbc\xbb\x03\xbb}\xb6\x8cO#\xeb\x0c\xce\xbd\x07\x8aWP\x90\xf2\xaep\x02\x11{\xdf\xc5'
part1:
泄露高8位
b h ∗ 2 248 + b l ≡ a ∗ x b l = a ∗ x − b h ∗ 2 248 + k ∗ q 一 开 始 本 来 是 构 造 下 面 这 种 ( b h 后 ∗ 2 248 省 略 了 ) : ( l 1 , l 2 , . . . , x , − 1 ) ( q q ⋱ q a 1 a 2 ⋯ a 32 2 − 8 b h 1 b h 2 ⋯ b h 32 2 248 ) = ( b l 1 , b l 2 , . . . , x 2 − 8 , 2 248 ) b_h * 2^{248} + b_l \equiv a * x\\ b_l = a * x - b_h * 2^{248} + k * q\\ 一开始本来是构造下面这种(b_h后*2^{248}省略了):\\ (l_1,l_2,...,x,-1)\begin{pmatrix} q&&&&&\\ &q&&&&\\ &&\ddots&&&\\ &&&q\\ a_1&a_2&\cdots&a_{32}&2^{-8}\\ b_{h1}&b_{h2}&\cdots&b_{h32}&&2^{248}\end{pmatrix} = (b_{l1},b_{l2},...,x2^{-8},2^{248}) bh∗2248+bl≡a∗xbl=a∗x−bh∗2248+k∗q一开始本来是构造下面这种(bh后∗2248省略了):(l1,l2,...,x,−1)⎝⎜⎜⎜⎜⎜⎜⎛qa1bh1qa2bh2⋱⋯⋯qa32bh322−82248⎠⎟⎟⎟⎟⎟⎟⎞=(bl1,bl2,...,x2−8,2248)
不过没得到我们想要的目标向量,但结果的长度相近,又是卡界
测试了下,这种构造就算不卡界也得不到结果,所以这种构造有问题,得换一种构造方法
参考糖醋小鸡块师傅的解法orz
b h 1 ∗ 2 248 + b l 1 ≡ a 1 ∗ x b h i ∗ 2 248 + b l i ≡ a i ∗ x 联 立 消 x a i ∗ ( b h 1 ∗ 2 248 + b l 1 ) ≡ a 1 ∗ ( b h i ∗ 2 248 + b l i ) b l i ≡ a i ∗ a 1 − 1 ∗ b l 1 + ( a i ∗ a 1 − 1 ∗ b h 1 ∗ 2 248 − b h i ∗ 2 248 ) b l i ≡ A ∗ b l 1 + B m o d q 构 造 下 面 这 种 : ( l 1 , l 2 , . . . , b l 1 , 1 ) ( q q ⋱ q A 1 A 2 ⋯ A 31 1 B 1 B 2 ⋯ A 31 2 248 ) = ( b l 2 , b l 3 , . . . , b l 1 , 2 248 ) b_{h1} * 2^{248} + b_{l1} \equiv a_1 * x\\ b_{hi} * 2^{248} + b_{li} \equiv a_i * x\\ 联立消x\\ a_i * (b_{h1} * 2^{248} + b_{l1}) \equiv a_1 * (b_{hi} * 2^{248} + b_{li} )\\ b_{li} \equiv a_i * a_1^{-1}*b_{l1} + (a_i * a_1^{-1} * b_{h1} * 2^{248} - b_{hi} * 2^{248})\\ b_{li} \equiv A*b_{l1} +B \mod q\\构造下面这种:\\ (l_1,l_2,...,b_{l1},1)\begin{pmatrix} q&&&&&\\ &q&&&&\\ &&\ddots&&&\\ &&&q\\ A_1&A_2&\cdots&A_{31}&1\\ B_1&B_{2}&\cdots&A_{31}&&2^{248}\end{pmatrix} = (b_{l2},b_{l3},...,b_{l1},2^{248}) bh1∗2248+bl1≡a1∗xbhi∗2248+bli≡ai∗x联立消xai∗(bh1∗2248+bl1)≡a1∗(bhi∗2248+bli)bli≡ai∗a1−1∗bl1+(ai∗a1−1∗bh1∗2248−bhi∗2248)bli≡A∗bl1+Bmodq构造下面这种:(l1,l2,...,bl1,1)⎝⎜⎜⎜⎜⎜⎜⎛qA1B1qA2B2⋱⋯⋯qA31A3112248⎠⎟⎟⎟⎟⎟⎟⎞=(bl2,bl3,...,bl1,2248)
也没得到我们想要的目标向量,发现卡了2bit(即如果是(a * x % q) >> (256 - 10),那么以上这种构造能出结果)
所以这里尝试减小目标向量:
b i ≡ ( 2 248 ∗ b h i + 2 247 ) + ( b l i − 2 247 ) b_i \equiv (2^{248} * b_{hi} + 2^{247}) + (b_{li} - 2^{247}) bi≡(2248∗bhi+2247)+(bli−2247)
b l i − 2 247 b_{li} - 2^{247} bli−2247 是我们要得到的,这样目标向量中每一项小了1bit ,最后确实也得到了结果
(我测的是卡了2bit,这种方法降1bit就能出,疑惑。不纠结了,继续往下)
解题代码:
from gmpy2 import *
from Crypto.Util.number import *
q = 2**256
A = [3561678147813669042672186969104055553515262226168087322052560790885260761433, 17346407693442644010055116546363960164095133759884497841925887458500171929994, 10970839811545507511408260800883769581649579684426188079142754412064502787585, 109417222922540235139013912297145185193443712852193270682885305502867182588403, 88171850234002600580608014259219586239590114856448092326801813245774395730496, 5113619435362108938262679062561727235116615800676783173565082653599747645155, 54576089683044230333058389148818602636893918880220233916359714009830588044131, 46319652232696496987147414399965164805770427009639155019904825551069668519260, 92142202700489403870481152403139465532735056770434774464930082474517829581964, 9084526539780165183228300902059842905058839285187659313361650962576085292818, 89120115360204223476154240731792191817638074392691790750005020564226279037550, 108874944765319253896194176909539011617418473448207058050594223215460183828033, 48697630410338199345605370644643425030874923782845194702123578264330641464094, 90490831141215467713642375752174358047945797806394912036159392371419919773636, 5407847525945777533863763148921176292074562577253075889320641646783216244238, 95326999116234880776873896438659550308182265903511015349887289749187746932743, 13848646478536701368088661040908693291788138011605835864557858216170511016083, 12688154545015600072136788151484672710661959298941783293908174000377900727747, 103416430654164637952330806792686485956010294787748757584715063906414248209722, 36213989454986448247979083323211284869162879484215027121399406834805531673463, 83477199408920970502661396196378764693640078246444907844363833717275362253336, 54685544287120130615023910691215446521783587675140445694155062634358785975223, 57209914633582227771666953772776413914105217956486621477363100169491699389485, 60722705656546434007907580733214759241271810206392571495455413850603913610651, 62666312072142619643565102615355724228875566515181602729719018682721112131326, 17892029370519322177254795109531838575579273633357811419566887056272012019617, 23387537005911727415991488713130020055341902697712259630978747015670850612866, 57084096974333718635810536400151484653413307540676932220675888461543384910791, 64672020284448913361212245534680048800817888816777270292913433441383929287826, 30879668079119218442051482226185849538064516289533962210948424807374221747937, 67805294126621083377517953883639091568886644480832055617022550683600509359637, 80971248361778969534551851802629859076303703583702628504189145200772632698437]
B = [185, 121, 74, 192, 66, 208, 189, 5, 248, 216, 222, 49, 199, 122, 212, 109, 36, 135, 9, 43, 94, 192, 67, 176, 165, 34, 241, 27, 255, 216, 71, 156]AA = []
BB = []
invA = inverse(A[0],q)
for i in A[1:]:AA.append(i * invA % q)
for i in range(1,32):BB.append((A[i] * invA * (B[0] * 2**248 + 2 ** 247) - (B[i] * 2 ** 248 + 2 ** 247))% q)
M = Matrix(ZZ,33,33)
for i in range(31):M[i,i] = qM[-2,i] = AA[i]M[-1,i] = BB[i]M[-2,-2] = 1
M[-1,-1] = 2 ** 247
L = M.BKZ(block_size = 16)for i in L:if abs(i[-1]) == 2 ** 247:b = B[0] * 2 ** 248 - (i[-2]) + 2 ** 247 # 也可能是加号,加减自己测一下x = b * invA % qbb = []for i in range(32):# 核实if A[i] * x %q >> (256 - 8) != B[i]:breakif i == 31:print('res:',x)
# res: 80894527713686705071002739476859399489995408997139964746730066805048451766071
part2:
泄露低8位
一样的构造方法:
b i ≡ 2 8 ∗ b h i + b l i b i ≡ ( b h i ′ − 2 247 ) ∗ 2 8 + ( b l i + 2 255 ) ( m o d q ) b_i \equiv 2^{8} * b_{hi} + b_{li}\\ b_i \equiv (b_{hi}' - 2^{247} ) * 2^{8} + (b_{li} + 2^{255}) \pmod q bi≡28∗bhi+blibi≡(bhi′−2247)∗28+(bli+2255)(modq)
其中blocksize加到30能出结果(站在巨人的肩膀上写文,我这就直接说他的结果了)
解题代码:
from gmpy2 import *
from Crypto.Util.number import *
q = 115792089237316195423570985008687907853269984665640564039457584007913129639747
A = [46504565744057869379592149118750005180204315285587793650459698458291497313095, 58007957093934046182693035826219870499452741234326847327688846747059237094075, 50185124619087453830679170251457196445767905313509337058697814870412730362947, 13460057838246434192804076595664204927155595158673092664009965681276162112064, 1701081975560116286696366369808334022446618430663926380667987754925635360535, 26884871731419084105623632272724863769910293366201375037286643905133449526668, 86148369125917615329995354501659454507150263427394081644953922899405044908942, 86965847264933041291798488655625963084424620038983026175910367027955449692128, 51359332101276868450990110421905601457823984827989287103931757850844231666586, 48796757902016638482644909388959646721244669665114474829651238484065619118952, 100070448202859232758452766870542683109402601193511866026529530855112793822109, 96580256984898125874774601478072811945116066886633284314860596683569097605765, 38808894076998102467847013020946201384521577320197543440467015636483307894892, 4134554141092625841029701614640247691101835437566908306546904884177729072687, 74873085435488619613395208820994521773265984299598688734149106712561237976724, 15654842239708870234259249156913701671624803564647865424705391694462101457862, 88322093034453332197643606249439750127876581478584569790806716889277489637972, 22499556277754006237442593359493863007223009260764163505327306701416065559119, 67089035688878297307085968283413144678391442218184879365509351597884743967932, 27674630243557284124557851587722479960748242794492773619925160133318279977692, 9119521864491019262790789925266797995577993021425216600126182732190292182948, 101288882073195598657612116292233377922026161322404160341330451374348438098216, 67804446744028818432860934046262550895247933787912806120088242004054790700495, 26086948144209799352019678059923693118044934151861294461002114985645656470189, 38144657569843600236424138168852321656171547769351620499893335164030638528328, 29607623036881080673594862278805535156351844098214001235565521439825687173709, 73322408962909922161031457562287596779866102699954700495813418822123077110802, 71841446787131237842866428647552570448973984694577468650052516966413175250298, 1230436323839997562475731649322922330998915952913300933165504728647309839568, 107223013661981482036189531938571461516528131559156846625598018135279924645933, 40439925178577390217639900040814034803597438472158408491211685077053585300286, 26978587850306490903937574562860250724695533954879823140348556476663322417613, 82195886203427304567763311291077205482622324404366375181470500496565215770146]
B = [115, 240, 228, 198, 160, 178, 214, 160, 96, 140, 89, 186, 159, 102, 192, 93, 135, 30, 17, 9, 138, 224, 109, 116, 76, 116, 180, 196, 121, 187, 210, 208, 14]AA = []
BB = []
invA = inverse(A[0],q)
for i in A[1:]:AA.append(i * invA % q)
for i in range(1,33):BB.append((A[i] * invA * ((B[0] + 2 ** 255 ) * inverse(2**8,q)) - ((B[i] + 2 ** 255) * inverse(2**8,q)))% q)
M = Matrix(ZZ,34,34)
for i in range(32):M[i,i] = qM[-2,i] = AA[i]M[-1,i] = BB[i]M[-2,-2] = 1
M[-1,-1] = 2 ** 247
L = M.BKZ(block_size = 30)for i in L:if abs(i[-1]) == 2 ** 247:b = -(i[-2]) * 2 ** 8 + B[0] + 2 ** 255y = b * invA % qbb = []for i in range(32):# 核实if (A[i] * y % q) & (2 ** 8 - 1) != B[i]:breakif i == 31:print('res:',y)
# res: 98898469313641499500896146398219768802603949220366063599597841309427897612653
part3:
泄露高4位
和patr1一样的解法,blocksize加到22出结果 (直接报结果了)
解题代码:
from gmpy2 import *
from Crypto.Util.number import *
q = 2 ** 256
A= [56666422659665306957613341966104139188430887040369382699811066965734652038579, 41608423494025514337106193470276163502869431432921281068110444274310186909892, 95312645577996377489331859379729367791539181995403307071242251663306260824059, 114007089082826788908311397311915638668862713690403097281136795912671634293903, 77470602549297888428039543840134276433567854766634294661906479236200644990851, 67265570384781545307301479187933437206481537999752352862466291209724038113997, 101015220564168271842813302532972922828562060680762307341661161853013181455988, 73596220918173964622453801478597395507613363519777836354319778006747628725943, 80276240092293162850897330969848557221924558822619435206166856373482558821153, 60387041856575123107349887176488814324533329129026453912394888320971261329267, 37588667650535221417005569007639921039223353621264869144904381190769978830432, 30201673227033963823582196954697293400001560479877858941307825349312312395908, 46517796724693810353256110303591718873843585558937781709113232176049614134229, 110476911183528409932385631377040635032167229294859921626233104995069707326026, 33913880276956766352570275848477001195330941450588079882929631222080051897977, 108738411950576541236703456832793461013595057668683247592686862598082364613770, 87211442745029489881514515811064102429019356351722823450170249465088775249507, 39600946693670273230261533720839589755726946308581706825676138619972092199256, 4979886914346369664911891403751631037886315717549974065878536283157637402320, 22272529908653383795002294860870129574984518813560375272257703512940569602004, 100135751785995415247695765442899140606914076750888419237400306294448451415863, 85613534858376605408667291532701284666560850915689941354202786014968649139457, 38496246133430733988750968353732662162312705079114417415163071485082991344590, 55980481790171446152748793757788577465044360548729573345122559743628093363153, 71280277172994137969689292719624075379102489317199533126561191722460505314026, 110446223482446943024326135434573497276437669060614612856002207641927747194266, 16456085922385532110267651711339329146652084370610067373716816178321924748791, 101653629730678493695114228522885120593522618541788967122785214737946157867999, 74467527492811608068163160348674720595757862332879609098404557441577413104820, 41884843126443673947662657085537596879702074001592844509379139860812151553968, 29815687077578101251522932333124915023192910276895021601688368611558697857638, 44840628789800333625015337751638405696233468515566263356197320268202190223769, 102427595787595418722722430130631701884337456325150921017413824991597185452849, 2975107125099035075044003816426206055437890428466365543585422202932381886186, 94699511483779321185024950255977801474453881858185354369860946591141828290326, 31810607567540037649472765223870019465281477418301020106850480432511306591757, 75713781109794200255529510371465092460190607870508383754795316160075282283862, 55429849762380955520557448208384572772400405309708977900727750338226215580736, 71351843550447097631722656769410630908972124288367169285559142896305583201390, 84145371680533342029399999651802676680665442500082991947093355443249540103162, 18059328520840928370924328960454198116073475240703647573736616851363995779497, 83839387396741626377342400188482404639827411621171844172874897800772466334269, 25788978353065311499638204532308969267343091396798096623404684254370926606489, 46416171203559401945669998573205329748734005210989064607057470628982156110053, 42839223735347899899704913105525407073907314464785013094063759450820513757342, 88826657766811054515837039931572449230721258604658317309512814974116100196733, 53796508595019468595537500010909399217450133587528313928622717009905225347437, 56531378551320964008977461547054273860909442858252049481923559030063639435057, 48217679285988263588226655808041000825638438349841115697751615792350031644869, 64424297190010710116212288045994884168253983939992794298642423963632550451160, 46474911280506479688705284230861217499981118516937627597481370505066926962182, 64032029526907010327735757773865326038078238679652707012855320952596919166618, 5529383900219431454017233184818428510888383480088262580036064976358985800985, 69322608357555546086372761692837205200171798855109065251575534608627560525776, 76098979682650954216202311601813089916970156784884278240596741668163729505020, 91674126062289237651839995587104059408995800143522837051179562018281051100557, 90571390404208688843585603192800843878382529323359914123528861146103857760661, 72012664155317843790423022518639753138262519729890141457716216773019826138388, 66863180243825712563555363518892364864799935770917594234609418534062748300787, 5838945753982677965177087293687053018953448675487050703226841119623778529018, 4440280122867898274880560103713163505203269339591832639427292037957483435863, 113585052040012311817152621651926546174704034369418207806360593735979071392560, 96503008028224334771028807273628056037391407459560685791940303889130903300826, 67050454088005224845748627326789053425990922831763041158174139321910165797537, 56354656300386637831392267891729486882144501924180334206591055551662859511145, 108875538744684454340615686969559999736352047181969993978724550037003168200211, 105856150301241056513738964497224079598648612469774416566110150235952602587129, 103072133631485922917570773603973545510240103328265914435430955113182187850847, 105071449786380370702657927006338895312230491406739601631939501577997184496876, 101559564666645844079948496433098525970583827093303201782110972272082979410831, 45696832977481706385123240351386677526237953026854755659089774125668886575190, 92930863035601609905246064160817660898443604755800516139761871009073979122573, 7136157467487063026530735850363136522687472196852313490264738121297870888865, 62220552837071854508303645903133799707167271140998125870619424819338409845248, 71964156627499707284955744986659480338185350890617779236004729406075442337650, 56432954135882530785013240455908855171502152827770214700998108134515682426307, 24818258540494883741910232014072726664585493319546426193565346084848631309292, 68946604449180849807706382163388201284725162066731407078323925073762784383918, 78305860067531640486978712479618549593532447916095131216323237767823095149213, 40019412274222034245452650116905171509558126077504657023971877193155638952620, 6226049816877252622825028481234412013581804081798123571329306780957341285518, 72008834916679466207298598830558721788070004796890262626592503036925690499953, 24120184417962346330989331701326680837413020607663960631051474032512470756250, 106358126840983882959473879360172954895361540456426525458062716824086971706859, 96125062326106069117227627865988038851006615609777159985287487409738006940292, 33054514553432552301350757403482219452773112411443533998213496297361397155535, 41581969631676286214097564630767898944747546622643163224140263014954932195321, 22904365609725269502635057676962583581851475921482302591306344959978794545764, 64290237869656947632842147827818163107378784367086448814380499121557877108860, 30680084243764095315357070546550118749025091482163732007754607769361116153541, 13691292022145271355849518605344621718116294468846185203111794890637243685470, 25132284761110457596793743234989234799586919369754843892751414241493192284491, 12389505381820778753642609476404562621082110924974170017133920070419933455780, 71535924312884292159182314202796515340797288002505186265430063222078901533504, 12742977582401193716850400144097310370558409977576217736024733304490605337769, 75139886864475235332970108571588085544527733256425836467715638485512421268158, 106812400623906721014312287501764424395430875573845869345085033374152396156108, 91345106193584221920864389152087560188260652160092982315871571692181571481755, 65785148879985691725045496265911886841068140761050563941336015575029243383380, 1452703135528066004669796386925101704795733053841911703671961494738444465175, 44818107645190027629062089844645267760294751459286511227307352668787518517867, 26767624780451051554599928370950639364780468287039403780345758419855142782301, 73520682616655688427241752929498638616275480985470608873569998909405046919540]
B= [11, 14, 12, 1, 13, 15, 1, 14, 12, 12, 15, 6, 2, 15, 13, 15, 6, 6, 11, 12, 2, 9, 3, 15, 0, 14, 10, 10, 13, 10, 6, 13, 6, 9, 0, 4, 9, 0, 15, 5, 2, 13, 12, 12, 5, 11, 3, 3, 12, 13, 5, 5, 14, 15, 12, 10, 9, 6, 8, 5, 8, 4, 12, 1, 15, 1, 14, 11, 11, 14, 6, 10, 6, 3, 14, 10, 10, 14, 5, 15, 6, 4, 13, 1, 5, 4, 7, 4, 13, 7, 0, 14, 6, 7, 2, 14, 1, 14, 6, 9, 14, 4, 13]AA = []
BB = []
invA = inverse(A[0],q)
for i in A[1:]:AA.append(i * invA % q)
for i in range(1,103):BB.append((A[i] * invA * (B[0] * 2**252 + 2 ** 251) - (B[i] * 2 ** 252 + 2 ** 251))% q)
M = Matrix(ZZ,104,104)
for i in range(102):M[i,i] = qM[-2,i] = AA[i]M[-1,i] = BB[i]M[-2,-2] = 1
M[-1,-1] = 2 ** 251
L = M.BKZ(block_size = 22)for i in L:if abs(i[-1]) == 2 ** 251:b = B[0] * 2 ** 252 - (i[-2]) + 2 ** 251z = b * invA % qbb = []for i in range(103):# 核实if A[i] * z %q >> (256 - 4) != B[i]:breakif i == 102:print('res:',z) # res: 95734616889198769749359730283416405421230182774636752744567175201992927509949
最终:
c = b'\xda\xfc\xb7\x93\xfb\x9d\xbe\x82\xb3\xb5\x87`]}\x0b*\xd53AR\x8bb\xfeQ,\xd9\xff\xf6\n\xa2\x1b)H\\\xf24>E\xac+\x01\xf3)F\x8c\xee\xb8j\x18zb\xa8\x8b\xba\xbc\xbb\x03\xbb}\xb6\x8cO#\xeb\x0c\xce\xbd\x07\x8aWP\x90\xf2\xaep\x02\x11{\xdf\xc5'
x = 80894527713686705071002739476859399489995408997139964746730066805048451766071
y = 98898469313641499500896146398219768802603949220366063599597841309427897612653
z = 95734616889198769749359730283416405421230182774636752744567175201992927509949
key = x ^ y ^ z
key = long_to_bytes(key)
aes = AES.new(key,mode = AES.MODE_ECB)
print(aes.decrypt(c))# flag{Even_jus7_le4k_l1ttle_B1ts_We_CAN_Sovle_The_H1dd3n_Numb3r_Pr0blem}
浅记一下
这篇文其实写的很曲折,开始是想去做一下鹏程杯的题(这比赛也没打,这个月不能说不忙,只能说忙飞),然后第一题遇到剪枝+高位攻击,高位攻击中又涉及到界,所以就心血来潮的测了下coppersmith中的界。正好前几周的几个比赛都没复现,N1CTF是第一次遇到格里面的卡界题,ACTF中又遇到了,故特此在这一起记录一下
总之就是确定构造的格没问题,使劲调参还是差点,得到的结果和目标向量长度相差也不大,那可能就是卡界了,此时必须对等式进行修改,构造新的格,使得结果向量变小。
如果怎样都不行,那可能就是论文题了吧
欢迎感兴趣的师傅来进行交流讨论
相关文章:

记录一些涉及到界的题
文章目录 coppersmith的一些相关知识题1 [N1CTF 2023] e2Wrmup题2 [ACTF 2023] midRSA题3 [qsnctf 2023]浅记一下 coppersmith的一些相关知识 上界 X c e i l ( 1 2 ∗ N β 2 d − ϵ ) X ceil(\frac{1}{2} * N^{\frac{\beta^2}{d} - \epsilon}) Xceil(21∗Ndβ2−ϵ) …...

Linux秋招面试题
自己在秋招过程中遇到的Linux相关的面试题 linux查找含有“xxxx”的文件名 将/path/to/search替换为要搜索的目录路径,xxxx表示要匹配的文件名模式,其中xxxx是你要查找的字符串。这个命令将会在指定路径下递归地查找所有文件名中包含给定字符串的文件 …...

OPPO发布AndesGPT大模型;Emu Video和Emu Edit的新突破
🦉 AI新闻 🚀 OPPO发布全新ColorOS 14及自主训练的AndesGPT大模型 摘要:OPPO在2023 OPPO开发者大会上发布了全新的ColorOS 14,并正式推出了自主训练的安第斯大模型(AndesGPT)。AndesGPT拥有对话增强、个人…...

2311rust,到46版本更新
1.43.0稳定版 项(item)片段 在宏中,可用项片段把项插值到特征,实现和extern块的块体中.如: macro_rules! mac_trait {($i:item) > {trait T { $i }} } mac_trait! {fn foo() {} }这生成: trait T {fn foo() {} }围绕原语的推导类型 改进了围绕原语,引用和二进制操作的推…...

Rust根据条件删除相邻元素:dedup
文章目录 示例dedup_bydedup_by_key Rust系列:初步⚙所有权⚙结构体和枚举类⚙函数进阶⚙泛型和特征⚙并发和线程通信 示例 Rust中的动态数组Vec提供了dedup函数,用于删除相邻重复元素。此外,还提供了dedup_by和dedup_by_key,可…...
2023年(第六届)电力机器人应用与创新发展论坛-核心PPT资料下载
一、峰会简介 大会以“聚焦电力机器人创新、助力行业数字化转型、促进产业链协同发展”为主题,展示电力机器人产业全景创新技术,探讨数字化战略下电力机器人应用前景和发展趋势。为加快推进电力机器人应用拓新,助力电网数字化转型升级&#…...
Android BitmapFactory.decodeResource读取原始图片装载成原始宽高Bitmap,Kotlin
Android BitmapFactory.decodeResource读取原始图片装载成原始宽高Bitmap,Kotlin fun getOriginalBitmap(resId: Int): Bitmap {val options BitmapFactory.Options()options.inJustDecodeBounds true //只解析原始图片的宽高,不decode原始文件装载到内…...
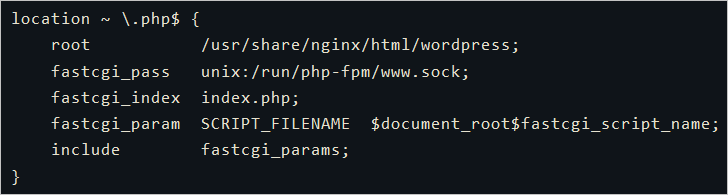
阿里云服务器 手动搭建WordPress(CentOS 8)
前提条件 已创建Linux操作系统的ECS实例,并且手动部署LNMP环境,具体操作,请参见手动部署LNMP环境(CentOS 8)。本教程使用的相关资源版本如下。 实例规格:ecs.c6.large 操作系统:公共镜像CentO…...

竞赛 题目:基于深度学习的中文对话问答机器人
文章目录 0 简介1 项目架构2 项目的主要过程2.1 数据清洗、预处理2.2 分桶2.3 训练 3 项目的整体结构4 重要的API4.1 LSTM cells部分:4.2 损失函数:4.3 搭建seq2seq框架:4.4 测试部分:4.5 评价NLP测试效果:4.6 梯度截断…...

CCF ChinaSoft 2023 论坛巡礼|软件测试产教研融合论坛
2023年CCF中国软件大会(CCF ChinaSoft 2023)由CCF主办,CCF系统软件专委会、形式化方法专委会、软件工程专委会以及复旦大学联合承办,将于2023年12月1-3日在上海国际会议中心举行。 本次大会主题是“智能化软件创新推动数字经济与社…...
浅谈WPF之控件模板和数据模板
WPF不仅支持传统的Windows Forms编程的用户界面和用户体验设计,同时还推出了以模板为核心的新一代设计理念。在WPF中,通过引入模板,将数据和算法的“内容”和“形式”进行解耦。模板主要分为两大类:数据模板【Data Template】和控…...
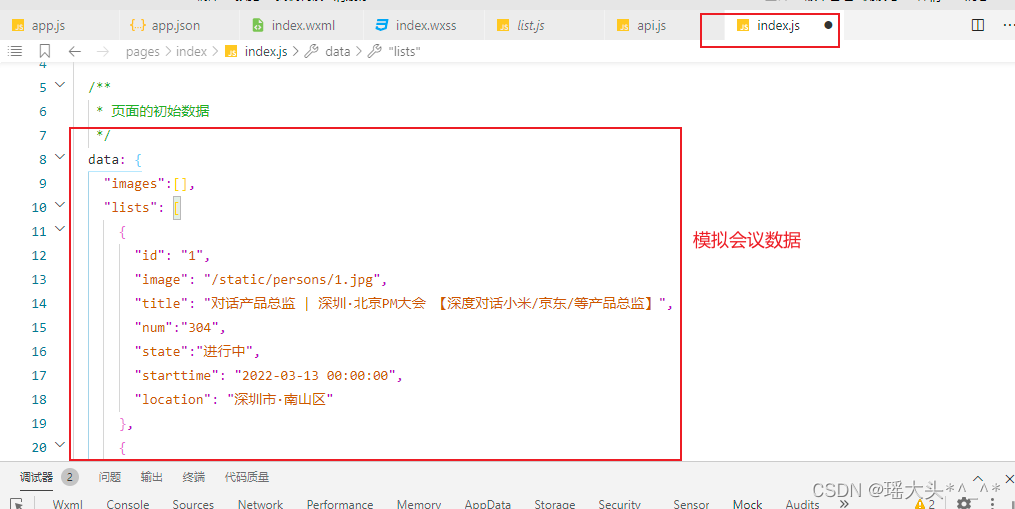
微信小程序会议OA首页-开发说明创建项目关于flex布局关于尺寸单位(rpx)关于WXS轮播图会议信息
目录 1. 创建项目 2. 关于flex布局 3. 关于尺寸单位(rpx) 4. 关于WXS 4. 轮播图 5. 会议信息 1. 创建项目 基于微信原生开发工具,稳定版 Stable Build (1.06.22010310) 创建项目前,请确定有小程序测试账号 使用向导创建一个…...
Linux上编译和安装SOFA23.06
前言 你可以直接使用编译安装好的SOFA版本Installing from all-included binaries (v23.06.00): 如果你想自己编译,可以看我下面写的内容,不过绝大多数是从官网来的,如果和官网有出入,建议还是以官网为准。 在Linux下…...

定时任务 Spring Task
一、介绍 Spring Task 是Spring框架提供的任务调度工具,可以按照约定的时间自动执行某个代码逻辑。 定位: 定时任务框架 作用: 定时自动执行某段Java代码 二、cron 表达式 cron表达式在线生成器:https://cron.qqe2.com/ 1、说明…...

golang 上传图片 --chatGPT
问:makeImgUpload(path string) 实现发送发送图片, 发送类型为 multipart/form-data gpt: 下面是一个简单的 makeImgUpload 函数的实现,用于发送图片并以 multipart/form-data 格式进行上传。请注意,此代码假设图片文件路径是正确…...
Android Studio 写一个Java调用c++ 的demo
前提条件: 本地已经配置好了ndk环境,如果没有配置好,建议参考macos 配置ndk环境-CSDN博客 这篇链接。 新建一个Empty Project 比如我这里的Project的名字是HelloJNI,包名是com.example.hellojni 然后在src目录下,右键选择Add C …...

Pandas数据操作_Python数据分析与可视化
Pandas数据操作 排序操作对索引进行排序按行排序按值排序 删除操作算数运算去重duplicated()drop_duplicates() 数据重塑层次化索引索引方式内层选取数据重塑 排序操作 对索引进行排序 Series 用 sort_index() 按索引排序,sort_values() 按值排序; Dat…...

【Debug】查询的数据量比数据库中的数据量还要多
今天前端反馈了一个bug,某个接口返回的数据很多,我到mysql数据库看了一下,查询的表名为trs_risk,其中只有1000多条数据,而页面返回有5000多条数据!! 匪夷所思啊,我定位到Mapper层的…...
nodejs微信小程序-慢性胃炎健康管理系统的设计与实现-安卓-python-PHP-计算机毕业设计
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...
二十一、数组(1)
本章概要 数组特性 用于显示数组的实用程序 一等对象返回数组 简单来看,数组需要你去创建和初始化,你可以通过下标对数组元素进行访问,数组的大小不会改变。大多数时候你只需要知道这些,但有时候你必须在数组上进行更复杂的操作…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

RLHF vs RLVR:对齐学习中的两种强化方式详解
在语言模型对齐(alignment)中,强化学习(RL)是一种重要的策略。而其中两种典型形式——RLHF(Reinforcement Learning with Human Feedback) 与 RLVR(Reinforcement Learning with Ver…...
数据挖掘是什么?数据挖掘技术有哪些?
目录 一、数据挖掘是什么 二、常见的数据挖掘技术 1. 关联规则挖掘 2. 分类算法 3. 聚类分析 4. 回归分析 三、数据挖掘的应用领域 1. 商业领域 2. 医疗领域 3. 金融领域 4. 其他领域 四、数据挖掘面临的挑战和未来趋势 1. 面临的挑战 2. 未来趋势 五、总结 数据…...
