C++构造函数 拷贝构造函数 括号法显示法隐式转换法实现类
一.无参构造 & 有参构造 & 拷贝构造函数
拷贝的是自己所属的类,也就是克隆自己。
所以传参要穿自己的类名。
克隆归克隆,但是不能把本身给改了,所以参数前要加const。
class Person
{
public:int age;public:Person(){cout<<"Person的构造函数"<<endl;}Person(int a){age = a;cout<<"Person的有参构造函数"<<endl;}//拷贝构造函数Person(const Person &p){// 将传入的人身上的所有属性,拷贝到我身上。age = p.age;}};
二.三种方法调用构造函数(类的实现)
//1.括号法调用Person p1; // 调用默认构造函数 (调默认构造函数时不能加括号,否则编译器会认为是声明)Person p2(10); //调用有参构造函数Person p3(p2); //调用拷贝构造函数//2.显示法Person p2 = Person(10); //调用有参构造Person p3 = Person(p2); //调用拷贝构造//3.隐式转换法Person p4 = 10; //相当于 Person p4 = Person(10);Person p5 = p4; //拷贝构造
相关文章:

C++构造函数 拷贝构造函数 括号法显示法隐式转换法实现类
一.无参构造 & 有参构造 & 拷贝构造函数 拷贝的是自己所属的类,也就是克隆自己。 所以传参要穿自己的类名。 克隆归克隆,但是不能把本身给改了,所以参数前要加const。class Person { public:int age;public:Person(){cout<<&q…...

FreeRTOS中的内存分配策略
FreeRTOS为内存管理提供了几种不同的策略,分别由heap_1.c至heap_5.c实现。以下是每种策略: heap_1.c: 最简单的策略。只允许一次性的内存分配。不允许内存释放。对于只分配内存但不释放的系统特别有用,如仅在启动时分配任务和队列的系统。内存…...
HP惠普光影精灵7笔记本Victus by HP 16.1英寸游戏本16-d0000原装出厂Windows11.21H2预装OEM系统
下载链接:https://pan.baidu.com/s/1LGNeQR1AF1XBJb5kfZca5w?pwdhwk6 提取码:hwk6 可适用的型号: 16-d0111tx,16-d0112tx,16-d0125tx,16-d0127tx,16-d0128tx,16-d0129tx&#…...
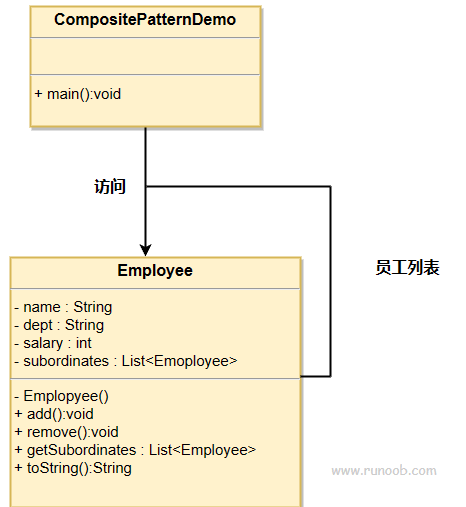
组合模式 rust和java的实现
文章目录 组合模式介绍实现javarsut 组合模式 组合模式(Composite Pattern),又叫部分整体模式,是用于把一组相似的对象当作一个单一的对象。组合模式依据树形结构来组合对象,用来表示部分以及整体层次。这种类型的设计…...

大数据基础设施搭建 - MySQL
文章目录 一、检查是否安装过MySQL二、上传安装包三、安装MySQL3.1 安装mysql依赖3.2 安装mysql-client3.3 安装mysql-server 四、启动MySQL五、配置MySQL5.1 修改密码(1)查看密码(2)登陆(3)设置复杂密码&a…...

二叉树递归遍历
能帮到你的话,就给个赞吧 😘 二叉树遍历算法 指遍历一遍二叉树就能得到答案 什么是二叉树遍历 二叉树遍历 前中后序遍历 递归遍历 3种时间节点 递归遍历会依次遍历到每个节点。 而前中后序则是在递归遍历的基础上选择操作发生的时间。 递归遍历 …...
【ArcGIS Pro二次开发】:CC工具箱1.1.1更新_免费_安装即可用
CC工具箱1.1.1更新【2023.11.15】 使用环境要求:ArcGIS Pro 3.0 一、下载链接 工具安装文件及使用文档: https://pan.baidu.com/s/1OJmO6IPtMfX_vob3bMtvEg?pwduh5rhttps://pan.baidu.com/s/1OJmO6IPtMfX_vob3bMtvEg?pwduh5r 二、使用方法 1、在下…...
Dubbo的优雅下线原理分析
文/朱季谦 Dubbo如何实现优雅下线? 这个问题困扰了我一阵,既然有优雅下线这种说法,那么,是否有非优雅下线的说法呢? 这,还真有。 可以从linux进程关闭说起,其实,我们经常使用到杀…...

leetcode做题笔记2342. 数位和相等数对的最大和
给你一个下标从 0 开始的数组 nums ,数组中的元素都是 正 整数。请你选出两个下标 i 和 j(i ! j),且 nums[i] 的数位和 与 nums[j] 的数位和相等。 请你找出所有满足条件的下标 i 和 j ,找出并返回 nums[i] nums[j]…...

c# YOLOV5目标检测部署
using Emgu.CV; using Emgu.CV.CvEnum; using Emgu.CV.Dnn; using Emgu.CV.Structure; using Emgu.CV.Util...

学习笔记6——垃圾回收
学习笔记系列开头惯例发布一些寻亲消息 链接:https://baobeihuijia.com/bbhj/contents/3/190801.html java垃圾回收(stop the world) 专注于堆和方法区的垃圾回收,年轻代,老年代,永久代判断对象是否还存…...
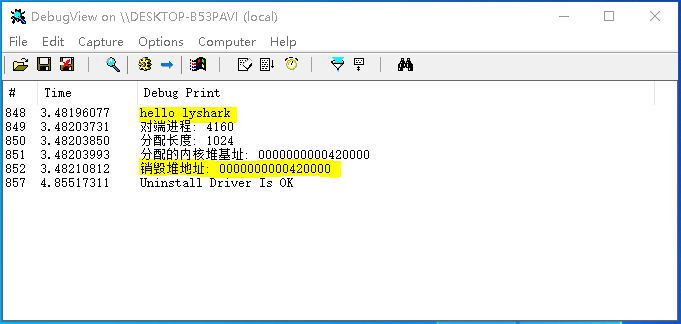
3.1 Windows驱动开发:内核远程堆分配与销毁
在开始学习内核内存读写篇之前,我们先来实现一个简单的内存分配销毁堆的功能,在内核空间内用户依然可以动态的申请与销毁一段可控的堆空间,一般而言内核中提供了ZwAllocateVirtualMemory这个函数用于专门分配虚拟空间,而与之相对应…...
C++: 模板初阶
文章目录 一. 泛型编程二. 函数模板函数模板的原理函数模板的实例化隐式实例化: 让编译器根据实参推演模板参数的实际类型显示实例化: 在函数名后的<>中制定模板参数的世纪类型 模板参数的匹配原则 三. 类模板类模板的定义格式类模板的实例化 一. 泛型编程 如何实现一个…...
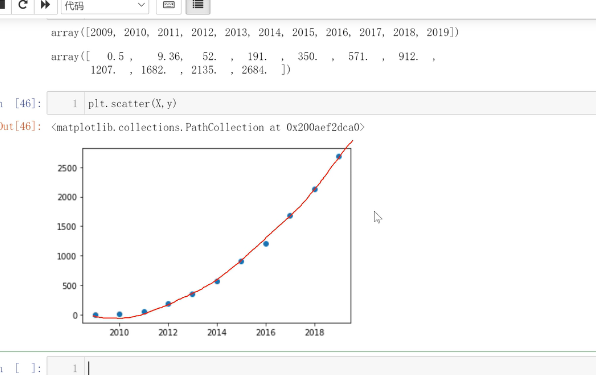
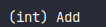
人工智能基础_机器学习036_多项式回归升维实战3_使用线性回归模型_对天猫双十一销量数据进行预测_拟合---人工智能工作笔记0076
首先我们拿到双十一从2009年到2018年的数据 可以看到上面是代码,我们自己去写一下 首先导包,和准备数据 from sklearn.linear_model import SGDRegressor import numpy as np import matplotlib.pyplot as plt X=np.arange(2009.2020)#左闭右开,2009到2019 获取从2009到202…...

【算法挨揍日记】day29——139. 单词拆分、467. 环绕字符串中唯一的子字符串
139. 单词拆分 139. 单词拆分 题目描述: 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。 注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。 解题思路&am…...

YOLOv8-Seg改进:轻量级Backbone改进 | VanillaNet极简神经网络模型 | 华为诺亚2023
🚀🚀🚀本文改进:一种极简的神经网络模型 VanillaNet,支持vanillanet_5, vanillanet_6, vanillanet_7, vanillanet_8, vanillanet_9, vanillanet_10, vanillanet_11等版本,相比较yolov8-seg各个版本如下: layersparametersgradientsGFLOPsvanillanet_521230017523...

解决Requests中使用httpbin服务器问题:自定义URL的实现与验证
问题背景 在使用Python的Requests模块进行单元测试时,可能会遇到无法使用本地运行的httpbin服务器进行测试的问题。这是因为测试脚本允许通过环境变量HTTPBIN_URL指定用于测试的本地httpbin实例,但在某些测试用例中,URL是硬编码为httpbin.or…...
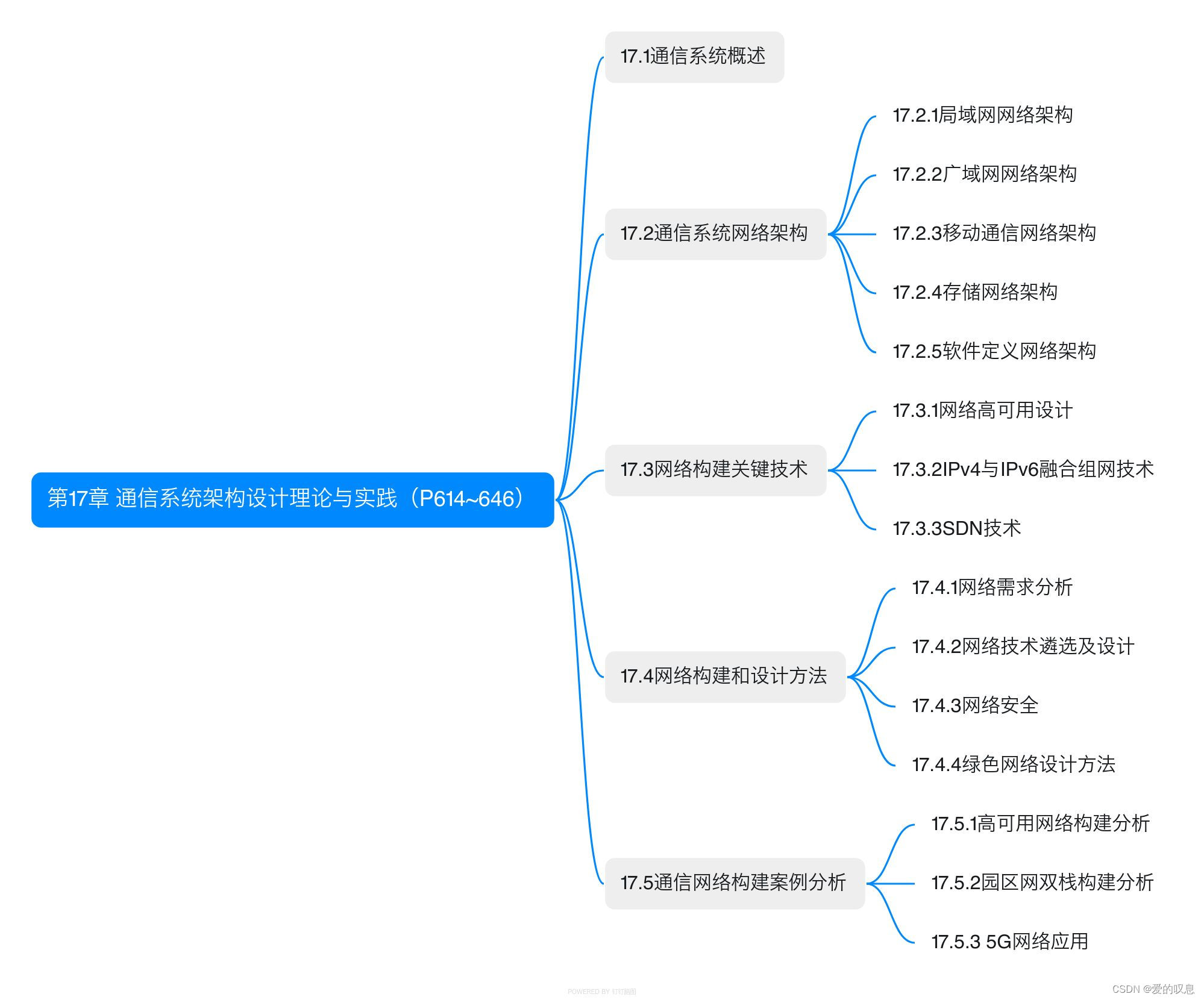
软考-高级-系统架构设计师教程(清华第2版)【第17章 通信系统架构设计理论与实践(P614~646)-思维导图】
软考-高级-系统架构设计师教程(清华第2版)【第17章 通信系统架构设计理论与实践(P614~646)-思维导图】 课本里章节里所有蓝色字体的思维导图...
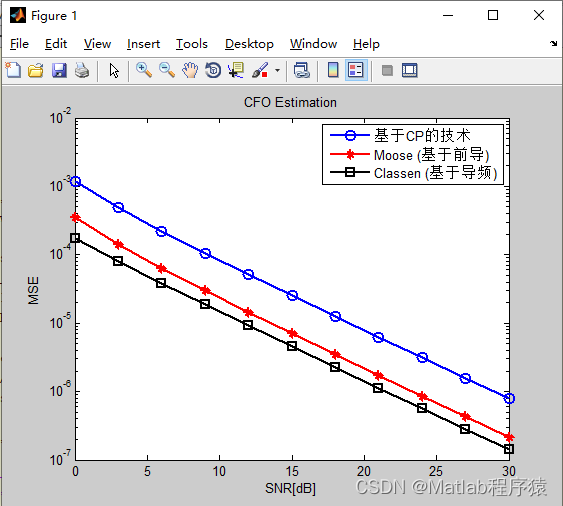
【MATLAB源码-第82期】基于matlab的OFDM系统载波频移偏差(CFO)估计,对比三种不同的方法。
操作环境: MATLAB 2013b 1、算法描述 正交频分复用(OFDM)系统中的载波频率偏移(CFO)估计是一项关键技术,用于确保数据传输的准确性和效率。CFO通常由于振荡器频率不匹配和多普勒频移引起。不同的CFO估计…...
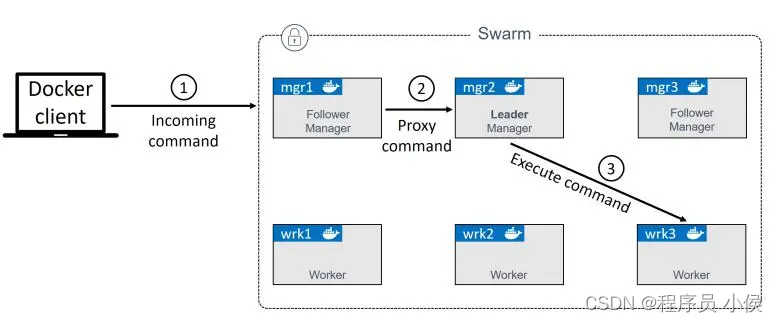
Docker Swarm: 容器编排的力量和优势深度解析
文章目录 Docker Swarm的核心概念1. 节点(Node)2. 服务(Service)3. 栈(Stack) 使用Docker Swarm1. 初始化Swarm2. 加入节点3. 创建服务4. 扩展和缩减服务5. 管理栈6. 管理服务更新 Docker Swarm的优势深度解…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
