当前位置： 首页 > news >正文

数据存储模型

news 2026/2/10 14:50:26

1、前言

        写点什么东西呢

之前大学毕设搞了个高并发模型，里面使用到了select模型，里面用到了一个内存池，支持多客户端连接、登录、消息发送，现在工作经验三年多了，开发经验积累了不少，但是对喜爱的C++的一些知识有一些遗忘，想把之前的东西都捡起来。刚好最近新买了一台14700KF的主机，纯用来打游戏些许有点小浪费，琢磨捣鼓捣鼓，把在新公司学到了一些小东西加进去，也可以应用到我的高并发服务模型里面，好不好用再说，先得动手，开搞开搞。

        之前的毕设：来自QfEifeIyU的HighConcurrencyServer

预想着是搞一个存储数据的服务，类似于Redis，部署起来可以当然没有那么牛逼，你可以理解，能读到数据就行。思路大概是这样，看看我会搞到什么进度吧

        1、服务运行起来，预加载数据到内存

        2、使用 IOCP，监听客户端连接

        3、客户端连接服务器，然后读取内存数据

2、准备动作

        今天是开发环境的部署。打算部署一个VScode。这里不打算写教程，不过我会把部署好的参考链接放进来。

        看了一下配置比较麻烦，换成Visual Studio吧，嘿嘿

相关文章：

数据存储模型

1、前言 写点什么东西呢 之前大学毕设搞了个高并发模型，里面使用到了select模型，里面用到了一个内存池，支持多客户端连接、登录、消息发送，现在工作经验三年多了，开发经验积累了不少，但是对喜爱的C的一些知…...

编程日记 2023/11/19 18:33:40

vue3+vant 实现树状多选组件

vue3vant 实现树状多选组件 需求描述效果图代码父组件引用selectTree组件 tree组件数据格式 需求描述 移动端需要复刻Pc端如上图的功能组件，但vant无组件可用，所以自己封装一个。 效果图 代码 父组件引用 import TreeSelect from "/selectTree.vu…...

编程日记 2023/11/19 18:32:39

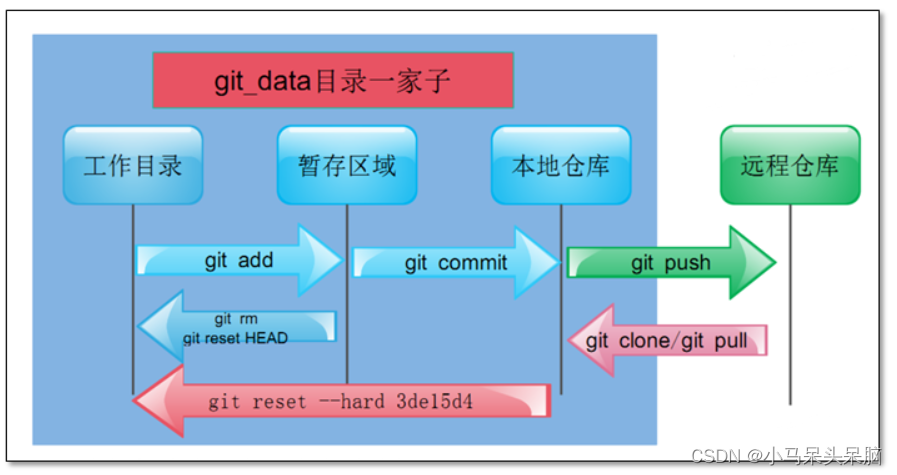
Git安装与常用命令

Git简介： Git是一个开源的分布式版本控制系统，用于敏捷高效地处理任何或大或小的项目。Git是Linus Torvalds为了帮助管理Linux内核开发而开发的一个开放源代码的版本控制软件。Git与常用的版本控制工具CVS、Subversion等不同，它采用了分布式…...

编程日记 2023/11/19 18:31:37

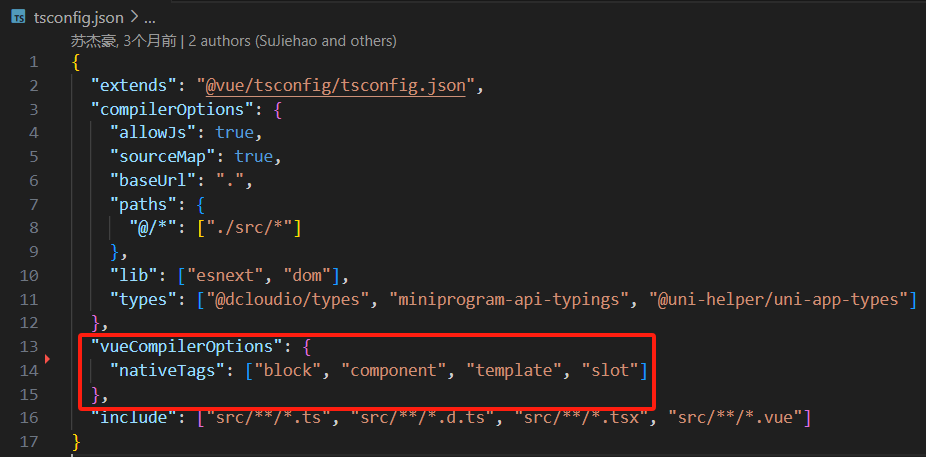
uni-app 使用vscode开发uni-app

安装插件 uni-create-view 用于快速创建页面 配置插件 创建页面 输入页面名称&#xff0c;空格&#xff0c;顶部导航的标题&#xff0c;回车 自动生成页面并在pages.json中注册了路由 pages\login\login.vue <template><div class"login">login</d…...

编程日记 2023/11/19 18:30:36

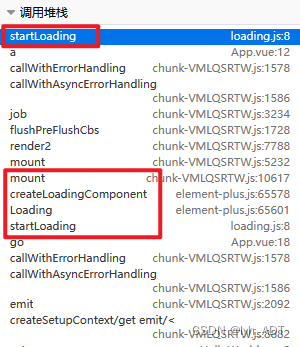
单线程的JS中Vue导致的“线程安全”问题

目录 现象分析原因 浏览器中Js是单线程的&#xff0c;当然不可能出现线程安全问题。只是遇到的问题的现象与多线程的情况十分相似&#xff0c;导致对不了解Vue实现的我怀疑起了人生… 现象 项目中用到了element-plus中的加载组件&#xff0c;简单封装了一下&#xff0c;用来保…...

编程日记 2023/11/19 18:29:35

vue2 - SuperMap3D加载基于Nginx服务生成的3DTileset模型切片服务地址

文章目录 🍍开发环境🍉1：nginx发布3Dtileset模型切片服务🍍1.1：准备3DTileset文件🍍1.2：安装nginx服务，配置相关文件1.2.1：下载nginx1.2.2：下载完解压文件如下1.2.3：将3Dtileset模型文件放置 nginx-1.24.0/html/gc 新建文件中如下：1.2.4：配置nginx服务🍉2：…...

编程日记 2023/11/19 18:27:34

新版本Spring Security 2.7 + 用法，直接旧正版粘贴

一、以前的用法&#xff1a; Configuration public class SecurityConfig extends WebSecurityConfigurerAdapter {Beanpublic PasswordEncoder passwordEncoder(){return new BCryptPasswordEncoder();}Overrideprotected void configure(HttpSecurity http) throws Exceptio…...

编程日记 2023/11/19 18:26:33

JVM——类加载器(JDK8及之前，双亲委派机制)

目录 1.类加载器的分类1.实现方式分类1.虚拟机底层实现2.JDK中默认提供或者自定义 2.类加载器的分类-启动类加载器3.类加载器的分类-Java中的默认类加载器4.类加载器的分类-扩展类加载器5.类加载器的分类-类加载器的继承 2.类加载器的双亲委派机制 类加载器&#xff08;ClassLo…...

编程日记 2023/11/19 18:24:28

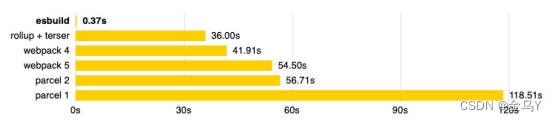
（七）什么是Vite——vite优劣势、命令

vite分享ppt&#xff0c;感兴趣的可以下载&#xff1a; ​​​​​​​Vite分享、原理介绍ppt 什么是vite系列目录&#xff1a; &#xff08;一&#xff09;什么是Vite——vite介绍与使用-CSDN博客 &#xff08;二&#xff09;什么是Vite——Vite 和 Webpack 区别&#xff0…...

编程日记 2023/11/19 18:23:27

vue之Error: Unknown option: .devServer.

背景 在使用内网穿透工具时&#xff0c;加入对应的配置&#xff0c;启动出现报错。 一、遇到的问题 报错&#xff1a; Error: Unknown option: .devServer. Check out https://babeljs.io/docs/en/babel-core/#options for more information about options. Error: Unknown …...

编程日记 2023/11/19 18:22:26

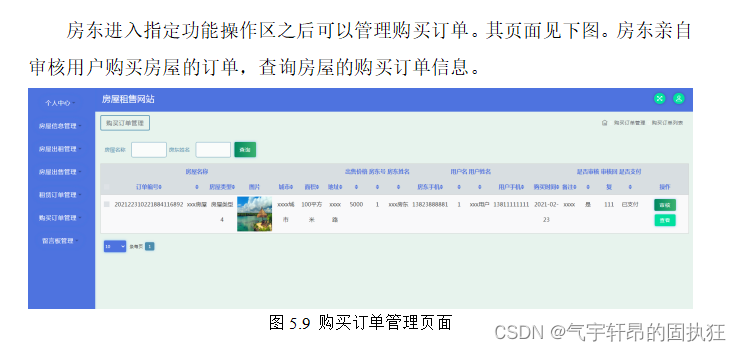
基于ssm的房屋租售网站(有报告)。Javaee项目，ssm项目。

演示视频&#xff1a; 基于ssm的房屋租售网站(有报告)。Javaee项目&#xff0c;ssm项目。 前些天发现了一个巨牛的人工智能学习网站&#xff0c;通俗易懂&#xff0c;风趣幽默&#xff0c;忍不住分享一下给大家。点击跳转到网站。 项目介绍&#xff1a; 采用M&#xff08;mode…...

编程日记 2023/11/19 18:21:26

LeeCode AutoX-4 计算几何

题意 传送门 LeeCode AutoX-4 蚂蚁爬行 题解 枚举每一对几何图形&#xff0c;判断相交性&#xff0c;用并查集维护连通性即可。总时间复杂度 O ( n 2 m ) O(n^2 m) O(n2m)&#xff0c;其中 n n n 为几何图形数量&#xff0c; m m m 为查询数量。 根据几何图形性质分类讨…...

编程日记 2023/11/19 18:20:24

Vue3 动态设置 ref

介绍 在一些场景&#xff0c;ref设置是未知的需要根据动态数据来决定&#xff0c;如表格中的input框需要我们主动聚焦&#xff0c;就需要给每一个input设置一个ref&#xff0c;进而进行聚焦操作。 Demo 点击下面截图中的编辑按钮&#xff0c;自动聚焦到相应的输入框中。 &…...

编程日记 2023/11/19 18:19:24

fast lio 2 保存每一帧的点云PCD和里程计矩阵 Odom 在txt文件

修改了源代码的 laserMapping.cpp 文件，替换为下面的代码就可以保存了，注意里面有一个路径，需要修改为你的电脑的路径 // This is an advanced implementation of the algorithm described in the // following paper: // J. Zhang and S. Singh. LOAM: Lidar Odometry an…...

编程日记 2023/11/19 18:18:23

当前主流DDos方式有哪几类

随着互联网的普及和技术的进步&#xff0c;网络安全问题日益凸显。DDoS攻击作为其中一种常见且具破坏性的攻击方式&#xff0c;受到了广泛关注。小德将带领大家一起来了解当前流行的三种DDoS攻击方式。 1. 容量耗尽攻击 容量耗尽攻击是最常见也是最直接的DDoS攻击方式。攻击者通…...

编程日记 2023/11/19 18:16:21

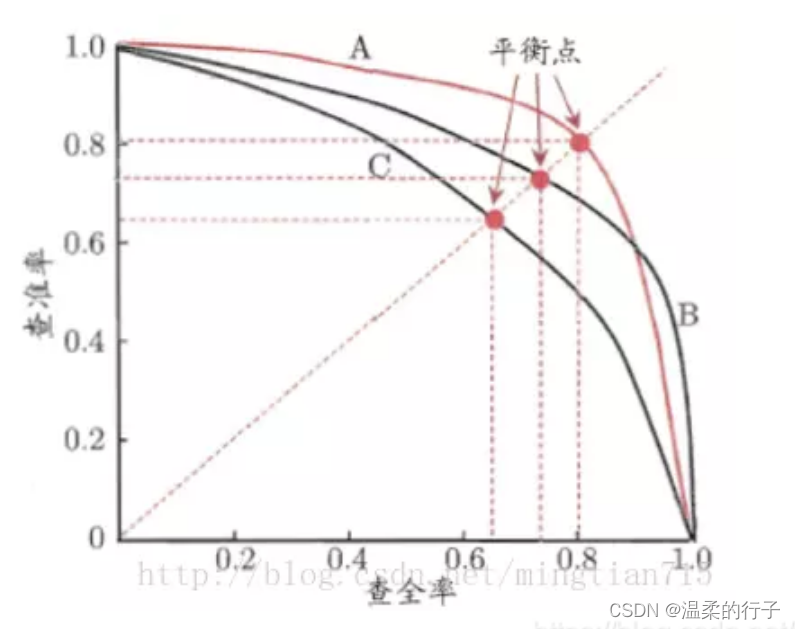
神经网络常见评价指标AUROC（AUC-ROC）、AUPR（AUC-PR）

神经网络的性能可以通过多个评价指标进行衡量&#xff0c;具体选择哪些指标取决于任务的性质。以下是神经网络中常见的评价指标&#xff1a; 准确性&#xff08;Accuracy&#xff09;&#xff1a; 准确性是最常见的分类任务评价指标&#xff0c;表示模型正确预测的样本数占总样…...

编程日记 2023/11/19 18:15:20

Apache Doris安装部署

Apache Doris安装部署 版本&#xff1a; CentOS 7.6 Apache Doris 0.14.0 编译 选择合适的版本进行下载&#xff0c;此次选择0.14.0版本 下载 | Apache Doris 一、CentOS编译 1 安装依赖 sudo yum groupinstall Development Tools && sudo yum install maven c…...

编程日记 2023/11/19 18:14:19

Excel查询时用vlookup或者xlookup时，虽然用的参数选择的是精确匹配，但是发现不能区分大小写，应该如何解决？

Excel查询时用vlookup或者xlookup时&#xff0c;虽然用的参数选择的是精确匹配&#xff0c;但是发现不能区分大小写&#xff0c;应该如何解决&#xff1f; Index函数解决 INDEX([excel1.xlsx]Sheet1!$E:$E,MATCH(1,EXACT(G5,[excel1.xlsx]Sheet1!$E:$E)*1,0))重点说明&#x…...

编程日记 2023/11/19 18:13:19

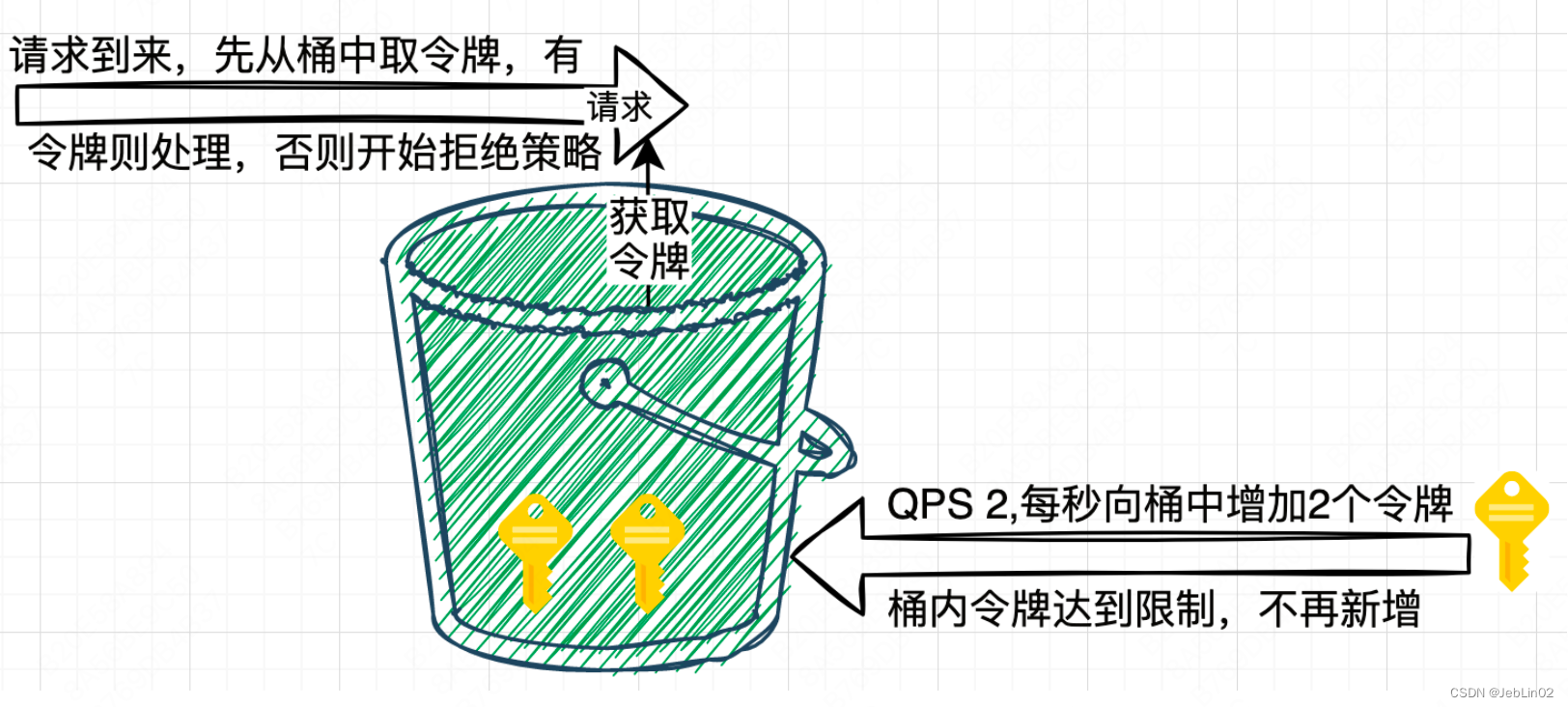
4种经典的限流算法

0、基础知识 1000毫秒内&#xff0c;允许2个请求&#xff0c;其他请求全部拒绝。 不拒绝就可能往db打请求&#xff0c;把db干爆~ interval 1000 rate 2&#xff1b; 一、固定窗口限流 固定窗口限流算法&#xff08;Fixed Window Rate Limiting Algorithm&#xff09;是…...

编程日记 2023/11/19 18:12:18

＜MySQL＞ 什么是数据库事务？事务该如何使用？

目录 一、事务的概念 二、事务的核心特性 三、事务操作中的常见BUG 3.1 脏读 3.2 不可重复读 3.3 幻读 四、隔离级别 五、使用事务 一、事务的概念 “事务”是指一组操作&#xff0c;在逻辑上是不可分割的&#xff0c;组成这组操作的各个语句&#xff0c;或者全部执行成…...

编程日记 2023/11/19 18:11:17

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造&#xff0c;完美适配AGV和无人叉车。同时&#xff0c;集成以太网与语音合成技术&#xff0c;为各类高级系统&#xff08;如MES、调度系统、库位管理、立库等&#xff09;提供高效便捷的语音交互体验。 L…...

编程新知 2026/2/8 4:23:14

springboot 百货中心供应链管理系统小程序

一、前言 随着我国经济迅速发展&#xff0c;人们对手机的需求越来越大&#xff0c;各种手机软件也都在被广泛应用&#xff0c;但是对于手机进行数据信息管理&#xff0c;对于手机的各种软件也是备受用户的喜爱&#xff0c;百货中心供应链管理系统被用户普遍使用&#xff0c;为方…...

编程新知 2026/2/8 20:41:49

Lombok 的 @Data 注解失效，未生成 getter/setter 方法引发的HTTP 406 错误

HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误&#xff0c;它们的含义、原因和解决方法都有显著区别。以下是详细对比&#xff1a; 1. HTTP 406 (Not Acceptable) 含义&#xff1a; 客户端请求的内容类型与服务器支持的内容类型不匹…...

编程新知 2026/2/1 20:49:03

HTML 列表、表格、表单

1 列表标签 作用&#xff1a;布局内容排列整齐的区域 列表分类&#xff1a;无序列表、有序列表、定义列表。 例如&#xff1a; 1.1 无序列表 标签&#xff1a;ul 嵌套 li&#xff0c;ul是无序列表&#xff0c;li是列表条目。 注意事项&#xff1a; ul 标签里面只能包裹 li…...

编程新知 2026/1/24 22:33:33

现有的 Redis 分布式锁库（如 Redisson）提供了哪些便利？

现有的 Redis 分布式锁库&#xff08;如 Redisson&#xff09;相比于开发者自己基于 Redis 命令&#xff08;如 SETNX, EXPIRE, DEL&#xff09;手动实现分布式锁&#xff0c;提供了巨大的便利性和健壮性。主要体现在以下几个方面&#xff1a; 原子性保证 (Atomicity)&#xff…...

编程新知 2025/9/23 11:26:04

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器

拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件&#xff1a; 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

编程新知 2026/2/10 0:52:03

【Veristand】Veristand环境安装教程-Linux RT / Windows

首先声明&#xff0c;此教程是针对Simulink编译模型并导入Veristand中编写的&#xff0c;同时需要注意的是老用户编译可能用的是Veristand Model Framework&#xff0c;那个是历史版本&#xff0c;且NI不会再维护&#xff0c;新版本编译支持为VeriStand Model Generation Suppo…...

编程新知 2026/2/5 20:04:55

ubuntu22.04有线网络无法连接，图标也没了

今天突然无法有线网络无法连接任何设备&#xff0c;并且图标都没了 错误案例 往上一顿搜索&#xff0c;试了很多博客都不行&#xff0c;比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动&#xff0c;重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

编程新知 2026/2/6 13:01:28

2.3 物理层设备

在这个视频中&#xff0c;我们要学习工作在物理层的两种网络设备&#xff0c;分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间&#xff0c;需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质&#xff0c;假设A节点要给…...

编程新知 2026/2/10 3:55:32

C++ 类基础：封装、继承、多态与多线程模板实现

前言 C 是一门强大的面向对象编程语言&#xff0c;而类&#xff08;Class&#xff09;作为其核心特性之一&#xff0c;是理解和使用 C 的关键。本文将深入探讨 C 类的基本特性&#xff0c;包括封装、继承和多态&#xff0c;同时讨论类中的权限控制&#xff0c;并展示如何使用类…...

编程新知 2025/11/15 8:22:14