SPASS-回归分析
回归分析概述
确定性关系与非确定性关系
变量与变量之间的关系分为确定性关系和非确定性关系，函数表达确定性关系。研究变量间的非确定性关系，构造变量间经验公式的数理统计方法称为回归分析。
回归分析基本概念
回归分析是指通过提供变量之间的数学表达式来定量描述变量间相关关系的数学过程，这一数学表达式通常称为经验公式。我们不仅可以利用概率统计知识，对这个经验公式的有效性进行判定，同时还可以利用这个经验公式，根据自变量的取值预测因变量的取值。如果是多个因素作为自变量的时候，还可以通过因素分析，找出哪些自变量对因变量的影响是显著的，哪些是不显著的。
回归分析的一般步骤
第1步 确定回归方程中的因变量和自变量。
第2步 确定回归模型。
第3步 建立回归方程。
第4步 对回归方程进行各种检验。
拟合优度检验
回归方程的显著性检验
回归系数的显著性检验
第5步 利用回归方程进行预测。
线性回归分析
基本概念
线性回归假设因变量与自变量之间为线性关系，用一定的线性回归模型来拟合因变量和自变量的数据，并通过确定模型参数来得到回归方程。根据自变量的多少，线性回归可有不同的划分。当自变量只有一个时，称为一元线性回归，当自变量有多个时，称为多元线性回归。
统计原理
一元回归方程和多元回归方程
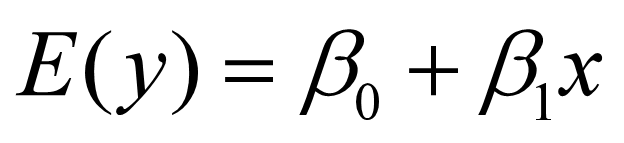
相关文章：
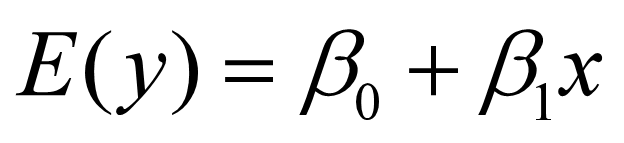
SPASS-回归分析
回归分析概述 确定性关系与非确定性关系 变量与变量之间的关系分为确定性关系和非确定性关系，函数表达确定性关系。研究变量间的非确定性关系，构造变量间经验公式的数理统计方法称为回归分析。 回归分析基本概念 回归分析是指通过提供变量之间的数学表达式来定量描述变量间…...
【使用vscode在线web搭建开发环境--code-server搭建】
官方版本下载 https://github.com/coder/code-server/releases?q4.0.0&expandedtrue使用大于版本3.8.0,因为旧版本有插件市场不能访问的情况版本太高需要更新环境依赖 拉取安装包 []# wget "https://github.com/coder/code-server/releases/download/v4.0.0/code-…...
c++ list容器使用详解
list容器概念 list是一个双向链表容器，可高效地进行插入删除元素。 List 特点： list不可以随机存取元素，所以不支持at.(position)函数与[]操作符。可以对其迭代器执行，但是不能这样操作迭代器：it3使用时包含 #includ…...
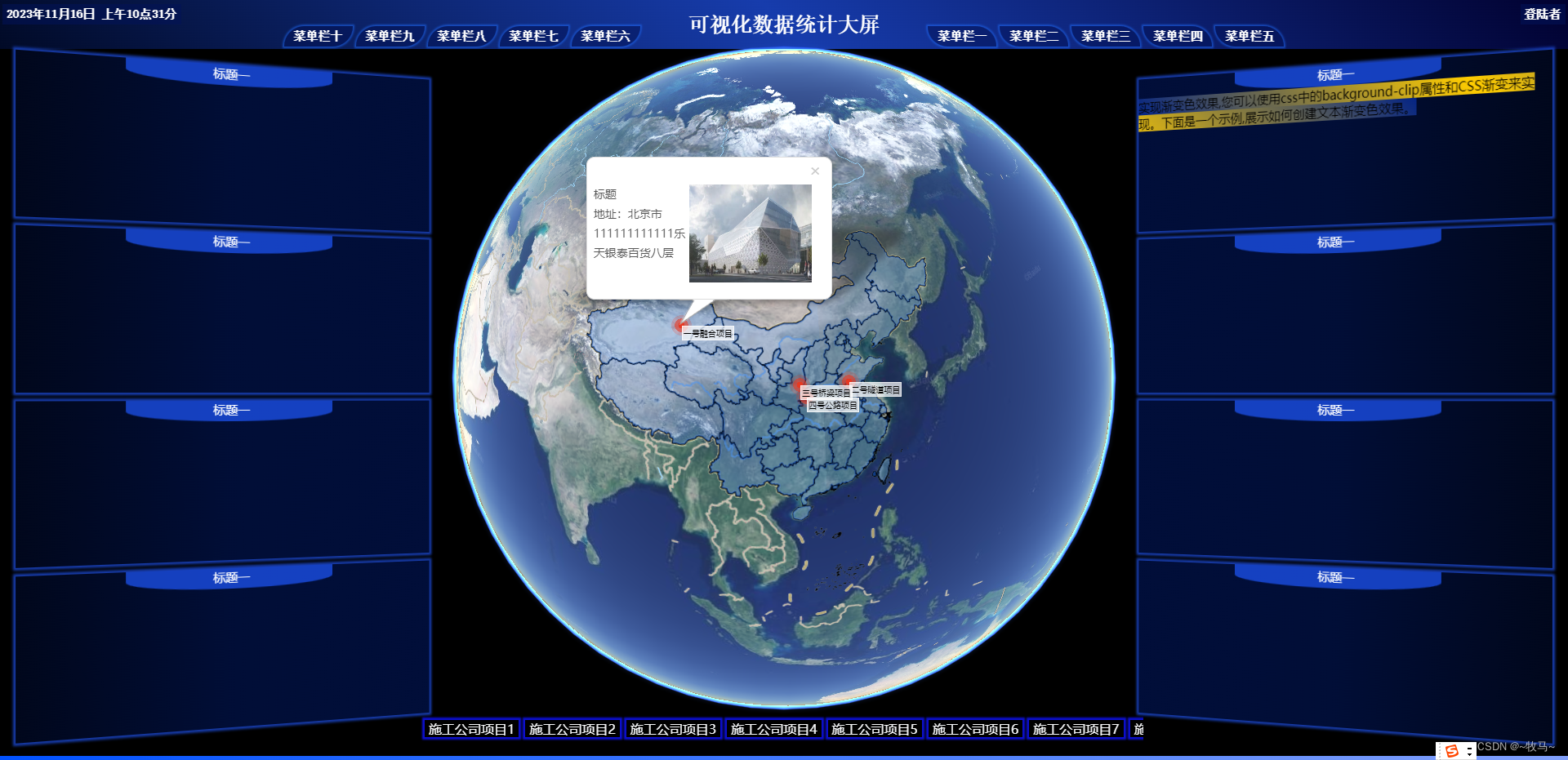
【案例】可视化大屏
人狠话不多，直接上效果图 这里放的地图自己去实现吧，如果也想实现3D地球话，等笔者那天有心情写篇文章； 说明：script中methods部分代码是没用，可以直接删掉，根据个人情况去写， 内容：笔者也就对页面布局进行了设计，内容的填充就靠个人了 <template><div :sty…...
js制作动态表单
JS制作动态表单，可以通过以下步骤实现： HTML布局：在HTML中创建一个表单元素，并设置一个ID属性。 <form id"myForm"><label for"name">姓名：</label><input type"text…...
解决Kibana初始化失败报错： Unable to connect to Elasticsearch
现象： 原因： docker run生成容器的时候，指定elastic server时指向了localhost 为什么不能是localhost, 因为这个localhost指向的是容器本身的网络，而elastic用的是物理网络，两个网络是隔离的，所以如果kiba…...
流媒体服务器
市面上优秀的流媒体服务器解决方案有很多，比如SRS，Red5，EasyDarwin，nginx-rtmp，live555，mediasoup等等。 这些服务器框架各有优缺点，没有一款完美的流媒体服务器解决方案，在流媒体选…...
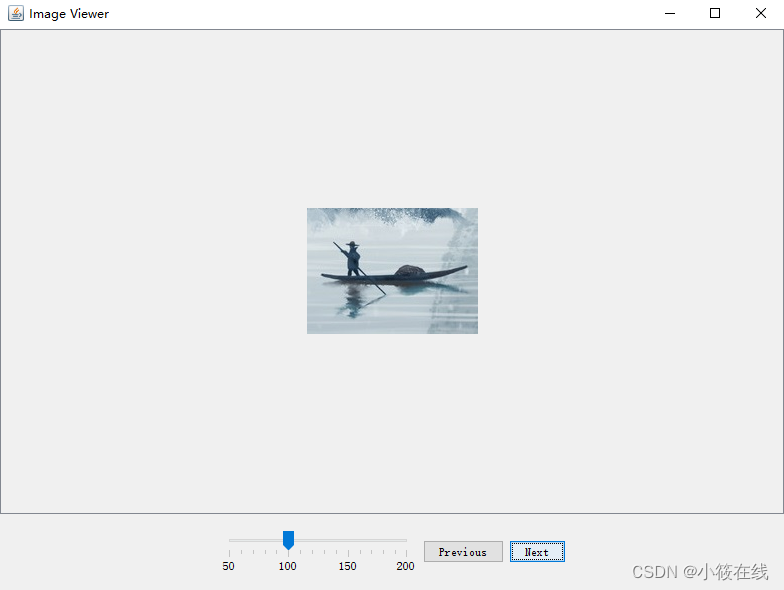
Java GUI小程序之图片浏览器
以下是一个简单的图片浏览器示例代码，它包含了图片放大缩小、拖拽、上一张/下一张查看等功能。你可以根据它进行扩展，提高用户体验。 import java.awt.BorderLayout; import java.awt.Dimension; import java.awt.event.ActionEvent; import java.awt.e…...
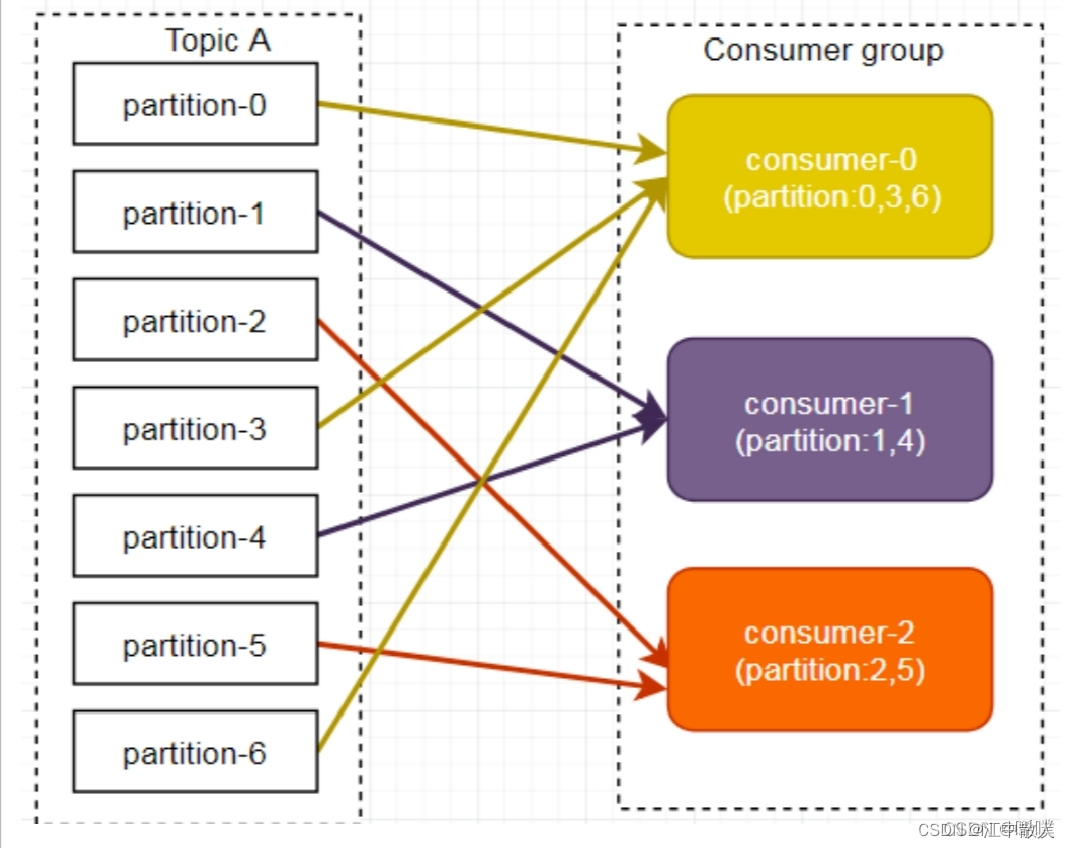
Kafka-4.1-工作原理综述
1 Kafka工作原理详解 1.1 工作流程 Kafka集群将 Record 流存储在称为 Topic 的类中，每个记录由⼀个键、⼀个值和⼀个时间戳组成。 Kafka 中消息是以 Topic 进⾏分类的，⽣产者⽣产消息，消费者消费消息，⾯向的都是同⼀个Topic。Topi…...
Linux八股文
Linux八股文 第一章 Linux简介 Linux是一种多用户、多任务，支持多线程和多CPU的操作系统，具有免费、稳定、高效的优点，一般运行在大型服务器上。 1.1 常用目录 目录说明/根目录，有且仅有一个，一般只存放目录/home家目…...
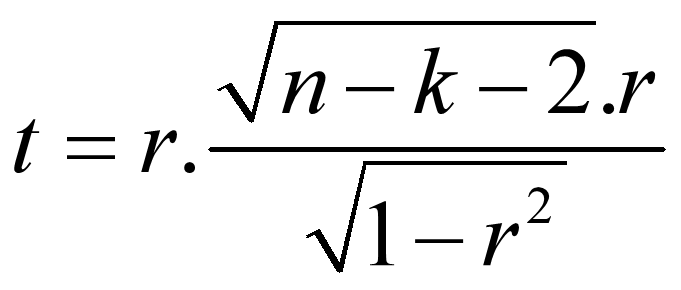
SPASS-偏相关分析
基本概念 偏相关分析的任务就是在研究两个变量之间的线性相关关系时控制可能对其产生影响的变量，这种相关系数称为偏相关系数。偏相关系数的数值和简单相关系数的数值常常是不同的，在计算简单相关系数时，所有其他自变量不予考虑。 统计原理 控制一个变量和控制两个变量的偏…...
第二证券：今日投资前瞻：小米汽车引关注 全球风光有望持续高速发展
昨日，两市股指盘中轰动上扬，深成指、创业板指一度涨超1%。到收盘，沪指涨0.55%报3072.83点，深成指涨0.72%报10077.96点，创业板指涨0.53%报2015.36点，北证50指数涨2.64%；两市算计成交9900亿元&…...
Docker中的RabbitMQ已经启动运行，但是管理界面打不开
文章目录 前言一、解决方法方法一方法二 总结 前言 肯定有好多小伙伴在学习RabbitMQ的过程中，发现镜像运行，但是我的管理界面怎么进不去，或者说我第一天可以进去，怎么第二天进不去了，为什么每次重新打开虚拟机都进不去…...
自动化网络图软件
由于 IT 系统的发展、最近向混合劳动力的转变、不断变化的客户需求以及其他原因，网络监控变得更加复杂。IT 管理员需要毫不费力地可视化整个网络基础设施，通过获得对网络的可见性，可以轻松发现模式、主动排除故障、确保关键设备可用性等。 为…...
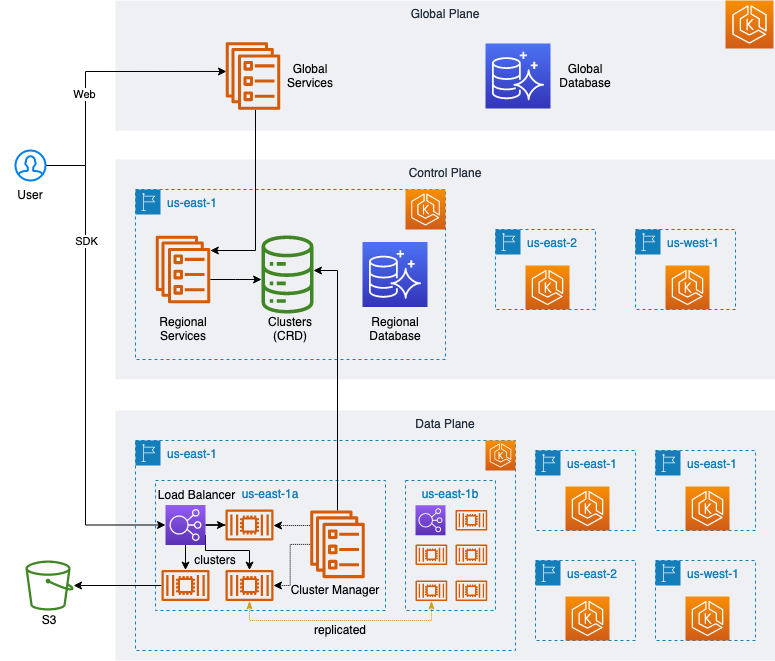
如何基于亚马逊云科技打造高性能的 SQL 向量数据库 MyScale
MyScale 是一款完全托管于亚马逊云科技，支持 SQL 的高效向量数据库。MyScale 的优势在于，它在提供与专用向量数据库相匹敌甚至优于的性能的同时，还支持完整的 SQL 语法。在这篇文章中，我们将阐述 MyScale 是如何借助亚马逊云科技的…...
《轻松入门！快速安装PyCharm，打造高效Python编程环境》
「Pycharm安装包和相关插件（Windows 64位）」https://www.aliyundrive.com/s/jByv6vjShVz 提取码: 1234 视频教程：https://www.douyin.com/video/7303106933521763596?previous_pageapp_code_link 第一步：找到一起下载的Pycharm安…...
Golang环境搭建Win10（简洁版）
Golang环境搭建Win10 Golang环境搭建(Win10)一、前言二、Golang下载三、配置环境变量3.1、配置GOROOT3.2、配置GOPATH3.3、配置GOPROXY代理 Golang环境搭建(Win10) 一、前言 Go（又称 Golang）是 Google 的 Robert Griesemer，Rob Pike 及 Ken…...
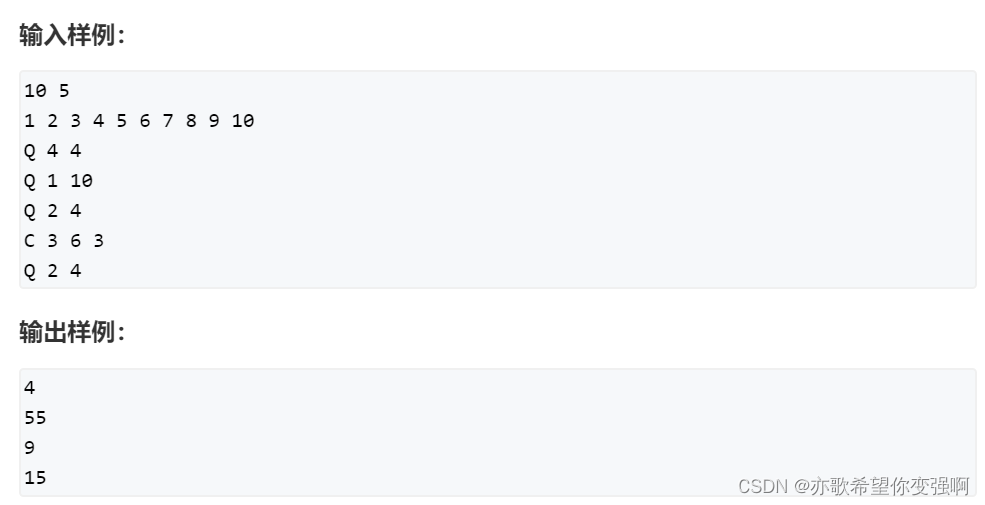
【算法每日一练]-分块（保姆级教程 篇1）POJ3648
插讲一下分块 题目：（POJ 3648） 一个简单的整数问题 前缀和往往用于静态的不会修改的区间和。遇到经常修改的区间问题，就要用分块或线段树来维护了。 分块算法是优化后的暴力，分块算法有时可以维护一些线段树维护不了的…...
【华为OD题库-026】通过软盘拷贝文件-java
题目 有一名科学家想要从一台古董电脑中拷贝文件到自己的电脑中加以研究。但此电脑除了有一个3.5寸软盘驱动器以外，没有任何手段可以将文件拷贝出来，而且只有一张软盘可以使用。因此这一张软盘是唯一可以用来拷贝文件的载体。科学家想要尽可能多地将计算…...
定量数据和定性数据
定量数据本质上是数值，应该是衡量某样东西的数量。 定性数据本质上是类别，应该是描述某样东西的性质。 全部的数据列如下，其中既有定性列也有定量列； import pandas as pdpd.options.display.max_columns None pd.set_option(e…...
大模型系列（掩码注意力，KV Cache，GQA）
文章目录一. 掩码注意力二. KV Cache三. GQA (Grouped-Query Attention，分组查询注意力)一. 掩码注意力 假设我们正在训练一个语言模型（比如GPT），当前抓取到的一条训练数据是一句话：bos 我 爱吃 苹果（bos …...
基于模糊控制的改进DWA算法功能详解
改进动态窗口DWA算法，模糊控制自适应调整评价因子权重，matlab代码 这段代码是一个基于动态窗口法（Dynamic Window Approach，DWA）的路径规划算法的实现。下面我将对代码进行分析，并解释算法的优势、需要注意…...
OpenClaw任务监控实战：Phi-3-vision-128k-instruct长流程管理
OpenClaw任务监控实战：Phi-3-vision-128k-instruct长流程管理 1. 为什么需要长流程监控 去年夏天，我接手了一个需要处理大量图文混合数据的项目。最初尝试用传统脚本串联处理，结果发现当任务运行到第37小时突然中断时，我甚至不知…...
8-Bit硬边框UI如何提升AI工具体验？Pixel Fashion Atelier交互反馈机制解析
8-Bit硬边框UI如何提升AI工具体验？Pixel Fashion Atelier交互反馈机制解析 1. 像素化界面设计的创新价值 在AI工具同质化严重的今天，Pixel Fashion Atelier通过8-Bit硬边框UI设计带来了全新的用户体验。这种设计不仅仅是视觉风格的改变，更是…...
三菱FX3U V50 stm32f407底层源码支持以太网4G模块 FX3U源码V50.0版
三菱FX3U V50 stm32f407底层源码支持以太网4G模块 FX3U源码V50.0版，基于STM32F407平台，全新程序架构，指令丰富，注释详细。6、2021年3月1日，修复无法在线监视D8000~D255的值，并修复在线监视卡死的问题。5、…...
华为网络设备高危命令大全
在网络运维现场，最怕的不是设备坏，而是“人手滑”。 很多事故不是硬件问题，也不是链路问题，而是一条命令敲下去，业务直接“蒸发”。 我带过不少一线工程师，有个共同问题： 命令会用，但不知道哪些“不能随便用”。 这篇文章，不讲基础、不讲概念，直接把华为网络设备中…...
夸克网盘自动化助手：告别手动操作，享受智能云存储管理
夸克网盘自动化助手：告别手动操作，享受智能云存储管理 【免费下载链接】quark_auto_save 夸克网盘签到、自动转存、命名整理、发推送提醒和刷新媒体库一条龙 项目地址: https://gitcode.com/gh_mirrors/qu/quark_auto_save 还在为每天重复检查夸克…...
抖音音频高效提取：用douyin-downloader提升自媒体人90%素材处理效率
抖音音频高效提取：用douyin-downloader提升自媒体人90%素材处理效率 【免费下载链接】douyin-downloader A practical Douyin downloader for both single-item and profile batch downloads, with progress display, retries, SQLite deduplication, and browser f…...
ai赋能vue开发，让快马平台智能生成数据可视化仪表盘
最近在做一个数据可视化项目，正好体验了用AI辅助Vue3开发的全流程。不得不说，现在的AI工具确实让前端开发效率提升了不少。下面分享下我是如何通过InsCode(快马)平台快速实现一个智能数据仪表盘的。 需求分析与技术选型 首先需要明确仪表盘的核心功能&am…...
零基础掌握Pulover‘s Macro Creator：自动化任务全攻略
零基础掌握Pulovers Macro Creator：自动化任务全攻略 【免费下载链接】PuloversMacroCreator Automation Utility - Recorder & Script Generator 项目地址: https://gitcode.com/gh_mirrors/pu/PuloversMacroCreator 你是否每天都在重复相同的电脑操作&…...