线性代数学习-1
线性代数学习-1
- 行图像和列图像
- 行图像
- 列图像
- 总结
本文转载于https://herosunly.blog.csdn.net/article/details/88698381
该文章本人认为十分有用，便自己敲一遍笔记加固印象
原文链接 原文
这个笔记感觉比我老师讲的更加透彻，清晰。很好的展示了线性代数的原理，强烈推荐看原文
行图像和列图像
线性方程的几何图像
线性代数的一个重要问题是求解n元一次方程组。例如下面的二元方程组
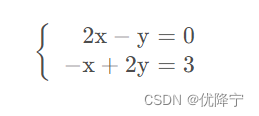
用矩阵表示如下所示：
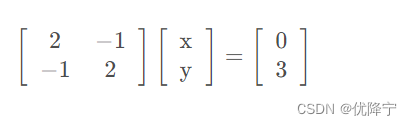
其中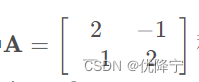
称为是系数矩阵，未知数向量
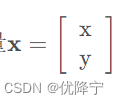，等号右侧的向量记为b。可得Ax=b
行图像
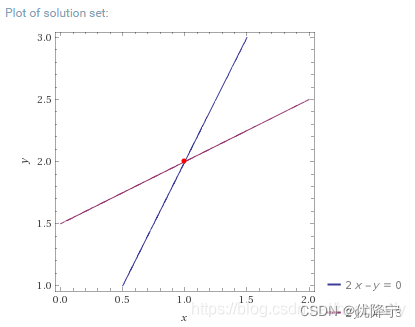
行图像和解析几何的结果是一致的，即每个方程的图像为一条直线。绘制出两个方程组对应的直线，两条直线交点即为方程组的解x=1，y=2。
列图像
在列图像中，我们将系数举证按列划分，即把矩阵分解成若干列向量的形式，则求解原方程可转化为为寻找列向量的线性组合来构成向量b。
向量的线性组合是课程的重要概念之一。其中线性组合指的是向量的加法和向量的数乘。其中向量的加法需满足平行四边形法则或者三角形法则，向量的数乘指的是向量的伸缩（其中系数大于1则进行伸展，小于1则进行收缩）。其中，基向量的线性组合能够表示整个空间。
从几何上讲，我们是寻找满足如下要求的x和y，是的两者分别数乘对应的列向量之后相加得到向量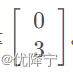
如果只是二元方程，可能还看不出来列图像的优势，如果是多元方程，就显而易见了。
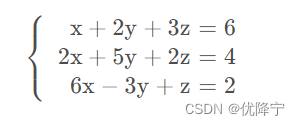
对于方程组Ax=b而言，如果改变等号右侧向量b的数值，那么对于行图像而言三个平面都改变了，而对于列图像而言，三个向量并没有发生改变，只是需要寻找一个新的组合
总结
1、行图像是将方程化成图像，而方程组组成的多个图像的交点就是方程组的解
2、列图像是将未知数的系数合并成一个列向量，用列向量来表示一个方程组
相关文章：
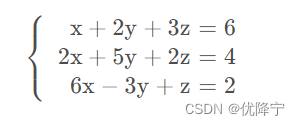
线性代数学习-1
线性代数学习-1行图像和列图像行图像列图像总结本文转载于https://herosunly.blog.csdn.net/article/details/88698381 该文章本人认为十分有用，便自己敲一遍笔记加固印象原文链接 原文这个笔记感觉比我老师讲的更加透彻，清晰。很好的展示了线性代数的原…...
人工智能写的十段代码，九个通过测试了
“抢走你工作的不会是 AI ，而是先掌握 AI 能力的人” 编程测试 1. 我想用golang实现二叉树前序，请你帮我写一下代码。 // 定义二叉树节点 type TreeNode struct {Val intLeft *TreeNodeRight *TreeNode }// 前序遍历 func PreOrderTraversal(root *Tre…...
巴塞尔问题数值逼近方法
巴塞尔问题：计算所有平方数的导数和 ∑n1∞1n2limn→∞(112122⋯1n2)\sum_{n1}^{\infty} \frac{1}{n^{2}}\lim _{n \rightarrow\infty}\left(\frac{1}{1^{2}}\frac{1}{2^{2}}\cdots\frac{1}{n^{2}}\right)n1∑∞n21n→∞lim(121221⋯n21) 其理论解为…...
【深度学习环境】Docker
1. Docker 相关安装配置 1.1 docker 安装 参考：https://www.runoob.com/docker/ubuntu-docker-install.html 1.2 nvidia-docker 安装 参考：https://zhuanlan.zhihu.com/p/37519492 1.3 代理加速 参考：https://yeasy.gitbook.io/docker_…...
基于vscode开发vue项目的详细步骤教程 2 第三方图标库FontAwesome
1、Vue下载安装步骤的详细教程(亲测有效) 1_水w的博客-CSDN博客 2、Vue下载安装步骤的详细教程(亲测有效) 2 安装与创建默认项目_水w的博客-CSDN博客 3、基于vscode开发vue项目的详细步骤教程_水w的博客-CSDN博客 目录 六、第三方图标库FontAwesome 1 安装FontAwesome 解决报…...
今天面了个腾讯拿25K出来的软件测试工程师，让我见识到了真正的天花板...
今天上班开早会就是新人见面仪式，听说来了个很厉害的大佬，年纪还不大，是上家公司离职过来的，薪资已经达到中高等水平，很多人都好奇不已，能拿到这个薪资应该人不简单，果然，自我介绍的…...
OSG三维渲染引擎编程学习之六十九：“第六章：OSG场景工作机制” 之 “6.9 OSG数据变量”
目录 第六章 OSG场景工作机制 6.9 OSG数据变量 第六章 OSG场景工作机制 作为一个成熟的三维渲染引擎，需要提供快速获取场景数据、节点等信息，具备自定义数据或动画更新接口，能接收应用程序或窗口等各类消息。OSG三维渲染引擎能较好地完成上述工作，OSG是采用什么方式或工作…...
Tektronix泰克TDP3500差分探头3.5GHz
附加功能： 带宽：3.5 GHz 差分输入电容：≤0.3 pF 差分输入电阻：100 kΩ DC pk 交流输入电压：15 V >60 dB 在 1 MHz 和 >25 dB 在 1 GHz CMRR 出色的共模抑制——减少较高共模环境中的测量误差 低电容和电阻负载…...
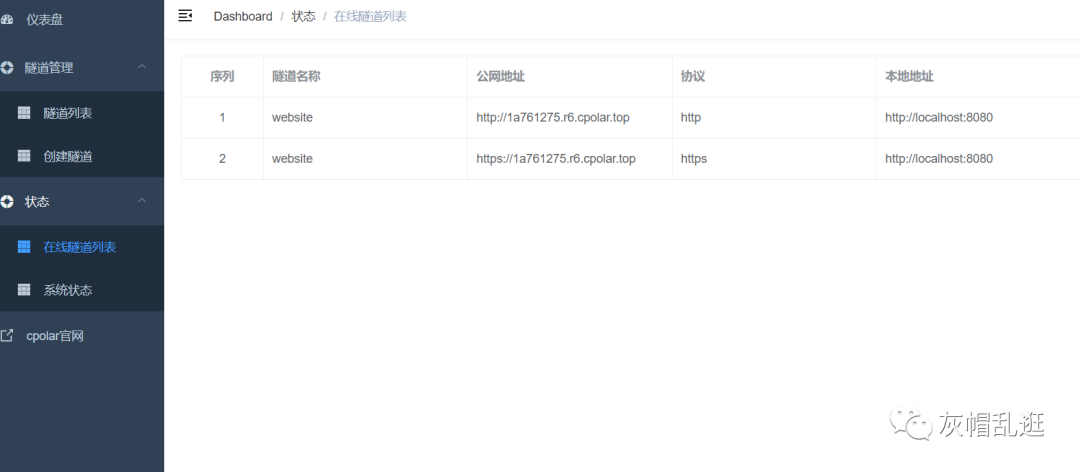
轻松实现内网穿透：实现远程访问你的私人网络
导语：内网穿透是什么？为什么我们需要它？今天我们将介绍这个令人惊叹的技术，让你实现远程访问你的私人网络。 使用内网穿透，轻松实现外网访问本地部署的网站 第一部分：什么是内网穿透？ 通俗解释…...
MySQL长字符截断
MySQL超长字符截断又名"SQL-Column-Truncation"，是安全研究者Stefan Esser在2008 年8月提出的。 在MySQL中的一个设置里有一个sql_mode选项，当sql_mode设置为default时，即没有开启STRICT_ALL_TABLES选项时（MySQLsql_mo…...
python计算量比指标
百度百科是这么写的：量比定义：股市开市后平均每分钟的成交量与过去5个交易日平均每分钟成交量之比。计算公式：量比（现成交总手数 / 现累计开市时间(分) ）/ 过去5日平均每分钟成交量。这里公式没有问题，但是…...
下拉框推荐-Suggest-SUG
什么是下拉框推荐 在我们使用各种app（飞猪）想要搜索我们想要的东西，假设我想要上海迪士尼的门票，那么精确的query是“上海迪士尼门票”，要打7个字，如果在你输入“上海”的时候app就推荐了query“上海迪士尼…...
Nmap的几种扫描方式以及相应的命令
Nmap是一款常用的网络扫描工具，它可以扫描目标网络上的主机和服务，帮助安全研究员了解目标网络的拓扑结构和安全情况。以下是Nmap的几种扫描方式以及相应的命令： 1.Ping扫描 Ping扫描可以用来探测网络上响应的主机，可以使用“-sn…...
Qt::QOpenGLWidget 渲染天空壳
在qt窗口中嵌入opengl渲染天空壳和各种立方体一 学前知识天空壳的渲染学前小知识1 立方体贴图 天空壳的渲染就是利用立方体贴图来实现渲染流程2 基础光照 光照模型3 opengl帧缓冲 如何自定义帧缓冲实现后期特效4 glsl常见的shader内置函数 glsl编程常用的内置函数二 shader代码…...
谷歌搜索技巧大全 | 谷歌高级搜索语法指令
谷歌搜索技巧是利用各种高级搜索语法或者搜索指令，让我们能够使用Google进行精确化的搜索，外贸找客户和学术文件查找都可以应用到这些搜索技巧。(大部分命令也适用百度搜索)。Google通过互联网收集数据，抓取有意义的信息，将其存储…...
JAVA开发（JAVA垃圾回收的几种常见算法）
JAVA GC 是JAVA虚拟机中的一个系统或者说是一个服务，专门是用于内存回收，交还给虚拟机的功能。 JAVA语言相对其他语言除了跨平台性，还有一个最重要的功能是JAVA语言封装了对内存的自动回收。俗称垃圾回收器。所以有时候我们不得不承认&#…...
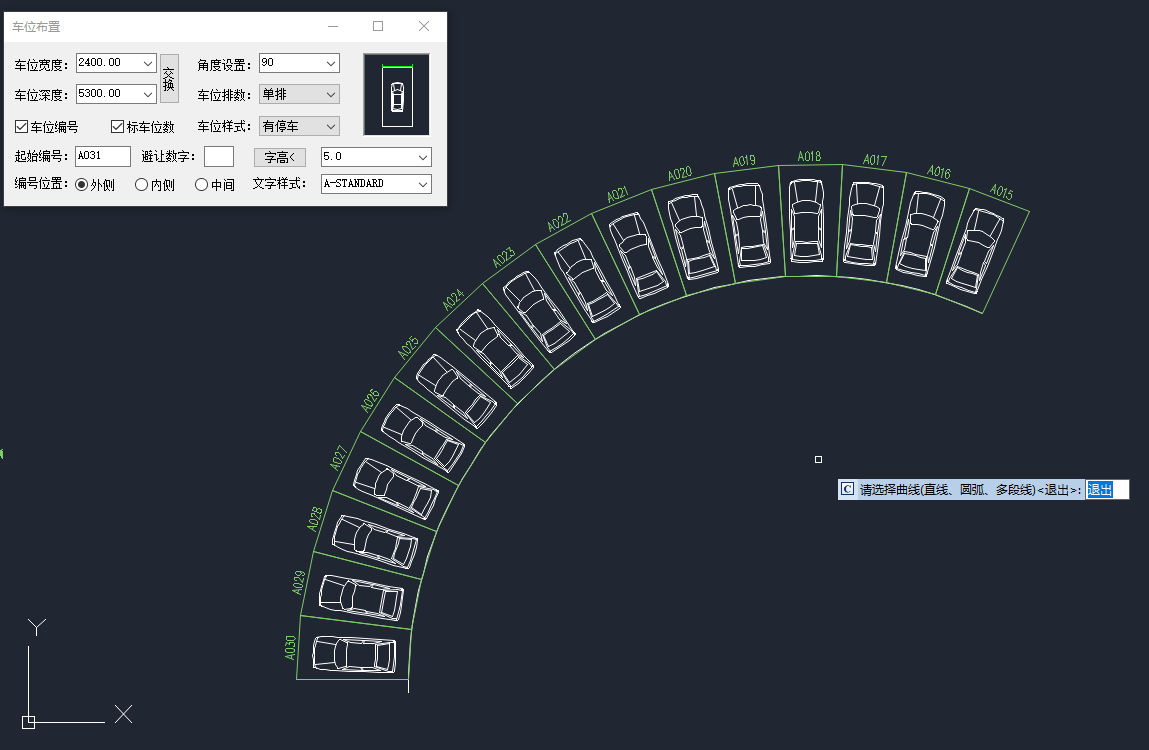
你还不会用CAD一键布置停车位？赶紧学起来！
在设计CAD建筑图的过程中，你还在一个一个地画停车位吗？那未免也太低效了吧！今天，小编用浩辰CAD建筑软件来教大家一键布置停车位，赶紧学起来吧！ 浩辰CAD建筑软件是行业应用最广泛的创新型建筑设计专业软件&…...
【MySQL之MySQL底层分析篇】系统学习MySQL，从应用SQL语法到底层知识讲解，这将是你见过最完成的知识体系
文章目录MySQL体系结构MySQL存储结构（以InnoDB为例）MySQL执行流程（以InnoDB为例）1. 数据写入原理2. 数据查询原理MySQL存储引擎1. 为什么需要不同的存储引擎2. 如何为数据指定不同的存储引擎，数据粒度又是多少3. MySQL…...
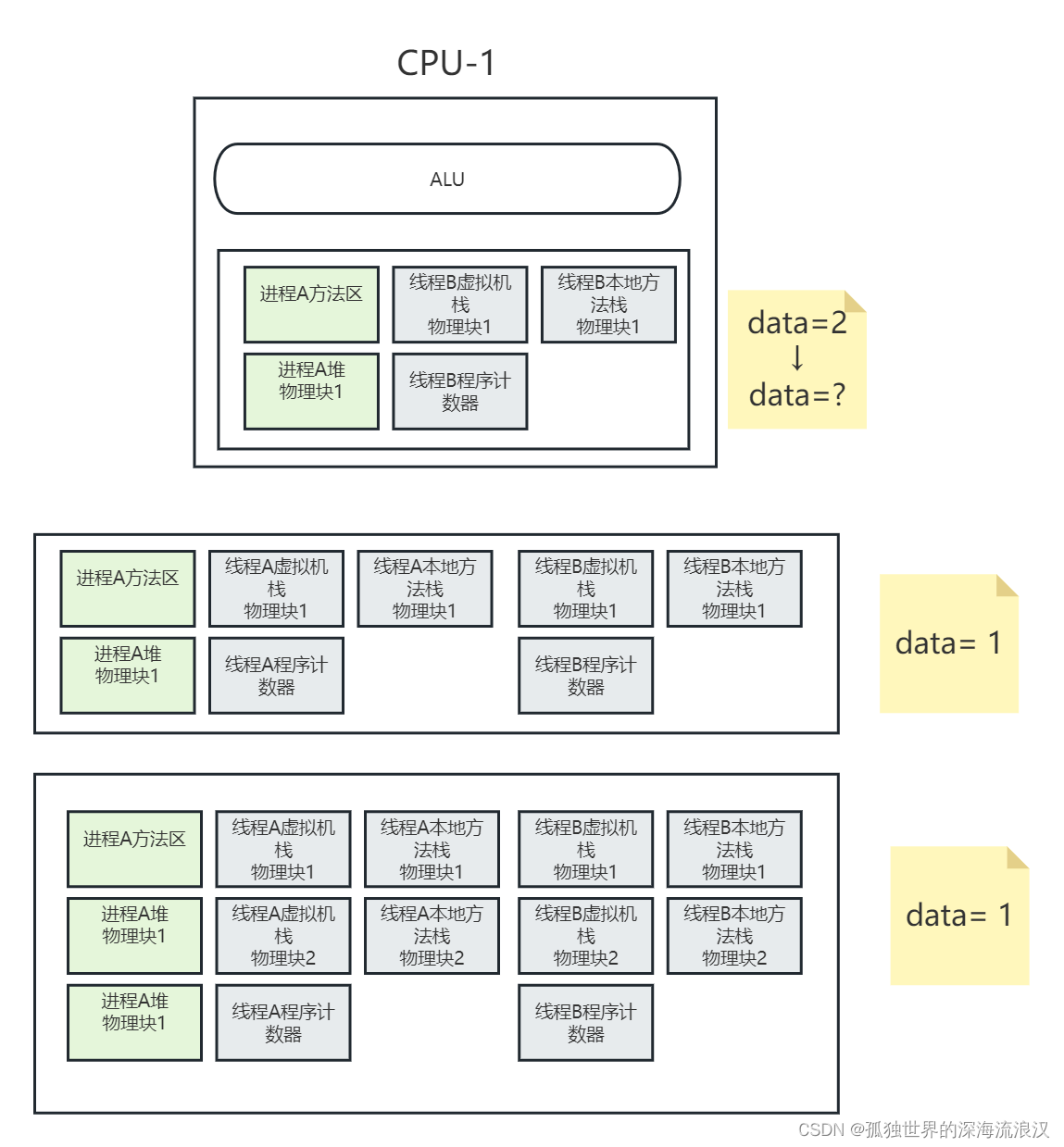
单核CPU是否有线程可见性问题？
本文仅是本人对问题的思考记录，并没有实操验证，有误请大家评论指出。 今天见到了一个经典的问题，单核CPU是否有线程可见性问题，学完操作系统应该可以直接回答，不会有线程安全问题。但如果结合JVM虚拟机来进行分析&…...
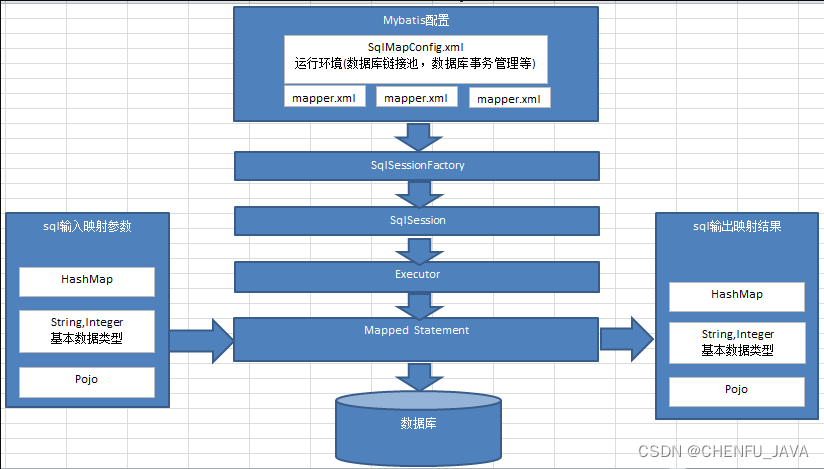
MyBatis 架构介绍
MyBatis 架构介绍MyBatis 架构图MyBatis 所解决的 JDBC 中存在的问题引用MyBatis 架构图 mybatis 配置:mybatis-config.xml，此文件作为 mybatis 的全局配置文件，配置了 mybatis 的运行环境等信息。另一个 mapper.xml 文件即 sql 映射文件，文件…...
基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统，利用大模型实现智能 UI 自动化，结合计算机视觉和自然语言处理技术，实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...
逻辑回归：给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告（肿瘤大小、血液指标），你需要做出一个**决定性判断**：恶性还是良性？这种“非黑即白”的抉择，正是**逻辑回归（Logistic Regression）** 的战场&a…...
练习（含atoi的模拟实现,自定义类型等练习）
一、结构体大小的计算及位段 （结构体大小计算及位段 详解请看：自定义类型：结构体进阶-CSDN博客） 1.在32位系统环境，编译选项为4字节对齐，那么sizeof(A)和sizeof(B)是多少？ #pragma pack(4)st…...
【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中，有几种方法可以执行Shell指令： 1. 使用system()函数 这是最简单的方法，包含在stdlib.h头文件中： #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...
《Playwright：微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络，将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具，支持 Chrome、Firefox、Safari 等主流浏览器，提供多语言 API（Python、JavaScript、Java、.NET）。它的特点包括&a…...
（二）TensorRT-LLM | 模型导出（v0.20.0rc3）
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述，后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作，其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...
EtherNet/IP转DeviceNet协议网关详解
一，设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络，本网关连接到EtherNet/IP总线中做为从站使用，连接到DeviceNet总线中做为从站使用。 在自动…...
【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计，提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合：各模块职责清晰，便于独立开发…...
中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学？传统医学奠基期（远古 - 17 世纪）近代医学转型期（17 世纪 - 19 世纪末）现代医学成熟期（20世纪至今） 中医的源远流长和一脉相承远古至…...
深入浅出深度学习基础：从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么？1.1.2 感知机的工作原理 1.2 感知机的简单应用：基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...