SDUT OJ《算法分析与设计》搜索算法
A - 子集和问题
Description
子集和问题的一个实例为〈S,t〉。其中,S={ x1 , x2 ,…,xn }是一个正整数的集合,c是一个正整数。子集和问题判定是否存在S的一个子集S1,使得:
![]()
。
试设计一个解子集和问题的回溯法。
对于给定的正整数的集合S={ x1 , x2 ,…,xn }和正整数c,计算S 的一个子集S1,使得:
![]()
。
Input
输入数据的第1 行有2 个正整数n 和c(n≤10000,c≤10000000),n 表示S 的大小,c是子集和的目标值。接下来的1 行中,有n个正整数,表示集合S中的元素。
Output
将子集和问题的解输出。当问题无解时,输出“No Solution!”。
Samples
Sample #1
Input
Output
5 10 2 2 6 5 4
2 2 6
#include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
int a[N];
int ans[N] = {0};
int n, c, sum;
bool flag = 0;
void print(int len){for(int i = 0; i < len; i++){if(i == len - 1){cout << ans[i] << "\n";}else{cout << ans[i] << ' ';}}
}
void Search(int x, int sum, int len){if(sum > c || flag) return ;if(sum == c){print(len);flag = 1;return ;}for(int i = x; i < n; i++){if(a[i] + sum <= c){ans[len] = a[i];Search(i+1, sum+a[i], len+1);}}
}
int main()
{sum = 0;cin >> n >> c;for(int i = 0; i < n; i++){cin >> a[i];sum += a[i];}if(sum < c){cout << "No Solution!" << "\n";}else{Search(0, 0, 0);if(!flag){cout << "No Solution!" << "\n";}}return 0;
}B - 运动员最佳匹配问题
Description
羽毛球队有男女运动员各n 人。给定2 个n×n 矩阵P 和Q。P[i][j]是男运动员i 和女运动员j配对组成混合双打的男运动员竞赛优势;Q[i][j]是女运动员i和男运动员j配合的女运动员竞赛优势。由于技术配合和心理状态等各种因素影响,P[i][j]不一定等于Q[j][i]。男运动员i和女运动员j配对组成混合双打的男女双方竞赛优势为P[i][j]*Q[j][i]。
设计一个算法,计算男女运动员最佳配对法,使各组男女双方竞赛优势的总和达到最大。
设计一个算法,对于给定的男女运动员竞赛优势,计算男女运动员最佳配对法,使各组男女双方竞赛优势的总和达到最大。
Input
输入数据的第一行有1 个正整数n (1≤n≤20)。接下来的2n 行,每行n个数。前n行是p,后n行是q。
Output
将计算出的男女双方竞赛优势的总和的最大值输出。
Samples
Sample #1
Input
Output
3 10 2 3 2 3 4 3 4 5 2 2 2 3 5 3 4 5 1
52
#include<bits/stdc++.h>
using namespace std;
const int N = 22;
int n, a[N][N], b[N][N], vis[N], pre[N], sum;
void dfs(int i, int cnt){if(i > n && cnt + pre[n] - pre[i-1] > sum){sum = max(sum, cnt);return ;}if(cnt + pre[n] - pre[i-1] > sum){for(int j = 1; j <= n; j++){if(vis[j] == 0){vis[j] = 1;dfs(i + 1, cnt + a[i][j] * b[j][i]);vis[j] = 0;}}}
}
int main()
{cin >> n;for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++){cin >> a[i][j];}}for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++){cin >> b[i][j];}}for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++){pre[i] = max(pre[i], a[i][j] * b[j][i]);}pre[i] += pre[i-1];}dfs(1, 0);cout << sum << "\n";return 0;
}C - 工作分配问题
Description
设有n件工作分配给n个人。将工作i分配给第j个人所需的费用为 cij。试设计一个算法,为每一个人都分配1 件不同的工作,并使总费用达到最小。
设计一个算法,对于给定的工作费用,计算最佳工作分配方案,使总费用达到最小。
Input
输入数据的第一行有1 个正整数n (1≤n≤11)。接下来的n行,每行n个数,表示工作费用。
Output
将计算出的最小总费用输出。
Samples
Sample #1
Input
Output
3 10 2 3 2 3 4 3 4 5
9
#include<bits/stdc++.h>
using namespace std;
const int N = 25;
const int INF = 0x3f3f3f3f;
int n, ans;
int a[N][N], vis[N];
void dfs(int i, int sum){if(sum > ans) return ;if(i == n + 1 && sum < ans){ans = sum;return ;}for(int j = 1; j <= n; j++){if(!vis[j]){vis[j] = 1;dfs(i + 1, sum + a[i][j]);vis[j] = 0;}}
}
int main()
{cin >> n;for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++){cin >> a[i][j];}}ans = INF;dfs(1, 0);cout << ans << "\n";return 0;
}D - 整数变换问题
Description
整数变换问题。关于整数i的变换f和g定义如下:f(i)=3i;
![]()
试设计一个算法,对于给定的2 个整数n和m,用最少的f和g变换次数将n变换为m。例如,可以将整数15用4 次变换将它变换为整数4:4=gfgg(15)。当整数n不可能变换为整数m时,算法应如何处理?
对任意给定的整数n和m,计算将整数n变换为整数m所需要的最少变换次数。
Input
输入数据的第一行有2 个正整数n和m。n≤100000,m≤1000000000。
Output
将计算出的最少变换次数以及相应的变换序列输出。第一行是最少变换次数。第2 行是相应的变换序列。
Samples
Sample #1
Input
Output
15 4
4 gfgg
#include<bits/stdc++.h>
using namespace std;
int maxn, n, m;
char f[101];
int search(int step, int sum){if(step > maxn) return 0;if(m == sum * 3 || search(step + 1, sum * 3)){f[step] = 'f';return 1;}if(sum / 2 == m || search(step+1, sum/2)){f[step] = 'g';return 1;}return 0;
}
int main()
{cin >> n >> m;maxn = 1;while(!search(1, n)){maxn ++;}cout << maxn << "\n";for(int i = maxn; i >= 1; i--){cout << f[i];}cout << "\n";return 0;
}相关文章:

SDUT OJ《算法分析与设计》搜索算法
A - 子集和问题 Description 子集和问题的一个实例为〈S,t〉。其中,S{ x1 , x2 ,…,xn }是一个正整数的集合,c是一个正整数。子集和问题判定是否存在S的一个子集S1,使得: 。 试设计一个解子…...
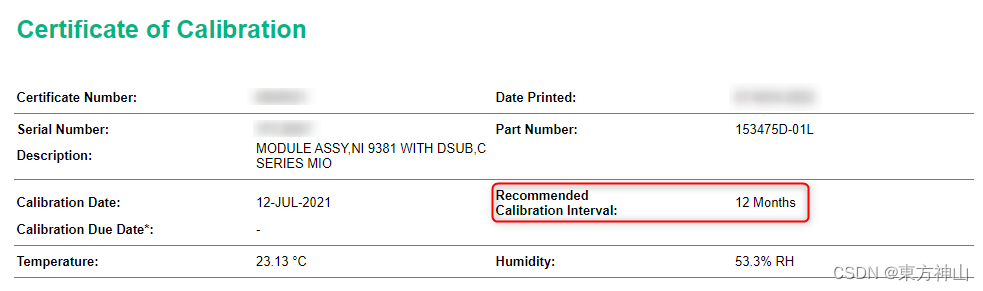
【NI-DAQmx入门】校准
1.设备定期校准的理由 随着时间的推移电子器件的特性会发生自然漂移,可能会导致测量结果的不准确性。防止出现良品和差品筛选出错的情况满足行业国际标准降低设备出现故障的风险使测量结果更具备参考性 2.查找NI设备的校准间隔。 定期校准会使DAQ设备的精度保持在…...

C语言链表
head.h typedef struct Node_s{int data; //数据域struct Node_s *pNext; //指针域 } Node_t, *pNode_t;void headInsert(pNode_t *ppHead, pNode_t *ppTail, int data); void print(pNode_t pHead); void tailInsert(pNode_t *ppHead, pNode_t *ppTail, int data); void sort…...
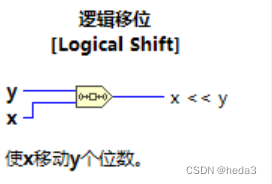
LabVIEW进行MQTT通信及数据解析
需求:一般通过串口的方式进行数据的解析,但有时候硬件的限制,没法预留串口,那么如何通过网络的方式特别是MQTT数据的通信及解析 解决方式: 1.MQTT通信控件: 参考开源的mqtt-LabVIEW https://github.com…...

基于DOTween插件实现金币飞行到指定位置功能
文章目录 前言一、DOTween是什么?二、使用步骤1.导入DOTween插件在Unity官方插件商店找到DOTween插件导入DOTween插件启用DOTween插件 2.代码逻辑金币飞行代码控制飞行效果代码 3.物体配置1.物体上装配CoinEffect脚本2.在金币预制体上装配FlyControl脚本 三、效果展…...

python-opencv 培训课程作业
python-opencv 培训课程作业 作业一: 第一步:读取 res 下面的 flower.jpg,读取彩图,并用 opencv 展示 第二步:彩图 -> 灰度图 第三步:反转图像:最大图像灰度值减去原图像,即可得…...

【Go入门】并发
【Go入门】并发 有人把Go比作21世纪的C语言,第一是因为Go语言设计简单,第二,21世纪最重要的就是并行程序设计,而Go从语言层面就支持了并行。 goroutine goroutine是Go并行设计的核心。goroutine说到底其实就是协程,…...
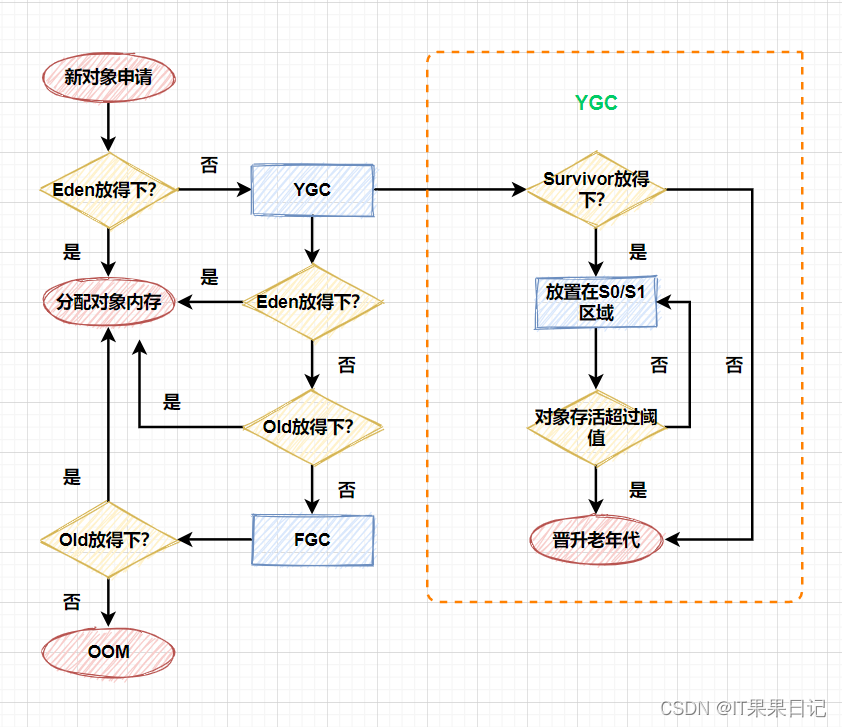
Java虚拟机运行时数据区结构详解
Java虚拟机运行时数据区结构如图所示 程序计数器 程序计数器(Program Counter Register)是一块较小的内存空间,它可以看作是当前线程所执行的字节码的行号指示器。 多线程切换时,为了能恢复到正确的执行位置,每条线程…...
)
华为OD机试 - 转盘寿司(Java JS Python C)
目录 题目描述 输入描述 输出描述 用例 题目解析 JS算法源码 Java算法源码...

【ATTCK】MITRE Caldera-emu插件
CALDERA是一个由python语言编写的红蓝对抗工具(攻击模拟工具)。它是MITRE公司发起的一个研究项目,该工具的攻击流程是建立在ATT&CK攻击行为模型和知识库之上的,能够较真实地APT攻击行为模式。 通过CALDERA工具,安全…...
23111709[含文档+PPT+源码等]计算机毕业设计基于Spring Boot智能无人仓库管理-进销存储
文章目录 **软件开发环境及开发工具:****功能介绍:****论文截图:****数据库:****实现:****代码片段:** 编程技术交流、源码分享、模板分享、网课教程 🐧裙:776871563 软件开发环境及…...

SDUT OJ《算法分析与设计》贪心算法
A - 汽车加油问题 Description 一辆汽车加满油后可行驶n公里。旅途中有若干个加油站。设计一个有效算法,指出应在哪些加油站停靠加油,使沿途加油次数最少。并证明算法能产生一个最优解。 对于给定的n和k个加油站位置,计算最少加油次数。 I…...
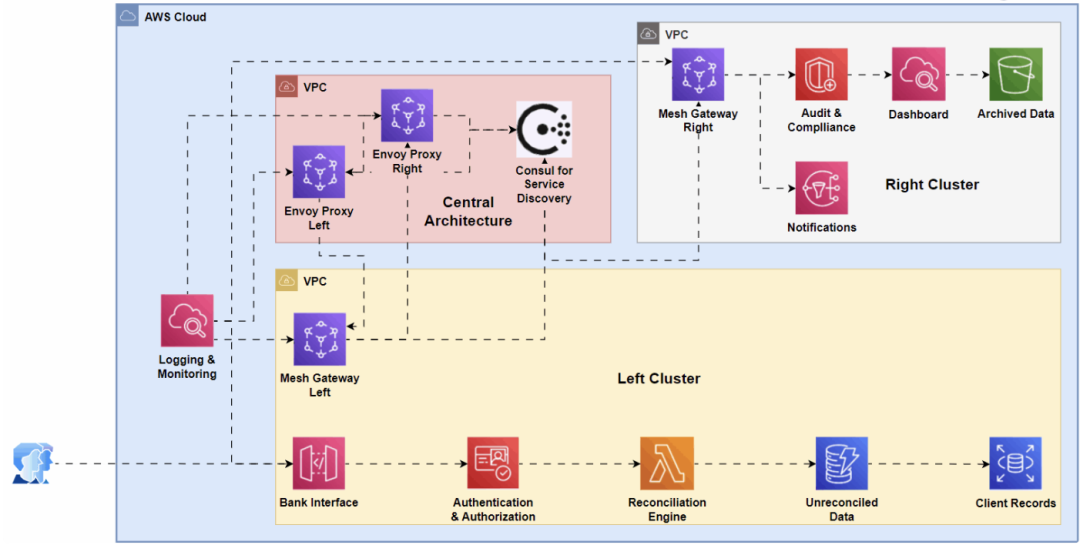
金融业务系统: Service Mesh用于安全微服务集成
随着云计算的不断演进,微服务架构变得日益复杂。为了有效地管理这种复杂性,人们开始采用服务网格。在本文中,我们将解释什么是Service Mesh,为什么它对现代云架构至关重要,以及它是如何解决开发人员今天面临的一些最紧…...

Linux下快速确定目标服务器支持哪些协议和密码套件
实现原理是利用TLS协议的特点和握手过程来进行测试和解析响应来确定目标服务器支持哪些TLS协议和密码套件。 在TLS握手过程中,客户端和服务器会协商并使用相同的TLS协议版本和密码套件来进行通信。通过发送特定的握手请求并分析响应,可以确定目标服务器…...

LeetCode100122. Separate Black and White Balls
文章目录 一、题目二、题解 一、题目 There are n balls on a table, each ball has a color black or white. You are given a 0-indexed binary string s of length n, where 1 and 0 represent black and white balls, respectively. In each step, you can choose two a…...
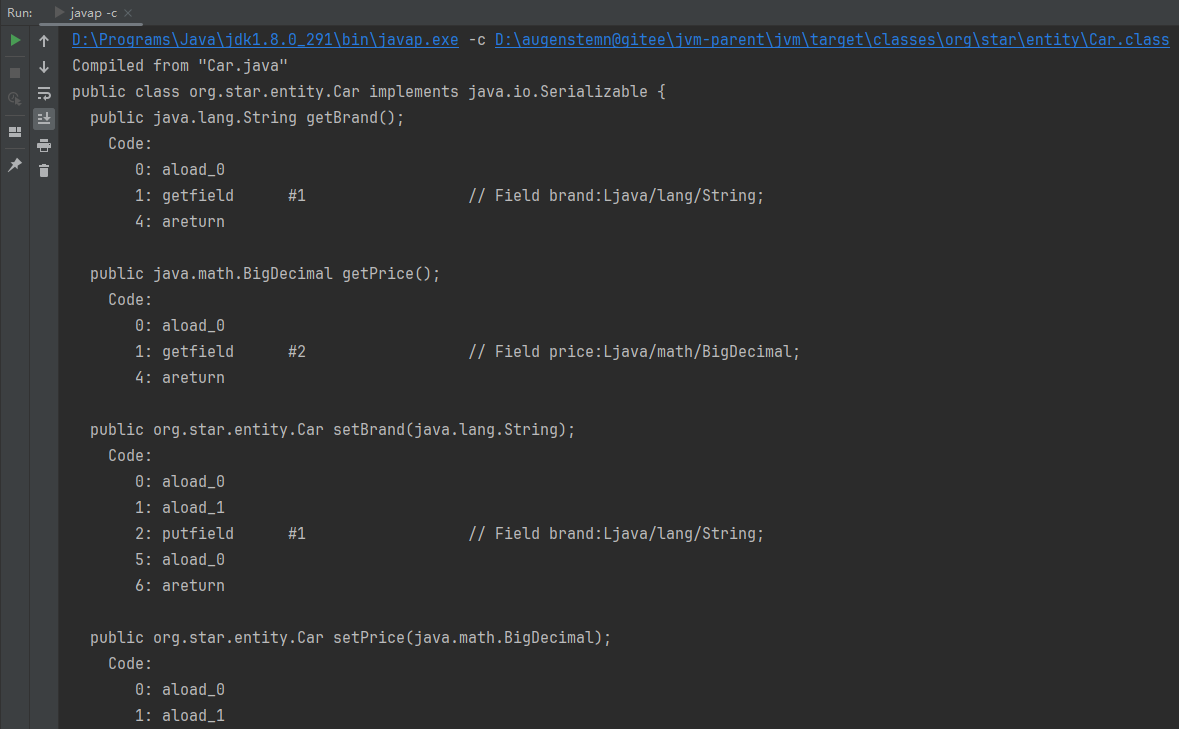
系列二十六、idea安装javap -c
一、概述 javap -c是一个能够将.java文件反编译为.class文件的指令,例如我在idea中编写了一个Car.java文件,我想看看这个类被编译后长什么样的,就可以使用该指令进行查看。 二、配置 2.1、 Java Bytecode Decompiler File>Settings>Pl…...

nginx 如何根据IP做限流,以及 nginx 直接返回 json 格式数据
Nginx 限流配置 Nginx是如何限流的。随着业务的扩散,系统并发越来越高时,有三样利器用来保护系统,分别是缓存、降级和限流。 随着业务的扩散,系统并发越来越高时,有三样利器用来保护系统,分别是缓存、降…...

C语言链式栈
stack.h typedef struct Node_s {int data;struct Node_s *pNext; } Node_t, *pNode_t;typedef struct Stack_s {pNode_t pHead;//栈顶指针,指向了链表的第一个结点int size;//栈的元素个数 } Stack_t, *pStack_t;void init(pStack_t pStack); void push(pStack_t …...

【Go入门】 Go的http包详解
【Go入门】 Go的http包详解 前面小节介绍了Go怎么样实现了Web工作模式的一个流程,这一小节,我们将详细地解剖一下http包,看它到底是怎样实现整个过程的。 Go的http有两个核心功能:Conn、ServeMux Conn的goroutine 与我们一般编…...
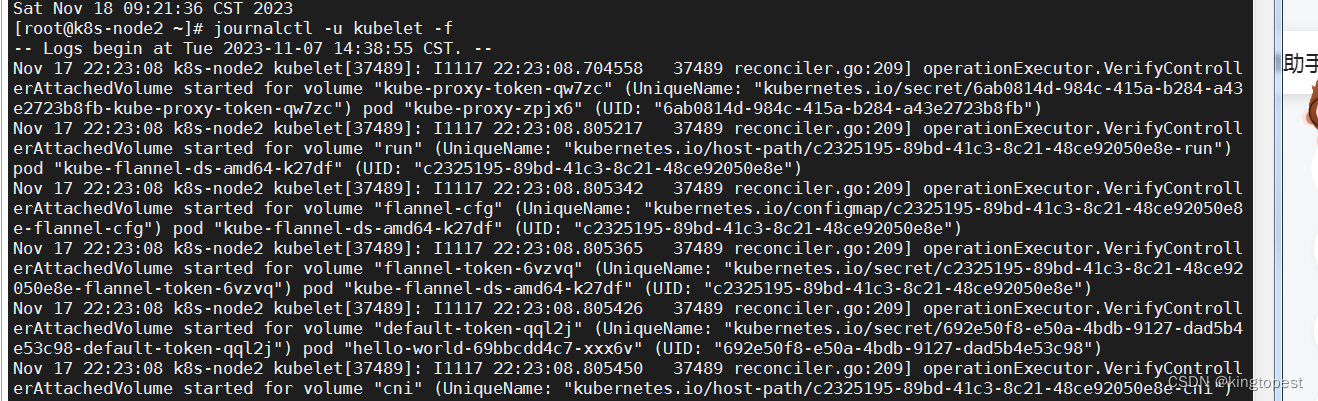
解决k8s node节点报错: Failed to watch *v1.Secret: unknown
现象: 这个现象是发生在k8s集群证书过期,重新续签证书以后。 记得master节点的/etc/kubernetes/kubelet.conf文件已经复制到node节点了。 但是为什么还是报这个错,然后运行证书检查命令看一下: 看样子是差/etc/kubernetes/pki/…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...
:处理原始数据命令)
ffmpeg(三):处理原始数据命令
FFmpeg 可以直接处理原始音频和视频数据(Raw PCM、YUV 等),常见场景包括: 将原始 YUV 图像编码为 H.264 视频将 PCM 音频编码为 AAC 或 MP3对原始音视频数据进行封装(如封装为 MP4、TS) 处理原始 YUV 视频…...

免费批量Markdown转Word工具
免费批量Markdown转Word工具 一款简单易用的批量Markdown文档转换工具,支持将多个Markdown文件一键转换为Word文档。完全免费,无需安装,解压即用! 官方网站 访问官方展示页面了解更多信息:http://mutou888.com/pro…...

Vue.js教学第二十一章:vue实战项目二,个人博客搭建
基于 Vue 的个人博客网站搭建 摘要: 随着前端技术的不断发展,Vue 作为一种轻量级、高效的前端框架,为个人博客网站的搭建提供了极大的便利。本文详细介绍了基于 Vue 搭建个人博客网站的全过程,包括项目背景、技术选型、项目架构设计、功能模块实现、性能优化与测试等方面。…...
